1009-报废

废了。

T1-很工业。

初

考试推出了正确的柿子。打了令人感动的高精。

末

××我高精加减乘写跪了。

怕是废了。

#include <iostream>
#include <cstring>
#include <cstdio>
#define N 322
#define Bit 555
//#define LL long long
//容斥……高精度？？？
//double丢位丢的真严重啊……
using namespace std;
struct Hyper_long{
	int A[Bit];
	Hyper_long(){}
	int length(){
		return A[0];
	}
	void out(){
		printf("%d",A[A[0]]);
		for(int i=A[0]-1;i>=1;i--)
			printf("%04d",A[i]);
		puts("");
	}
	friend Hyper_long operator + (Hyper_long &a,Hyper_long &b){
		Hyper_long c;
		long long uped=0,len=max(a.length(),b.length())+1;
		for(int i=1;i<=len;i++){
			c.A[i]=a.A[i]+b.A[i]+uped;
			uped=c.A[i]/10000;
			c.A[i]%=10000;
		}
		c.A[0]=len;
		while(c.A[c.A[0]]==0&&c.A[0]>1)c.A[0]--;
		return c;
	}
};
int len;
Hyper_long C[N][N],ans1,ans2,dat,_1;
void operator -= (Hyper_long &a,Hyper_long &b){
	for(int i=1;i<=a.length();i++){
		a.A[i]-=b.A[i];
		if(a.A[i]<0){
			a.A[i]+=10000;
			a.A[i+1]--;
		}
	}
	int len=a.length();
	while(len>1&&a.A[len]==0)len--;
	a.A[0]=len;
}
void operator *= (Hyper_long &a,int num){
	long long uped=0;
	for(int i=1;i<=a.length();i++){
		a.A[i]=a.A[i]*num+uped;
		uped=a.A[i]/10000;
		a.A[i]%=10000;
	}
	while(uped!=0){
		a.A[0]++;
		a.A[a.A[0]]=uped;
		uped=a.A[a.A[0]]/10000;
		a.A[a.A[0]]%=10000;
	}
}
int main(){
//	freopen("1.in" ,"r",stdin);\
	freopen("1.out","w",stdout);
	_1.A[0]=1;
	_1.A[1]=1;
	for(int i=0;i<=200;i++){
		C[i][0]=_1;C[i][i]=_1;
		for(int j=1;j<i;j++){
			C[i][j]=C[i-1][j]+C[i-1][j-1];
		}
	}
	scanf("%d",&len);
	for(int i=1;i<=len;i++)
		for(int j=1;j<=len;j++)
			scanf("%*d");
	for(int i=0;i<=len;i++){
		dat=C[len][i];
		for(int j=1;j<=len-i;j++)
			dat*=j;
		if(i&1) ans1=ans1+dat;//ans1.out();
		else    ans2=ans2+dat;//ans2.out();
	}
	//ans1.out();
	//ans2.out();
	ans2-=ans1;
	ans2.out();
}

T2

由于竞赛图的特殊性质。

把$P$图的边分别正向和反向连入$Q$图，然后判断是否为$DAG$。

复杂度是$\Theta(N^2)$的。

为什么这样是正确的呢……

感性理解，$Q$图$P$图中没有公共的直接连接的节点。

我们把$Q$图全部正着加入$P$图，并判断是否为$DAG$。

因为在竞赛图里，所以图不会不联通，于是只要判环

这时如果有环，一定不联通。（但是很移动）

这个环有两种情况：

1. 在一个图里，这样图一定不连通。
2. 在两个图的边界（即共有的），这样因为每个图只有半个环即一条链，一定不连通。

如图：

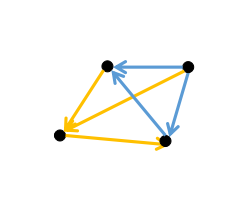
那么就结束了么？不。

看这个：

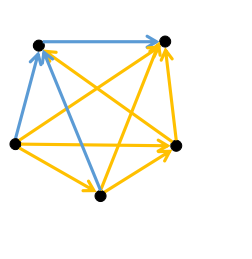
它是$DAG$但是两个图都不连通。

但是可以发现，如果两个不连通的图构成了$DAG$，那么把一个图全部翻转（$f$到$t$变成$t$到$f$）后，一定会出环。

所以反加边再查一遍。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#define N 4096

using namespace std;
struct Myqueue{
	int A[N<<2],f,b;
	Myqueue(){f=b=0;}
	void clear(){f=b=0;}
	int front(){return A[f];}
	void push(const int k){A[b++]=k;}
	void pop(){f++;}
	bool empty(){return f==b;}
	void pour(){
		if(empty())puts("Empty");
		else{
			for(int i=f;i<b;i++){
				printf("%d ",A[i]);
			}
			puts("");
		}
	}
}q;
char st[N];
bool mp[N][N];
int deg[N],dat[N],pn;
vector<pair<int,int> >pv;

bool check(){
	for(int i=1;i<=pn;i++)
		dat[i]=deg[i];//cout<<deg[i]<<" ";
//	puts("");
	for(int i=1;i<=pn;i++)
		if(dat[i]==0)
			q.push(i);
	while(!q.empty()){
//		q.pour();
		int f=q.front();q.pop();
//		cout<<"F:"<<f<<endl;
		for(int t=1;t<=pn;t++){
			if(mp[f][t]){
				dat[t]--;
				if(dat[t]==0)
					q.push(t);
			}
		}
	}
	for(int i=1;i<=pn;i++)
		if(dat[i]!=0)return 0;
	return 1;
}
void prerun(){
	pv.clear();
	memset(mp ,0,sizeof mp);
	memset(deg,0,sizeof deg);
}
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		prerun();
		scanf("%d",&pn);
		for(int i=1;i<=pn;i++){
			scanf("%s",st+1);
			for(int j=1;j<=pn;j++){
				if(st[j]=='P'){
					mp[i][j]=1;
					deg[j]++;
//					puts("adsuhiohcakjn");
				}
				else if(st[j]=='Q')
					pv.push_back(make_pair(i,j));
			}
		}
		bool is_ok=1;
		for(int i=0;i<pv.size();i++){
			mp[pv[i].first][pv[i].second]=1;
			deg[pv[i].second]++;
		}
		is_ok=is_ok&check();
		for(int i=0;i<pv.size();i++){
			mp[pv[i].first ][pv[i].second]=0;
			mp[pv[i].second][pv[i].first ]=1;
			deg[pv[i].second]--;
			deg[pv[i].first]++;
		}
		is_ok=is_ok&check();
		printf("%s\n",is_ok?"T":"N");
	}
}

T3

数位$DP$(神仙题)

上面有0.1号字写的题解呢……