经典dp练习
在这里尝试记录一下各种比较不错可做的dp复习和练习记录。(这里只会写大概的思路和抽象的代码。）
最长上升子序列
给一个长度为 \(N\) 的数列，求数值严格单调递增的子序列的长度最长是多少。
- 直接暴力枚举从哪里转移过来的 \(O(N^2)\)。
rep(i, 1, n+1) rep(j, 1, i) if (a[i] > a[j]) setmax(dp[i], dp[j]+1);
cout << *max_element(all(dp)) << '\n';
- 可以发现对于所有的 \(j < i,\ a_i>a_j,\ dp_i=max(dp_j)\)，所以这里直接离散化 + 权值树状数组，每次按顺序查询小于 \(dp_i\) 的最大 \(dp_j\)。当然注意这里如果是严格大于的话离散化不能有重复值 \(O(NlogN)\)。
auto a = gen_dvec(a); // 离散化
rep(i, 1, n+1) {
setmax(dp[i], bit.prefix(a[i]-1)+1);
bit.modify(a[i], dp[i]);
}
Brackets(POJ2955)
给一个括号序列包含\(()[]\)，求匹配数。
\(S_l=S_r\ ?\ dp_{l,r}=dp_{l-1,r-1}+2\ :\ dp_{l+1,r}\) / \(O(N^3)\)
// recursive
int solve(int l, int r) {
if (l > r) return 0;
if (dp[l][r] != -1) return dp[l][r];
rep(mid, l+1, r+1) {
if (can_pair(s[l], s[mid])) setmax(dp[l][r], solve(l+1, mid-1) + solve(mid+1, r) + 2);
else setmax(dp[l][r], solve(l+1, r));
}
return dp[l][r] != -1 ? dp[l][r] : solve(l+1, r);
}
// iterative
for (int len = 2;len <= n;len ++) {
for (int l = 1; l + len - 1 <= n; l ++) {
int r = l + len - 1;
if (can_pair(s[l], s[r]))
dp[l][r] = max(dp[l][r], dp[l + 1][r - 1] + 2);
for (int k = l + 1; k < r; k ++)
dp[l][r] = max(dp[l][r], dp[l][k] + dp[k][r]);
}
}
整数划分
现在给定一个正整数 \(N\)，请求出 \(N\) 共有多少种不同的划分方法 (eg: 4 = 1+1+1+1 = 1+1+2 = 2+2)。
完全背包板子 \(O(N^2logN)\)，体积比较特殊可以优化成 \(O(N^2)\)。
dp[0][0] = 1;
rep(i, 1, n+1) rep(j, 0, n+1) for (int k = 0; j >= k*i; ++j) dp[i][j] += dp[i-1][j - k*i];
cout << dp[n][n] << '\n';
最长回文字串
输入一个字符串 \(str\) , 输出 \(str\) 里最长回文子串的长度。
最长回文子序列 = 最长公共子序列
这个题有 \(O(N^3) /O(N^2logN)/O(N^2)/O(NlogN)/O(N)\) 的做法，这里只说 \(O(N^2)\) 的做法，\(dp_{i,j}\) 代表 \(str_i \to str_j\) 是不是回文串，那么 \(dp_{i,j} = (dp_{i-1,j-1}\ \&\&\ s_i==s_j)\)，要注意区分奇偶。
vector<vector<bool>> f(n+1, vector<bool>(n+1));
rep(i, 0, n+1) { f[i][i] = 1; if (i+1 <= n) f[i][i+1] = f[i+1][i] = s[i] == s[i+1]; }
int ans = 1;
for (int len = 2; len <= n; ++len) {
rep(l, 1, n) {
int r = l + len - 1;
if (r > n) break;
if (s[l] == s[r]) f[l][r] = f[l+1][r-1];
if (f[l][r]) setmax(ans, r - l + 1);
}
}
田忌赛马(POJ2287)
题面比较长，大概意思就是说你和齐王都有 \(N\) 匹马，你俩每次对着出马，如果赢了加1分输了减1分，平了不加不减。齐王每次从大到小出马，你要合理安排出马顺序使得收益最大。
牛逼题，首先如果不考虑平局可以直接贪心，如果能赢直接赢，如果输了就输最弱的那匹马(题面说的二分图最大匹配也可以但是没必要)。但是如果考虑平局的就不能这么做，来个智慧样例：
1 2 3 --- 1 2 3
2 3 --- 1 3
这时候其实也可以跑最小费用最大流，很显然我现在还不会。。要分析出来我每次出在区间 \([i,j]\) 的马中只会出第 \(i\) 只或第 \(j\) 只，也就是要不然就以最大的和你平手，要不然就出最小的输掉，出其他的马不会变的更优，所以可以考虑区间dp。不过我看到有人是贪心过去的，暂时还没想到怎么做。
VI a(n+1); rep(i, 1, n+1) cin >> a[i]; sort(all(a));
VI b(n+1); rep(i, 1, n+1) cin >> b[i]; sort(all(b));
vector<VI> dp(n+1, VI(n+1, -(int) 1e9));
rep(i, 1, n+1) dp[i][i] = (a[i] > b[1] ? 200 : a[i] == b[1] ? 0 : -200);
rep(len, 2, n+1) rep(l, 1, n+1) {
int r = l + len - 1;
if (r > n) break;
// [l+1, r] / [l, r-1]
int c1 = (a[l] > b[len] ? 200 : a[l] == b[len] ? 0 : -200);
int c2 = (a[r] > b[len] ? 200 : a[r] == b[len] ? 0 : -200);
setmax(dp[l][r], dp[l+1][r] + c1);
setmax(dp[l][r], dp[l][r-1] + c2);
}
cout << dp[1][n] << '\n';
花店橱窗(Nowcoder1005)
\(n\) 个花 \(m\) 个花瓶，每个花插到花瓶里都有一个对应的观赏值，再不能改变花的相对顺序前提下，最大化观赏值总和并输出最小字典序。
数据范围 \(n,m\leq 100\)，比较小可以乱搞，\(dp_{i,j}\) 为第 \(i\) 个花插到第 \(j\) 个花瓶的最大观赏值，\(dp_{i,j}=max(dp_{i-1,i-1\sim j-1})\)，答案就是 \(max(dp_{n,n\sim m})\)，输出路径的话就记一下从哪里转移过来的就行，字典序最小就是把判断条件改成严格大于，相反字典序最大就改成大于等于。
rep(i, 1, n+1) rep(j, 1, m+1) cin >> v[i][j];
rep(j, 1, m-n+2) dp[1][j] = v[1][j];
vector<VP> pre(101, VP(101));
rep(i, 2, n+1) rep(j, i, m - (n - i)+1) rep(k, i-1, j) if (setmax(dp[i][j], dp[i-1][k] + v[i][j])) pre[i][j] = {i-1, k};
int ans = -2e9;
PI cur = {};
rep(j, n, m+1) if (setmax(ans, dp[n][j])) cur = {n, j};
cout << ans << '\n';
VI p;
while (cur != make_pair(0, 0)) {
p.pb(cur.se);
cur = pre[cur.fi][cur.se];
}
per(i, n, 0) cout << p[i] << " \n"[i == 0];
邮票面值设计(NOIP1999 提高组)
给定一个信封，最多只允许粘贴 \(N\) 张邮票，计算在给定 \(K(N+K \leq 15)\) 种邮票的情况下（假定所有的邮票数量都足够），如何设计邮票的面值，能得到最大值 \(MAX\) ，使在 \(1\) 到 之间的每一个邮资值都能得到。
数据量比较小可以去暴搜。首先需要确定每个数枚举的范围， 设第 \(i\) 个数选的是 \(x\)，那么第 \(i+1\) 个数选择的范围必定是在 \([x+1,x\times i+1]\) ，直接枚举就行，但是这里需要检查当前的选择是否满足 \(1\) 到 \(MAX\) 之间的每一个邮资值都能得到，裸的完全背包， \(dp_j\) 代表前 \(i\) 个数中凑成体积恰好为 \(j\) 的最少个数，每次就check一下 \(dp_{1\sim MAX}\leq inf\) 就行了
public class Main {
static int[] path = new int[20], temp = new int[20];
static int n, k, ans;
static int solve(int u, int m) {
m *= n;
int[] dp = new int [m + 1];
for (int i = 0; i <= m; i++)
dp[i] = (int) 1e9;
dp[0] = 0;
for (int i = 1; i <= u; i++)
for (int j = temp[i]; j <= m; j++)
if (dp[j - temp[i]] + 1 <= n)
dp[j] = Math.min(dp[j], dp[j - temp[i]] + 1);
for (int i = 0; i <= m; i++)
if (dp[i] == (int) 1e9)
return i - 1;
return m;
}
static void dfs(int u, int lst, int max_val) {
if (u == k + 1) {
if (max_val > ans) {
ans = max_val;
for (int i = 1; i <= k; i++)
path[i] = temp[i];
}
return;
}
for (int i = lst + 1; i <= max_val + 1; i++) {
temp[u] = i;
int res = solve(u, i);
if (res > max_val) dfs(u + 1, i, res);
}
}
public static void main(String[] args) throws Exception {
n = nextInt();
k = nextInt();
dfs(1, 0, 0);
for (int i = 1; i <= k; i++)
cout.print(path[i] + " ");
cout.println();
cout.println("MAX=" + ans);
closeAll();
}
}
我不是大富翁 (Nowcoder)
https://ac.nowcoder.com/acm/contest/75771/D
https://codeforces.com/contest/1941/problem/D (一样的题)
\(N\) 个人围城一圈传 \(M\) 次球， 每次可以自己选择顺时针或者逆时针传 \(a_i\) 个人，在游戏的开始时处于 \(1\) 号地块，是否存在这样一种移动方式，使得 $m $ 个回合后他依旧在 \(1\) 号地块。
\(dp_{i,j}\) 代表过了前 \(i\) 轮 现在是否有可能在第 \(j\) 个人手上，这里有个小技巧需要把 \(1\to n\) 映射成 \(0 \to n-1\)，这样方便符合题目要求取模，那么可以按两个方向来的进行 dp
int n, m; cin >> n >> m;
VI a(m+1);
int tot = 0;
rep(i, 1, m+1) {
cin >> a[i];
}
vector<VI> dp(m+1, VI(n));
dp[0][0] = 1;
rep(i, 1, m+1) rep(j, 0, n) {
int lst = (j + a[i]) % n;
setmax(dp[i][j], dp[i-1][lst]);
lst = ((j - a[i]) % n + n) % n;
setmax(dp[i][j], dp[i-1][lst]);
}
E. Rudolf and k Bridges
https://codeforces.com/contest/1941/problem/E
Bernard loves visiting Rudolf, but he is always running late. The problem is that Bernard has to cross the river on a ferry. Rudolf decided to help his friend solve this problem.
The river is a grid of \(n\) rows and \(m\) columns. The intersection of the \(i\)-th row and the \(j\)-th column contains the number \(a_{i,j}\) — the depth in the corresponding cell. All cells in the first and last columns correspond to the river banks, so the depth for them is \(0\).
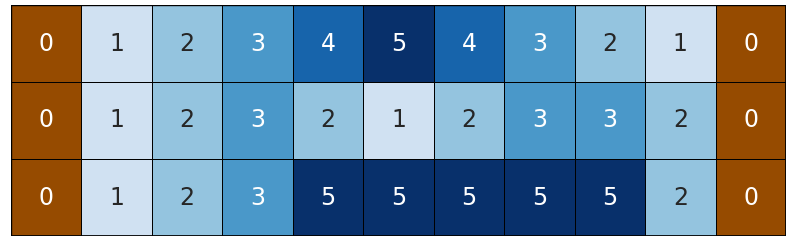The river may look like this.
Rudolf can choose the row \((i,1), (i,2), \ldots, (i,m)\) and build a bridge over it. In each cell of the row, he can install a support for the bridge. The cost of installing a support in the cell \((i,j)\) is \(a_{i,j}+1\). Supports must be installed so that the following conditions are met:
- A support must be installed in cell \((i,1)\);
- A support must be installed in cell \((i,m)\);
- The distance between any pair of adjacent supports must be no more than \(d\). The distance between supports \((i, j_1)\) and \((i, j_2)\) is \(|j_1 - j_2| - 1\).
Building just one bridge is boring. Therefore, Rudolf decided to build \(k\) bridges on consecutive rows of the river, that is, to choose some \(i\) (\(1 \le i \le n - k + 1\)) and independently build a bridge on each of the rows \(i, i + 1, \ldots, i + k - 1\). Help Rudolf minimize the total cost of installing supports.
首先因为每一排独立的，所以每一排进行单独dp就可以。\(dp_i\) 代表在前 \(i\) 个数中选并且第 \(i\) 个数必选的间隔不超过 \(d\) 的最小花费，很容易得到一个 \(O(m^2)\) 的式子:
rep(i,1,m+1) rep(j, max(1, i - d - 1), i) setmin(dp[i], dp[j] + g[r][i]);
很容易发现可以用一个经典trick就是开一个线段树然后每次查 \(min(dp_{i-d-1\to i})\) 来更新 \(dp_i\) 就好了，复杂度可以优化成 \(O(mlogm)\)。
更进一步，这样的题目可以直接用单调队列优化成 \(O(m)\) 的。对于一个 \(i>j\)，如果 \(dp_i<dp_j\)，那么 \(dp_j\) 对我来说不会有任何用处，因为我在更新后面的点的最优值的时候一定会选择 \(dp_i\) 来更新，于是我就可以开一个队列然后每次只将未来可能成为'转移基点'的点入队，这样每个元素只会入队一次出队一次。
int n, m, k, d; cin >> n >> m >> k >> d;
vector<vector<ll>> g(n+1, vector<ll>(m+1));
rep(i,1,n+1) rep(j,1,m+1) cin >> g[i][j], g[i][j]++;
vector<ll> cost{0};
rep(r,1,n+1) {
vector<ll> dp(m+1, inf);
dp[1] = 1;
deque<pair<ll, int>> q;
q.push_back(make_pair(dp[1], 1));
rep(i,1,m+1) {
while (!q.empty() && i - q.front().se - 1 > d) q.pop_front();
setmin(dp[i], q.front().fi + g[r][i]);
while (!q.empty() && dp[i] < q.back().fi) q.pop_back();
q.push_back(make_pair(dp[i], i));
}
cost.pb(dp[m]);
}
rep(i,1,n+1) cost[i] += cost[i-1];
ll ans = inf;
rep(i,1,n+1) {
if (i + k - 1 > n) break;
setmin(ans, cost[i + k - 1] - cost[i - 1]);
}
cout << ans << '\n';
浙公网安备 33010602011771号