P1117 [NOI2016] 优秀的拆分 题解

据说暴力用哈希扫可以拿到95分。

这一道题的思路是这个样子的：

我们首先准备两个数组a[]和b[]，分别表示以 \(i\) 结尾的形似AA的字串个数和以 \(i\) 开头的形似AA的字串的个数，最终答案其实就是 \(\displaystyle \sum_{i=1}^n a[i] \times b[i+1]\)。

然后考虑如何求出这两个数组。

对于每一个位置，我们尝试枚举一个 \(len\)，然后求出当前位置 \(i\) 与 \(i+len\) 位置处的 lcp 与 lcs 。

当两者长度加起来不小于 \(len\) 的时候，就意味着我们可以找到至少一个长度为 \(2len\) 的AA串。

为什么呢？

我们考虑从两个位置的 lcs 的开头处开始，分别向后截取出一段长度为 \(len\) 的串。

如果这个串被两者的 lcs 和两者的 lcp 拼起来组成的一个字串覆盖，那么我们就可以把这两个串拼起来，形成一个长度为 \(2len\) 的AA串。
就像这样：

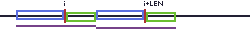
当两者长度加起来不够 \(len\) 时，我们截出来的两端字串就不保证一样。
不，应该是保证不一样，要不然两者的 lcp 还可以更长一点。
这样就拼不出来一个长度为 \(2len\) 的AA串了。

如果两者甚至有重合，那么我们就可以挑出来多个字串。我们这些会累积到后面。

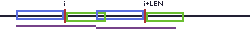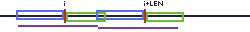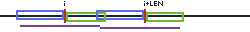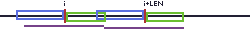
就是这样。

简单来说，我们需要做的就是：

1. 枚举 \(len\)；这个操作的复杂度是 \(O(n \log n)\)
2. 求 lcp 与 lcs；使用后缀数组即可。
3. 区间加；差分即可。

上代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1001000;
int T;
ll a[N], b[N];
struct SuffixArray
{
	char S[N]; int n;
	int cnt[N], sa[N], rk[N], height[N];
	int st[N][25], lg2[N];
	struct node
	{
		int id, x, y;
	}aa[N], bb[N];

	inline void buildsa()
	{
		n = strlen(S + 1);
		memset(cnt, 0, sizeof(cnt));
		memset(height, 0, sizeof(height));
		memset(sa, 0, sizeof(sa));
		memset(rk, 0, sizeof(rk));
		for(int i = 1; i <= n; i++) aa[i] = bb[i] = { 0,0,0 };
		for(int i = 1; i <= n; i++) cnt[S[i]] = 1;
		for(int i = 1; i <= 256; i++) cnt[i] += cnt[i - 1];
		for(int i = 1; i <= n; i++) rk[i] = cnt[S[i]];
		for(int L = 1; L < n; L *= 2)
		{
			for(int i = 1; i <= n; i++) aa[i] = { i,rk[i],rk[i + L] };
			for(int i = 1; i <= n; i++) cnt[i] = 0;
			for(int i = 1; i <= n; i++) cnt[aa[i].y]++;
			for(int i = 1; i <= n; i++) cnt[i] += cnt[i - 1];
			for(int i = n; i >= 1; i--) bb[cnt[aa[i].y]--] = aa[i];
			for(int i = 1; i <= n; i++) cnt[i] = 0;
			for(int i = 1; i <= n; i++) cnt[aa[i].x]++;
			for(int i = 1; i <= n; i++) cnt[i] += cnt[i - 1];
			for(int i = n; i >= 1; i--) aa[cnt[bb[i].x]--] = bb[i];
			for(int i = 1; i <= n; i++)
				if((aa[i].x == aa[i - 1].x) && (aa[i].y == aa[i - 1].y))
					rk[aa[i].id] = rk[aa[i - 1].id];
				else rk[aa[i].id] = rk[aa[i - 1].id] + 1;
		} 
		for(int i = 1; i <= n; i++) sa[rk[i]] = i; int k = 0;
		for(int i = 1; i <= n; i++)
		{
			if(k) k--;
			int j = sa[rk[i] - 1];
			while((i + k <= n) && (j + k <= n) && (S[i + k] == S[j + k])) k++;
			height[rk[i]] = k;
		}
	}

	inline void buildst()
	{
		lg2[0] = -1; for(int i = 1; i < N; i++) lg2[i] = lg2[i / 2] + 1; lg2[0] = 0;
		for(int i = 1; i <= n; i++) st[i][0] = height[i];
		for(int j = 1; (1 << j) <= n; j++)
			for(int i = 1; i + (1 << j) - 1 <= n; i++)
				st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
	}

	inline int Lcp(int l, int r)
	{
		l = rk[l], r = rk[r];
		if(l > r) swap(l, r); l++;
		int k = lg2[r - l + 1];
		return min(st[l][k], st[r - (1 << k) + 1][k]);
	}
}SA[2];

int main()
{
	scanf("%d", &T);
	while(T--)
	{
		scanf("%s", SA[0].S + 1);
		int n = strlen(SA[0].S + 1);
		for(int i = 1; i <= n; i++) a[i] = b[i] = 0;
		for(int i = 1; i <= n; i++)
			SA[1].S[i] = SA[0].S[n - i + 1];
		SA[0].buildsa(), SA[1].buildsa();
		SA[0].buildst(), SA[1].buildst();

		for(int Len = 1; Len <= n / 2; Len++)
		{
			for(int i = Len; i <= n; i += Len)
			{
				int l = i, r = i + Len;
				int L = n - (r - 1) + 1, R = n - (l - 1) + 1;
				int lcp = SA[0].Lcp(l, r); lcp = min(lcp, Len);
				int lcs = SA[1].Lcp(L, R); lcs = min(lcs, Len - 1);
				if(lcp + lcs >= Len)
				{
					b[i - lcs]++, b[i - lcs + (lcp + lcs - Len + 1)]--;
					a[r + lcp - (lcp + lcs - Len + 1)]++, a[r + lcp]--;
				}
			}
		} 
		for(int i = 1; i <= n; i++) a[i] += a[i - 1], b[i] += b[i - 1];
		ll ans = 0;
		for(int i = 1; i < n; i++) ans += a[i] * b[i + 1];

		printf("%lld\n", ans);
	}
	return 0;
}