树状数组

树状数组

一种神奇的数据结构。

引子

当我们想要对一个数组进行单点加时，我们可以选择使用普通数组，时间复杂度是 \(O(1)\)；
当我们想要对一个数组进行区间求和时，我们可以选择使用前缀和数组，时间复杂度也是 \(O(1)\)；

但是，前缀和数组在进行单点加时，时间复杂度是 \(O(n)\) ；
而普通数组在进行区间求和时，时间复杂度也是 \(O(n)\) ；

我们能不能设计出一个数据结构，让我们在进行这两个操作时牺牲某一个操作的时间复杂度，而减少了另一个操作的时间复杂度呢？

于是，树状数组就应运而生。

简要介绍

树状数组的存储原理是这个样子的：

我们称原数组为 \(a[i]\) ，我们正常所输入的数据就存储在这里。

在原数组 \(a[i]\) 的基础上，我们创建一个新的数组 \(c[i]\) 。
数组 \(c[i]\) 是以这个规则存储信息的：

我们先列出所有的数组下标：

接下来我们开始考虑数字的 \(lowbit\) 。

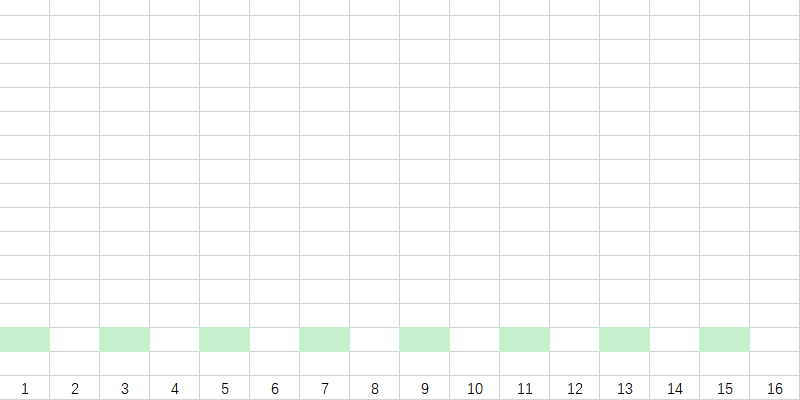
所有奇数的 \(lowbit\) 都是1。
我们在第一层标记上 \(lowbit\) 为1的所有数字：

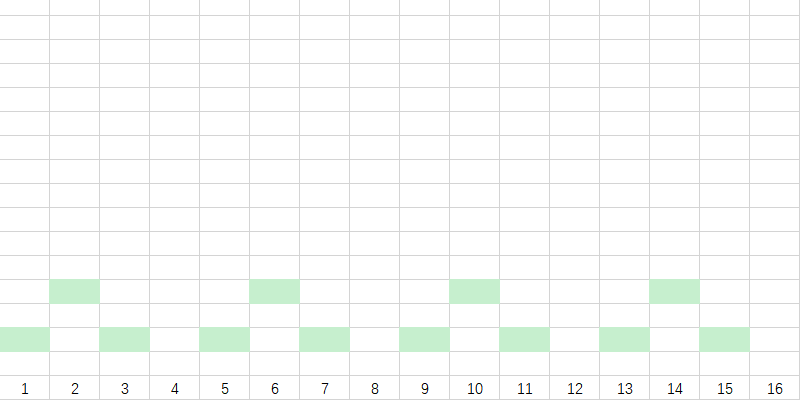
接下来，我们依次标上数字的 \(lowbit\) ：

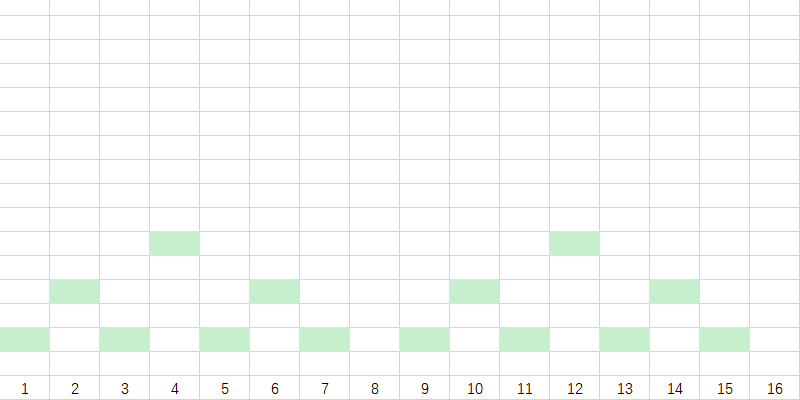
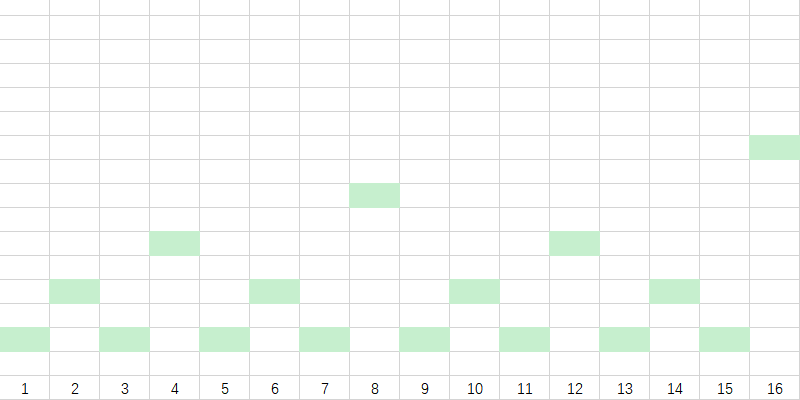
最后，我们再进行一下延长，每一个块向左延长至长度为 \(2^{lowbit(i)}\) 。

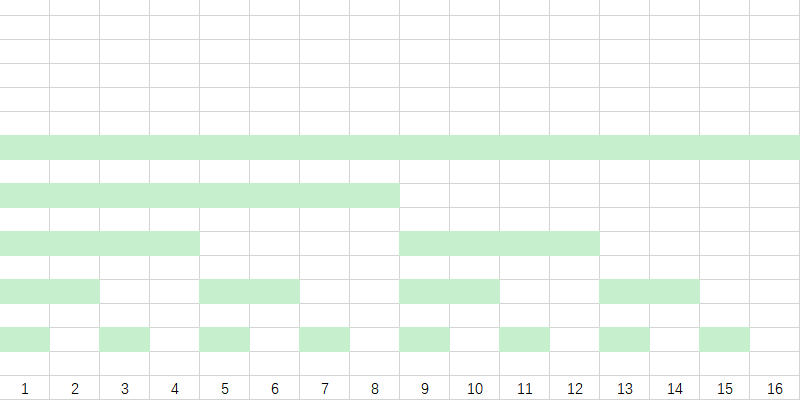
我们对块进行一下标号：

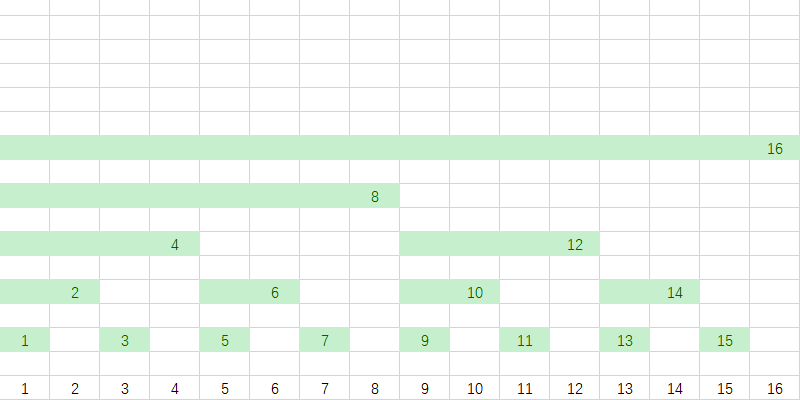
这些绿色的块里面存储的是其下方所有数字的和。

当然，我们进行值的更新的时候，不可能一个一个加起来再更新，这样复杂度又回到了原先的样子。

我们更新时遵循的是这样一个路线：

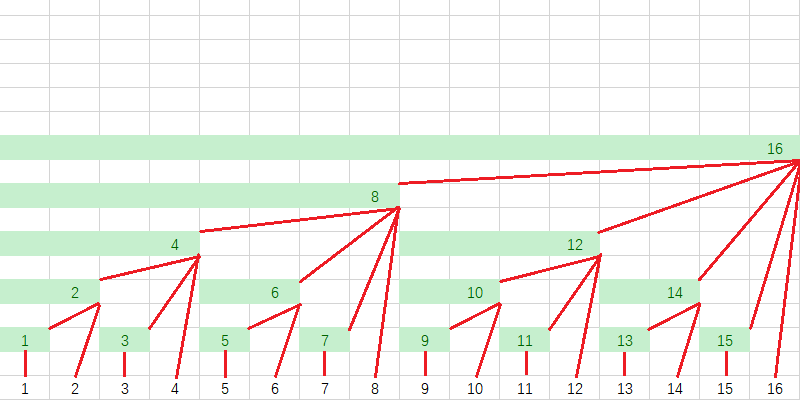
因为每一个数有 \(\log (n)\) 位，所以最终两个操作的时间复杂度都是 \(O(\log n)\) 。

板子

#include <bits/stdc++.h>
using namespace std;
const int N = 500010;
int a[N], tr[N];
int n, m;
int lowbit(int a)
{
	return a & -a;
}
void add(int x, int c)
{
	for(int i = x; i <= n; i += lowbit(i))
	{
		tr[i] += c;
	}
	return;
}
int sum(int x)
{
	int res = 0;
	for(int i = x; i; i -= lowbit(i))
	{
		res += tr[i];
	}
	return res;
}
int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i++)
	{
		cin >> a[i];
		add(i, a[i]);
	}
	for(int i = 1; i <= m; i++)
	{
		int op, x, y;
		cin >> op >> x >> y;
		if(op == 1)
		{
			a[x] += y;
			add(x, y);
		}
		else
		{
			int res = sum(y) - sum(x - 1);
			cout << res << endl;
		}
	}
	return 0;
}