排列相关
排列
排列指由 \([1,n]\) 范围内的所有整数组成的一个有序数列叫做 \(n\) 级排列。
逆序相关
逆序
逆序指大权排在小权后面。
逆序数
逆序数指逆序的总数,用 \(N(A_n)\) 来表示,其中括号里的是一个n级排列。
如果 \(N(A_n)=0\) ,那我们称这个排列为标准排列或者自然排列,其中所有元素都是按照顺序排列。
奇偶排列
对于一个n级排列 \(A_n\) ,如果 $N(A_n) \% 2 = 1 $ (即逆序数为奇数),那它是一个奇排列;反之( $N(A_n) \% 2 = 0 $ ,逆序数为偶数)则是一个偶排列。
这里有一个比较重要的定理:
\(n\) 级排列中,奇排列与偶排列各有 \(\dfrac{n!}{2}\) 个。
对换
对换即交换两个数的顺序,与我们常用的swap()函数类似。
对换一次之后会使排列的奇偶性翻转。
行列式
(本部分按照宋浩老师讲课顺序撰写,会出现部分引用)
今天AJ只给同学们留了一道题目作为作业:
解方程。
\[\begin{cases}
5x+6y=7 \\\\
9x+4y=3
\end{cases}
\tag {2.0.1}
\]
简单。
学过二元一次方程组的人都能做得出来。
我们首先消掉 \(x\) ,把方程组变成这个样子:
\[\begin{cases}
9 \times 5x + 9 \times 6y = 7 \times 9 \\\\
5 \times 9x + 5 \times 4y = 3 \times 5
\end{cases}
\tag{2.0.2}
\]
可得
\[\begin{align}
x & = \frac{7 \times 4 - 6 \times 3}{5 \times 4 - 6 \times 9} \tag{2.0.3} \\\\
y & = \frac{3 \times 5 - 7 \times 9}{5 \times 4 - 6 \times 9} \tag{2.0.4}
\end{align}
\]
然而班里唯一学过高等数学(现在不是了)的王哥用另一种方法做了出来。
二阶行列式
\[\begin{align}
x & = \frac{\begin{vmatrix} 7 & 6 \\\\ 3 & 4 \end{vmatrix}}{\begin{vmatrix} 5 & 6 \\\\ 9 & 4 \end{vmatrix}} \tag{2.1.1} \\\\
y & = \frac{\begin{vmatrix} 3 & 7 \\\\ 9 & 5 \end{vmatrix}}{\begin{vmatrix} 5 & 6 \\\\ 9 & 4 \end{vmatrix}} \tag{2.1.2}
\end{align}
\]
王哥后来解释道:“这玩意叫做二阶行列式。二阶行列式是这么用的:
\[\begin{vmatrix} a & b \\\\ c & d \end{vmatrix} = ad - bc
\tag{2.1.3}
\]
所以最终展开之后是大家得到的答案。”
于是,同学们开始广泛地瞎玩使用二阶行列式。
三阶行列式
但是tue不满足于二阶行列式。他追问:“有二阶的,是不是还会有三阶的?”
王哥:“是的。但是三阶行列式更加复杂。比如这个:
\[\begin{vmatrix}
a & b & c \\\\
d & e & f \\\\
g & h & i
\end{vmatrix}
= aei+bfg+cdh-afh-bdi-ceg
\tag{2.2.1}
\]
二阶行列式展开后的结果是主对角线上的数字相乘减去次对角线上的数字相乘,十分简单;但是三阶行列式就不一样了。它展开后的结果是这样的:
我们要把这个行列式在它的右边誊写一遍,像这样:
\[\begin{vmatrix}
a & b & c \\\\
d & e & f \\\\
g & h & i
\end{vmatrix}
\begin{vmatrix}
a & b & c \\\\
d & e & f \\\\
g & h & i
\end{vmatrix}
\tag{2.2.2}
\]
然后连线:
先连与主对角线平行的三条,不重复的连结所有数字

再连与次对角线平行的三条,不重复的连结所有数字
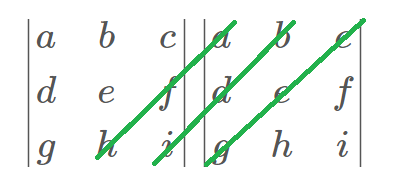
最后把三条蓝色线(与主对角线平行)上的数字分别相乘后求和减去三条绿色线(与次对角线平行)上的数字分别相乘之后的积之和。
就是这样:
\[\begin{vmatrix}
a & b & c \\\\
d & e & f \\\\
g & h & i
\end{vmatrix}
= \color{blue}{(aei+bfg+cdh)} - \color{green}{(afh+bdi+ceg)}
\tag{2.2.3}
\]
这样算起来十分麻烦,还容易算错,所以,现阶段我不建议使用三阶行列式。”
n阶行列式
\(n\) 阶行列式的展开遵循这样的规则:
- 首先列出所有列标的排列组合可能;
- 然后再分别算出每一个排列的奇偶性;
- 将每一个列标所对应的排列中的元素相乘,其中保证元素不重复(或者说行标取标准排列);
- 最后再将偶排列的和减去奇排列的和。
用式子表示大概就是这样:
\[\begin{vmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & \dots & a_{1,n} \\\\
a_{2,1} & a_{2,2} & a_{2,3} & \dots & a_{2,n} \\\\
a_{3,1} & a_{3,2} & a_{3,3} & \dots & a_{3,n} \\\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\\
a_{n,1} & a_{n,2} & a_{n,3} & \dots & a_{n,n}
\end{vmatrix}
=
\sum_{j1 , j2 , \dots , jn} (-1)^{N(j1 , j2 , \dots , jn)}
a_1 j_1 \ a_2 j_2 \ \dots a_n j_n
\tag{2.3.1}
\]
我们通常这样表示:$D (或 Det(a))= |a_{i,j}| $ 。
并且,显而易见的,特别地,\(|a_{1,1}| = a_{1,1}\) 。
然后我们会看见: \(\exists |a| \neq |a|\)
比如:\(|-1| \neq |-1|\) 。
因为左右两边一个是行列式,另一个是绝对值。
这个一定要分清。
特殊形态的行列式
有一些特殊的行列式,他们具有特殊的结构:
对角形行列式
形如
\[\begin{vmatrix}
a_{1,1} & & \\\\
& \ddots & \\\\
& & a_{n,n}
\end{vmatrix}
\tag{2.4.1}
\label{main}
\]
的行列式称为对角形行列式。
展开后的结果是: $D_{对角形} = \prod\limits_{i=1}^n a_{i,i} $ 。
上、下三角行列式
形如
\[\begin{vmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,n} \\\\
& a_{2,2} & a_{2,3} & \cdots & a_{2,n} \\\\
&& a_{3,3} & \cdots & a_{3,n} \\\\
&&& \ddots & \vdots \\\\
&&&& a_{n,n}
\end{vmatrix}
\tag{2.4.2}
\]
的行列式称作上三角行列式,而形如
\[\begin{vmatrix}
a_{1,1} &&&& \\\\
a_{2,1} & a_{2,2} &&& \\\\
a_{3,1} & a_{3,2} & a_{3,3} && \\\\
\vdots & \vdots & \vdots & \ddots & \\\\
a_{n,1} & a_{n,2} & a_{n,3} & \cdots & a_{n,n}
\end{vmatrix}
\tag{2.4.3}
\]
的称作下三角行列式。
展开后的结果是:\(D_{上三角}=(-1)^{\frac{n(n-1)}{2}}\prod\limits_{i-1}^n a_{i,i}\) ,\(D_{下三角}=(-1)^{\frac{n(n-1)}{2}}\prod\limits_{i-1}^n a_{i,i}\)
记住:不论是对角形还是上下三角,用的都是主对角线。
范德蒙德行列式
跳转:范德蒙德行列式
对称行列式
跳转:对称行列式
反对称行列式
跳转:反对称行列式
行列式的性质
转置
与矩阵一样,行列式也可以进行转置。
行列式 \(D\) 转置之后的行列式,我们称其为 行列式 \(D\) 的转置行列式,记作 \(D^T\) 或者 \(D'\) (少用)。
性质
\((D^T)^T \equiv D\) .
性质
性质1
\(D^T=D\) .
这里我们要注意:在行列式中,对行成立的性质,对列也成立。
性质2
两行(列)互换,行列式的值要变号。
推论:两行(列)相等,\(D = 0\) .
性质3
某一行(列)都乘k,相当于k乘以D。
\[\begin{vmatrix}a&b&c\\\\kd&ke&kf\\\\g&h&i\end{vmatrix}
=k
\begin{vmatrix}a&b&c\\\\d&e&f\\\\g&h&i\end{vmatrix}
\tag{2.5.1}
\]
推论:某一行(列)有公因子k,k可以提到外面去。
性质4
两行(列)对应成比例,行列式的值等于0。
推论:如果行列式某一行(列)等于0,行列式等于0。
性质5
\[\begin{vmatrix}
a&b&c\\\\d+d'&e+e'&f+f'\\\\g&h&i
\end{vmatrix}
=
\begin{vmatrix}
a&b&c\\\\d&e&f\\\\g&h&i
\end{vmatrix}
+
\begin{vmatrix}
a&b&c\\\\d'&e'&f'\\\\g&h&i
\end{vmatrix}
\tag{2.5.2}
\]
注意:这个只针对于某一行(列),其余的行(列)不变!
性质6
某一行(列)乘以一个数,加到另一行(列)上去,行列式的值不变。
好了,现在让我们利用这些性质,将这个行列式变为上三角行列式吧!
\[\begin{align}
D={} &
\begin{vmatrix}
1&2&0&1\\\\2&3&10&0\\\\0&3&5&18\\\\5&10&15&4
\end{vmatrix}\\\\
={} &
\begin{vmatrix}
1&2&0&1\\\\2+1\times(-2)&3+2\times(-2)&10+0\times(-2)&0+1\times(-2)\\\\0&3&5&18\\\\5&10&15&4
\end{vmatrix}\\\\
={} &
\begin{vmatrix}
1&2&0&1\\\\\color{red}{0}&-1&10&-2\\\\0&3&5&18\\\\5+1\times(-5)&10+2\times(-5)&15+0\times(-5)&4+1\times(-5)
\end{vmatrix}\\\\
={} &
\begin{vmatrix}
1&2&0&1\\\\\color{red}{0}&-1&10&-2\\\\0+0\times 3&3+(-1)\times 3&5+10\times 3&18+(-2)\times 3\\\\0&0&15&-1
\end{vmatrix}\\\\
={} &
\begin{vmatrix}
1&2&0&1\\\\\color{red}{0}&-1&10&-2\\\\\color{red}{0}&\color{red}{0}&35&12\\\\0+0\times(-\frac{3}{7})&0+0\times(-\frac{3}{7})&15+35\times(-\frac{3}{7})&-1+12\times(-\frac{3}{7})
\end{vmatrix}\\\\
={} &
\begin{vmatrix}
1&2&0&1\\\\\color{red}{0}&-1&10&-2\\\\\color{red}{0}&\color{red}{0}&35&12\\\\\color{red}{0}&\color{red}{0}&\color{red}{0}&-\frac{43}{7}
\end{vmatrix}\\\\
={} & 215
\end{align}
\tag{2.5.3}
\]
在解这一些行列式的时候,我们通常用这个顺序来解:
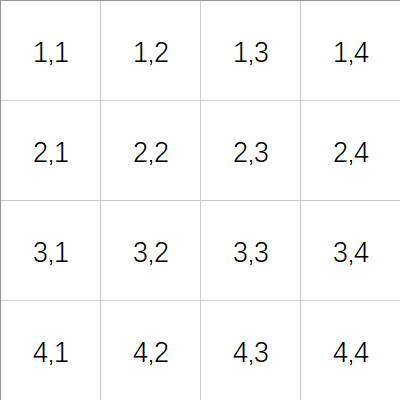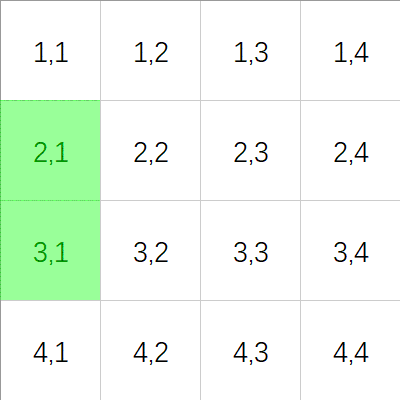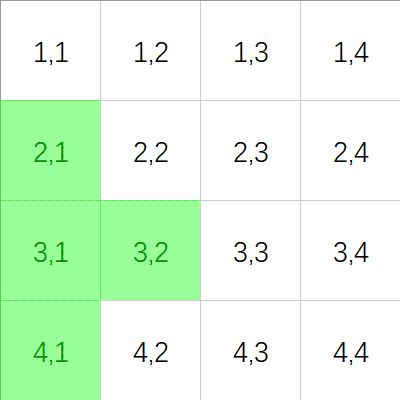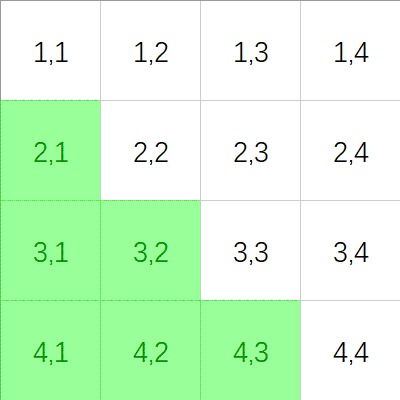
子式与余子式
我们去掉一个\(n\)阶行列式\(D_{n \times n}\)的 \(k\) 行与 \(k\) 列之后,我们就得到了它的一个 \(k\) 阶余子式。
例如这个行列式:
\[\begin{vmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4} \\\\
a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} \\\\
a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} \\\\
a_{4,1} & a_{4,2} & a_{4,3} & a_{4,4}
\end{vmatrix}
\tag{2.6.1}
\]
我们取走 \(a_{3,2}\) 所在的行与列之后,得到的行列式是这样的:
\[\begin{vmatrix}
a_{1,1} & a_{1,3} & a_{1,4} \\\\
a_{2,1} & a_{2,3} & a_{2,4} \\\\
a_{4,1} & a_{4,3} & a_{4,4}
\end{vmatrix}
\tag{2.6.2}
\]
我们称这样得到的余子式为 \(M_{3,2}\) 。
如果我们将 \(M_{3,2}*(-1)^{3+2}\) 的话,我们就得到了原行列式的代数余子式,记作\(A_{3,2}\) 。
定理1
\(D = \sum\limits_{j=1}^{n} a_{i,j}A_{i,j}\), 或 \(D = \sum\limits_{i=1}^{n} a_{i,j}A_{i,j}\)
定理2
某一行元素与另一行元素的代数余子式乘积之和为0。
子式
对于一个\(n\)阶行列式\(D_{n \times n}\),我们取其中的\(k\)行\(k\)列的交点,可以得到一个\(k\)阶的行列式。
如:
\[\begin{vmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & \dots & a_{1,n} \\\\
a_{2,1} & a_{2,2} & a_{2,3} & \dots & a_{2,n} \\\\
a_{3,1} & a_{3,2} & a_{3,3} & \dots & a_{3,n} \\\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\\
a_{n,1} & a_{n,2} & a_{n,3} & \dots & a_{n,n}
\end{vmatrix}
\tag{2.6.3}
\]
这个行列式的一个\(k\)阶子式可以是
\[\begin{vmatrix}
a_{i,j} & \cdots & a_{i,j+k} \\\\
\vdots & \ddots & \vdots \\\\
a_{i+k,j} & \cdots & a_{i+k,j+k}
\end{vmatrix}
\tag{2.6.4}
\]
拉普拉斯(Laplace)定理
取定\(k\)行,由\(k\)行元素组成的所有\(k\)阶子式与代数余子式乘积之和\(=D\) 。
例:
行列式
\[\begin{vmatrix}
1&2&0&0&0\\\\3&4&0&0&0\\\\1&2&3&4&5\\\\1&1&1&1&1\\\\6&6&8&3&1
\end{vmatrix}
\tag{2.7.1}
\]
可以被分解为
\[\begin{vmatrix}
1&2\\\\3&4
\end{vmatrix}
+(-1)^{1+2+1+2}\
\begin{vmatrix}
3&4&5\\\\1&1&1\\\\8&3&1
\end{vmatrix}
\tag{2.7.2}
\]
,即
\[\begin{vmatrix}
1&2&0&0&0\\\\3&4&0&0&0\\\\1&2&3&4&5\\\\1&1&1&1&1\\\\6&6&8&3&1
\end{vmatrix}
=\begin{vmatrix}
1&2\\\\3&4
\end{vmatrix}
+(-1)^{1+2+1+2}\
\begin{vmatrix}
3&4&5\\\\1&1&1\\\\8&3&1
\end{vmatrix}
\tag{2.7.3}
\]
行列式的运算
行列式相乘
同阶行列式相乘类似矩阵的点乘。
例:
\[\begin{gather}
\begin{vmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\\\ a_{2,1} & a_{2,2} & a_{2,3} \\\\ a_{3,1} & a_{3,2} & a_{3,3}
\end{vmatrix}
\times
\begin{vmatrix}
b_{1,1} & b_{1,2} & b_{1,3} \\\\ b_{2,1} & b_{2,2} & b_{2,3} \\\\ b_{3,1} & b_{3,2} & b_{3,3}
\end{vmatrix}
= \\\\ \notag
\begin{vmatrix}
a_{1,1}b_{1,1}+a_{1,2}b_{2,1}+a_{1,3}b_{3,1} & a_{1,1}b_{1,2}+a_{1,2}b_{2,2}+a_{1,3}b_{3,2} &
a_{1,1}b_{1,3}+a_{1,2}b_{2,3}+a_{1,3}b_{3,3} \\\\
a_{2,1}b_{1,1}+a_{2,2}b_{2,1}+a_{2,3}b_{3,1} & a_{2,1}b_{1,2}+a_{2,2}b_{2,2}+a_{2,3}b_{3,2} &
a_{2,1}b_{1,3}+a_{2,2}b_{2,3}+a_{2,3}b_{3,3} \\\\
a_{3,1}b_{1,1}+a_{3,2}b_{2,1}+a_{3,3}b_{3,1} & a_{3,1}b_{1,2}+a_{3,2}b_{2,2}+a_{3,3}b_{3,2} &
a_{3,1}b_{1,3}+a_{3,2}b_{2,3}+a_{3,3}b_{3,3}
\end{vmatrix} \notag
\end{gather}
\tag{2.8.1}
\]
如果行列式不同阶,那么就把高阶的降阶。
加边法
假如有一个行列式如下:
\[\begin{vmatrix}
1+a_1 & 1 & 1 & \cdots & 1 \\\\
1 & 1+a_2 & 1 & \cdots & 1 \\\\
1 & 1 & 1+a_3 & \cdots & 1 \\\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\\
1 & 1 & 1 & \cdots & 1+a_n
\end{vmatrix}
\tag{2.8.2}
\]
我们在解这个行列式的时候,可以给这个行列式在最左面加一列0,再在最上面加一行1,如下:
\[\begin{vmatrix}
1 & 1 & 1 & 1 & \cdots & 1\\\\
0 & 1+a_1 & 1 & 1 & \cdots & 1 \\\\
0 & 1 & 1+a_2 & 1 & \cdots & 1 \\\\
0 & 1 & 1 & 1+a_3 & \cdots & 1 \\\\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\\\
0 & 1 & 1 & 1 & \cdots & 1+a_n
\end{vmatrix}
\tag{2.8.3}
\]
此时,我们再对这个行列式做出进一步的计算:
\[= \begin{vmatrix}1&1&1&\cdots&1\\\\-1&a_1&&&\\\\-1&&a_2&&\\\\\vdots&&&\ddots&\\\\-1&&&&a_n\end{vmatrix}
\tag{2.8.4}
\label{tri}
\]
\[= \begin{vmatrix}x&1&1&\cdots&1\\\\&a_1&&&\\\\&&a_2&&\\\\&&&\ddots&\\\\&&&&a_n\end{vmatrix}
\tag{2.8.5}
\]
其中,\(x=1+ \sum\limits_{i=1}^{n} \dfrac{1}{a_i}\) 。
注意:加边的时候不能改变行列式的值!
其中的\(\ref{tri}\) 叫做“三叉形行列式”。
特殊行列式(2)
范德蒙德(Vandermonde)行列式
形如
\[\begin{vmatrix}
1 & 1 & 1 & \cdots & 1 \\\\
x_1 & x_2 & x_3 & \cdots & x_n \\\\
x^2_1 & x^2_2 & x^2_3 & \cdots &x^2_n\\\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\\
x^{n-1}_1 & x^{n-1}_2 & x^{n-1}_3 & \cdots & x^{n-1}_n
\end{vmatrix}
\tag{2.9.1}
\]
的行列式叫做范德蒙德行列式。
其结果是这样的:
\[\begin{vmatrix} x_1^0 & \cdots & x_n^0 \\\\ \vdots & \ddots & \vdots \\\\ x_1^{n-1} & \cdots & x_n^{n-1} \end{vmatrix} = \prod_{i=j=1}^n (x_i-x_j) \tag{2.9.2}
\]
对称行列式
形如
\[\begin{vmatrix}
x & a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\\\
a_{1,1} & x & a_{2,2} & \cdots & a_{2,n} \\\\
a_{1,2} & a_{2,2} & x & \cdots & a_{3,n} \\\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\\
a_{1,n} & a_{2,n} & a_{3,n} & \cdots & x
\end{vmatrix}
\tag{2.9.3}
\]
的行列式叫做对称行列式,即\(a_{i,j}=a_{j,i}\)。
对称行列式中:
反对称行列式
形如
\[\begin{vmatrix}
0 & a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\\\
-a_{1,1} & 0 & a_{2,2} & \cdots & a_{2,n} \\\\
-a_{1,2} & -a_{2,2} & 0 & \cdots & a_{3,n} \\\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\\
-a_{1,n} & -a_{2,n} & -a_{3,n} & \cdots & 0
\end{vmatrix}
\tag{2.9.4}
\]
的行列式叫做反对称行列式,即\(a_{i,j}=-a_{j,i}\)。
反对称行列式中:
在奇数阶反对称行列式中,\(D=0\) ;
证明:
\[\begin{gathered}
\because
\begin{cases}
D=D^T \\\\
D=-D^T
\end{cases}
\\\\
\therefore D=-D \\\\
\therefore 2D=0 \\\\
\therefore D=0
\end{gathered}
\tag{2.9.5}
\]
克拉默(Cramer)法则
就像这里所说的那样,行列式可以用来解多元一次方程组。
比如下面这个:
\[\begin{cases}
x_1+x_2+x_3=1\\\\
x_1-x_2+5x_3=6\\\\
-x_1+x_2+6x_3=9
\end{cases}
\]
其中,
\[\begin{cases}
x_1=\frac{D_1}{D}\\\\
x_2=\frac{D_2}{D}\\\\
x_3=\frac{D_3}{D}
\end{cases}
\tag{2.10.1}
\]
其中,
\[\begin{cases}
D=\begin{vmatrix}1&1&1\\\\1&-1&5\\\\-1&1&6\end{vmatrix}\\\\
D_1=\begin{vmatrix}1&1&1\\\\6&-1&5\\\\9&1&6\end{vmatrix}\\\\
D_2=\begin{vmatrix}1&1&1\\\\1&6&5\\\\-1&9&6\end{vmatrix}\\\\
D_3=\begin{vmatrix}1&1&1\\\\1&-1&6\\\\-1&1&9\end{vmatrix}
\end{cases}
\tag{2.10.2}
\]
简化一点,就是这样:
\[\begin{gather}
\begin{cases}
a_1x_1+b_1x_2+c_1x_3=d_1\\\\
a_2x_1+b_2x_2+c_2x_3=d_2\\\\
a_3x_1+b_3x_2+c_3x_3=d_3
\end{cases}\\\\
\tag{2.10.3}
\text{其中,}\\\\
\begin{cases}
x_1=\frac{D_1}{D}\\\\
x_2=\frac{D_2}{D}\\\\
x_3=\frac{D_3}{D}
\end{cases}\\\\
\tag{2.10.4}
\text{其中,}\\\\
\begin{cases}
D=\begin{vmatrix}a_1&b_1&c_1\\\\a_2&b_2&c_2\\\\a_3&b_3&c_3\end{vmatrix}\\\\
D_1=\begin{vmatrix}d_1&b_1&c_1\\\\d_2&b_2&c_2\\\\d_3&b_3&c_3\end{vmatrix}\\\\
D_2=\begin{vmatrix}a_1&d_1&c_1\\\\a_2&d_2&c_2\\\\a_3&d_3&c_3\end{vmatrix}\\\\
D_3=\begin{vmatrix}a_1&b_1&d_1\\\\a_2&b_2&d_2\\\\a_3&b_3&d_3\end{vmatrix}
\end{cases}
\tag{2.10.5}
\end{gather}
\]
矩阵
形如
\[A =
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & \dots & a_{1,n} \\\\
a_{2,1} & a_{2,2} & a_{2,3} & \dots & a_{2,n} \\\\
a_{3,1} & a_{3,2} & a_{3,3} & \dots & a_{3,n} \\\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\\
a_{m,1} & a_{m,2} & a_{m,3} & \dots & a_{m,n}
\end{bmatrix}
\tag{3.0.1}
\]
的数据结构,我们称之为大小为 \(m*m\) 的矩阵,可以简记为 \(A_{m \times n}\) 。
显而易见,\(\begin{bmatrix}n\end{bmatrix}=n\)。
特殊形态的矩阵
行矩阵
只有一行的矩阵。
例:\(A_{1 \times 3}=\begin{bmatrix}1&1&1\end{bmatrix}\)
列矩阵
只有一列的矩阵。
例:\(A_{3 \times 1}=\begin{bmatrix}1\\\\1\\\\1\end{bmatrix}\)
零矩阵
只有零的矩阵。
例:\(A_{2 \times 2}=\begin{bmatrix}0&0\\\\0&0\end{bmatrix}\)
零矩阵可以记作\(0\)。
负矩阵
假设有一个矩阵\(A\),其负矩阵为\(-A\) 。
某一个矩阵的负矩阵中的每一个元素都与原矩阵的对应元素互为相反数。
方阵
行数等于列数的矩阵。
例:\(A_{2 \times 2}=\begin{bmatrix}1&1\\\\1&1\end{bmatrix}\)
\(n\)阶矩阵\(A_{n \times n}\)简便记作\(A_n\)。
单位矩阵
与单位行列式类似,即主对角线上均为1,其余均为0的矩阵。
例:\(A_{n \times n}=\begin{bmatrix}1&&\\\\&\ddots&\\\\&&1\end{bmatrix}\)
单位矩阵可以记作\(E\)或\(I\)。
矩阵的运算
矩阵有这样几种运算:
矩阵的相等
没想到吧矩阵的相等在我这里也算作一种运算
两个矩阵相等的前提是他们是同型矩阵。如:
如果\(A_{m,n}=B_{p,q}\),
那么\(m=p,n=q\),且\(\forall a_{i,j}=b_{i,j}\)
加法、减法
\[\begin{bmatrix}
a & b & c \\\\
d & e & f
\end{bmatrix}
\pm
\begin{bmatrix}
g & h & i \\\\
j & k & l
\end{bmatrix}
=
\begin{bmatrix}
a \pm g & b \pm h & c \pm i \\\\
d \pm j & e \pm k & f \pm l
\end{bmatrix}
\tag{3.1.1}
\]
矩阵的加法满足交换律和结合律。
注意:只有同型矩阵之间才能加减。
数乘
\[k \times
\begin{bmatrix}
a & b & c \\\\
d & e & f
\end{bmatrix}
=
\begin{bmatrix}
ka & kb & kc \\\\
kd & ke & kf
\end{bmatrix}
\tag{3.2.1}
\]
矩阵的数乘满足交换律、结合律和分配律。
矩阵提公因子
与行列式不同(这一点可以在上面的数乘部分看到),矩阵提公因子的话是整体提取的。如:
\[\begin{bmatrix}
ka & kb & kc \\\\
kd & ke & kf
\end{bmatrix}
=k\times
\begin{bmatrix}
a & b & c \\\\
d & e & f
\end{bmatrix}
\tag{3.2.2}
\]
点乘
如果
\[A_{i,k} \times B_{k,j} = C_{i,j}
\tag{3.3.1}
\]
的话,那么
\[c_{i,j}=\sum_{k}^{\infty} \ a_{i,k} \times b_{k,j}
\tag{3.3.2}
\]
,其中 $ a_{i,k} \in A , b_{k,j} \in B , c_{i,j} \in C $ 。
矩阵的点乘要求A矩阵的长与B矩阵的宽相等。
例:
\[\begin{gather}
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\\\ a_{2,1} & a_{2,2} & a_{2,3} \\\\ a_{3,1} & a_{3,2} & a_{3,3} \\\\ a_{4,1} & a_{4,2} & a_{4,3}
\end{bmatrix}
\times
\begin{bmatrix}
b_{1,1} & b_{1,2} \\\\ b_{2,1} & b_{2,2} \\\\ b_{3,1} & b_{3,2}
\end{bmatrix}\\\\ \notag
=\\\\ \notag
\begin{bmatrix}
a_{1,1}b_{1,1}+a_{1,2}b_{2,1}+a_{1,3}b_{3,1} & a_{1,1}b_{1,2}+a_{1,2}b_{2,2}+a_{1,3}b_{3,2} \\\\
a_{2,1}b_{1,1}+a_{2,2}b_{2,1}+a_{2,3}b_{3,1} & a_{2,1}b_{1,2}+a_{2,2}b_{2,2}+a_{2,3}b_{3,2} \\\\
a_{3,1}b_{1,1}+a_{3,2}b_{2,1}+a_{3,3}b_{3,1} & a_{3,1}b_{1,2}+a_{3,2}b_{2,2}+a_{3,3}b_{3,2} \\\\
a_{4,1}b_{1,1}+a_{4,2}b_{2,1}+a_{4,3}b_{3,1} & a_{4,1}b_{1,2}+a_{4,2}b_{2,2}+a_{4,3}b_{3,2}
\end{bmatrix} \notag
\end{gather}
\tag{3.3.3}
\label{dt}
\]
在点乘中,有许多需要注意的点:
注意
1.矩阵的点乘不满足交换律。
即,\(A \times B\)不一定\(=B \times A\)。
所以,特别的,在算式\(A \times B\)中,我们称\(A\)左乘\(B\),同时\(B\)右乘\(A\)。
如果正好\(A \times B=B \times A\),那么我们称\(A,B\)是可交换的。
但是,矩阵的点乘满足结合律和分配律,即:
\((A \times B) \times C=A \times (B \times C)\)
运用分配率的时候需要注意,矩阵的位置要对应。
$(A+B) \times C = A \times C + B \times C $
\(C \times (A \times B) = C \times A + C \times B\)
2.\(A \times B=0 \ \nRightarrow A=0 \ or \ B=0\).
3.\(if \ A \times B=A \times C , A \neq 0 \nRightarrow B=C\)
性质
- \(A \times 0 = 0\).
- \(A \times E=E \times A=A\).
- \(k(A \times B) = (kA) \times B = A \times (kB)\)
转置
将矩阵的行和列互相交换之后,就完成了矩阵的转置。
如:
\[\begin{bmatrix}
a & b & c \\\\
d & e & f
\end{bmatrix}^T=
\begin{bmatrix}
a & d\\\\
b & e\\\\
c & f
\end{bmatrix}
\tag{3.4.1}
\]
矩阵 \(A\) 的转置用符号 \(A^T\) 表示。
性质
- \((A^T)^T=A\).
- \((A+B)^T=A^T+B^T\).
- \((kA)^T=kA^T\).
- \((AB)^T=B^T \times A^T\).
幂运算
与常数类似,矩阵也有幂运算。
我们定义矩阵\(A\)的\(k\)次幂为\(A\) \(k\)次自乘后所得的结果,即
\[A^k=\underbrace{A \times A \times A \times \cdots \times A}_{k\text{个}}
\tag{3.5.1}
\]
特别的,我们定义\(A^0=E\)。
矩阵的幂运算与常数的幂运算不是很类似。
矩阵的幂运算不满足这些定律:
\((A \times B)^k \neq A^k \times B^k\)
\((A \pm B)^2 \neq A^2 \pm 2A \times B +B^2\)
但是,矩阵满足这样一个奇怪的东西:
\((A+E)^2 = A^2 + 2A \times E + E^2\)
我们推导一下,可以得到这样一个结果:
\[\begin{align}
(A+E)^2 ={} & (A+E) \times (A+E) \\\\
={} & (A^2 + E \times A) + (A \times E + E^2) \\\\
\end{align}
\]
\[\because A \times E = E \times A = A \\\\
\therefore
\begin{align}
(A+E)^2 ={} & (A^2 + A \times E) + (A \times E + E^2) \\\\
={} & A^2 + 2A \times E + E^2
\end{align}
\]

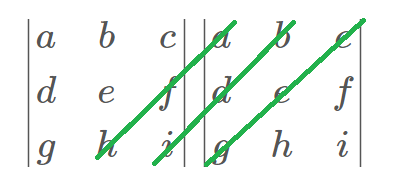



 浙公网安备 33010602011771号
浙公网安备 33010602011771号