OO第一单元作业总结

第一次作业

类的设计

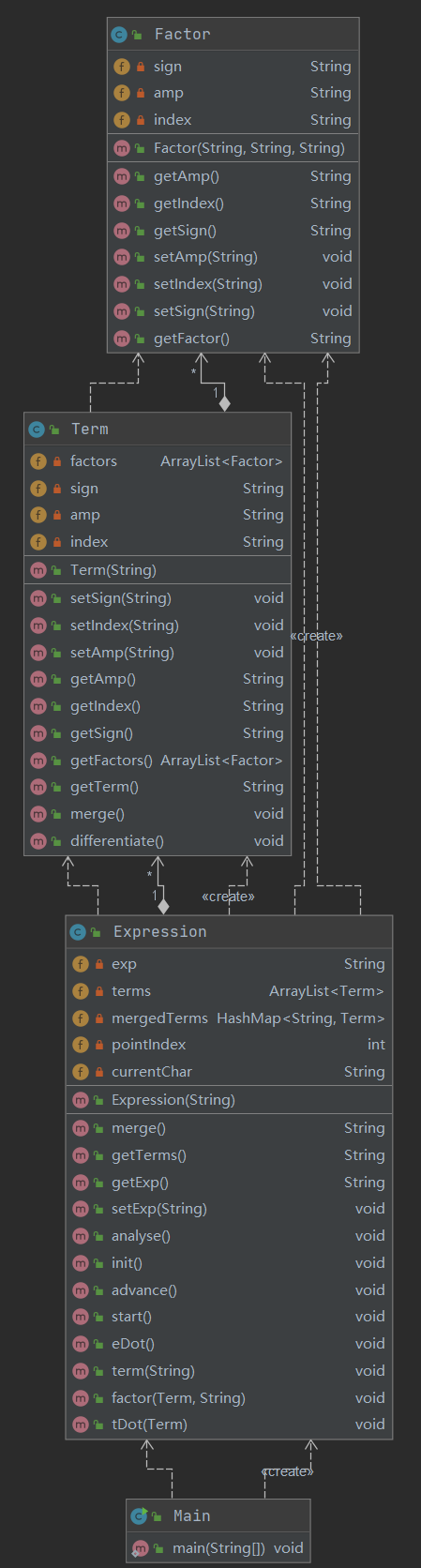
方法度量:

Method	CogC	ev(G)	iv(G)	v(G)
Expression.analyse()	0.0	1.0	1.0	1.0
Expression.eDot()	5.0	2.0	3.0	4.0
Expression.Expression(String)	0.0	1.0	1.0	1.0
Expression.factor(Term,String)	10.0	2.0	5.0	5.0
Expression.getExp()	0.0	1.0	1.0	1.0
Expression.getTerms()	1.0	1.0	2.0	2.0
Expression.init()	0.0	1.0	1.0	1.0
Expression.merge()	24.0	2.0	10.0	11.0
Expression.setExp(String)	0.0	1.0	1.0	1.0
Expression.start()	3.0	1.0	3.0	3.0
Expression.tDot(Term)	6.0	3.0	3.0	5.0
Expression.term(String)	3.0	1.0	3.0	3.0
Factor.Factor(String,String,String)	14.0	1.0	8.0	11.0
Factor.getAmp()	0.0	1.0	1.0	1.0
Factor.getFactor()	5.0	4.0	2.0	5.0
Factor.getIndex()	0.0	1.0	1.0	1.0
Factor.getSign()	0.0	1.0	1.0	1.0
Factor.setAmp(String)	0.0	1.0	1.0	1.0
Factor.setIndex(String)	0.0	1.0	1.0	1.0
Factor.setSign(String)	0.0	1.0	1.0	1.0
Main.main(String[])	1.0	1.0	2.0	2.0
null.compare(Entry,Entry)	2.0
Term.differentiate()	6.0	1.0	2.0	5.0
Term.getAmp()	0.0	1.0	1.0	1.0
Term.getFactors()	0.0	1.0	1.0	1.0
Term.getIndex()	0.0	1.0	1.0	1.0
Term.getSign()	0.0	1.0	1.0	1.0
Term.getTerm()	6.0	6.0	4.0	6.0
Term.merge()	6.0	1.0	3.0	5.0
Term.setAmp(String)	0.0	1.0	1.0	1.0
Term.setIndex(String)	0.0	1.0	1.0	1.0
Term.setSign(String)	0.0	1.0	1.0	1.0
Term.Term(String)	0.0	1.0	1.0	1.0
Total	94.0	46.0	71.0	88.0
Average	2.764705882352941	1.393939393939394	2.1515151515151514	2.6666666666666665

第一次完全没有任何继承和接口的使用，但仔细看其实只是把方法和数据段做了分类，配合递归下降算法，彼此之间来回调用。

面向对象的设计思路还局限在抽象出不同对象，存储不同字段和方法的层面上。

算法

写第一次作业的时候就直接用了递归下降的方法：

当时根据课程提供的表达式形式化表述，大致做了消除左递归，得到自己的表达式如下：

e -> [op]term e'
e' -> (op) term | ""
term -> [op] factor t'
t' -> * factor t' | ""
factor -> poly | const

递归下降的逻辑全部封装在Expression类内，按表达式调用

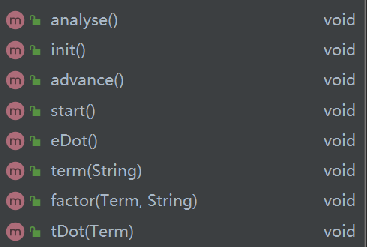
除了递归下降的方法，我个人还倾向利用正则来辅助递归下降。

比如在第一次作业保证格式合法的情况下，其实可以把符号压缩，诸如：

 exp.replace("++","+");

（但是本人考虑既然已经实现了递归下降，其实这种做法可有可无）

比如在进入factor函数匹配factor内容的时候，我直接改用正则匹配：

String polyRegex = "(?<poly>x(\\*\\*(?<index>[+-]?[0-9]*))*)";
String constRegex = "(?<const>(?<amp>[+-]?[0-9]*))";

就避免了继续递归下降读取各个部分，直接按factor的两种形式匹配到位，把参数分离传入对应类的构造器即可。

优化

• 在求导后的合并中可以看到多处定义了merge()方法

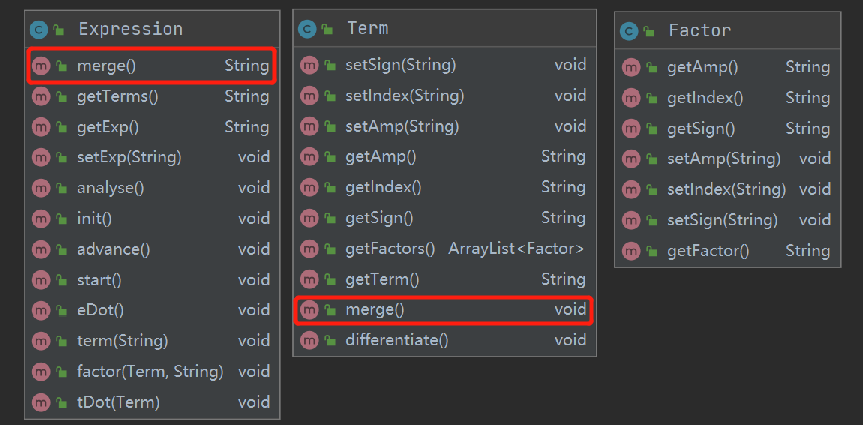
其实这里完全可以定义一个merge（）的接口，由两个类实现。

• 在第一次研讨课上受到同学启发，其实e‘ 和 t’ 的部分可以直接写一个while循环就可以，还能减少递归的栈数增长。这部分在第二次作业重构的时候已经实现。

• 可以看到为了处理多符号问题，在两个类中都加入了对符号的存储。

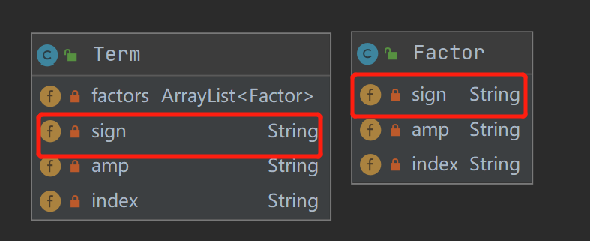
首先，其实对于符号最好的处理办法是用之前提到的把连续符号都吃掉（表达式绝对合法）

就算不吃掉符号，在factor把系数里的符号特意分出来存到sign里，然后在输出的时候再拼回去也是不必要的。然而我在折磨完后才发现自己设计上的谬误。这部分在第二次重构的时候也完全修正了。

测评

• 强测和互测都通过了，但是发现自己忘记判系数为0，导致一个性能分炸了。（这个还是上面我在factor里设计sign的问题，代码过于臃肿导致没能发现）
• 在阅读其他同学代码的时候学习到了正则预查的知识。发现用正则预查的方式split可以做到既不占用符号位，又能完美分割各个项的神奇方法。

第二次作业

类的设计

第二次作业由于引入了递归嵌套，难度陡增，不说正则几乎站不住脚，就是第一次用了递归下降的写法，我也直接选择了重构。

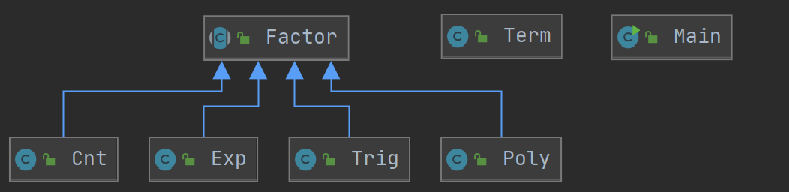
总体视图

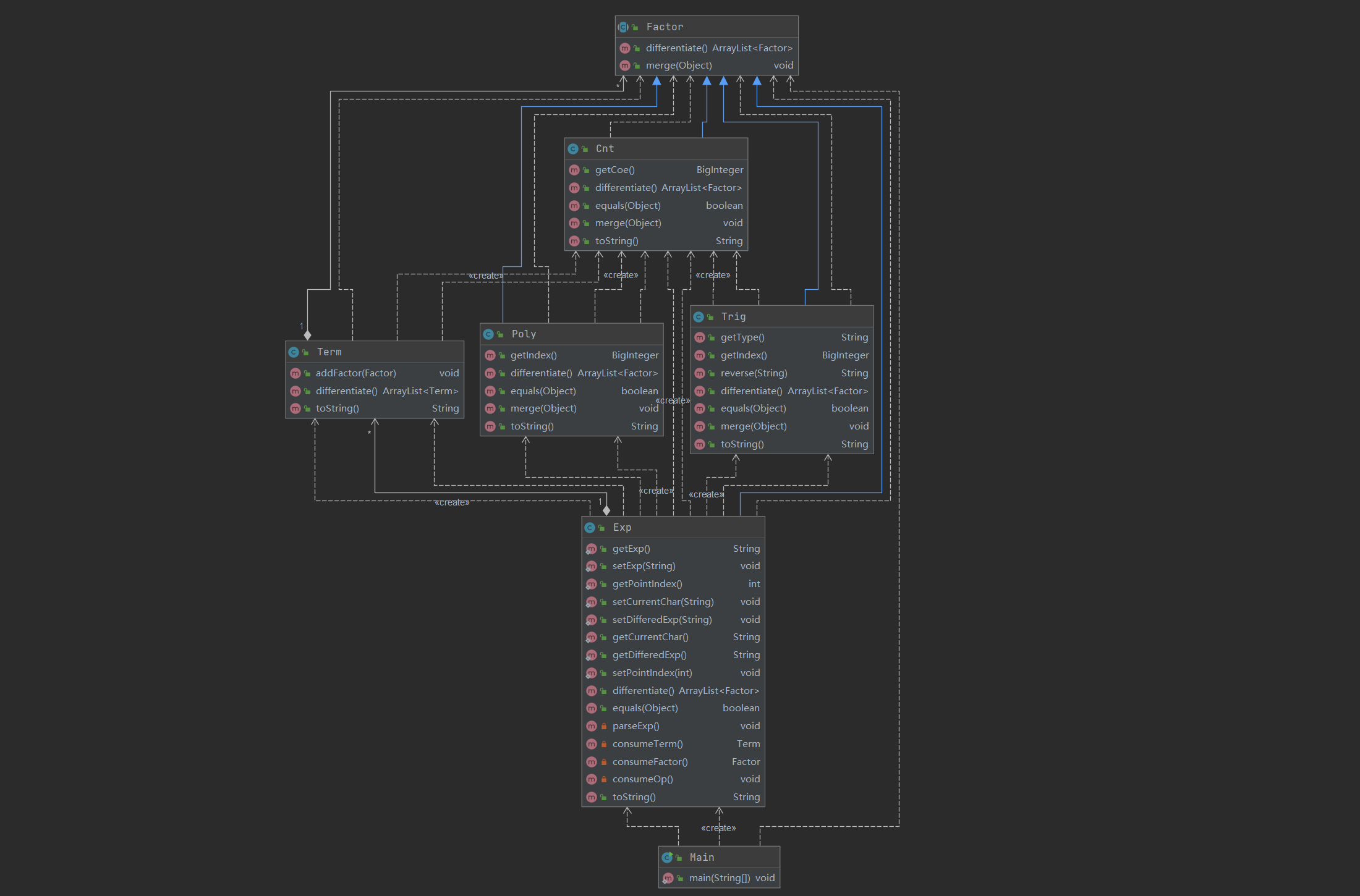
方法度量：

Method	CogC	ev(G)	iv(G)	v(G)
Cnt.Cnt(String)	0.0	1.0	1.0	1.0
Cnt.differentiate()	0.0	1.0	1.0	1.0
Cnt.equals(Object)	5.0	3.0	1.0	3.0
Cnt.getCoe()	0.0	1.0	1.0	1.0
Cnt.merge(Object)	0.0	1.0	1.0	1.0
Cnt.toString()	0.0	1.0	1.0	1.0
Exp.consumeFactor()	19.0	7.0	9.0	10.0
Exp.consumeOp()	2.0	1.0	2.0	2.0
Exp.consumeTerm()	9.0	3.0	6.0	6.0
Exp.differentiate()	1.0	1.0	2.0	2.0
Exp.equals(Object)	0.0	1.0	1.0	1.0
Exp.Exp()	0.0	1.0	1.0	1.0
Exp.Exp(ArrayList)	0.0	1.0	1.0	1.0
Exp.Exp(String)	0.0	1.0	1.0	1.0
Exp.getCurrentChar()	0.0	1.0	1.0	1.0
Exp.getDifferedExp()	0.0	1.0	1.0	1.0
Exp.getExp()	0.0	1.0	1.0	1.0
Exp.getPointIndex()	0.0	1.0	1.0	1.0
Exp.parseExp()	2.0	1.0	3.0	3.0
Exp.setCurrentChar(String)	0.0	1.0	1.0	1.0
Exp.setDifferedExp(String)	0.0	1.0	1.0	1.0
Exp.setExp(String)	0.0	1.0	1.0	1.0
Exp.setPointIndex(int)	0.0	1.0	1.0	1.0
Exp.toString()	6.0	3.0	3.0	6.0
Factor.differentiate()	0.0	1.0	1.0	1.0
Factor.merge(Object)	0.0	1.0	1.0	1.0
Main.main(String[])	7.0	3.0	5.0	5.0
Poly.differentiate()	4.0	1.0	3.0	3.0
Poly.equals(Object)	5.0	3.0	1.0	3.0
Poly.getIndex()	0.0	1.0	1.0	1.0
Poly.merge(Object)	0.0	1.0	1.0	1.0
Poly.Poly(String)	0.0	1.0	1.0	1.0
Poly.toString()	5.0	3.0	3.0	3.0
Term.addFactor(Factor)	3.0	3.0	3.0	3.0
Term.differentiate()	12.0	3.0	7.0	7.0
Term.Term()	0.0	1.0	1.0	1.0
Term.Term(String)	2.0	1.0	1.0	2.0
Term.toString()	7.0	4.0	3.0	5.0
Trig.differentiate()	10.0	1.0	5.0	5.0
Trig.equals(Object)	5.0	3.0	3.0	3.0
Trig.getIndex()	0.0	1.0	1.0	1.0
Trig.getType()	0.0	1.0	1.0	1.0
Trig.merge(Object)	0.0	1.0	1.0	1.0
Trig.reverse(String)	2.0	2.0	1.0	2.0
Trig.toString()	5.0	3.0	3.0	3.0
Trig.Trig(String,String)	0.0	1.0	1.0	1.0
Total	111.0	76.0	91.0	103.0
Average	2.4130434782608696	1.6521739130434783	1.9782608695652173	2.239130434782609

对比上一次作业的改进点：

• 为了能够满足嵌套关系，我把factor定义为抽象类，并且把子类需要的求导和合并方法都定义在其中。

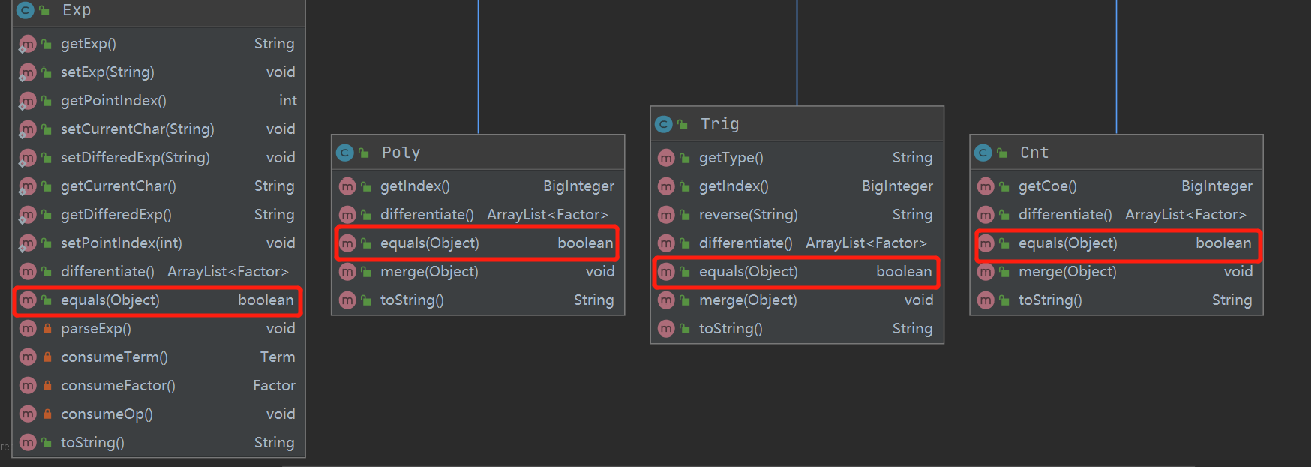
• 并且为了合并的操作，重写了子类的equals方法

算法

递归下降优化：

在理论课上老师吐槽过我们所有方法都public，所有private字段都加set get后，依据面向对象的思想，特意对于修饰符做了一些更改：

通过函数维护一个private static的字符串和下标指针进行递归匹配。

private void advance() {
    Exp.pointIndex += 1;
    if (Exp.pointIndex >= Exp.exp.length()) {
        Exp.currentChar = "#";
    } else {
        Exp.currentChar = String.valueOf(Exp.exp.charAt(Exp.pointIndex));
    }
}

在这里的时候就已经有了“自定义终止符”的想法，这部分在第三次作业中得到了实现。

对于递归下降的parseExp算法，应该是private方法；

删除了大量不必要的get和set方法。

在Exp内设置了多个构造器，以便于重载。

---

这次在读取项和因子的时候，直接使用了while循环代替自身调用，简化了逻辑。

do {
    consumeTerm();
}
while (currentChar.equals("+") || currentChar.equals("-"));

---

依然采用正则辅助匹配factor内容。但是需要注意匹配的顺序。

if (Exp.currentChar.equals("(")) {
    Exp e = new Exp();
    return e;
} //如果匹配到括号应该首先进入到匹配表达式

---

匹配表达式是一个自上而下的过程，从exp开始构造出了整个表达式树。

而求导则是一个自下而上的过程，通过调用exp的求导方法，exp对自己的子类进行调用。而在这时候以父类标签调用子类方法，多态就能发挥作用。

求导方法的最下层应该是poly， trig， cnt中的一个，他们的求导将会返回一个因子的list，上层调用者只需要一边合并list，一边从下而上的构造求导完成后的表达式树即可。

public void addFactor(Factor f) {
    for (Factor factor:factors) {
        if (factor.equals(f)) {
            factor.merge(f);
            return;
        }
    }
    factors.add(f);  //在构造求导树添加节点的同时就合并

优化

• 在化简长度上并没有做到最好，只能合并基本的系数和幂。比如三角函数的恒等式的化简等。
• 其实可以考虑在各个类覆写hashcode方法，用map来存储合并。
• 对于过多的嵌套，不能化简括号，在存储结构上会体现为多重嵌套的单元素list，本人在第二次研讨课上找到了解决方法，这部分在第三次作业讨论。

测评

• 强测和互测都通过了，但是互测中手动构造样例开始变得麻烦。开始研究用simpy和subprocess等模块在python内构造评测机。

• 主要采用随机组合项和正则生成的因子：

  while exp == "":
      exp += x.xeger("x(\\*\\*([+-]{0,1}(0){0,2}[0-9]{1,3})){0,1}")
  return exp
  

• 成功hack到的BUG是在输出表达式时，对于0这种项直接输出了空字符串，导致最后拼接完成直接输出了空串。个人认为这部分问题是在多个类中实现tostring方法时的逻辑出现了混乱，导致没能考虑到各级都传送空串的情况，最后直接输出了。在表达式类的tostring中，应该有判断空串的逻辑，以避免出现空表达式()

第三次作业

类的设计

在第二次作业重构按完成后，第三次作业和第二次作业在我看来差别很小。类的设计基本沿用。

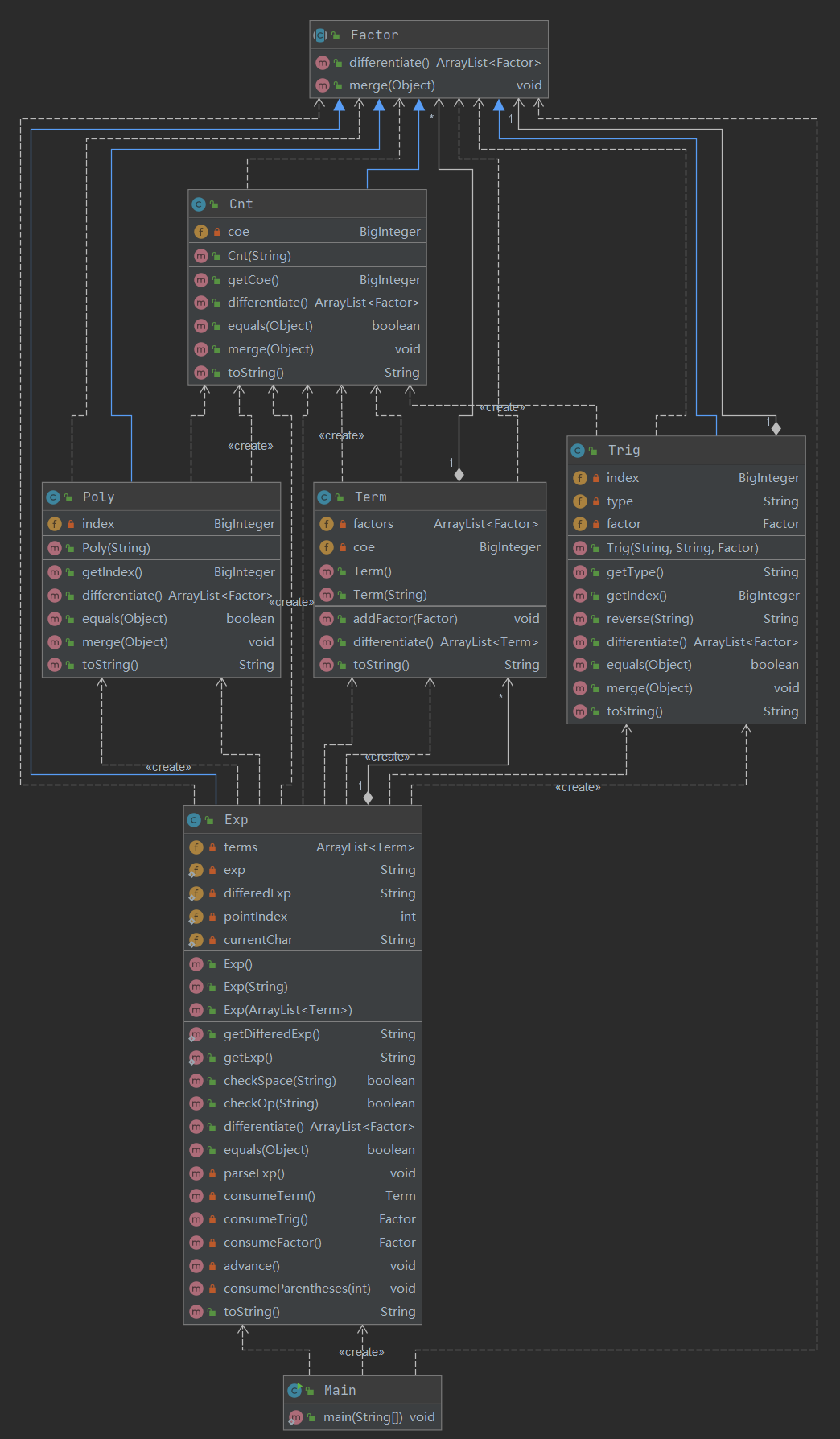
针对于三角函数可以嵌套表达式的情况，调整了类的结构，在三角函数内放置了因子数据段。

方法度量：

Method	CogC	ev(G)	iv(G)	v(G)
Cnt.Cnt(String)	0.0	1.0	1.0	1.0
Cnt.differentiate()	0.0	1.0	1.0	1.0
Cnt.equals(Object)	5.0	3.0	1.0	3.0
Cnt.getCoe()	0.0	1.0	1.0	1.0
Cnt.merge(Object)	0.0	1.0	1.0	1.0
Cnt.toString()	0.0	1.0	1.0	1.0
Exp.advance()	2.0	1.0	2.0	2.0
Exp.checkOp(String)	1.0	2.0	1.0	2.0
Exp.checkSpace(String)	18.0	10.0	6.0	12.0
Exp.consumeFactor()	16.0	6.0	6.0	9.0
Exp.consumeParentheses(int)	7.0	1.0	5.0	5.0
Exp.consumeTerm()	9.0	3.0	6.0	6.0
Exp.consumeTrig()	20.0	4.0	6.0	7.0
Exp.differentiate()	1.0	1.0	2.0	2.0
Exp.equals(Object)	0.0	1.0	1.0	1.0
Exp.Exp()	0.0	1.0	1.0	1.0
Exp.Exp(ArrayList)	0.0	1.0	1.0	1.0
Exp.Exp(String)	13.0	1.0	4.0	5.0
Exp.getDifferedExp()	0.0	1.0	1.0	1.0
Exp.getExp()	0.0	1.0	1.0	1.0
Exp.parseExp()	2.0	1.0	3.0	3.0
Exp.toString()	6.0	3.0	3.0	6.0
Factor.differentiate()	0.0	1.0	1.0	1.0
Factor.merge(Object)	0.0	1.0	1.0	1.0
Main.main(String[])	13.0	4.0	6.0	6.0
Poly.differentiate()	4.0	1.0	3.0	3.0
Poly.equals(Object)	5.0	3.0	1.0	3.0
Poly.getIndex()	0.0	1.0	1.0	1.0
Poly.merge(Object)	0.0	1.0	1.0	1.0
Poly.Poly(String)	0.0	1.0	1.0	1.0
Poly.toString()	5.0	3.0	3.0	3.0
Term.addFactor(Factor)	3.0	3.0	3.0	3.0
Term.differentiate()	12.0	3.0	7.0	7.0
Term.Term()	0.0	1.0	1.0	1.0
Term.Term(String)	2.0	1.0	1.0	2.0
Term.toString()	7.0	4.0	3.0	5.0
Trig.differentiate()	1.0	1.0	2.0	2.0
Trig.equals(Object)	0.0	1.0	1.0	1.0
Trig.getIndex()	0.0	1.0	1.0	1.0
Trig.getType()	0.0	1.0	1.0	1.0
Trig.merge(Object)	0.0	1.0	1.0	1.0
Trig.reverse(String)	2.0	2.0	1.0	2.0
Trig.toString()	5.0	3.0	3.0	3.0
Trig.Trig(String,String,Factor)	0.0	1.0	1.0	1.0
Total	159.0	85.0	99.0	122.0
Average	3.6136363636363638	1.9318181818181819	2.25	2.772727272727273

主要修改的部分有递归下降的部分，配合了内置的终结符检测非法情况，同时要修改了三角函数的求导和toString方法。

仍然存在正则

在第二次作业重构按完成后，第三次作业和第二次作业在我看来差别很小。类的设计基本沿用。

对于大部分用递归下降的同学来说，他们可能会直接完全按表达式形式化表述来写递归下降。一度有正则无用，却还被挂在课程指导书里之类的吐槽。

但是本人对于递归下降的实现并不拘泥于死板的依赖表达式形式化表述。从第一次作业开始，我就指出应该可以根据条件，利用正则辅助递归下降。

总体来说这种辅助无外乎： 匹配去掉所有空白符，去掉连续符号，匹配因子。

在第三次作业中，我可能的思考如何把他打回到第二次作业里，这样就可以修改尽可能少的代码。

仔细阅读所谓新增的语法检查的要求，再回头看看我们希望正则能帮上忙的地方，其实只要这样写：

• 用正则搜索在**之间的空白符
• 搜索sin cos关键字的空白符
• 搜索有符号整数符号和数字之间的空白符
• 搜索数字之间的空白符

找到就报错，检测完成后直接消除所有空白符。

if (!checkSpace(exp)) {
    Exp.exp = "WRONG FORMAT!";
} else {

然后正则查找符号序列，符号序列的长度如果大于3，报错，否则消去符号到一个。

至此，剩下的部分就完全可以沿用第二次的递归下降算法。

当然，这种方法其实更像是分类讨论， 讨论成功与否在于分类是否全面，他可以说是对形式化表述的进一步抽象得出的结论。

内置的关键字？

还记得刚才在第二次作业用advance()函数来维护指针的时候，对于超过表达式长度的下标，我把当前字符设置成了#

其实我们可以定义多种多样的内置字符来表达不同含义，只要我们事先检验这些字符是否在表达式内，一般这些都是表达式的非法字符，有则报错，没有的话我们就可以把当前字符设置成我们想要的字符，用作我们程序的“关键字”

在我的程序中我用#表示递归下降正常结束，而用!来表示了非法。

if ((new BigInteger(m.group("index")))
        .abs().compareTo(new BigInteger("50")) > 0) {
    Exp.currentChar = "!";
}

优化

• 之前提到过我在第二次研讨课上找到了优化多层单元素嵌套的方法：

那就是从一开始递归下降匹配表达式的时候就优化他的存储结构。
应该在每次当遇到单元素的情况时，直接向下调用，而不是先去new一个对象再去用对象调用匹配。
如果可以的话完全可以利用工厂模式做这一部分的优化，只需要嵌套调用工厂即可。

• 第二点是个人使用多态时候的一些思考：

方法应该也可以在多态的时候重载，所以可以选择在抽象类或者接口里多写一个重载方法。这样在设计时输入的参数就可以比较灵活。

评测

首先是令人出乎意料的是Integer.parserInt的弱小，虽然这不太像是第三次作业该出现的问题，但是这位函数在解析大数字时候直接会报错，只能说自己迷迷糊糊就直接选了这个函数用于判断指数绝对值不大于50，也许是BigInteger让我产生了所有函数都能解析大数的错觉 XD。

其次就要回到刚才讨论的正则辅助的问题了，我提到过讨论不全面就会存在BUG的问题，显然这次做的还是略显仓促，没有做充分的验证，对于有符号整数的讨论漏掉了一个情况。

只要补充一下对应的正则和判断逻辑就可以了。

regex = "(?<=(sin\\()|(cos\\())([\\+-]+)(\\s+)(\\d+)";
.....

心得体会

通过第一单元的作业，对于面向对象的设计思路有了进一步理解，在写代码前能够提前思考，设计父类和接口，运用方法重载、多态和工厂类。虽然程序本身还有浓厚的面向过程的逻辑，但是在第二次到第三次作业只用微小调整类的结构和方法就完成了功能拓展，相比于面向过程的程序，面向对象明显增加了代码复用度和可拓展性。当然，最佳的设计更应该能完成模块之间的解耦，在这一点自己的设计上还需要继续精进。