离散数学期中总结
命题逻辑
命题表达式
$p\bigvee q,p\bigwedge q,$
$p\rightarrow q=\neg{p}\bigvee q=\neg{q}\rightarrow\neg{p}$,
其真值表如下: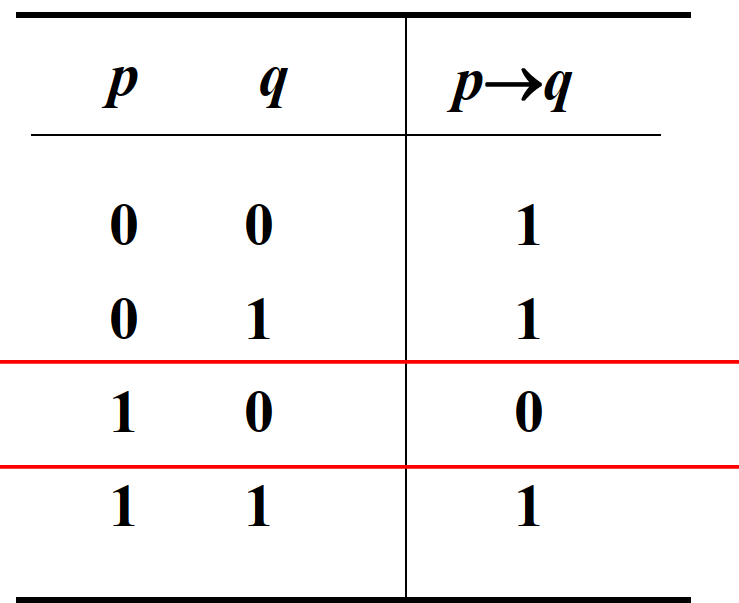
$p\leftrightarrow q=(p\rightarrow q)\bigwedge(q\rightarrow p)$
其真值表如下: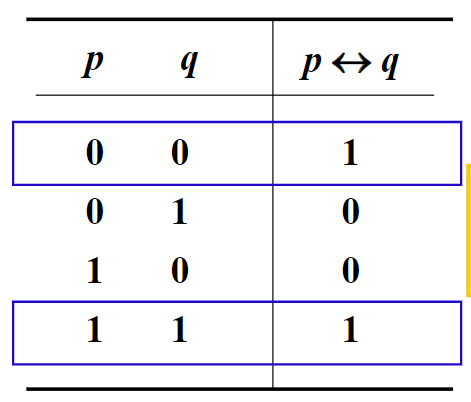
运算符优先级:$\neg>\bigwedge>\bigvee>\rightarrow>\leftrightarrow$
将自然语言翻译成命题表达式
一个例子:
命题表达式的真值表以及永真式、矛盾式与可能式
逻辑等价

常用的逻辑等价
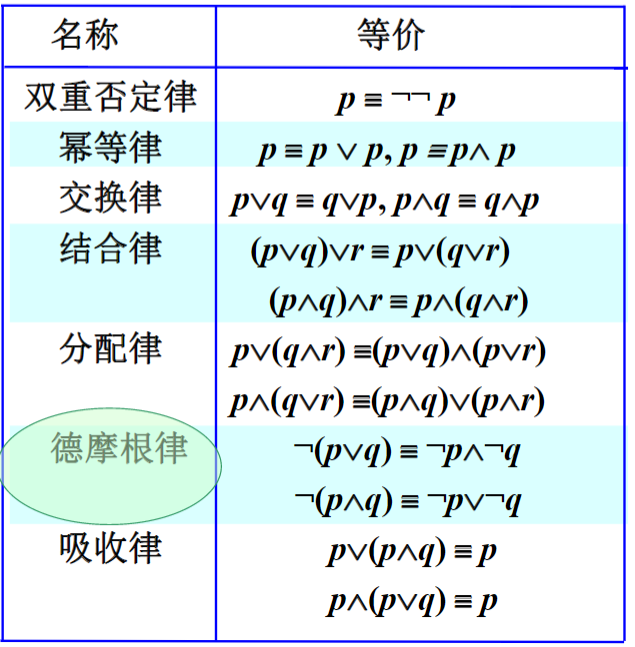
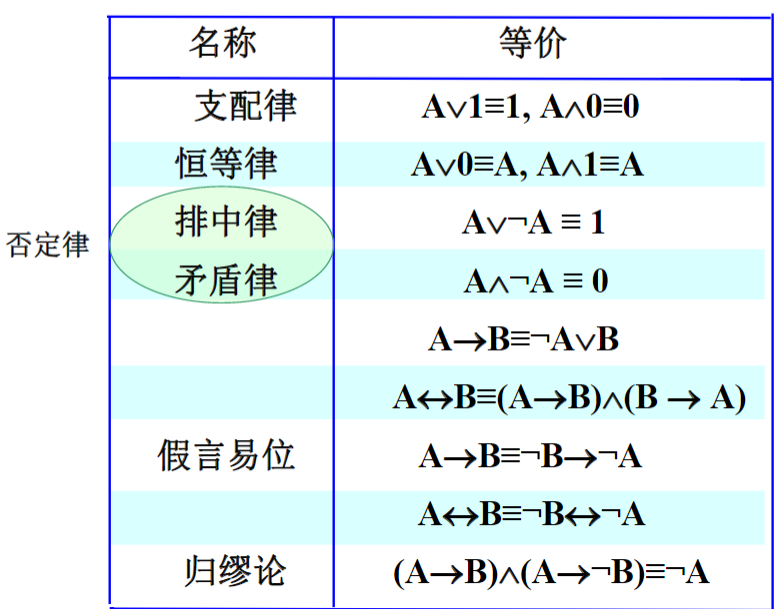
命题逻辑公式的范式
- 包含所有命题变元或其否定一次仅一次的简单合取式($\land$),称为极小项;
- 包含所有命题变元或其否定一次仅一次的简单析取式($\lor$),称为极大项;
- 由有限个极小项组成的析取范式称为主析取范式(和式$\lor$);
- 由有限个极大项组成的合取范式称为主合取范式(积式$\land$)。
命题逻辑的“自然演绎”规则

谓词逻辑及自然语言的翻译


注意:


例子:
1.

2.

注意:全称量词一般用蕴含$\rightarrow$,存在量词一般用合取$\land$(因为若条件为假,则语句为真,此时可能对)
证明方法




集合及其运算
- 幂集:
![img]() , 若$|A|=n$,则$|P(A)|=2^n$
, 若$|A|=n$,则$|P(A)|=2^n$ - 集合的运算:交,并,补
![img]() ,
,
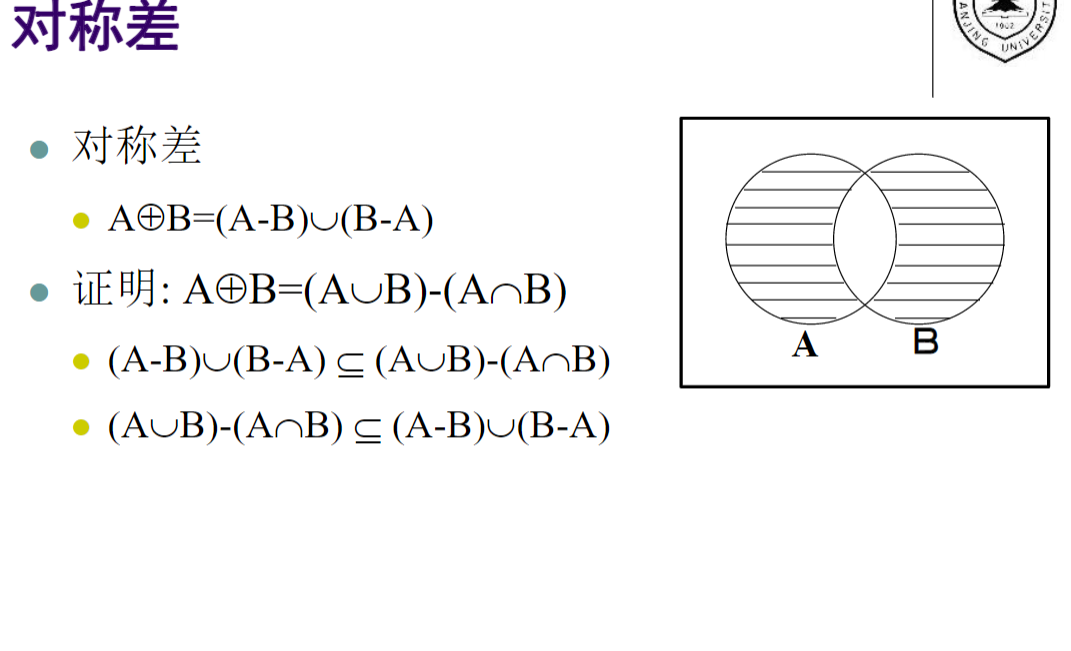
对称差:![img]()
性质:![img]()
![img]()
- 自然数的定义:
![img]()
- 特殊例子:
![img]()
![img]()
- 笛卡尔积:
![img]()
- 集合等式的证明:
![img]()
![img]()
![img]()
关系及其运算
- 特殊的关系:
![img]()
- 关系的运算:
![img]()
![img]()
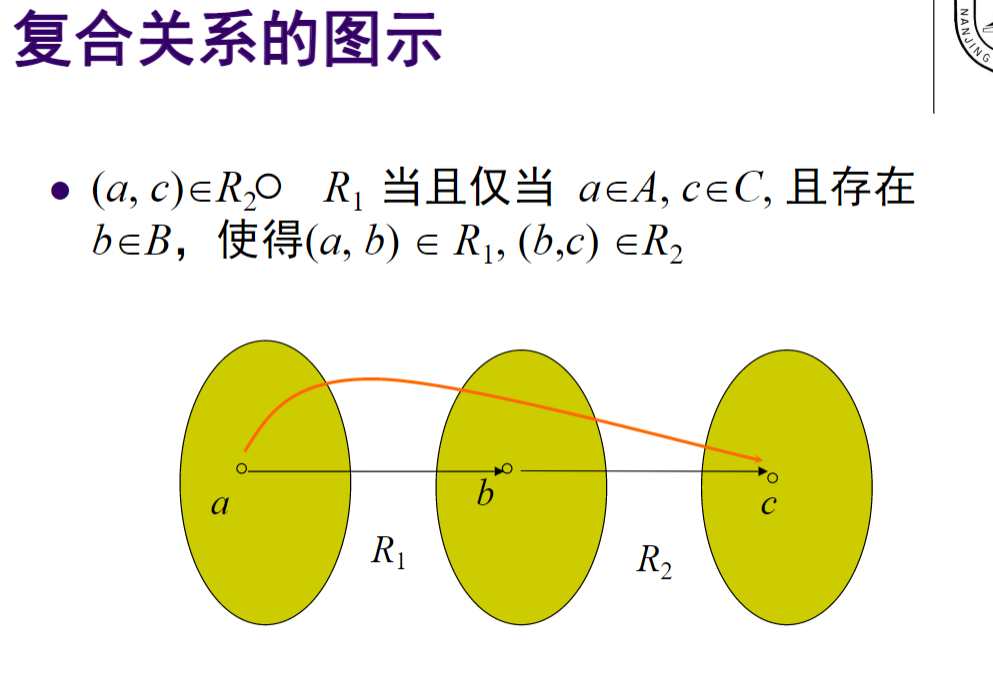
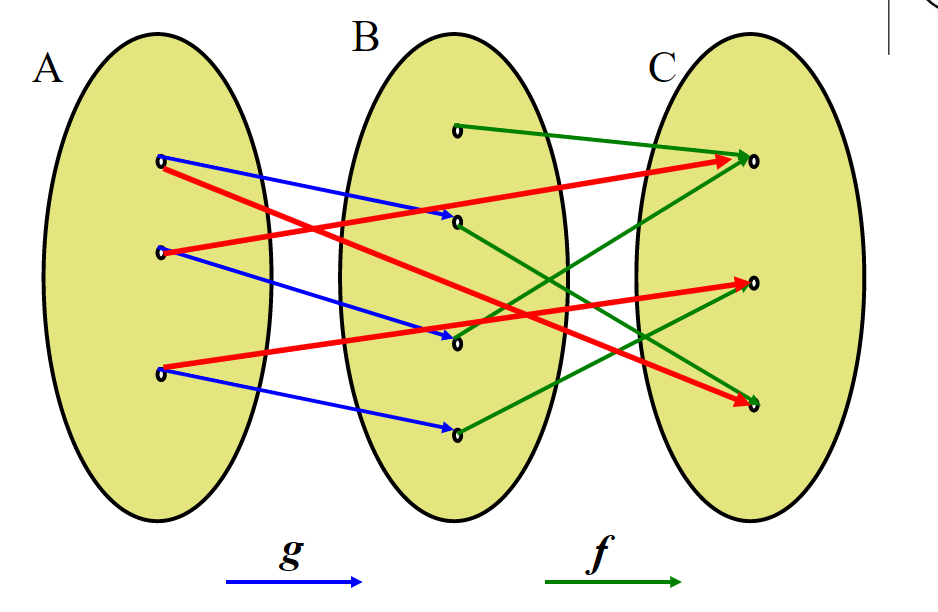
重点: 关系的复合:![img]()
![img]()
![img]()
![img]()
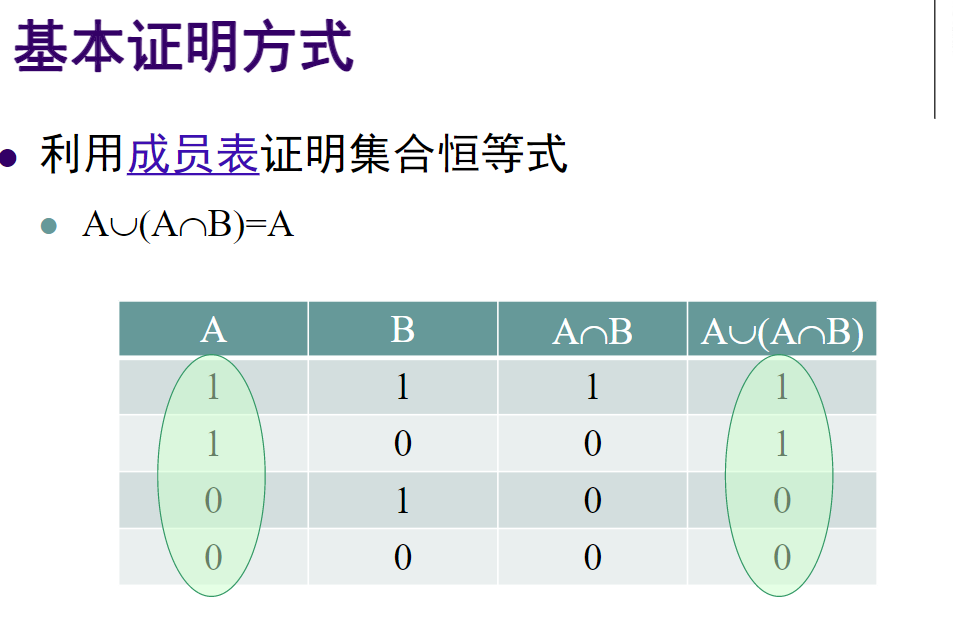
- 0-1矩阵运算(成员表):
![img]()
![img]()
- 关系的性质:
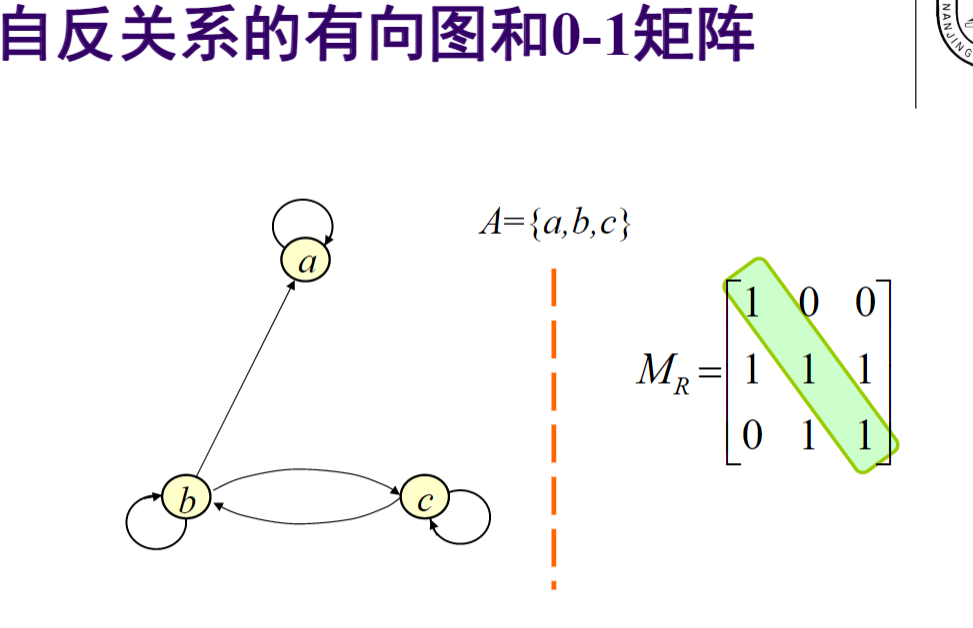
- 自反性:注意自反(对$\forall a\in A$),反自反,非自反的关系
![img]()
![img]()
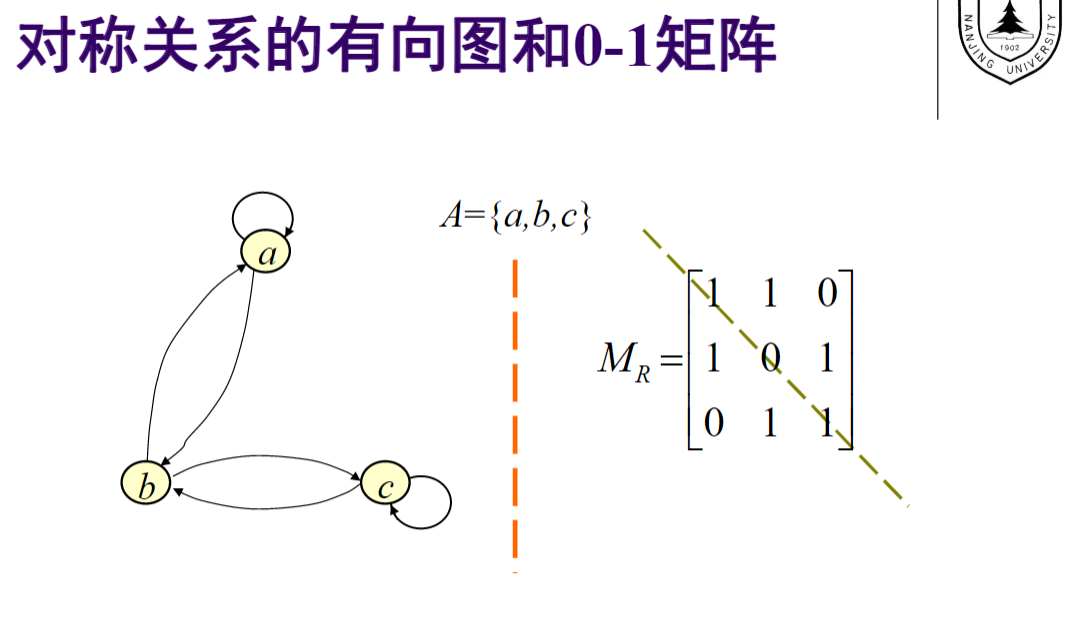
- :
![img]()
![img]() :前提不满足,则后续不用证明,结论为真
:前提不满足,则后续不用证明,结论为真
![img]()
![img]()
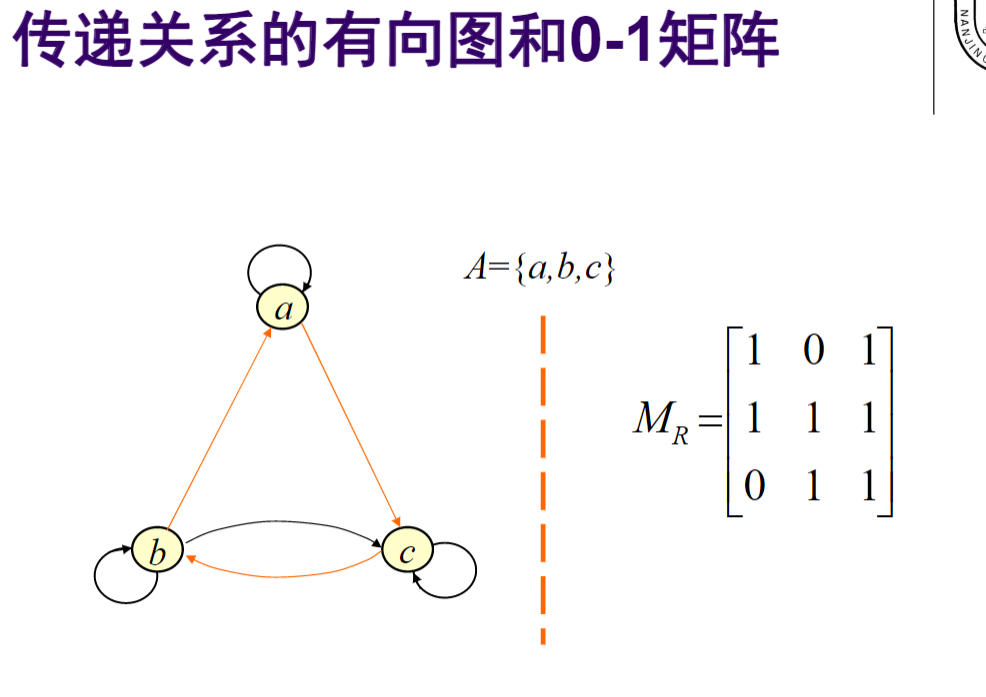
- 传递性:
![img]()
![img]()
![img]()
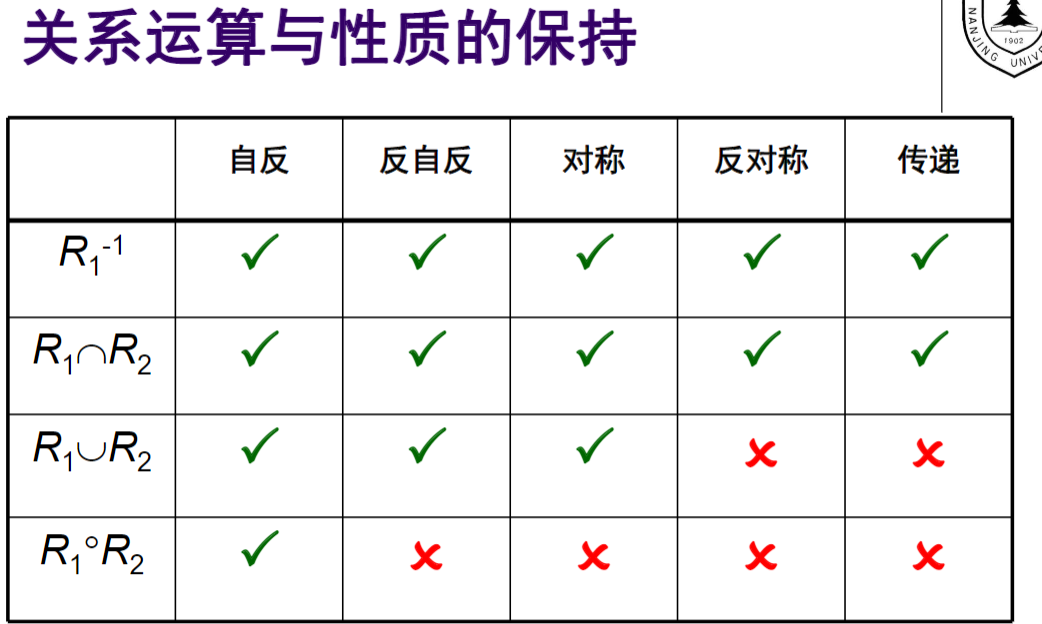
- 关系的运算与性质的保持:
![img]()
函数及其运算
- 定义:定义域,伴域,值域,像,原像
![img]()
- 定义:$B^A$
![img]()
![img]()
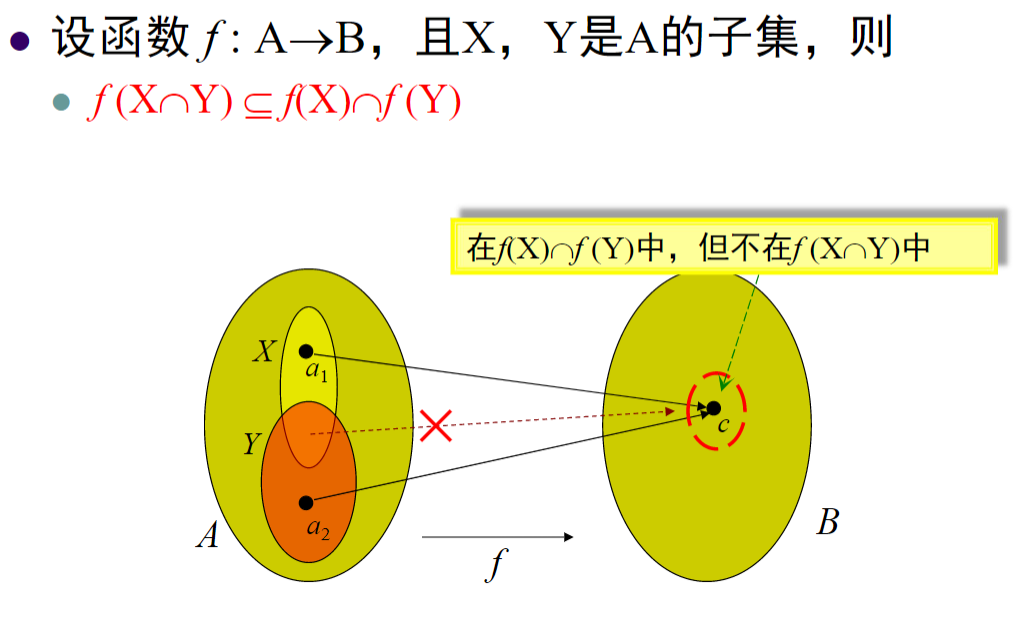
- 并集,交集的关系:
![img]()
![img]()
- 函数性质:
![img]()
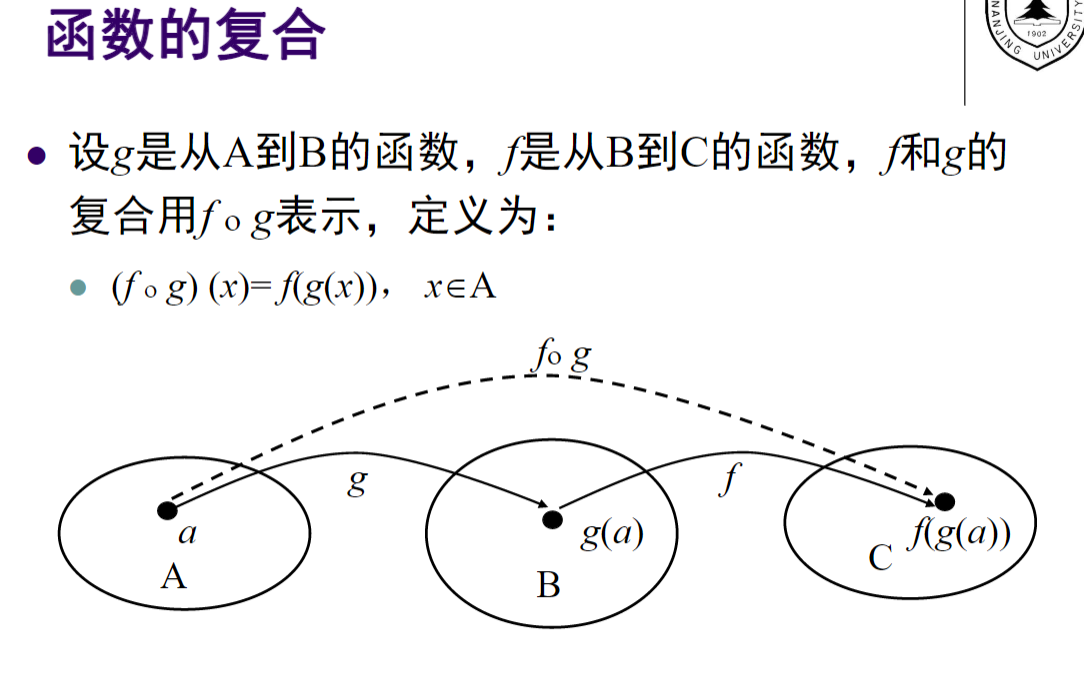
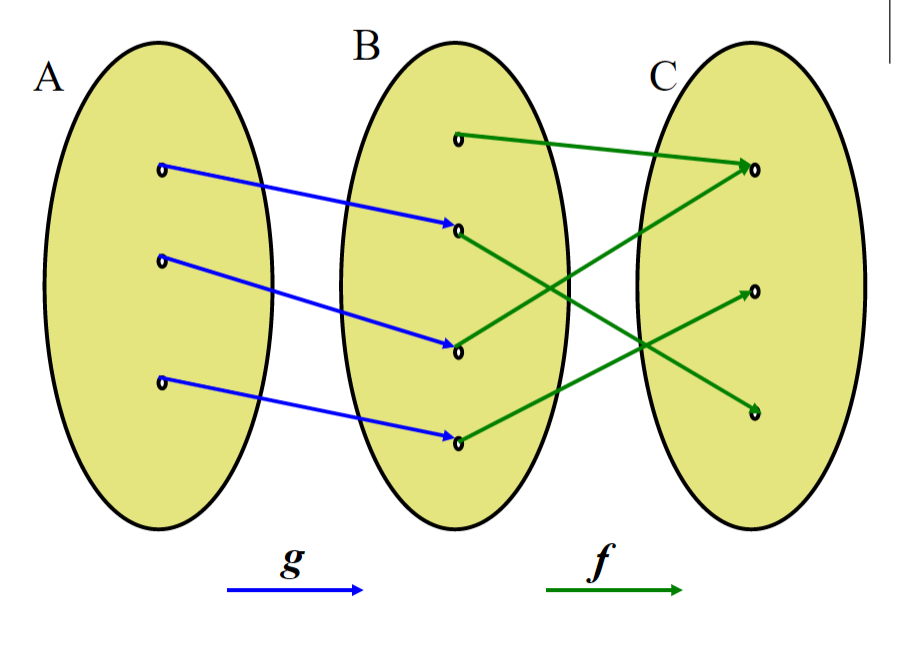
- 反函数,函数的复合:
![img]()
![img]()
![img]()
满射证明:![img]()
单射证明:![img]()
关系闭包和等价
- 定义:
![img]()
包含关系R,满足性质P的最小关系 - 自反闭包:
- 定义:
![img]()
- 计算公式:
![img]()
- 对称闭包:
- 计算公式:
![img]()
- 传递闭包:
- 连通关系:
![img]()
$R^*$即为对存在通路的元素$a,b$ ($a\rightarrow t_1,t_1\rightarrow t_2,···,\rightarrow b$) ,搭桥:$a\rightarrow b$,因此满足传递性 - 计算公式:
![img]()
- 有限集合上的传递闭包:
![img]()
- 定义证明闭包性质:
![img]()
![img]()
- Warshall算法求传递闭包:
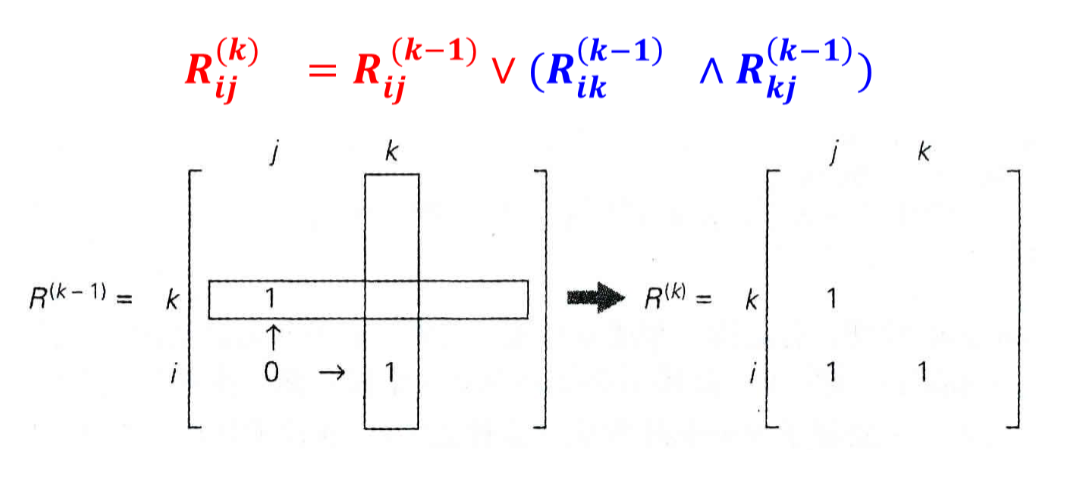
- 公式:
![img]()
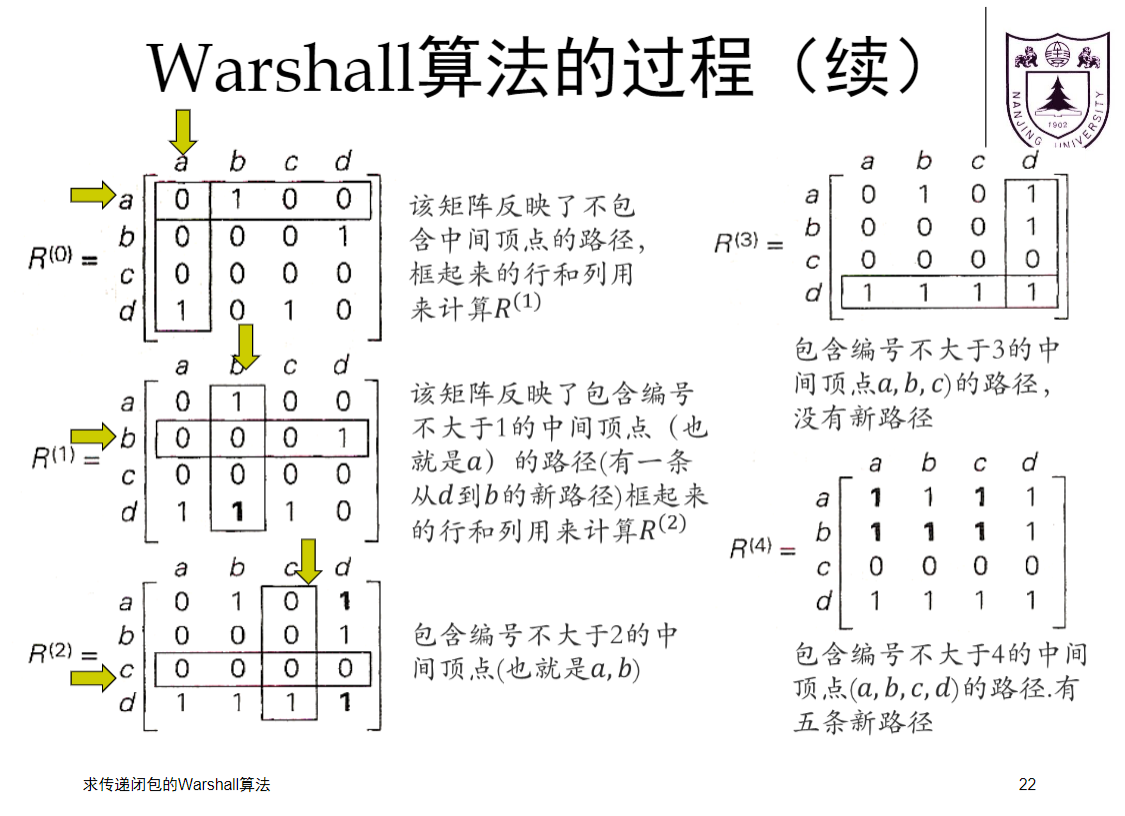
- 过程:
![img]()
- 按对角线圈出第i行i列,
- 由该列中的1计算出除i行i列外的1
- 等价关系:
![img]()
- 等价类:
- 定义:
![img]()
- 代表元素:
![img]()
- 商集:
![img]()
对A的划分:![img]()
例子:![img]()
![img]()
偏序和偏序格
- 偏序关系定义:
![img]()
例子:![img]()
- 可比,全序,覆盖定义:
![img]()
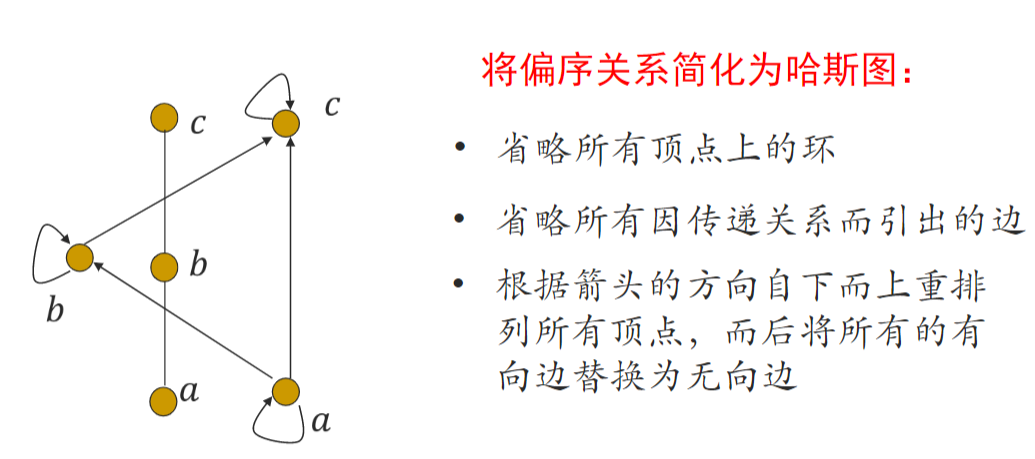
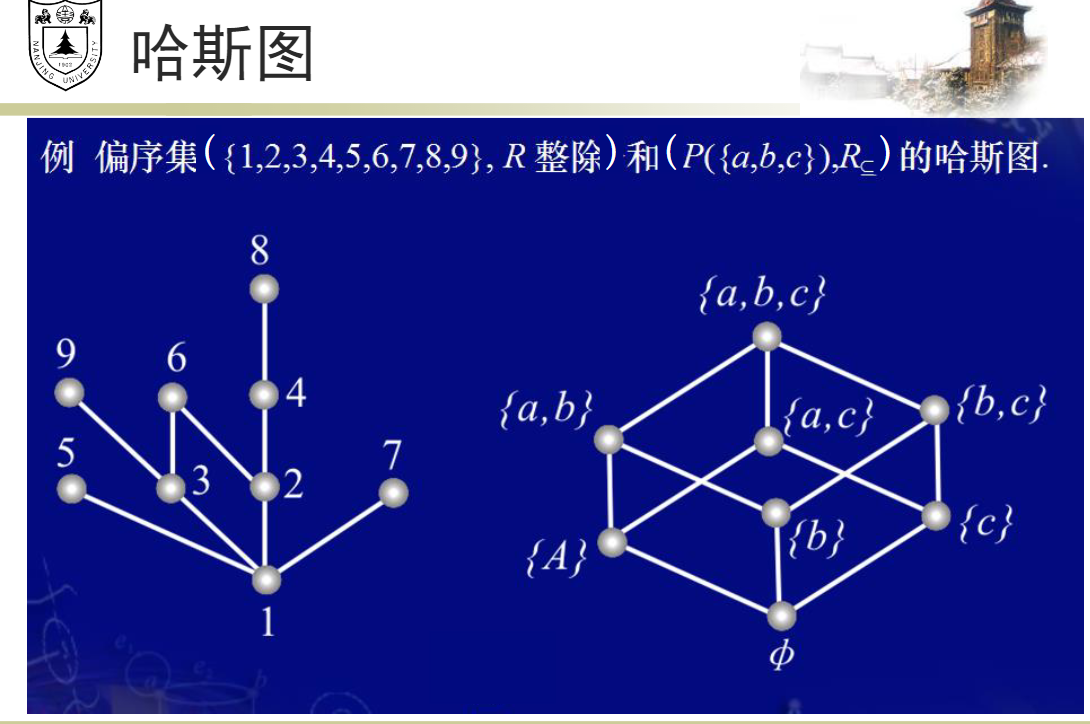
- 偏序集和哈斯图:
![img]()
例子:![img]()
![img]()
- 偏序集中特殊元素及性质:
![img]()
![img]() 上,下界需为共同交点元素
上,下界需为共同交点元素
图示:![img]()
![img]()
例子:![img]()
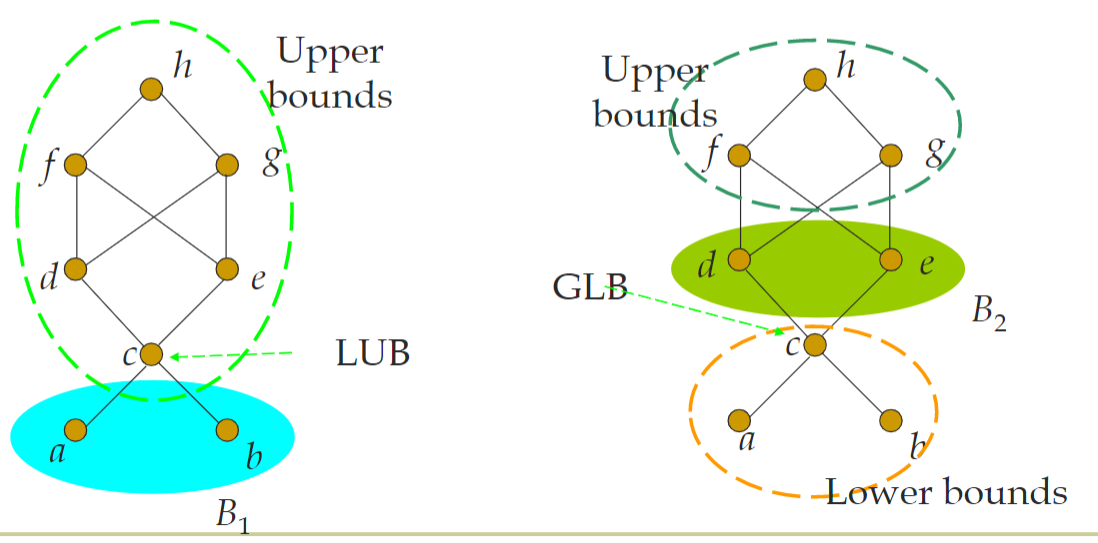
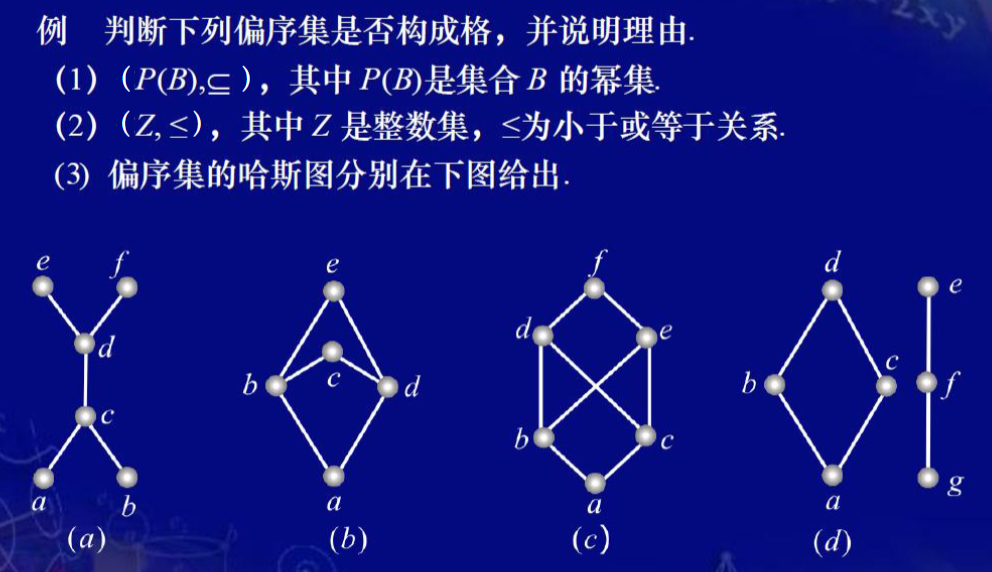
- 格:
- 定义:
![img]() 任意两个元素均有上下确界,并重新定义了$\land,\lor$
任意两个元素均有上下确界,并重新定义了$\land,\lor$ - 例子:
![img]()
![img]()
- 对偶定理
![img]()
![img]()
集合的基数
-
等势关系定义:
![img]()
-
可列集:
![img]()
特别的:可列个可列集的并集,笛卡尔积仍然是可列集合 -
可数集:有限的或与自然数集等势的集合
-
有限与无限集:
![img]()
- 一个例子:
![img]()
- 康托尔定理:
![img]()
- 集合的优势关系:
![img]()
![img]()
性质:![img]()
一个例子:![img]()
等势关系R=对应的双射f,元素为集合![img]()
- 集合的基数:
![img]()
一个例子:康托对角线法---![img]()
![img]()
另一个例子:![img]() 其中${0,1}^N$表示N中元素是否存在的所有可能的集合,即可代表N的幂集
其中${0,1}^N$表示N中元素是否存在的所有可能的集合,即可代表N的幂集
数论初步
- 模的基本性质:
![img]()
- 最大公约数:
- 定义:
![img]()
- 性质:
![img]()
- 第一条性质(贝祖定理)的证明:
![img]()
- 算术基本定理:
![img]()
- 欧拉函数与欧拉定理:
- 欧拉函数:
![img]()
- 欧拉定理与费马小定理:
![img]()
![img]()
归纳与递归
- 数学归纳法:
![img]()
良序公理:正整数集合的非空子集都有一个最小元素 - 强数学归纳法:
![img]()
良序公理证明:![img]()
- 递归定义:
![img]()
- 结构归纳法:
![img]()
计数
- 容斥原理:
![img]()
- 错位排序:
![img]()
![img]()
![img]()
- 鸽笼原理:
![img]()
一般的:![img]()
特殊例子:![img]()
![img]()
- 排列组合:隔板法,特殊值法,全排和选择
- 二项式定理:赋值法,展开法,
![img]()
离散概率
- 基于集合论的定义:
![img]()
![img]()
- 条件概率:
![img]()
- 贝叶斯定理:
![img]()
例子:![img]()
![img]()
![img]()
- 事件独立性:
![img]()
- 随机变量:
![img]()
例子:![img]()
- 期望:
![img]()
例子:![img]()
条件期望:![img]()
期望的线性性:![img]()
例子:![img]()
独立随机变量的期望:![img]()
- 方差:
![img]()
另一个计算公式:$V(X)=E(X2)-E(X)2$
例子:![img]()
性质:![img]()
PS:各种期望计算公式:![img]()
二项分布:X~B(n,p),X可能发生,可能不发生,发生的概率为p,则$E(X)=np,D(X)=np(1-p)$;
几何分布:在$n$次实验中,前$k-1$次均失败,第$k$次成功的概率,其中每次成功的概率为$p$,则该概率为$p_k=(1-p){k-1}p$,期望为$E(x)=\frac{1}{p}$,方差为$D(x)=\frac{1-p}{p2}$;
超几何分布:考虑$N=N_1+N_2$个外表相同的物品,其中有$N_1$个同类物品与另一类的$N_2$个物品(次品);抽取$n$个物品,每个物品的抽取等概率随机。
则抽取到x个$N_1$物品的概率为:$P(X)=\frac{C{,x}_{N_1}*C_{N_1}}{C^{,n}_N}$,期望为$E(X)=n\frac{N_1}{N}$,方差为:$D(X)=n\frac{N_1}{N}\frac{N_2}{N}*\frac{N-n}{N-1}$;



 , 若$|A|=n$,则$|P(A)|=2^n$
, 若$|A|=n$,则$|P(A)|=2^n$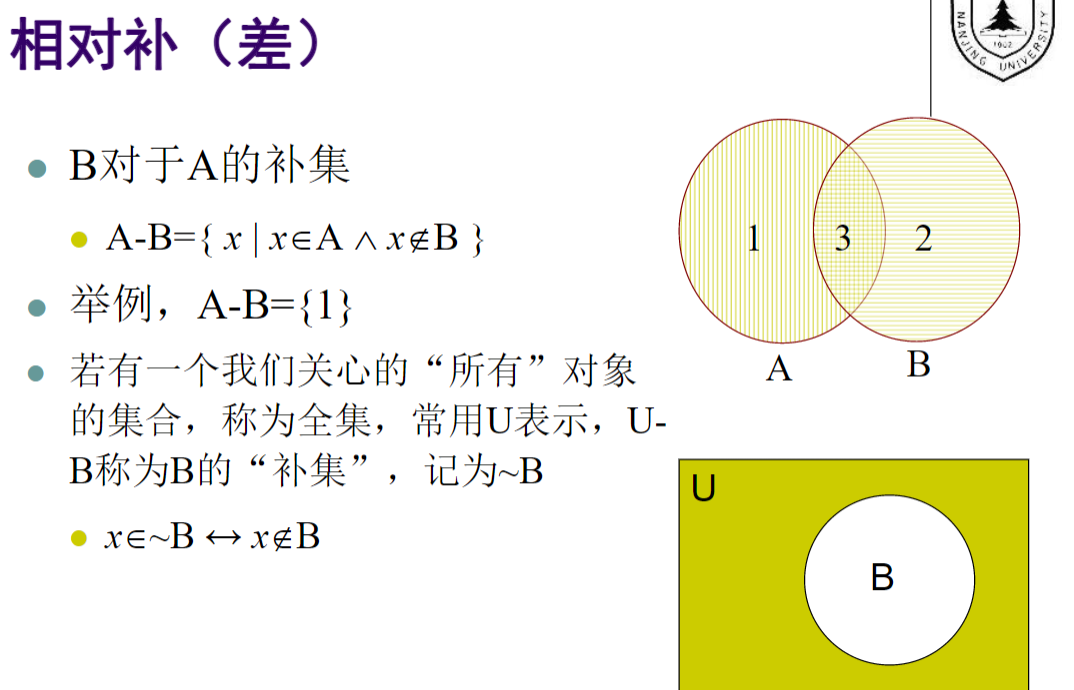 ,
,















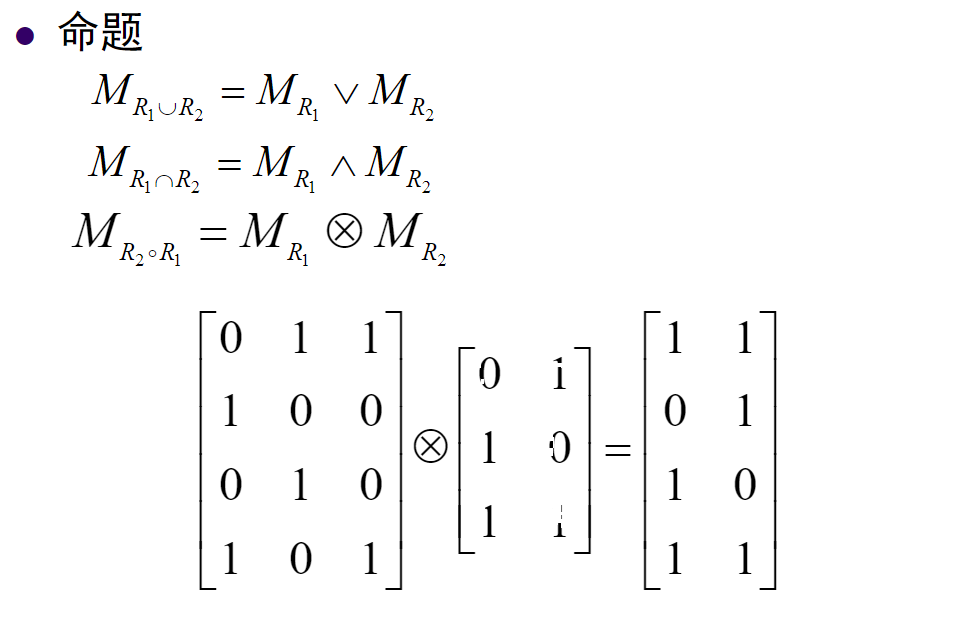


 :前提不满足,则后续不用证明,结论为真
:前提不满足,则后续不用证明,结论为真






























 上,下界需为共同交点元素
上,下界需为共同交点元素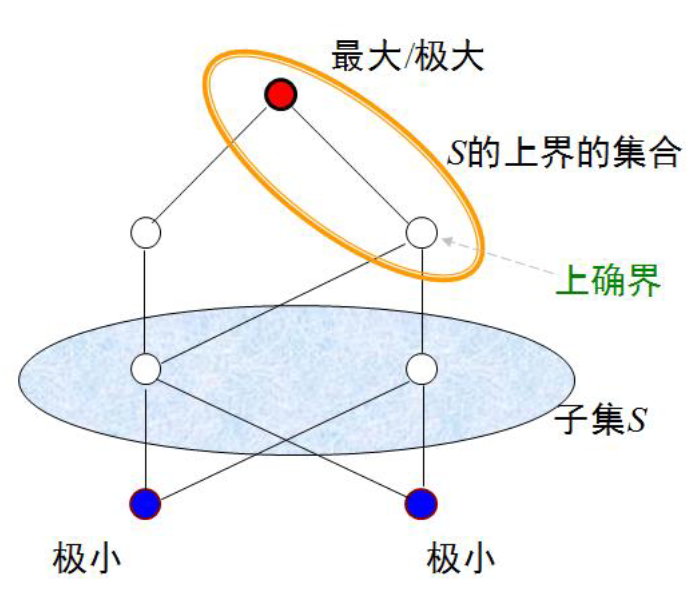

 任意两个元素均有上下确界,并重新定义了$\land,\lor$
任意两个元素均有上下确界,并重新定义了$\land,\lor$















 其中${0,1}^N$表示N中元素是否存在的所有可能的集合,即可代表N的幂集
其中${0,1}^N$表示N中元素是否存在的所有可能的集合,即可代表N的幂集




















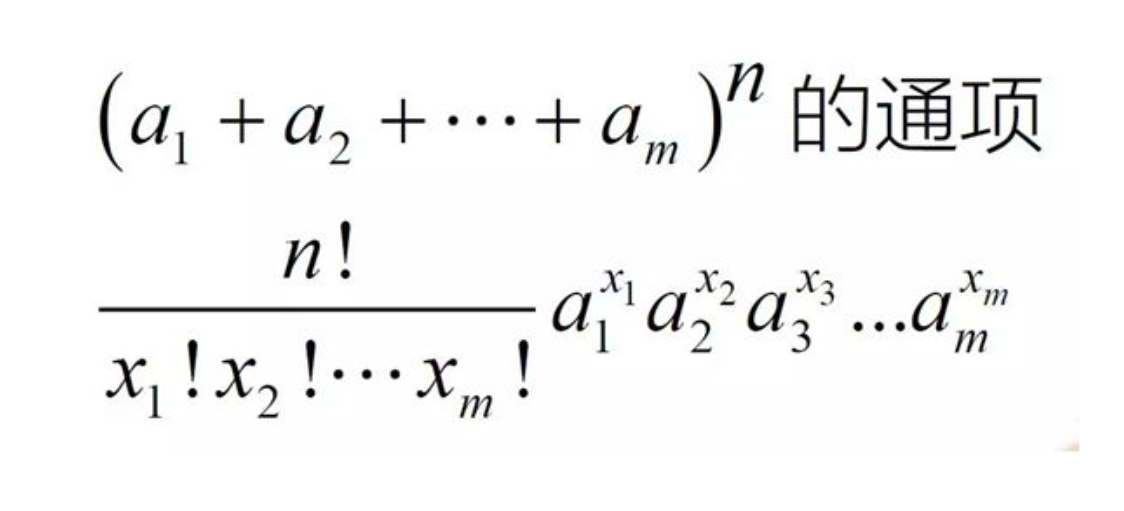





















 浙公网安备 33010602011771号
浙公网安备 33010602011771号