多视图子空间聚类/表示学习(Multi-view Subspace Clustering/Representation Learning)
作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
- “横看成岭侧成峰，远近高低各不同。”多视图聚类是最近一个较为热门的研究话题。这篇博文主要对张长青团队的五篇文章(1)"Low-Rank Tensor Constrained Multiview Subspace Clustering"(2015 ICCV)，(2)"Tensorized Multi-view Subspace Representation Learning"(2020 IJCV)，(3)"Latent Multi-view Subspace Clustering"(2017 CVPR)，(4)"Generalized Latent Multi-View Subspace Clustering"(2020 TPAMI)和(5)"Consistent and Specific Multi-View Subspace Clustering"(2018 AAAI)的算法进行介绍。由于第三篇文章是第四篇文章中的一部分内容(线性部分)，因此第三篇文章直接参看"Generalized Latent Multi-View Subspace Clustering"中的前半部分内容即可。
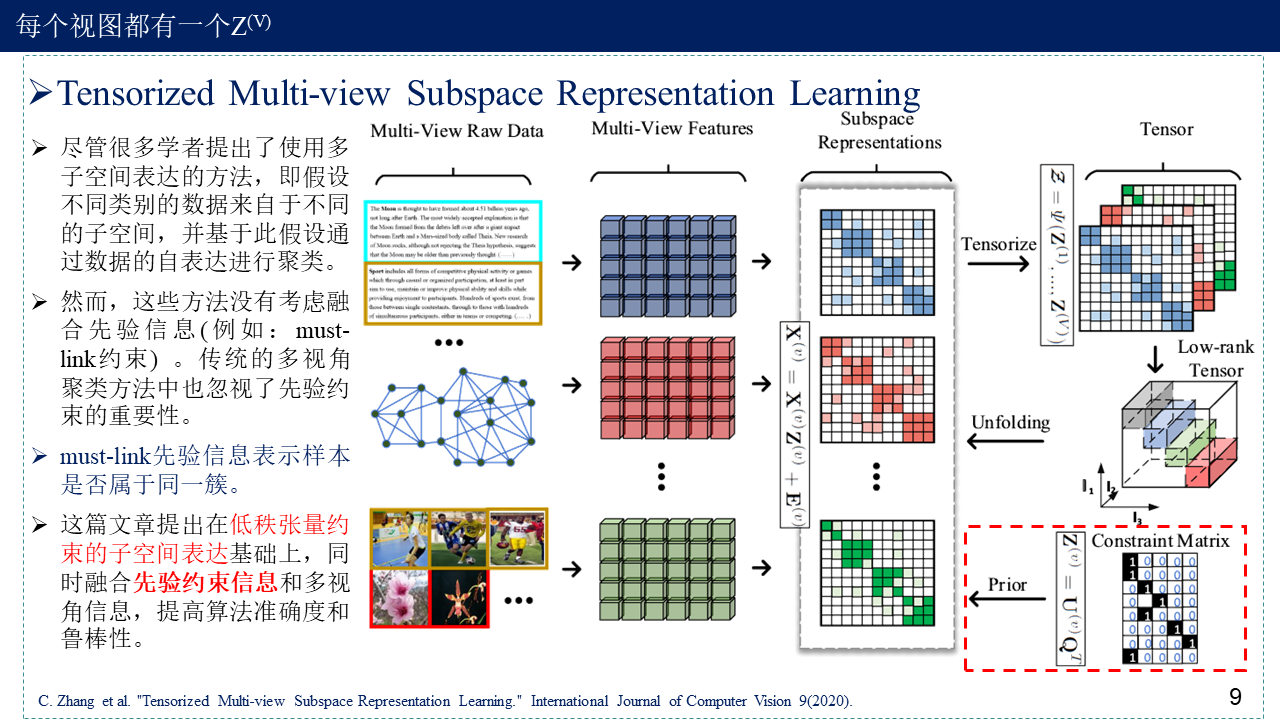
- 第一篇文章主要是将低秩张量约束引入到了多视角子空间聚类，联合地学习各视角的子空间表达以同时挖掘视角内及视角间的高阶关联信息。
- 第二篇文章在第一篇文章的基础上，引入先验信息，可能是监督信息，来学习子空间表示，用于分类任务，如果先验信息没有的话，该方法就退化为第一篇文章的算法，用于无监督聚类任务。
- 而第三和第四篇文章主要是假设多个视图共享同一个公共子空间表示Z，而不是每个视图都有一个各自的子空间表示。第三篇是线性映射，第四篇新增了一个非线性映射，引入神经网络进行非线性映射，来学习公共的潜在表示H。
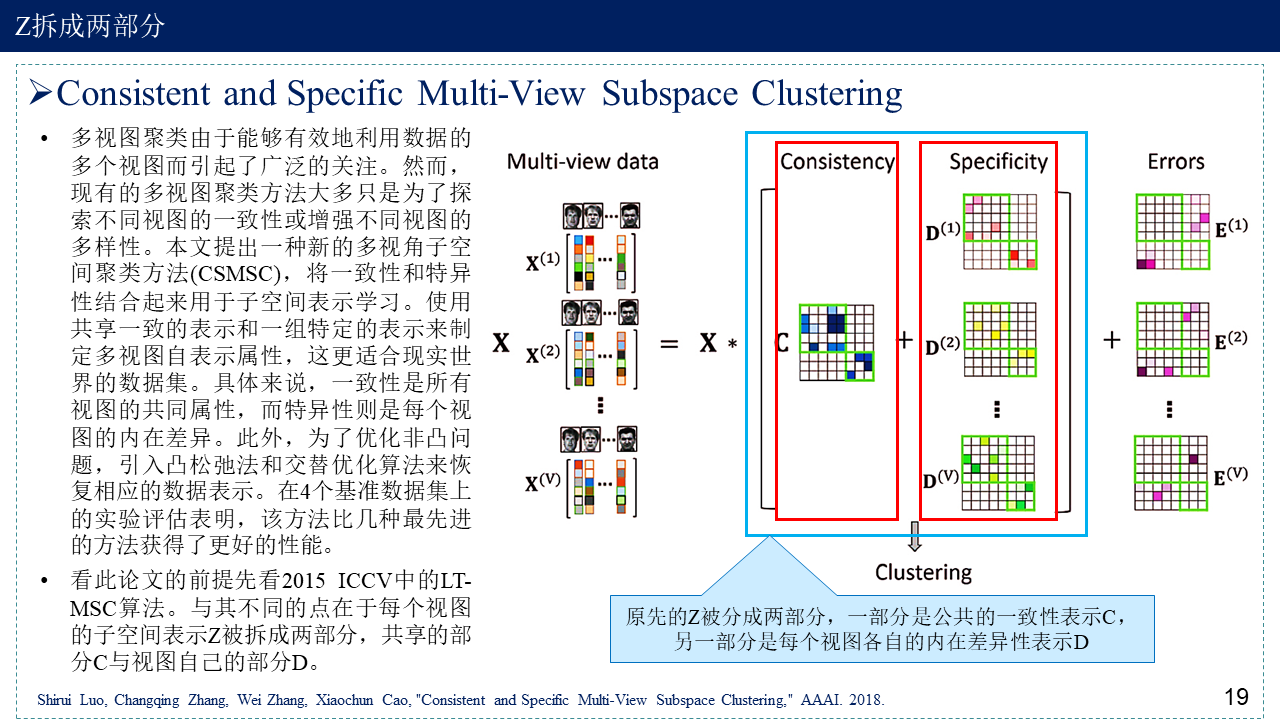
- 第五篇文章是在第一篇文章的基础上将每个视图的Z拆成两部分，一部分为视图共享的表示C，一部分为每个视图各自的差异性表示D。
- 多视图子空间聚类主要思想是通过某些算法得到子空间表示(可以是每个视图各自的，也可以是一个公共的)Z，然后构造相似度矩阵S，最后利用谱聚类算法来得到最终的聚类结果。
1. 基础知识
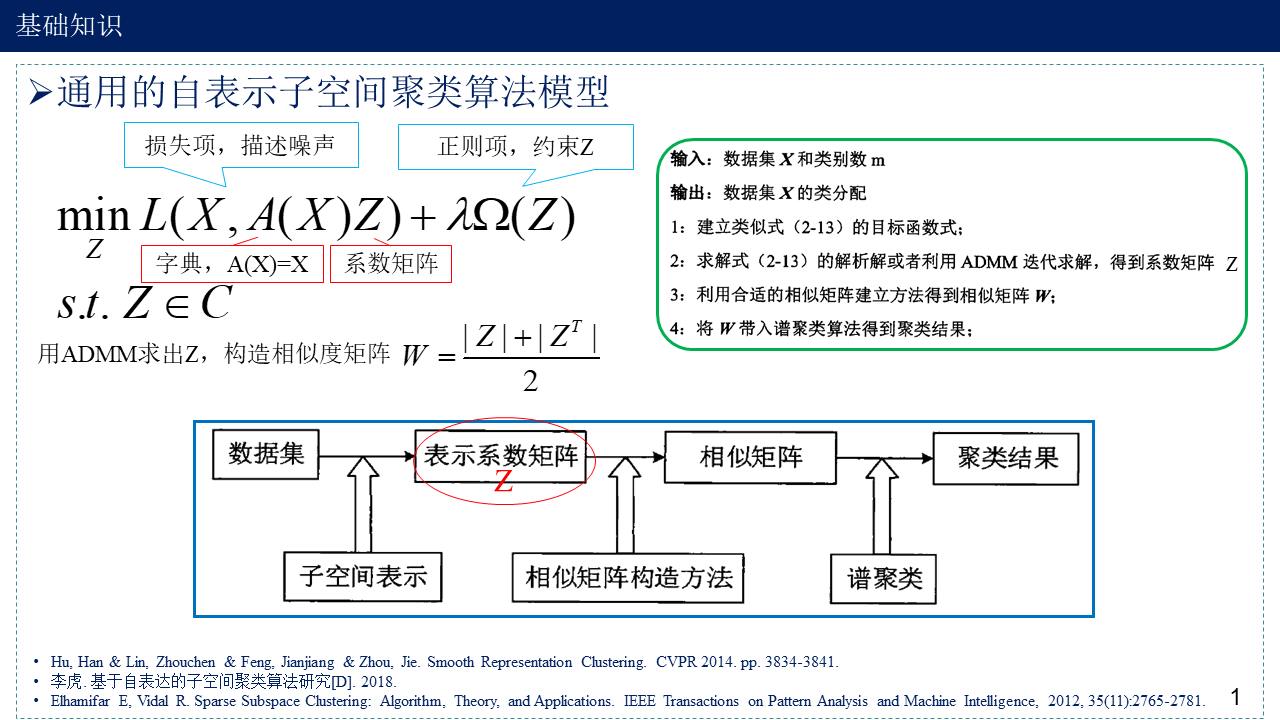
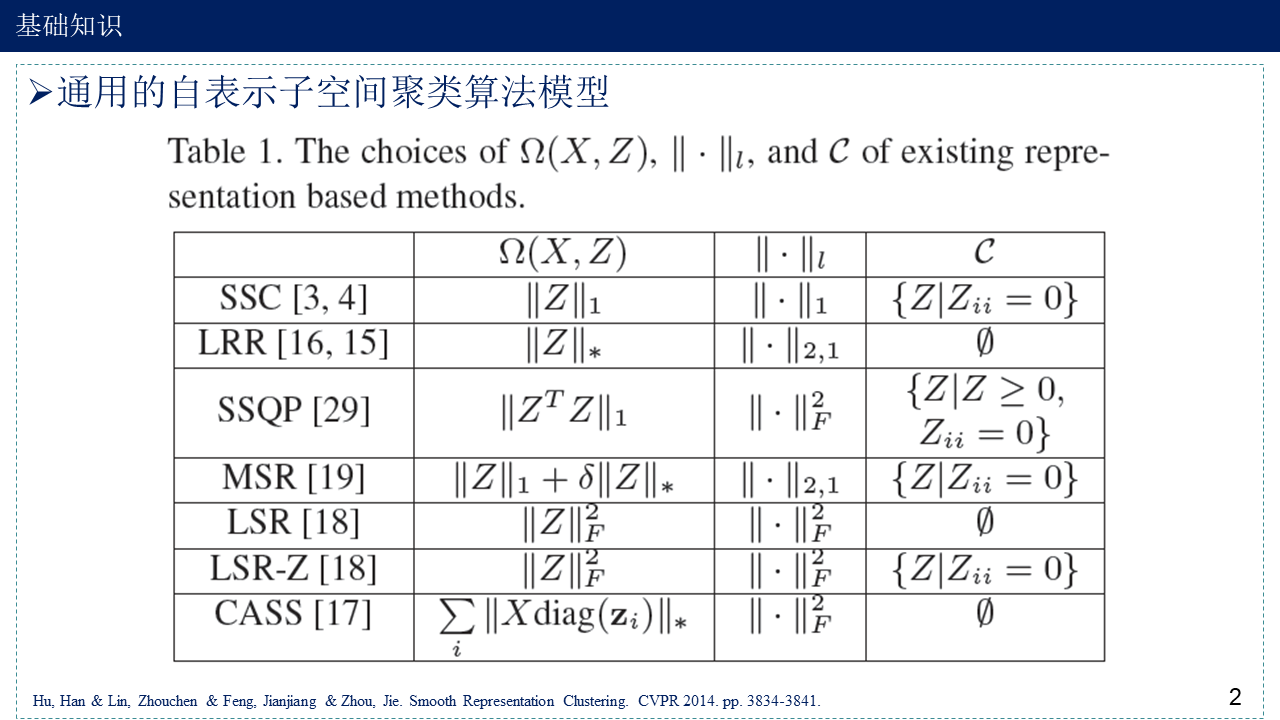
2. Low-Rank Tensor Constrained Multiview Subspace Clustering
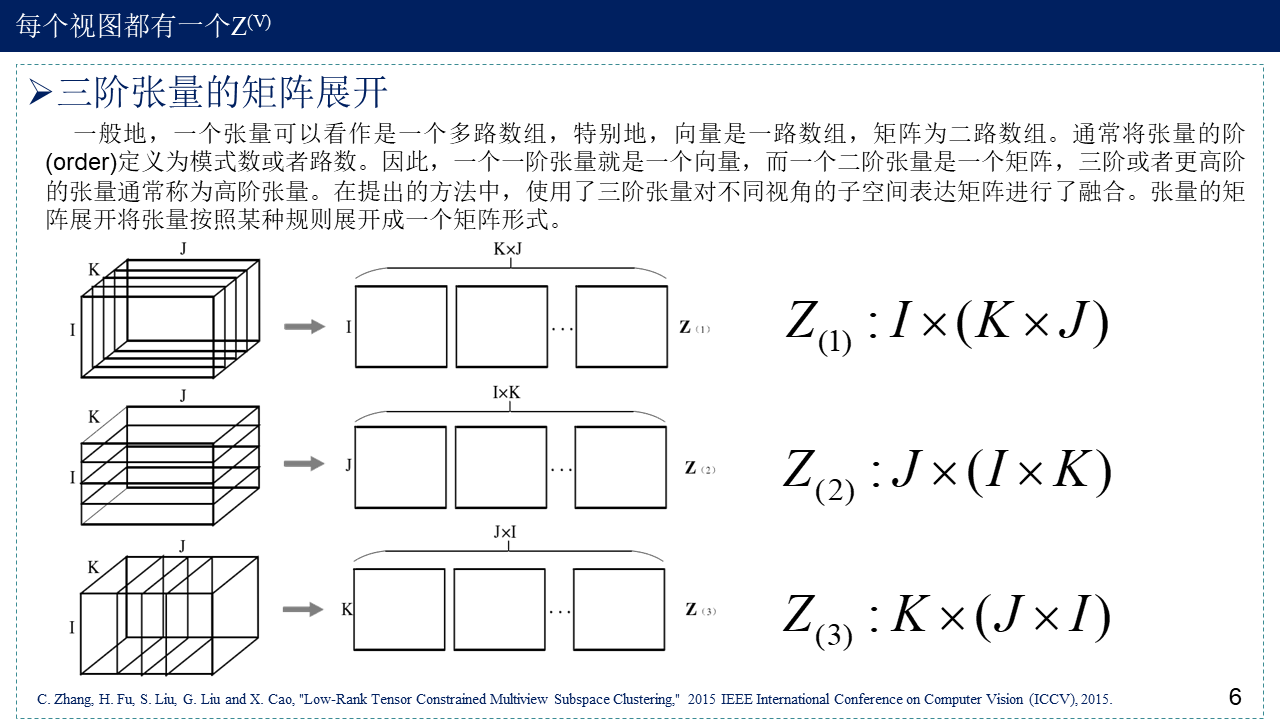
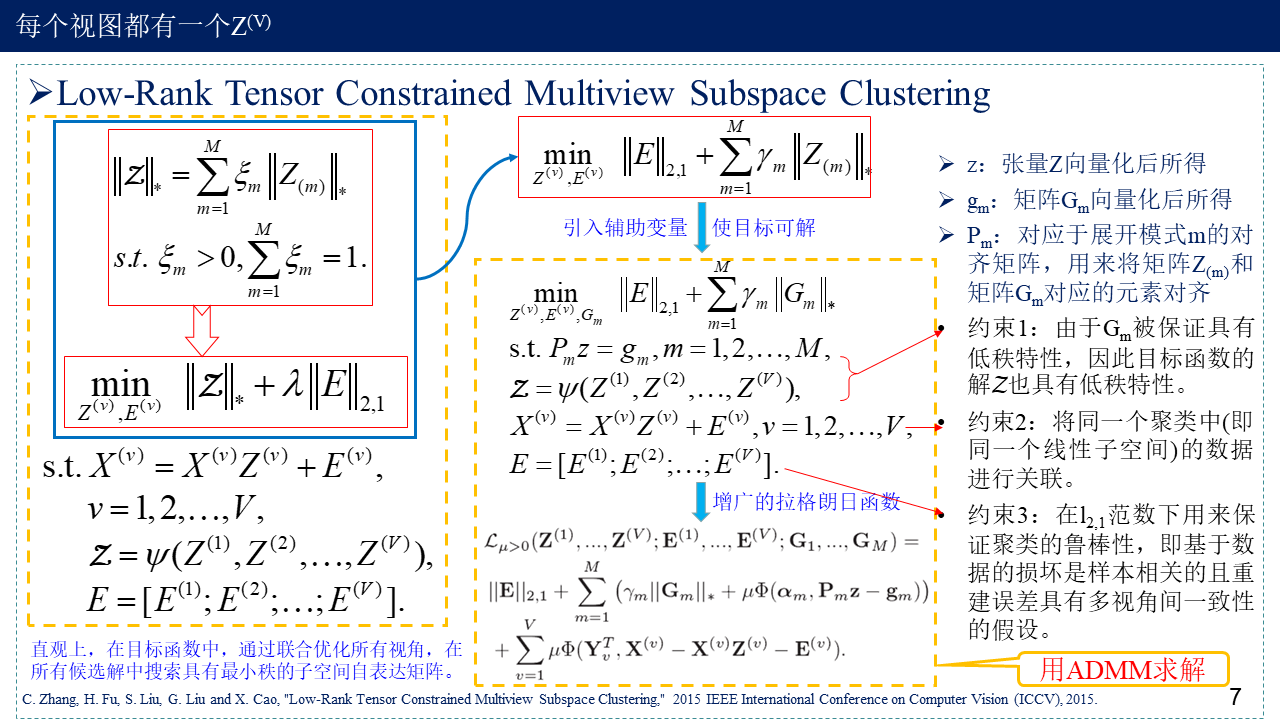
具体优化过程涉及到了矩阵的$L_{2,1}$范数与核范数的优化，E与G的优化详细见：一类涉及矩阵范数的优化问题。Z的优化中用到了置换/排列矩阵P的性质，置换矩阵是方阵，只取0和1两个值，且每行每列有且仅有一个1，置换矩阵也是正交矩阵，满足${P^T}P=P{P^T}=I$。
2015 ICCV论文代码可以在http://cic.tju.edu.cn/faculty/zhangchangqing/code.html中找到，关于代码里的公式优化理解问题可以参看2020 IJCV期刊文章3.4 Optimization这部分，代码里置换矩阵P并未体现，z和g向量化也并未用到，而是使用reshape()进行重塑矩阵大小，因此可以将两篇文章的优化过程结合一起看。值得注意的是$G_m$因三个不同模态导致矩阵大小不同，用奇异值阈值法计算完之后矩阵的大小分别为N*(N*V), N*(N*V), (N*N)*V，之后再用reshape()将每个模态下的矩阵重塑为N*N*V，即$g_m$由此产生。$g_m$一变，$\alpha _m$也跟着变，每个模态下的$\alpha _m$大小也是N*N*V。
3. Tensorized Multi-view Subspace Representation Learning
4. Generalized Latent Multi-View Subspace Clustering
这篇文章主要就是：X(数据，每个视图的)->H(潜在表示矩阵，公共的)->Z(系数矩阵，公共的)->W(构造相似度矩阵)->聚类。线性与非线性取决于X->H这里用的是线性映射，还是非线性映射(神经网络)。
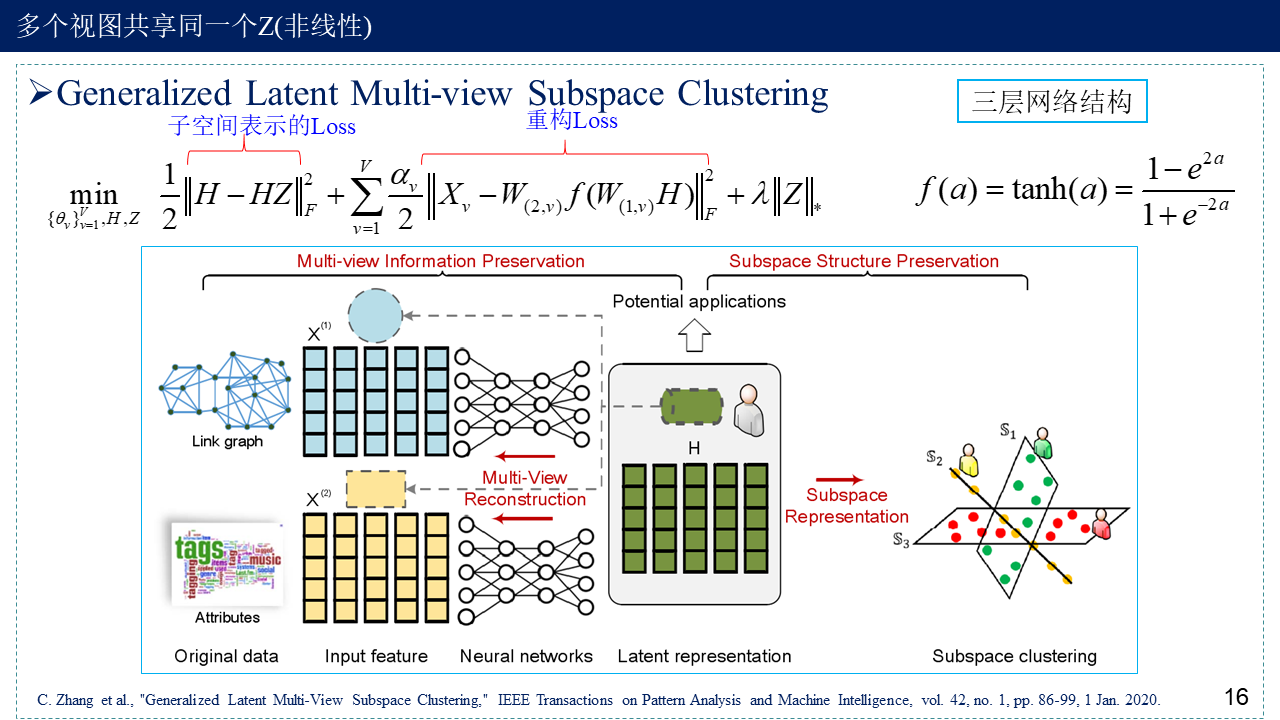
在更新Z的过程中，用到了ADMM方法，用辅助变量J代替原先核函数约束中的Z，原先是
$min \text{ } \frac{1}{2}\left \| H-HZ \right \|_{F}^{2}+\lambda \left \| Z \right \|_{*}$
现在增广拉格朗日函数为：
$min \text{ } \frac{1}{2}\left \| H-HZ \right \|_{F}^{2}+\lambda \left \| J \right \|_{*}+\frac{\mu }{2}\left \| J-Z \right \|_{F}^{2}+Y(J-Z)$
$Y=Y+\mu (J-Z)$
在求解J时，本应该是$L=\lambda \left \| J \right \|_{*}+\frac{\mu }{2}\left \| J-Z \right \|_{F}^{2}+Y(J-Z)$，L对J求偏导，但是，现在在L的基础上多加了一项${(\frac{Y}{\mu } )}^{2}$，因为本身L是最小化的，加一项非负项不影响最小化这个目标，这样就能凑一个平方项，就可以用已有的奇异值阈值收缩公式进行求解了。
5. Consistent and Specific Multi-View Subspace Clustering
6. 参考文献
[1] C. Zhang et al., "Low-Rank Tensor Constrained Multiview Subspace Clustering," 2015 IEEE International Conference on Computer Vision (ICCV), 2015.
Code: http://cic.tju.edu.cn/faculty/zhangchangqing/code.html
[2] 张长青. 基于自表达的多视角子空间聚类方法研究[D].天津大学,2016.
[3] C. Zhang et al., "Tensorized Multi-view Subspace Representation Learning," International Journal of Computer Vision 9(2020).
[4] C. Zhang et al., "Generalized Latent Multi-View Subspace Clustering," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 1, pp. 86-99, 1 Jan. 2020.
[5] C. Zhang et al., "Latent Multi-view Subspace Clustering," 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017.
[6] 张长青个人主页-天津大学智能与计算学部 http://cic.tju.edu.cn/faculty/zhangchangqing/research.html
[7] 交替方向乘子法（Alternating Direction Method of Multipliers）-凯鲁嘎吉 博客园
[8] Shirui Luo, Changqing Zhang, Wei Zhang, Xiaochun Cao, "Consistent and Specific Multi-View Subspace Clustering," AAAI. 2018.
Code: https://github.com/XIAOCHUN-CAS/Consistent-and-Specific-Multi-View-Subspace-Clustering/
[9] 有关多视图的会议论文：https://github.com/lslrh/multi-view
有关多视图论文的代码：https://github.com/liangnaiyao/multiview_learning
