第七章学习小结
查找
顺序表查找
概念
顺序表查找(Sequential Search)又叫线性查找,是最基本的查找技术。它的查找过程是:
-
从表中第一个(或最后一个)记录开始,逐个比较记录的关键字和给定值。
-
若某个记录的关键字和给定值相等,则查找成功。
-
若一直查找到最后一个(或第一个)记录,其关键字都不等于给定值,则查找失败。
int Sequential_search(int *a, int n, int key)
{
int i;
for(i = 1; i < n; i++){
if(a[i] == key){
return i;
}
}
return 0;
}
优化
int Sequential_search(int *a, int n, int key)
{
int i;
a[0] = key;
i = 1;
while(a[i] != key){
i--;
}
return i; // 当i等于0时查找失败
}
时间复杂度 :O(n)
折半查找
int Binary_search(int *a, int n, int key)
{
int low, high, mid;
low = 1;
high = n;
while(low <= high){
/*1*/ mid = (low + high) / 2;
if(key > a[mid]){
low = mid + 1;
}else if(key < a[mid]){
high = mid - 1;
}else{
return mid;
}
}
/*2*/ return 0;
}
分块查找
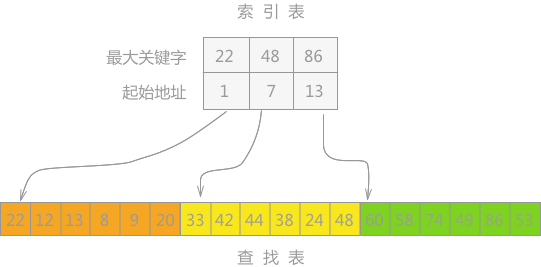
#include <stdio.h>
#include <stdlib.h>
struct index { //定义块的结构
int key;
int start;
} newIndex[3]; //定义结构体数组
int search(int key, int a[]);
int cmp(const void *a,const void* b){
return (*(struct index*)a).key>(*(struct index*)b).key?1:-1;
}
int main(){
int i, j=-1, k, key;
int a[] = {33,42,44,38,24,48, 22,12,13,8,9,20, 60,58,74,49,86,53};
//确认模块的起始值和最大值
for (i=0; i<3; i++) {
newIndex[i].start = j+1; //确定每个块范围的起始值
j += 6;
for (int k=newIndex[i].start; k<=j; k++) {
if (newIndex[i].key<a[k]) {
newIndex[i].key=a[k];
}
}
}
//对结构体按照 key 值进行排序
qsort(newIndex,3, sizeof(newIndex[0]), cmp);
//输入要查询的数,并调用函数进行查找
printf("请输入您想要查找的数:\n");
scanf("%d", &key);
k = search(key, a);
//输出查找的结果
if (k>0) {
printf("查找成功!您要找的数在数组中的位置是:%d\n",k+1);
}else{
printf("查找失败!您要找的数不在数组中。\n");
}
return 0;
}
int search(int key, int a[]){
int i, startValue;
i = 0;
while (i<3 && key>newIndex[i].key) { //确定在哪个块中,遍历每个块,确定key在哪个块中
i++;
}
if (i>=3) { //大于分得的块数,则返回0
return -1;
}
startValue = newIndex[i].start; //startValue等于块范围的起始值
while (startValue <= startValue+5 && a[startValue]!=key)
{
startValue++;
}
if (startValue>startValue+5) { //如果大于块范围的结束值,则说明没有要查找的数
return -1;
}
return startValue;
}
二叉排序树查找
要在二叉树中找出查找最大最小元素是极简单的事情,从根节点一直往左走,直到无路可走就可得到最小值;从根节点一直往右走,直到无路可走,就可以得到最大值。
查找最小关键字:
BST_P SearchMin(BST_P root)
{
if (root == NULL)
return NULL;
if (root->lchild == NULL)
return root;
else //一直往左孩子找,直到没有左孩子的结点
return SearchMin(root->lchild);
}
查找最大关键字:
BST_P SearchMax(BST_P root)
{
if (root == NULL)
return NULL;
if (root->rchild == NULL)
return root;
else //一直往右孩子找,直到没有右孩子的结点
return SearchMax(root->rchild);
}
二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2)若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3)任意节点的左、右子树也分别为二叉查找树。
二叉查找树性质:对二叉查找树进行中序遍历,即可得到有序的数列。
B树定义:
B树可以看作是对2-3查找树的一种扩展,即他允许每个节点有M-1个子节点。
-
根节点至少有两个子节点
-
每个节点有M-1个key,并且以升序排列
-
位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间
-
其它节点至少有M/2个子节点
B+树定义:
B+树是对B树的一种变形树,它与B树的差异在于:
- 有k个子结点的结点必然有k个关键码;
- 非叶结点仅具有索引作用,跟记录有关的信息均存放在叶结点中。
- 树的所有叶结点构成一个有序链表,可以按照关键码排序的次序遍历全部记录。
B和B+树的区别在于,B+树的非叶子结点只包含导航信息,不包含实际的值,所有的叶子结点和相连的节点使用链表相连,便于区间查找和遍历。
目标:
好好巩固已学知识,备战期末考。
参考资料:https://blog.csdn.net/sayhello_world/article/details/77200009


 浙公网安备 33010602011771号
浙公网安备 33010602011771号