《PDPU: An Open-Source Posit Dot-Product Unit for Deep Learning Applications》(一)
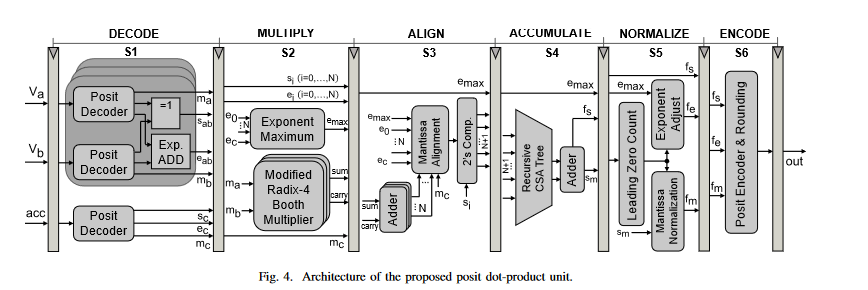
该架构图描述了一个基于Posit格式的定点-浮点混合运算单元(Dot-Product Unit, DPU),专注于高效实现乘积累加(MAC)操作。以下是分阶段解析:
1. 整体架构目标
- 功能:支持Posit格式的向量点乘(Dot-Product)运算,可能用于AI推理、信号处理等场景。
- 关键优化:通过多级流水线设计(图中隐含6级)和专用硬件加速乘法与对齐操作。
2. 各阶段详细分析
(1) DECODE阶段
- 功能:解码Posit操作数,提取符号、指数、尾数等字段。
- 组件:
- Postt Decoder:将Posit编码转换为内部处理格式(类似浮点的符号-指数-尾数拆分)。
- Exp. ADD:指数部分的预加法(为后续乘法对齐做准备)。
- Modified Radix-4 Booth Multiplier(重复两次):改进的基4 Booth乘法器,用于高效生成部分积(减少乘法步骤,提升速度)。
(2) MULTIPLY阶段(S1-S4)
-
S1-S2:部分积生成与初步压缩
- S1/S2:通过Booth算法生成部分积((S_1, S_2, \ldots)),并初步压缩(可能使用4:2压缩器)。
- Modified Radix-4 Booth:相比传统Booth算法,基4每步处理3位,减少部分积数量50%。
-
S3:无意义对齐(Meanless Alignment)
- 作用:可能是对部分积的位扩展或符号扩展(图中标注“无意义”可能为笔误,实际应为“符号扩展”或“位对齐”)。
-
S4:CSA树(Carry-Save Adder Tree)
- 功能:将部分积通过多层CSA树压缩为两个数(和与进位),为最终加法做准备。
(3) NORMALIZE阶段
- 功能:对乘法结果进行规范化,调整指数和尾数以满足Posit格式要求(类似浮点规格化)。
- 操作:检测前导零、移位尾数、调整指数。
(4) ENCODE阶段
- 功能:将结果重新编码为Posit格式,并进行舍入(Rounding)。
- 组件:
- Encoder & Rounding:处理尾数舍入(如四舍五入到最近偶数)、溢出检查等。
3. 关键优化技术
- Booth乘法器改进:Radix-4 Booth减少部分积数量,降低CSA树的复杂度。
- CSA树压缩:通过并行加法器树快速压缩部分积,缩短关键路径。
- Posit专用处理:针对Posit格式的动态范围特性(如可变指数位)优化解码/编码逻辑。
4. 潜在问题与改进
- 标注问题:
- “Meanless Alignment”应为“Meaningful Alignment”或具体说明(如“Sign Extension”)。
- S1-S2的(S_1, S_2, \ldots)未明确用途,可能是部分积的中间状态标识。
- 精度权衡:Posit的动态范围可能需要在归一化阶段增加额外逻辑。
5. 性能优势
- 高吞吐量:流水化设计允许每个时钟周期启动新操作。
- 能效比:Booth算法和CSA树减少了活跃硬件单元数量,降低功耗。
总结
该架构通过专用解码、高效乘法压缩树、Posit格式优化,实现了高精度点积运算的硬件加速,适合需要低功耗、高吞吐量的应用场景。需进一步验证对齐阶段的实现细节是否与设计目标一致。
与IEEE 754点积运算的对比分析
该架构与传统的基于IEEE 754浮点的点积运算单元(DPU)相比,不仅仅是增加了Posit的解码/编码模块,还在数据表示、运算逻辑、硬件优化等方面存在关键差异。以下是详细对比:
1. 数据格式差异
| 特性 | IEEE 754浮点 | Posit格式 |
|---|---|---|
| 结构 | 固定指数位宽(8/11位)+尾数 | 动态指数位宽(由regime控制) |
| 精度动态范围 | 固定(如FP32、FP16) | 更高动态范围(相同位数下优于浮点) |
| 特殊值处理 | NaN、±Inf、非规格化数 | 无NaN/Inf,但支持±0和±∞ |
| 舍入模式 | 多种(最近偶数、截断等) | 类似,但编码方式不同 |
影响:
- 解码/编码更复杂:Posit需要动态解析
regime和exp字段,而IEEE 754是固定结构。 - 硬件开销:Posit解码器需要额外的移位和逻辑运算,但可能减少乘法对齐的复杂度(因动态范围更优)。
2. 运算流程差异
(1)IEEE 754点积运算流程
- 解码:固定拆分符号、指数、尾数。
- 指数对齐:调整两数指数至相同(尾数移位)。
- 尾数乘法:用Booth或Wallace树计算乘积。
- 规格化:固定指数调整(如FP32的127偏置)。
- 舍入与编码:按标准舍入模式输出。
(2)Posit点积运算流程(如图中架构)
- 动态解码:解析
regime和exp,计算实际指数值(需额外逻辑)。 - 指数预加(Exp. ADD):提前计算乘积的指数(类似浮点,但需适应动态位宽)。
- 改进Booth乘法:采用Radix-4 Booth减少部分积数量。
- 无意义对齐(?):可能是动态位宽下的尾数对齐(与IEEE 754的固定移位不同)。
- CSA树压缩:与IEEE 754类似,但输入可能因Posit格式调整。
- 动态规格化:根据
regime重新计算指数范围。 - 编码与舍入:按Posit规则打包数据。
关键差异:
- 指数处理:Posit的
regime机制需要更复杂的动态调整逻辑。 - 对齐阶段:IEEE 754是固定移位,Posit可能需要条件移位(图中“Meanless Alignment”可能是笔误)。
- 硬件优化:Posit利用动态范围优势,可能减少乘法器的位宽需求。
3. 硬件实现差异
| 模块 | IEEE 754实现 | Posit实现(图中架构) |
|---|---|---|
| 解码器 | 固定位宽拆分(符号+指数+尾数) | 动态解析regime和exp(更复杂) |
| 乘法器 | 标准Booth或Wallace树 | Modified Radix-4 Booth(部分积更少) |
| 对齐逻辑 | 固定指数差移位 | 可能依赖动态位宽调整(标注不明确) |
| 规格化 | 固定偏置调整 | 动态regime重计算 |
| 编码器 | 固定格式打包 | 动态regime编码+舍入 |
优势与代价:
- Posit优势:相同位数下更高精度/动态范围,适合AI/ML场景。
- IEEE 754优势:标准化支持,硬件生态成熟(如GPU/CPU内置FPU)。
4. 是否“仅增加解码/编码模块”?
不是。除了解码/编码差异外,Posit点积运算还需:
- 动态指数处理:
regime和exp的动态计算影响乘法对齐逻辑。 - 专用乘法优化:如Radix-4 Booth可能针对Posit尾数位宽调整。
- 规格化适配:动态范围导致规格化逻辑更复杂。
- 舍入逻辑调整:Posit的舍入规则与IEEE 754不同(如向最近偶数舍入的实现细节差异)。
5. 总结
- 相同点:均使用流水线、Booth乘法、CSA树等经典算术优化技术。
- 不同点:
- Posit引入动态位宽解码/编码,影响整个数据通路。
- 硬件逻辑更复杂,但可能通过动态范围优化减少计算开销。
- 图中“Meanless Alignment”等标注需确认是否为设计特性或笔误。
应用场景建议:
- IEEE 754:兼容性优先(如通用计算)。
- Posit:需要高动态范围/精度的专用领域(如AI推理、雷达信号处理)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号