矩阵
矩阵
矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合 [1] ，最早来自于方程组的系数及常数所构成的方阵。
\[A=
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{pmatrix}
\]
方阵
行数与列数都等于n的矩阵A。记作：A\(_n\)。
如：
\[A_3\ast_3(方阵)=
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{pmatrix}
\]
\[A_3\ast_4(非方阵)=
\begin{pmatrix}
1 & 2 & 3 & 4\\
4 & 5 & 6 & 7\\
7 & 8 & 9 & 8\\
\end{pmatrix}
\]
\[A_4\ast_3(非方阵)=
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
10 & 11 & 12 \\
\end{pmatrix}
\]
单位矩阵
- 它是个"方形"矩阵（相同数目的行和列），
- 在对角线是 1，在其他位置是 0。
- 符号是大写字母 I。
- 单位矩阵可以是 2×2、或 3×3、4×4 等等
- 单位矩阵乘以其他矩阵（两个矩阵可以相乘）都为这个矩阵
\[I=
\left[
\begin{matrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right]
\]
对称矩阵
- 元素以对角线为对称轴对应相等的矩阵。
- 对于任何方形矩阵X，XT（T表示转置矩阵）是对称矩阵。
- 对角矩阵都是对称矩阵。
\[\left\{
\begin{matrix}
a & b & c & d \\
b & g & h & i \\
c & h & m & n \\
d & i & n & s
\end{matrix}
\right\}
\]
对角矩阵
- 对角矩阵是一个主对角线之外的元素皆为0的方阵。对角线上的元素可以为0或其他值。
\[\left[
\begin{matrix}
b & 0 & 0 & 0\\
0 & h & 0 & 0 \\
0 & 0 & n & 0 \\
0 & 0 & 0 & t
\end{matrix}
\right]
\]
零矩阵
- 零矩阵即所有元素皆为0的矩阵。
\[\left[
\begin{matrix}
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{matrix}
\right]
\]
矩阵的共轭
- 共轭矩阵，阵中每一个第i行第j列的元素都与第j行第i列的元素的共轭相等。
- \((A)_{ij}=\overline{A_{ij}}\)
- 共轭是改变两个项中间的正负号，像这样
- \(\text{3}x\)+1 共轭为：\(\text{3}x\)-1
一个2×2复数矩阵的共轭如下所示 ：
\[A=
\left[
\begin{matrix}
3+i & 4 \\
2-2i & i \\
\end{matrix}
\right]
\]
\[共轭矩阵为
\overline{A}=\left[
\begin{matrix}
3-i & 4 \\
2+2i & -i \\
\end{matrix}
\right]
\]
逆矩阵
- 矩阵一定要是"方形" （行和列数目相同）才能有逆矩阵。
- 设A是n阶矩阵，如果存在是n阶矩阵B使得AB=BA=I(单位矩阵)成立，则称A是可逆矩阵或非奇异矩阵，B是A的逆矩阵。
- 若A是可逆矩阵，则矩阵A的逆矩阵唯一，记为\(A^{−1}\)
- 公式：
- \((A^{-1})^{-1}=A\)
- \((kA)^{-1}=\frac {1} {k}A^{-1}(k\neq0)\)
- \((AB)^{-1}=B^{-1}A^{-1}\)
- \((A^n)^{-1}=(A^{-1})^n\)
- \((A^{-1})^T=(A^T)^{-1}\)
- \(|A^{-1}|=\frac{1}{|A|}\)
矩阵的转置
- 矩阵转置使用“T”表示
- 所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转，即得到转置。
- 矩阵的转置满足以下运算律
- \((A^T)^T=A\)
- \((\gamma A)^T=\gamma A^T\)
- \((AB)^T=B^TA^T\)
\[\left[
\begin{matrix}
a & b & c\\
f & g & h \\
k & l & m \\
p & q & r
\end{matrix}
\right]^T=
\left[
\begin{matrix}
a & f & k & p \\
b & g & l & q \\
c & h & m & r \\
\end{matrix}
\right]
\]
行列式
- 矩阵的行列式是一个可以从方形矩阵（方阵）计算出来的特别的数。
- 矩阵是数的排列：
- 行列式告诉我们矩阵的一些特性，这些特性对解线性方程组很有用，也可以帮我们找逆矩阵，并且在微积分及其他领域都很有用。
- 行列式的符号是每边一条垂直线。（和绝对值的符号一模一样。）
- \(|A|或det(A)\)代表矩阵 \(A\)的行列式.
- 定理：
- 设A为一n×n矩阵，则\(det(A^T)=det(A)\)
- 设A为一n×n三角形矩阵。则A的行列式等于A的对角元素的乘积。
- A为n×n矩阵。
- 若A有一行或一列包含的元素全为零，则\(det(A)=0。\)
- 若A有两行或两列相等，则\(det(A)=0。\)
- 基本介绍：一个n×n的方阵A的行列式记为det(A)或者|A|，
- 一个2×2矩阵的行列式可表示如下：
把公式记住的窍门是想：十字乘法：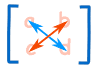
- 一个2×2矩阵的行列式可表示如下：
\[ det
\begin{pmatrix}
1 & 2 \\
3 & 4 \\
\end{pmatrix}=ad-bc
\]
- 3×3 矩阵的行列式可表示如下：
\(A= \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{pmatrix}\quad\quad\quad|A| = a(ei - fh) - b(di - fg) + c(dh - eg) \)
乍看很复杂，但这是有规律的：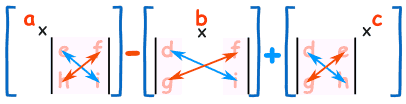
\[|A|=a*\begin{vmatrix}
e & f \\
h & i \\
\end{vmatrix}-b*\begin{vmatrix}
d & f \\
g & i \\
\end{vmatrix}+c*\begin{vmatrix}
d & e \\
g & h4 \\
\end{vmatrix}\]
求 3×3 矩阵的行列式：
+ 把 a 乘以不在 a 的行或列上的 2×2 矩阵的行列式。
+ 以 b 和 c 也做相同的计算
+ 把结果加在一起，不过 b 前面有个负号！
-
4×4 和更大的矩阵:
同一规律也适用于 4×4 矩阵：- 加：a 乘以 不在 a 的行或列 的矩阵 的行列式，
- 减：b 乘以 不在 b 的行或列 的矩阵 的行列式，
- 加：c 乘以 不在 c 的行或列 的矩阵 的行列式，
- 减：d 乘以 不在 d 的行或列 的矩阵 的行列式，
公式是：
\[|A|=a*
\begin{vmatrix}
f & g & h \\
j & k & l \\
n & o & p
\end{vmatrix}-b*\begin{vmatrix}
e & g & h \\
i & k & l \\
m & o & p
\end{vmatrix}+c*\begin{vmatrix}
e & f & h \\
i & j & l \\
m & n & p
\end{vmatrix}-d*\begin{vmatrix}
e & f & gh \\
i & j & k \\
m & n & 0
\end{vmatrix}
\]
留意 + - + - 的规律（+a 。。。-b 。。。+c 。。。-d 。。。）。 这很重要，要牢记。
- 运算规律
- \(|A^T|=|A|\)
- \(|\gamma A|=\gamma ^n|A|\)
- |AB|=|A||B|
- 虽然\(AB\neq BA,但是|AB|=|BA|\)
代数余子式
如矩阵：
\(A=
\begin{pmatrix}
3 & 0 & 2 \\
2 & 0 & -2 \\
0 & 1 & 1
\end{pmatrix}
\)
计算余子式:
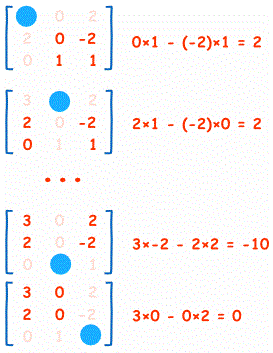
\(A_{11}的余子式为M_{11}:0*1-(-2)*1=2\)
\(A_{12}的余子式为M_{12}:2*1-(-2)*0=2\)
\(....\)
A的余子式矩阵为:
\[\begin{pmatrix}
0*1-(-2)*1 & 2*1-(-2)*0 & 2*1-0*0 \\
0*1-2*1 & 3*1-2*0 & 3*1-0*0 \\
0*(-2)-2*0 & 3*(-2)-2*2 & 3*0-0*2 \\
\end{pmatrix}=\begin{pmatrix}
2 & 2 & 2 \\
-2 & 3 & 3 \\
0 & -10 & 0 \\
\end{pmatrix}
\]
A的代数余子式矩阵为:
\[\begin{pmatrix}
2 & -2 & 2 \\
2 & 3 & -3 \\
0 & 10 & 0 \\
\end{pmatrix}
\]
\[A_{11}的代数余子式为(-1)^{1+1}*M_{11}=2
\]
\(A_{12}的代数余子式为(-1)^{1+2}*M_{12}=-2\)
\(....\)
伴随矩阵
伴随矩阵使用\(A^*\)表示
\(A^*=(A的代数余子式矩阵)^T\)
矩阵加减法
两个矩阵相加减：把对称位置的数相加减：
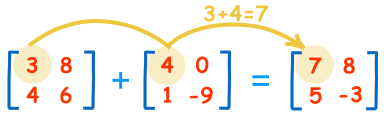
矩阵乘法
-
乘以常数
-
矩阵与矩阵相乘
(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58
(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64- 我们得到：
旋转矩阵
旋转矩阵(Rotation matrix)是在乘以一个向量的时候改变向量的方向但不改变大小的效果的矩阵。
- 二维旋转
- 2x2的方式
\[\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{bmatrix}
\]
实例：
\[\vec{A}(x,y)旋转\theta 得到\vec{A'}(x',y')=\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{bmatrix}*\begin{bmatrix}
x \\
y \\
\end{bmatrix}
\]
- 3x3的方式
\[\begin{bmatrix}
\cos\theta & -\sin\theta & 0\\
\sin\theta & \cos\theta & 0\\
0 & 0 & 1
\end{bmatrix}
\]
实例：\(\vec{A}(x,y,w),w等于1，没有意义。旋转\theta 得到\vec{A'}(x',y',1)=\begin{bmatrix} \cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{bmatrix}*\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}\)$
- 绕任意点旋转，只需要把三个矩阵乘起来。(先移动再选择后移动还原)
\[M=\left[
\begin{matrix}
1 & 0 & tx \\
0 & 1 & ty \\
0 & 0 & 1
\end{matrix}
\right]*\left[
\begin{matrix}
\cos\theta & -\sin\theta & 0 \\
\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{matrix}
\right]*\left[
\begin{matrix}
1 & 0 & -tx \\
0 & 1 & -ty \\
0 & 0 & 1
\end{matrix}
\right]=\left[
\begin{matrix}
\cos\theta & -\sin\theta & (1- \cos\theta)tx+ty * \sin\theta \\
\sin\theta & \cos\theta & (1- \cos\theta)ty-tx * \sin\theta \\
0 & 0 & 1
\end{matrix}
\right]
\]
- 三维旋转
- 绕X轴的旋转\(\theta\),4x4矩阵的形式:
\[\left[
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta & -\sin\theta & 0 \\
0 & \sin\theta & \cos\theta & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right]
\]
实例：\(\vec{A}(x,y,z,1),w等于1，没有意义。绕X轴旋转\theta 得到\vec{A'}(x',y',z',1)=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]*\left[ \begin{matrix} x \\ y \\ z \\ 1 \end{matrix} \right]\)
- 绕Y轴的旋转\(\theta\),4x4矩阵的形式\( \left[ \begin{matrix} \cos\theta & 0 & -\sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ \sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \)
- 绕Z轴的旋转\(\theta\),4x4矩阵的形式\( \left[ \begin{matrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \)
- 绕任意轴(a,b,c)旋转\(\theta\),4x4矩阵的形式
平移矩阵
- 二维向量\(A(x,y)向x移动x',向y移动y'\)。平移矩阵为：\( \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ x' &y' & 1 \\ \end{matrix} \right] \)
- 三维向量\(A(x,y,z)向x移动x',向y移动y',向z移动y'\)。平移矩阵为：\( \left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ x' &y' & z' & 1 \end{matrix} \right] \)
缩放矩阵
- 二维向量\(A(x,y)向x缩放x',向y縮放y'\)。缩放矩阵为：\( \left[ \begin{matrix} x' & 0 & 0 \\ 0 & y' & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \)
- 三维向量\(A(x,y,z)向x缩放x',向y縮放y',向z缩放z'\)。缩放矩阵为：\( \left[ \begin{matrix} x'& 0 & 0 & 0 \\ 0 & y' & 0 & 0 \\ 0 & 0 & z' & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \)
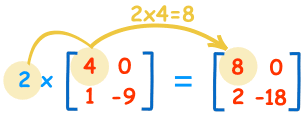
浙公网安备 33010602011771号