导数

导数（微分）

导数是函数的 "变率"，就是函数的坡度。
导数就是函数的变化率

导数入门

求函数 y = f(x) 的导数，我们用坡度的公式：

$$ 导数（坡度）（斜率） =F(x)'=\frac{\textx}{\texty}=\frac{Y 的改变}{X 的改变}=\frac{Δy}{Δx}$$

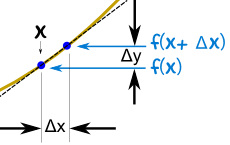
我们看到（如图）:

• $x 从 x 变到 x+Δx $
• \(y 从 f(x) 变到 f(x+Δx)\)

按照这步骤去做：

• $代入这个坡度公式：\frac{Δy}{Δx}=\frac{ f(x+Δx) − f(x)}{Δx} $
• \(尽量简化\)
• \(把 Δx 缩小到零。\)

像这样：

我们写 \(dx\)，而不写 "\(Δx\) 趋近 0"，所以 "的导数" 通常是写成$\frac{\textx}{\texty}$

• \(\frac{d}{dx}x^2=2x\)
• \(“x^2 的导数等于 2x"\)
• \(或 “x2 的 d \space dx 等于 2x"\)

\(\frac{d}{dx}x^2=2x 的意思是什么\)

\(意思是，对于函数 x^2，在任何一点的坡度或 "变化率" 是 2x。\)

再来看一个例子。

一些简单函数的简单导数如下：

• \(\frac{d}{dx}x^n=nx^{n-1}\)
• \(\frac{d}{dx}\ln{x}=\frac{1}{x}\)
• \(\frac{d}{dx}\sin{x}=\cos{x}\)
• \(\frac{d}{dx}\cos{x}=-\sin{x}\)
• \(\frac{d}{dx}\tan{x}=\frac{d}{dx}\frac{\sin{x}}{\cos{x}}=\frac{1}{(\cos{x})^2}=\sec^2{x}\)
• \(\frac{d}{dx}\csc{x}=-\csc{x}\cot{x}\)
• \(\frac{d}{dx}\sec{x}=\sec{x}\tan{x}\)
• \(\frac{d}{dx}\cot{x}=-\csc^2{x}\)
• \(\frac{d}{dx}e^x=e^x\)
• \(\frac{d}{dx}a^x=(\ln{a})a^x\)
• \(\frac{d}{dx}\sin{^{-1}}x=\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{dx}\cos{^{-1}}x=-\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{dx}\tan{^{-1}}x=\frac{1}{1+x^2}\)
• \(\frac{d}{dx}\cot{^{-1}}x=-\frac{1}{1+x^2}\)
• \(\frac{d}{dx}\sec{^{-1}}x=\frac{1}{x\sqrt{x^2-1}}\)
• \(\frac{d}{dx}\csc{^{-1}}x=-\frac{1}{x\sqrt{x^2-1}}\)
• \(\frac{d}{dx}\sinh{x}=\cosh{x}\)
• \(\frac{d}{dx}\cosh{x}=\sinh{x}\)
• \(\frac{d}{dx}\tanh{x}=sech^2{x}\)
• \(\frac{d}{dx}\coth{x}=- \text{csch}^2x\)
• \(\frac{d}{dx}\text{sech}\space x=-\text{sech}\space x\space\text{tanh}\space x\)
• \(\frac{d}{dx}\text{sech}\space x=-\text{csch}\space x \space\text{coth}\space x\)
• \(\frac{d}{dx}\text{sn}\space x=\text{cn}\space x\space\text{dn}\space x\)
• \(\frac{d}{dx}\text{cn}\space x=-\text{sn}\space x\space\text{dn}\space x\)
• \(\frac{d}{dx}\text{dn}\space x=-k^2\text{sn}\space x\space\text{cn}\space x\)

导函数的运算

求和的导数等于导数的总和：
\((f+...+h)'=f'+...+h'\)
如果C是常数:
\(\frac{d}{dx}[c\space f(x)]=cf'(x)\)
微分状态 的乘积规则:
\((f(x)g(x))'=f(x)g'(x)+f'(x)g(x)\)
三个或更多函数的乘积的导数规则:
$$[f\space g\space h]'=(f\space g)h'+(f\space g)'h=f\space g\space h'+(f\space g'+f'\space g)h=f'\space g\space h+f\space g'\space h+f\space g\space h' $$

导数 的商规则:
\(\frac{d}{dx}[\frac{f(x)}{g(x)}]=\frac{g(x)f'(x)-f(x)g'(x)}{(g(x))^2}\)

而幂律给出：
\(\frac{d}{dx}(x^n)=nx^{n-1}\)