
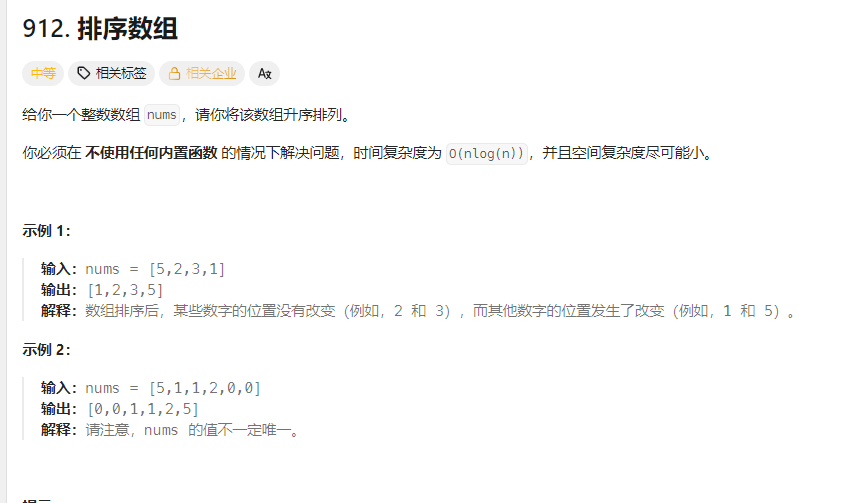
一、题目描述
二、算法原理
通过根据题目要求我们要把一个数组变成一个升序的数组,而且时间复杂度为:O(n log( n )) ,这里我们使用快排来解决这道题,不懂快排的能够看这篇博客:
通过不过我们要把快排进行一下修改,基准值的我们利用随机值:rand () ,根据算法导论可得:这个随机的标准值能够接近于:O(n logn )
而且我们不使用原来快排的比较数值大小的方式,我们使用分治的思想:
假设大家随机选择的基准值为1,那么一轮查找之后,数组里面所有的1都会呆在该待的数组的位置:
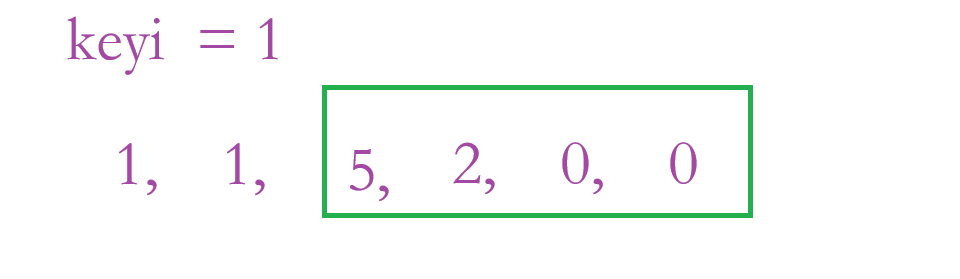
此时,我们就在绿色数组里面,再随机找一个随机值来作为基准值,再固定这个基准值的在数组的位置,最后不断的划分,直到这个数组变成有序。
三、代码实现
class Solution {
public:
vector sortArray(vector& nums) {
srand(time(NULL));
int n = nums.size();
Quicksort(0,n - 1,nums);
return nums;
}
void Quicksort(int l,int r,vector& nums)
{
if(l >= r) return;
int keyi = Get(l,r,nums);
int i = l;
int left = l - 1;
int right = r + 1;
while(i < right)
{
if(nums[i] > keyi) swap(nums[i],nums[--right]);
else if(nums[i] == keyi) i++;
else swap(nums[++left],nums[i++]);
}
Quicksort(l,left,nums);//zuobian
Quicksort(right,r,nums);//右边
}
int Get(int l,int r,vector& nums)
{
int tmp = rand();
return nums[ l + (tmp % (r - l + 1)) ];
}
}; 
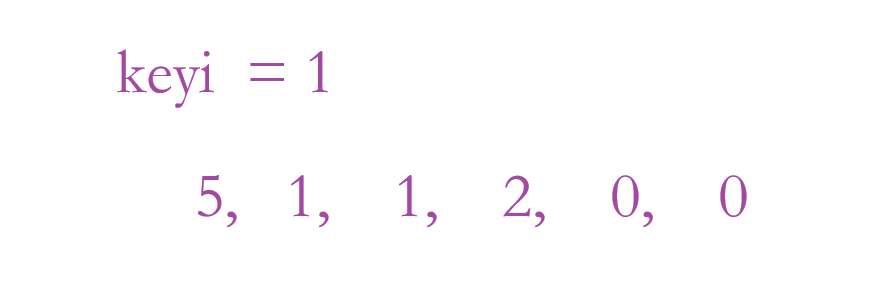


 浙公网安备 33010602011771号
浙公网安备 33010602011771号