
目录
一、路径类 DP 核心逻辑:用 “位置” 定义状态,用 “方向” 推导转移
例题 1:数字三角形(洛谷 P1216)—— 路径类 DP 入门题
例题 2:矩阵的最小路径和(牛客 DP11)—— 路径类 DP 的 “导航基础题”
例题 3:“木” 迷雾森林(牛客网)—— 路径类 DP 的 “障碍迷宫题”
例题 4:过河卒(洛谷 P1002)—— 路径类 DP 的 “障碍 + 特殊约束题”
前言
如果你玩过《推箱子》这类游戏,一定对 “规划路径” 不陌生 —— 从起点到终点,每一步都要考虑方向、障碍、收益,最终找到最优路线。而算法世界里的 “路径类线性 DP”,本质就是解决这类 “地图导航” 问题的利器。
作为线性 DP 的重要分支,路径类 DP 的核心特点是状态与 “位置” 强绑定—— 无论是二维矩阵的
(i,j)坐标,还是环形地图的特殊点位,状态定义都离不开 “当前走到哪了”,状态转移则围绕 “下一步能往哪走” 展开。相比于基础线性 DP(如最大子段和),路径类 DP 更贴近 “场景化问题”,比如求最小路径和、统计可行路径数、避开障碍找最优解等。但只要掌握 “位置定义状态,方向推导转移” 的核心逻辑,就能轻松拿下这类题。
今天这篇文章,就带大家从 “入门到精通” 吃透路径类线性 DP:从最经典的 “数字三角形” 入手,到矩阵最小路径和、迷雾森林迷宫、过河卒避马难题,每道题都拆解清楚 “状态设计→转移推导→代码实现→优化技巧”,最后再总结通用解题模板。哪怕你是刚接触 DP 的新手,跟着步骤走也能完全掌握!下面就让我们正式开始吧!
一、路径类 DP 核心逻辑:用 “位置” 定义状态,用 “方向” 推导转移
在正式讲例题前,我们先搞懂路径类 DP 的 “底层逻辑”—— 为什么它能解决地图路径问题?核心思路是什么?
1.1 路径类 DP 的本质:位置即状态,移动即转移
路径类 DP 的核心是把 “当前所在位置” 作为状态的核心要素,比如在二维矩阵中,用dp[i][j]表示 “走到第 i 行第 j 列时的某种目标值(如路径和、方案数)”。而状态转移的本质,就是 “从当前位置能到达的下一个位置,如何继承当前状态的信息”。
举个简单例子:如果只能向右或向下走,那么走到(i,j)的前一步,只能是(i-1,j)(从上方下来)或(i,j-1)(从左方过来)。这种 “移动方向限制”,直接决定了状态转移方程的推导逻辑。
1.2 路径类 DP 解题四步曲(通用模板)
和所有线性 DP 一样,路径类 DP 也有固定的解题流程,记住这四步,90% 的题都能套用:
第一步:明确定义状态(最关键)
用dp[i][j]表示 “走到位置(i,j)时的目标值”,目标值根据题目需求确定:
- 求最小 / 最大路径和:
dp[i][j]= 走到(i,j)的最小 / 最大路径和;- 求可行路径数:
dp[i][j]= 走到(i,j)的不同路径总数;- 求特殊约束路径:
dp[i][j]= 走到(i,j)且满足某条件(如不经过障碍)的目标值。
第二步:推导状态转移方程(核心逻辑)
根据 “允许的移动方向” 和 “题目目标” 推导:
- 方向限制:比如只能向右 / 向下 / 向上 / 向左,或多方向结合;
- 目标限制:比如求最小和就取前序状态的最小值,求方案数就累加前序状态的方案数;
- 特殊约束:比如遇到障碍时
dp[i][j] = 0(不可达),遇到特殊点时跳过。
第三步:初始化(避免逻辑漏洞)
路径类 DP 的初始化通常围绕 “起点” 和 “边界”:
- 起点初始化:比如起点
(1,1)的dp[1][1]= 起点本身的值(路径和)或 1(方案数);- 边界初始化:比如第一行只能从左向右走,所以
dp[1][j] = dp[1][j-1] + a[1][j](路径和);第一列只能从上向下走,同理。
第四步:确定填表顺序(保证正确性)
填表顺序必须满足 “计算当前状态时,依赖的前序状态已计算完成”:
- 若只能向右 / 向下:从左到右、从上到下填表;
- 若只能向上 / 向右:从下到上、从左到右填表;
- 若有环形或多方向:需特殊处理(如倍增数组),但基础路径类 DP 很少涉及。
1.3 路径类 DP 的两大优化方向
路径类 DP 的优化主要集中在 “空间” 上,因为二维dp数组在矩阵规模较大时(如1e3×1e3)会占用较多内存,常见优化技巧有:
- 滚动数组优化:若
dp[i][j]只依赖上一行(i-1)或同一行的前半部分(j-1),可用一维数组替代二维数组,空间复杂度从O(nm)降至O(m);- 边界压缩:将矩阵的无效区域(如障碍、越界位置)提前处理,减少不必要的计算。
二、经典例题实战:从基础到进阶,吃透路径类 DP
接下来我们通过 4 道经典例题,一步步套用 “解题四步曲”,从简单到复杂,彻底掌握路径类 DP 的逻辑。每道题都会详细拆解思路,附上完整代码和优化版本,确保你能看懂、会用、能举一反三。
例题 1:数字三角形(洛谷 P1216)—— 路径类 DP 入门题
题目描述:从金字塔顶端到低端的最大路径和
给定一个r行的数字三角形(金字塔形状),每次只能走到左下方或右下方的点,求从顶端走到低端任意位置的路径上,数字和的最大值。
输入:第一行是行数r(1≤r≤1000),后面r行是数字三角形的每一行(每个数字 0~100);
输出:最大路径和。
示例输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5示例输出:30(路径:7→3→8→7→5)
思路拆解(四步曲套用)
第一步:定义状态
数字三角形是二维结构,且路径方向固定(左下 / 右下),因此定义:dp[i][j] = 从顶端(1,1)走到第i行第j列时的最大路径和。
目标是求第r行所有dp[r][j]中的最大值(因为可以走到低端任意位置)。
第二步:推导状态转移方程
走到(i,j)的前一步只有两种可能:
- 从上方
(i-1,j)走下来(因为(i-1,j)的右下方是(i,j));- 从左上方
(i-1,j-1)走下来(因为(i-1,j-1)的右下方是(i,j))。
因此,dp[i][j] = 两种前序状态的最大值 + 当前位置的数字,即:dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + a[i][j]
这里a[i][j]表示第i行第j列的数字。
第三步:初始化
- 顶端初始化:
dp[1][1] = a[1][1](起点只有一个,路径和就是自身);- 边界处理:第
i行有i个数字,j的范围是1~i。对于j=1(每行第一个元素),只能从(i-1,1)走下来,所以dp[i][1] = dp[i-1][1] + a[i][1];对于j=i(每行最后一个元素),只能从(i-1,i-1)走下来,所以dp[i][i] = dp[i-1][i-1] + a[i][i]。
第四步:填表顺序
从第 2 行开始,每行从左到右填表(因为dp[i][j]依赖dp[i-1][j]和dp[i-1][j-1],上一行已计算完成)。
代码实现(基础版:二维数组)
#include
#include
using namespace std;
const int N = 1010; // 因为r最大1000,数组开1010足够
int r;
int a[N][N]; // 存储数字三角形
int dp[N][N]; // dp[i][j]:走到(i,j)的最大路径和
int main() {
cin >> r;
// 读取数字三角形(注意:第i行有i个元素)
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= i; j++) {
cin >> a[i][j];
}
}
// 初始化:顶端
dp[1][1] = a[1][1];
// 填表:从第2行到第r行
for (int i = 2; i <= r; i++) {
// 处理每行第一个元素(j=1)
dp[i][1] = dp[i-1][1] + a[i][1];
// 处理每行中间元素(2<=j<=i-1)
for (int j = 2; j < i; j++) {
dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + a[i][j];
}
// 处理每行最后一个元素(j=i)
dp[i][i] = dp[i-1][i-1] + a[i][i];
}
// 找第r行的最大值
int max_sum = 0;
for (int j = 1; j <= r; j++) {
max_sum = max(max_sum, dp[r][j]);
}
cout << max_sum << endl;
return 0;
} 优化:滚动数组(空间从 O (r²)→O (r))
观察状态转移方程:dp[i][j]只依赖上一行(i-1)的j和j-1位置,不需要存储所有行的dp值。因此可以用一维数组dp[j]替代二维数组,通过 “从右向左” 填表避免覆盖前序状态。
优化后代码:
#include
#include
using namespace std;
const int N = 1010;
int r;
int a[N][N];
int dp[N]; // 一维数组:dp[j]表示当前行第j列的最大路径和
int main() {
cin >> r;
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= i; j++) {
cin >> a[i][j];
}
}
// 初始化:第一行
dp[1] = a[1][1];
// 填表:从第2行开始,每行从右向左填
for (int i = 2; i <= r; i++) {
// 从右向左:避免dp[j-1]被覆盖(如果从左向右,dp[j]会覆盖dp[j-1],影响后续计算)
for (int j = i; j >= 1; j--) {
if (j == 1) {
// 每行第一个元素:只能从上方下来
dp[j] = dp[j] + a[i][j];
} else if (j == i) {
// 每行最后一个元素:只能从左上方下来
dp[j] = dp[j-1] + a[i][j];
} else {
// 中间元素:取上一行j和j-1的最大值
dp[j] = max(dp[j], dp[j-1]) + a[i][j];
}
}
}
// 找最大值
int max_sum = 0;
for (int j = 1; j <= r; j++) {
max_sum = max(max_sum, dp[j]);
}
cout << max_sum << endl;
return 0;
} 优化解析
为什么要 “从右向左” 填表?因为一维数组dp[j]存储的是上一行的状态:
- 如果从左向右填,计算
dp[j]时会覆盖dp[j-1],而后续计算dp[j+1]需要上一行的dp[j](已被覆盖),导致错误;- 从右向左填时,
dp[j]依赖的dp[j](上一行的j)和dp[j-1](上一行的j-1)都还没被覆盖,计算正确。
这种优化在矩阵规模较大时(如1e3×1e3)效果明显,能节省大量内存。
例题 2:矩阵的最小路径和(牛客 DP11)—— 路径类 DP 的 “导航基础题”
题目链接:https://www.nowcoder.com/practice/38ae72379d42471db1c537914b06d48e?tpId=230&tqId=39755&ru=/exam/o
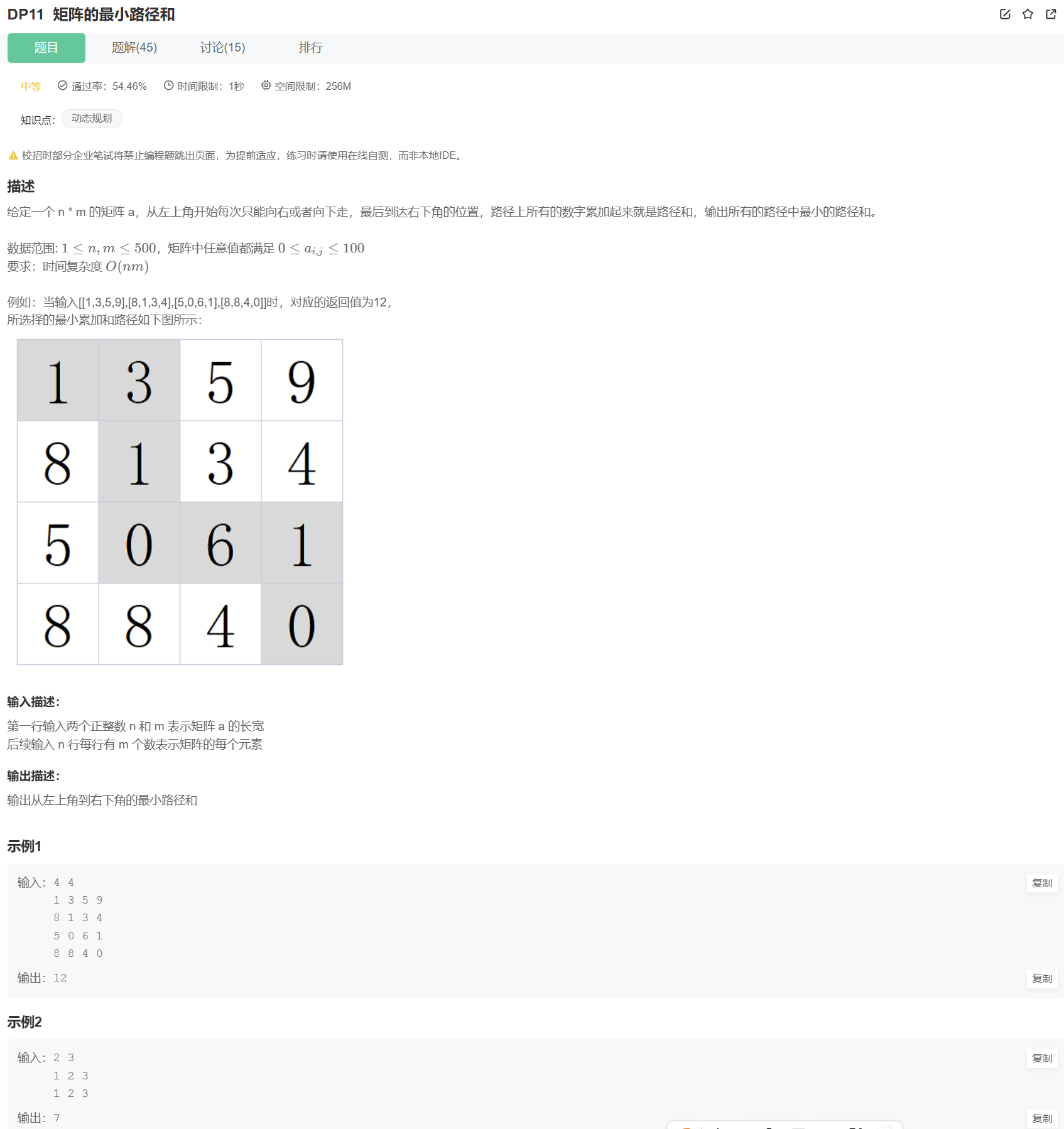
题目描述:从左上角到右下角的最小代价
给定一个n×m的矩阵,每次只能向右或向下走,求从左上角(1,1)到右下角(n,m)的路径上,所有数字的和的最小值。
输入:第一行是n和m(1≤n,m≤500),后面n行是矩阵元素(0≤a [i][j]≤100);
输出:最小路径和。
示例输入:
4 4
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0示例输出:12(路径:1→3→1→0→6→1→0)
思路拆解(四步曲套用)
第一步:定义状态
矩阵路径问题,目标是 “最小路径和”,因此定义:dp[i][j] = 从(1,1)走到(i,j)的最小路径和。
目标是dp[n][m](因为必须走到右下角)。
第二步:推导状态转移方程
只能向右或向下走,所以走到(i,j)的前一步只有两种可能:
- 从上方
(i-1,j)向下走:路径和 =dp[i-1][j] + a[i][j];- 从左方
(i,j-1)向右走:路径和 =dp[i][j-1] + a[i][j]。
要找最小值,因此转移方程:dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + a[i][j]
第三步:初始化
需要处理第一行和第一列(边界):
- 第一行:只能从左向右走,所以
dp[1][j] = dp[1][j-1] + a[1][j](比如dp[1][2] = dp[1][1] + a[1][2],dp[1][3] = dp[1][2] + a[1][3]);- 第一列:只能从上向下走,所以
dp[i][1] = dp[i-1][1] + a[i][1];- 起点:
dp[1][1] = a[1][1](初始状态)。
但这里有个小技巧:为了避免边界判断(比如i=1或j=1时的特殊处理),可以将dp数组的规模扩大一行一列(dp[0..n][0..m]),并将dp[0][1]或dp[1][0]初始化为 0,其他无效位置初始化为无穷大(0x3f3f3f3f),这样可以统一转移方程。
第四步:填表顺序
从左到右、从上到下(因为dp[i][j]依赖dp[i-1][j](上一行已算完)和dp[i][j-1](同一行左边已算完))。
代码实现(基础版:二维数组 + 边界优化)
#include
#include // 用于memset
#include
using namespace std;
const int N = 510; // n和m最大500,开510足够
int n, m;
int a[N][N]; // 存储矩阵
int dp[N][N]; // dp[i][j]:走到(i,j)的最小路径和
int main() {
cin >> n >> m;
// 读取矩阵
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
}
}
// 初始化:将dp数组填充为无穷大,避免无效状态干扰
memset(dp, 0x3f, sizeof(dp));
// 起点的前序状态:dp[0][1] = 0(或dp[1][0] = 0),保证dp[1][1]计算正确
dp[0][1] = 0;
// 填表:从左到右,从上到下
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 统一转移方程:不需要判断边界(因为dp[0][j]和dp[i][0]都是无穷大,不影响min结果)
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + a[i][j];
}
}
// 输出右下角的最小路径和
cout << dp[n][m] << endl;
return 0;
} 代码解析:为什么用 “无穷大” 初始化?
- 无效状态(如
dp[0][j]、dp[i][0])表示 “无法到达的位置”,它们的路径和应该是无穷大;- 当计算第一行
dp[1][j]时,dp[i-1][j] = dp[0][j] = 无穷大,所以min(无穷大, dp[1][j-1])会自动取dp[1][j-1],符合 “第一行只能从左向右” 的逻辑;- 同理,第一列
dp[i][1]会自动取dp[i-1][1],符合 “第一列只能从上向下” 的逻辑;- 这种方式避免了单独写
if (i==1)或if (j==1)的判断,代码更简洁。
优化:滚动数组(空间 O (nm)→O (m))
观察转移方程:dp[i][j]只依赖上一行的dp[i-1][j]和同一行的dp[i][j-1],因此可用一维数组dp[j]存储,每次更新时覆盖上一行的状态。
优化后代码:
#include
#include
#include
using namespace std;
const int N = 510;
int n, m;
int a[N][N];
int dp[N]; // 一维数组:dp[j]表示当前行第j列的最小路径和
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
}
}
// 初始化:无穷大
memset(dp, 0x3f, sizeof(dp));
// 起点的前序状态:dp[0] = 0(因为第一行第一个元素dp[1] = min(dp[0], dp[0]) + a[1][1] = 0 + a[1][1])
dp[0] = 0;
// 填表:逐行处理,每行从左到右
for (int i = 1; i <= n; i++) {
// 处理当前行的第一个元素(j=1):只能从上一行的j=1下来
dp[1] = dp[1] + a[i][1];
// 处理当前行的其他元素(j>=2)
for (int j = 2; j <= m; j++) {
// dp[j](上一行的j)和dp[j-1](当前行的j-1)取min,加上当前元素
dp[j] = min(dp[j], dp[j-1]) + a[i][j];
}
}
cout << dp[m] << endl;
return 0;
} 优化解析
- 逐行处理时,
dp[j]初始存储的是上一行的dp[j](即dp[i-1][j]);- 处理当前行
j=1时,只能从上一行j=1下来,所以dp[1] = dp[1](上一行) + a[i][1];- 处理
j>=2时,dp[j]= min (上一行的dp[j](未被覆盖), 当前行的dp[j-1](已计算)) + a [i][j],逻辑正确;- 空间从
O(nm)降至O(m),对于n=1e3、m=1e3的矩阵,内存占用从 1e6 降到 1e3,效果显著。
例题 3:“木” 迷雾森林(牛客网)—— 路径类 DP 的 “障碍迷宫题”
题目链接:https://ac.nowcoder.com/acm/problem/53675
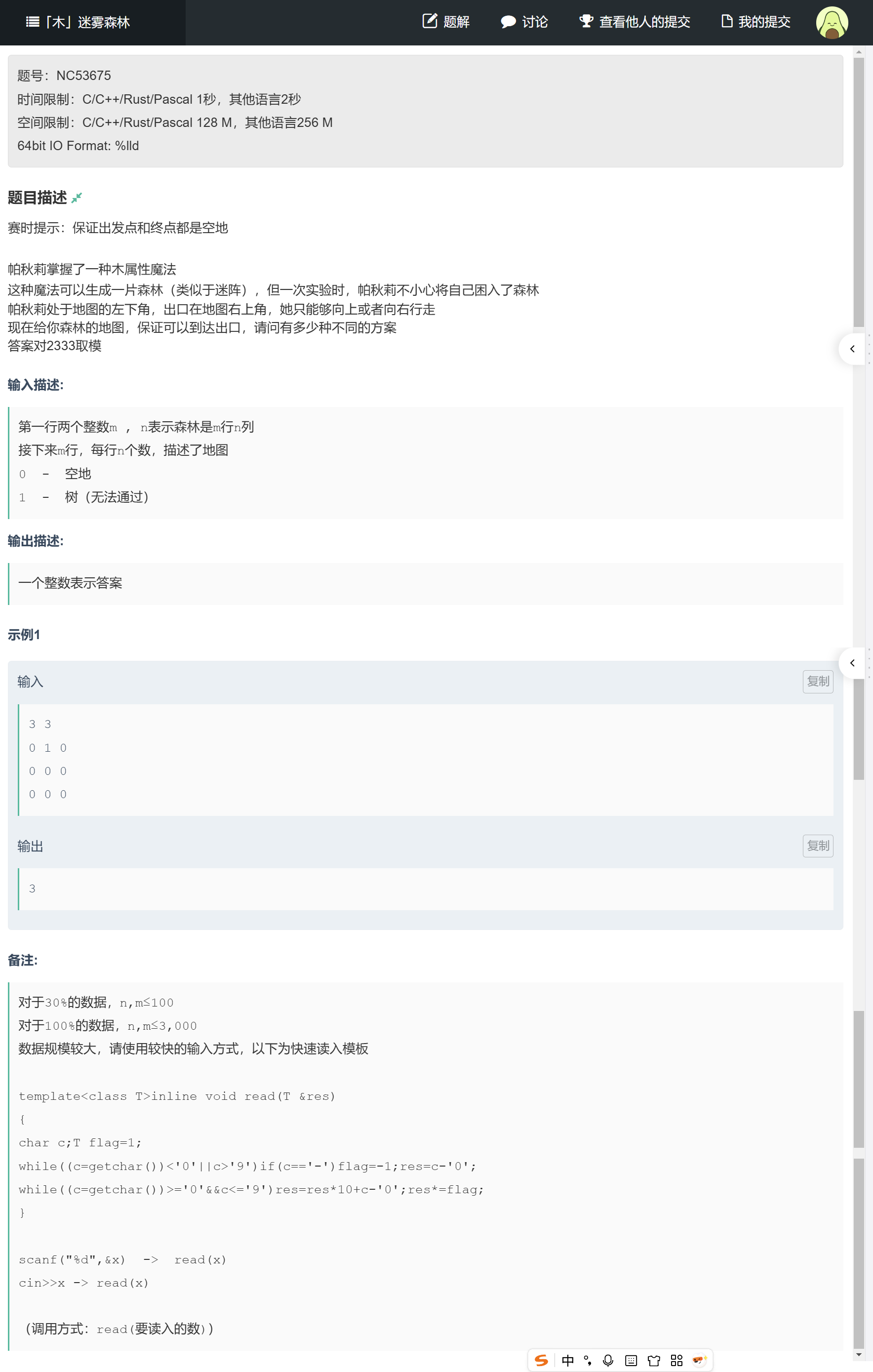
题目描述:从左下角到右上角的路径计数
帕秋莉被困在m行n列的森林迷宫里,起点在左下角(m,1),出口在右上角(1,n),每次只能向上或向右走。迷宫中有 “树”(标记为 1),无法通过;“空地”(标记为 0)可通过。求从起点到出口的不同路径数,结果对 2333 取模。
输入:第一行是m和n(1≤m,n≤3000),后面m行是迷宫矩阵(0 或 1);
输出:路径数(对 2333 取模)。
示例输入:
3 3
0 1 0
0 0 0
0 0 0示例输出:3(路径:(3,1)→(3,2)→(3,3)→(2,3)→(1,3);(3,1)→(2,1)→(2,2)→(2,3)→(1,3);(3,1)→(2,1)→(1,1)→(1,2)→(1,3))
思路拆解(四步曲套用)
第一步:定义状态
迷宫路径计数问题,且有障碍,因此定义:dp[i][j] = 从起点(m,1)走到(i,j)的不同路径数(dp[i][j] = 0表示不可达)。
目标是dp[1][n](出口位置)。
第二步:推导状态转移方程
只能向上或向右走,且只有空地(a[i][j] = 0)才能走:
- 若
a[i][j] = 1(树):dp[i][j] = 0(不可达);- 若
a[i][j] = 0(空地):走到(i,j)的前一步是(i+1,j)(从下方上来)或(i,j-1)(从左方过来),因此路径数是两者之和:dp[i][j] = (dp[i+1][j] + dp[i][j-1]) % 2333
第三步:初始化
起点是(m,1)(左下角),因此:
dp[m][1] = 1(起点本身有 1 种路径:原地不动);- 为了避免边界判断(比如
i=m时i+1越界,j=1时j-1越界),可以在矩阵下方加一行(i=m+1),左侧加一列(j=0),并将dp[m+1][1] = 0(下方无路径)、dp[m][0] = 0(左侧无路径),但更简单的方式是直接初始化dp[m][0] = 1(让dp[m][1] = dp[m+1][1](0) + dp[m][0](1) = 1)。
第四步:填表顺序
因为只能向上或向右走,且起点在(m,1)(下方),所以需要 “从下到上、从左到右” 填表:
- 从下到上:保证计算
dp[i][j]时,dp[i+1][j](下方)已计算;- 从左到右:保证计算
dp[i][j]时,dp[i][j-1](左侧)已计算。
代码实现(基础版:二维数组)
#include
using namespace std;
const int N = 3010; // m和n最大3000,开3010足够
const int MOD = 2333;
int m, n;
int a[N][N]; // 迷宫矩阵(1:树,0:空地)
int dp[N][N]; // dp[i][j]:走到(i,j)的路径数
int main() {
// 读取输入(注意:题目中迷宫的行是m行,列是n列)
scanf("%d%d", &m, &n); // 用scanf更快,避免超时
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
scanf("%d", &a[i][j]);
}
}
// 初始化:起点(m,1)的左侧dp[m][0] = 1,保证dp[m][1] = dp[m+1][1](0) + dp[m][0](1) = 1
dp[m][0] = 1;
// 填表:从下到上(i从m到1),从左到右(j从1到n)
for (int i = m; i >= 1; i--) {
for (int j = 1; j <= n; j++) {
// 如果是树,路径数为0
if (a[i][j] == 1) {
dp[i][j] = 0;
} else {
// 路径数 = 下方路径数 + 左侧路径数(取模)
dp[i][j] = (dp[i+1][j] + dp[i][j-1]) % MOD;
}
}
}
// 输出出口(1,n)的路径数
printf("%d\n", dp[1][n]);
return 0;
} 代码解析:为什么用scanf而不是cin?
因为
m和n最大 3000,矩阵规模是3000×3000 = 9e6,cin默认速度较慢,可能导致超时;scanf速度更快,能避免超时问题(实际编程中,遇到大数据量时建议用scanf/printf)。
优化:滚动数组(空间 O (mn)→O (n))
观察转移方程:dp[i][j]只依赖下方dp[i+1][j](上一行的j)和左侧dp[i][j-1](当前行的j-1),因此可用一维数组dp[j]存储,每次从下到上更新时,覆盖上一行的状态。
优化后代码:
#include
using namespace std;
const int N = 3010;
const int MOD = 2333;
int m, n;
int a[N][N];
int dp[N]; // 一维数组:dp[j]表示当前行第j列的路径数
int main() {
scanf("%d%d", &m, &n);
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
scanf("%d", &a[i][j]);
}
}
// 初始化:起点(m,1)的左侧dp[0] = 1
dp[0] = 1;
// 填表:从下到上(i从m到1),每行从左到右
for (int i = m; i >= 1; i--) {
// 处理当前行的第一个元素(j=1)
if (a[i][1] == 1) {
dp[1] = 0;
} else {
// 只能从下方(上一行的dp[1])过来
dp[1] = dp[1] % MOD;
}
// 处理当前行的其他元素(j>=2)
for (int j = 2; j <= n; j++) {
if (a[i][j] == 1) {
dp[j] = 0;
} else {
// dp[j](上一行的j,即下方路径数) + dp[j-1](当前行的j-1,即左侧路径数)
dp[j] = (dp[j] + dp[j-1]) % MOD;
}
}
}
printf("%d\n", dp[n]);
return 0;
} 优化解析
- 从下到上处理每行时,
dp[j]初始存储的是下一行(i+1)的dp[j](即下方路径数);- 处理当前行
j=1时,只能从下方过来,所以dp[1] = 下一行的dp[1](若为树则置 0);- 处理
j>=2时,dp[j] = 下一行的dp[j](下方) + 当前行的dp[j-1](左侧),取模后更新;- 空间从
O(mn)降至O(n),对于m=3e3、n=3e3的矩阵,内存占用从 9e6 降到 3e3,极大节省资源。
例题 4:过河卒(洛谷 P1002)—— 路径类 DP 的 “障碍 + 特殊约束题”
题目链接:https://www.luogu.com.cn/problem/P1002

题目描述:卒避马的路径计数
棋盘上A点(0,0)有一个过河卒,要走到B点(n,m),每次只能向下或向右走。棋盘上C点(x,y)有一匹马,马所在的点和马跳跃一步可达的点(共 9 个点)是 “控制点”,卒不能经过。求卒从A到B的不同路径数。
输入:一行四个整数n, m, x, y(1≤n,m≤20,0≤x,y≤20);
输出:路径数。
示例输入:
6 6 3 3示例输出:6(马在 (3,3),控制点覆盖周围 8 个点,卒需绕路走)
思路拆解(四步曲套用)
第一步:定义状态
卒的路径计数问题,且有 “马的控制点” 障碍,因此定义:dp[i][j] = 从(0,0)走到(i,j)的不同路径数(若(i,j)是控制点或越界,dp[i][j] = 0)。
目标是dp[n][m]。
第二步:推导状态转移方程
只能向下或向右走,且(i,j)必须不是控制点:
- 若
(i,j)是控制点:dp[i][j] = 0;- 若
(i,j)不是控制点:走到(i,j)的前一步是(i-1,j)(上方)或(i,j-1)(左侧),因此路径数是两者之和:dp[i][j] = dp[i-1][j] + dp[i][j-1]
第三步:初始化
- 起点
(0,0):若不是控制点,dp[0][0] = 1;若被马控制(比如马在 (0,0)),dp[0][0] = 0;- 边界处理:第一行(
i=0)只能从左向右走,若(0,j)不是控制点,dp[0][j] = dp[0][j-1];第一列(j=0)只能从上向下走,若(0,j)不是控制点,dp[i][0] = dp[i-1][0];- 马的控制点:需要先标记出所有控制点(马的位置
(x,y)+ 马跳一步的 8 个位置:(x±2,y±1)、(x±1,y±2))。
第四步:填表顺序
从左到右、从上到下(因为dp[i][j]依赖dp[i-1][j](上一行)和dp[i][j-1](左侧))。
代码实现(基础版:二维数组 + 控制点标记)
#include
#include // 用于abs函数
using namespace std;
typedef long long LL; // 路径数可能很大,用long long避免溢出
const int N = 25; // n和m最大20,开25足够
int n, m, x, y;
LL dp[N][N]; // dp[i][j]:走到(i,j)的路径数
// 判断(i,j)是否是马的控制点
bool is_control(int i, int j) {
// 马的位置:(x,y)
if (i == x && j == y) return true;
// 马跳一步的8个位置:dx和dy的组合是(±2,±1)、(±1,±2)
int dx = abs(i - x);
int dy = abs(j - y);
return (dx == 2 && dy == 1) || (dx == 1 && dy == 2);
}
int main() {
cin >> n >> m >> x >> y;
// 初始化:起点(0,0)
if (!is_control(0, 0)) {
dp[0][0] = 1;
} else {
dp[0][0] = 0;
}
// 初始化第一行(i=0,j从1到m)
for (int j = 1; j <= m; j++) {
if (!is_control(0, j)) {
dp[0][j] = dp[0][j-1]; // 只能从左向右
} else {
dp[0][j] = 0;
}
}
// 初始化第一列(j=0,i从1到n)
for (int i = 1; i <= n; i++) {
if (!is_control(i, 0)) {
dp[i][0] = dp[i-1][0]; // 只能从上向下
} else {
dp[i][0] = 0;
}
}
// 填表:从左到右,从上到下
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (is_control(i, j)) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
cout << dp[n][m] << endl;
return 0;
} 代码解析:为什么用long long?
当
n和m为 20 时,最大路径数是C(40,20) ≈ 137846528820,远超int的最大值(约 2e9),因此必须用long long存储,避免溢出。
优化:边界统一处理(避免单独初始化第一行 / 列)
和 “矩阵最小路径和” 类似,我们可以将dp数组的规模扩大一行一列(dp[0..n+1][0..m+1]),并将dp[1][0] = 1(起点(0,0)对应dp[1][1]),这样可以统一转移方程,不需要单独初始化第一行和第一列。
优化后代码:
#include
#include
using namespace std;
typedef long long LL;
const int N = 25;
int n, m, x, y;
LL dp[N][N];
bool is_control(int i, int j) {
// 注意:这里i和j是扩大后的坐标,需要减1对应原坐标
i--; j--;
if (i == x && j == y) return true;
int dx = abs(i - x);
int dy = abs(j - y);
return (dx == 2 && dy == 1) || (dx == 1 && dy == 2);
}
int main() {
cin >> n >> m >> x >> y;
// 扩大坐标:原(0,0)对应(1,1),dp[1][0] = 1(前序状态)
dp[1][0] = 1;
// 填表:从左到右,从上到下(i从1到n+1,j从1到m+1)
for (int i = 1; i <= n+1; i++) {
for (int j = 1; j <= m+1; j++) {
// 跳过起点的前序状态(i=1,j=0已处理)
if (i == 1 && j == 0) continue;
// 判断当前扩大后的坐标是否是控制点
if (is_control(i, j)) {
dp[i][j] = 0;
} else {
// 统一转移方程:dp[i-1][j](上方) + dp[i][j-1](左侧)
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
// 原(n,m)对应扩大后的(n+1,m+1)
cout << dp[n+1][m+1] << endl;
return 0;
} 优化解析
- 扩大坐标后,原坐标
(i,j)对应新坐标(i+1,j+1),这样可以避免i=0或j=0时的越界判断;dp[1][0] = 1:保证新坐标(1,1)(原(0,0))的路径数为dp[0][1](0) + dp[1][0](1) = 1;- 统一转移方程后,不需要单独初始化第一行和第一列,代码更简洁。
三、路径类 DP 通用解题模板总结
通过以上 4 道例题,我们可以总结出路径类 DP 的通用解题模板,以后遇到这类题,直接套用即可:
1. 问题分析
- 确定地图结构:是二维矩阵、三角形、还是迷宫?
- 确定移动方向:只能向右 / 向下 / 向上 / 向左,或多方向?
- 确定目标:求最小 / 最大路径和、路径数,还是带约束的路径?
- 确定障碍:是否有不可达区域(如树、马的控制点)?
2. 状态定义
- 二维状态:
dp[i][j]= 走到(i,j)的目标值(路径和 / 路径数);- 一维状态(优化后):
dp[j]= 当前行第j列的目标值。
3. 转移方程推导
- 无障碍 + 单方向(右 / 下):
dp[i][j] = min/max/sum(dp[i-1][j], dp[i][j-1]) + 权重(如矩阵元素);- 有障碍:先判断
(i,j)是否可达,可达则按无障碍推导,不可达则dp[i][j] = 0(计数)或无穷大(最值);- 多方向(上 / 右):调整填表顺序(如从下到上),确保依赖的前序状态已计算。
4. 初始化
- 起点初始化:
dp[起点坐标] = 1(计数)或起点权重(路径和);- 边界初始化:第一行 / 列按移动方向单独初始化,或扩大数组规模统一处理;
- 障碍初始化:标记所有不可达区域,初始化为 0 或无穷大。
5. 填表顺序
- 右 / 下方向:从左到右、从上到下;
- 上 / 右方向:从下到上、从左到右;
- 优化版(一维数组):根据依赖关系确定遍历方向(如从右向左避免覆盖)。
6. 优化技巧
- 空间优化:用一维数组替代二维数组(滚动数组),空间复杂度从
O(nm)降至O(m);- 时间优化:提前标记障碍,避免填表时重复判断;用
scanf/printf处理大数据量;- 边界优化:扩大数组规模,统一转移方程,避免单独处理第一行 / 列。
总结
路径类 DP 作为线性 DP 的重要分支,本质是 “用位置定义状态,用方向推导转移”。它的难点不在于逻辑复杂,而在于 “状态设计的合理性” 和 “边界处理的严谨性”—— 比如如何定义
dp[i][j]才能让转移方程自然成立,如何处理障碍和越界避免逻辑漏洞。最后,给大家一个小建议:刷题时不要急于看题解,先尝试自己套用 “四步曲”—— 先定义状态,再推导转移方程,最后写代码验证。遇到错误时,先检查状态定义是否合理,再看转移方程是否覆盖所有情况,最后排查边界和填表顺序。
路径类 DP 是后续学习更复杂 DP(如区间 DP、树形 DP)的基础,打好这个基础,后面的学习会事半功倍。希望这篇 5000 字的保姆级教程,能帮你彻底吃透路径类线性 DP,在算法路上更上一层楼!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号