
(以下内容全部来自上述课程)
大纲

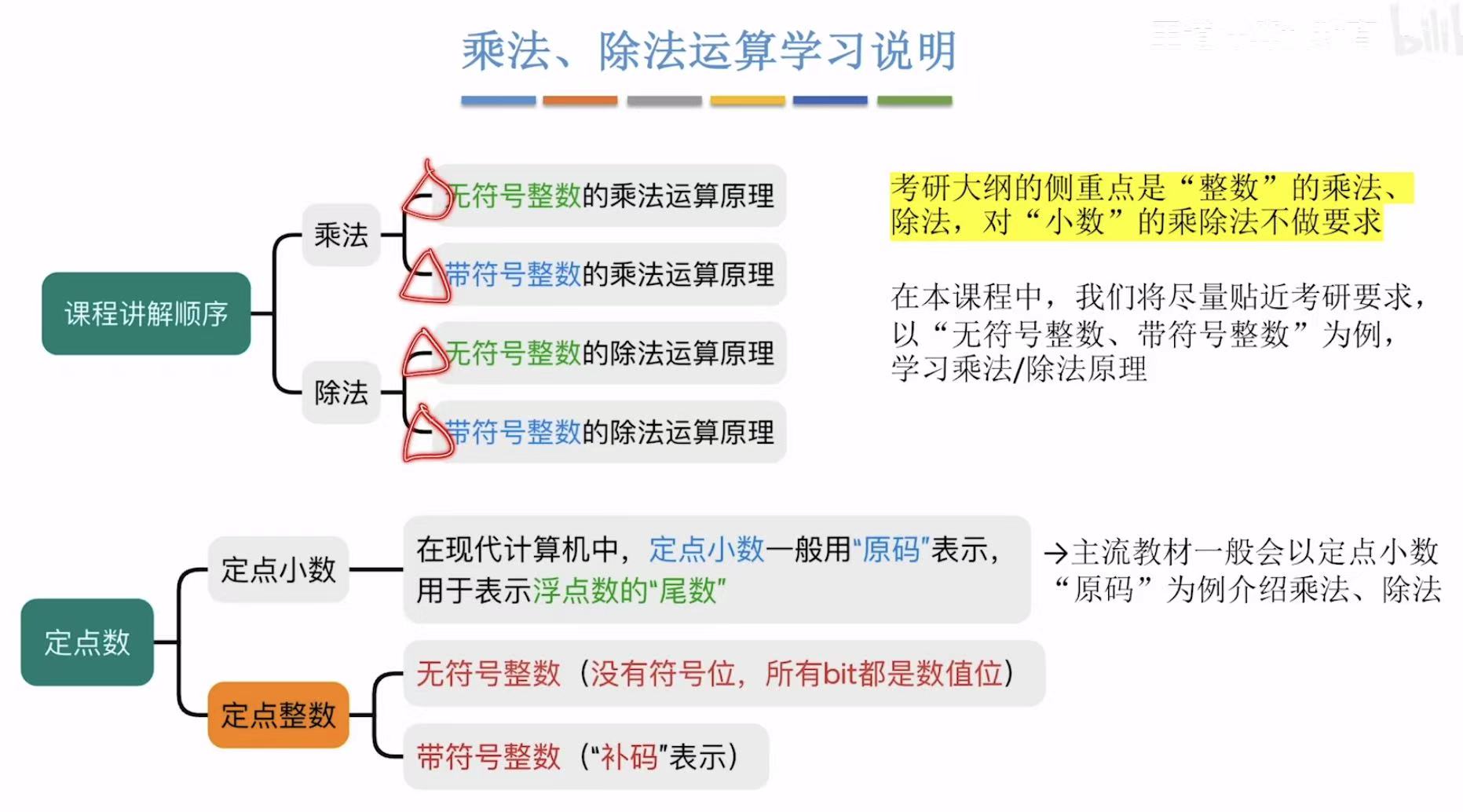
无符号整数的乘法运算原理
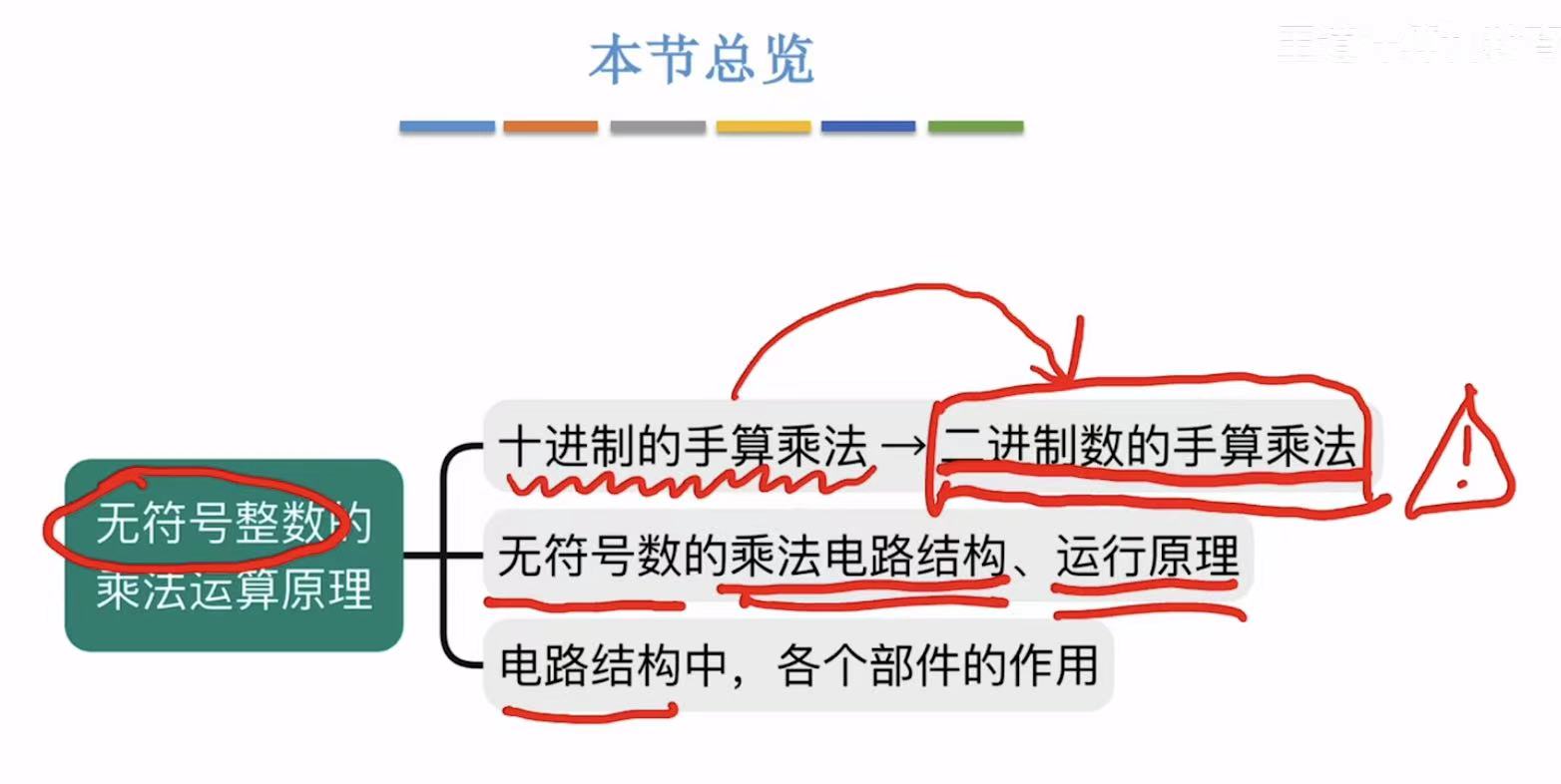
1. 手算乘法
错位:相当于省略了后边儿需要补的0。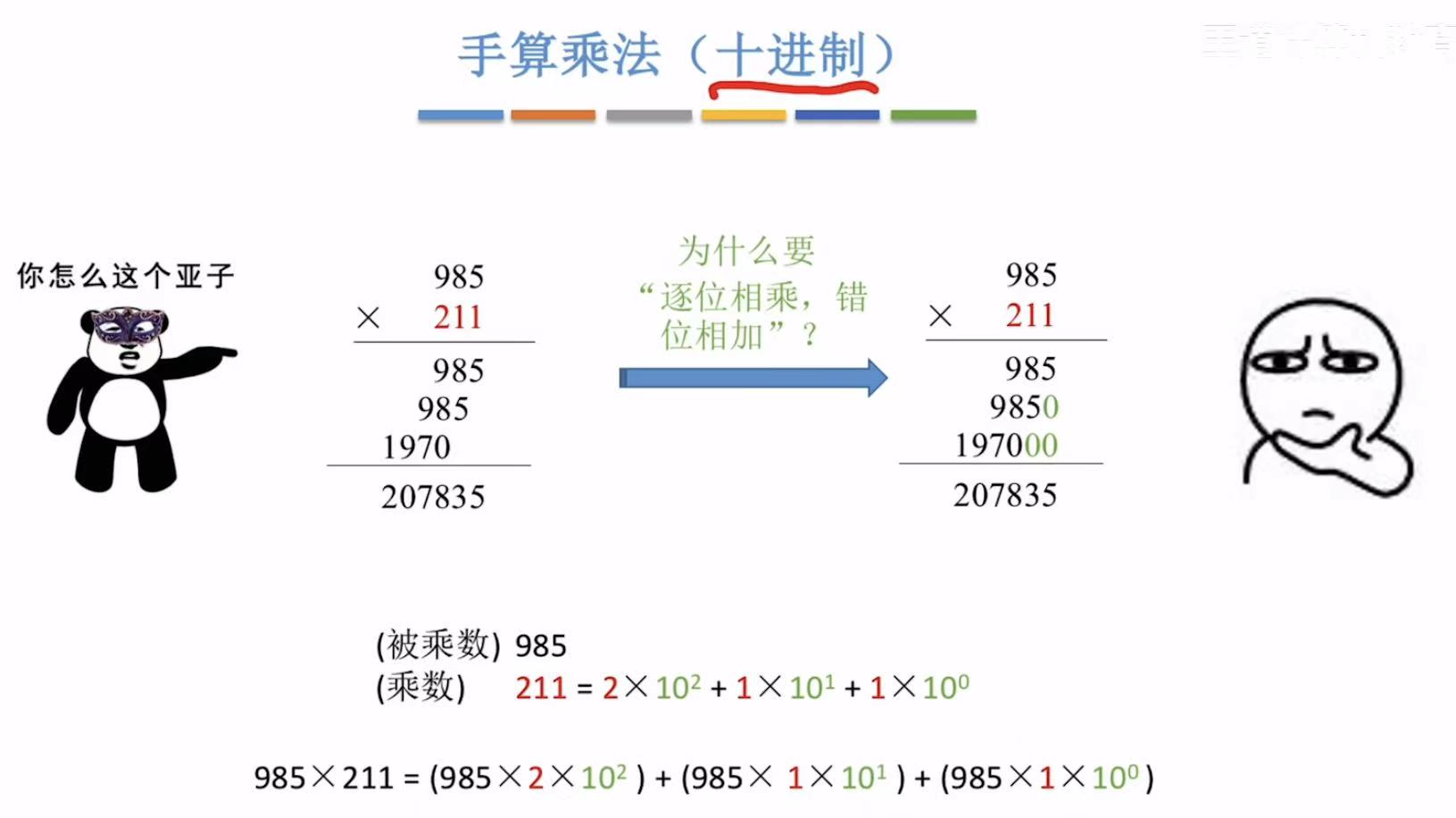
从十进制同理可得,二进制正常的乘法计算也必须错位相加。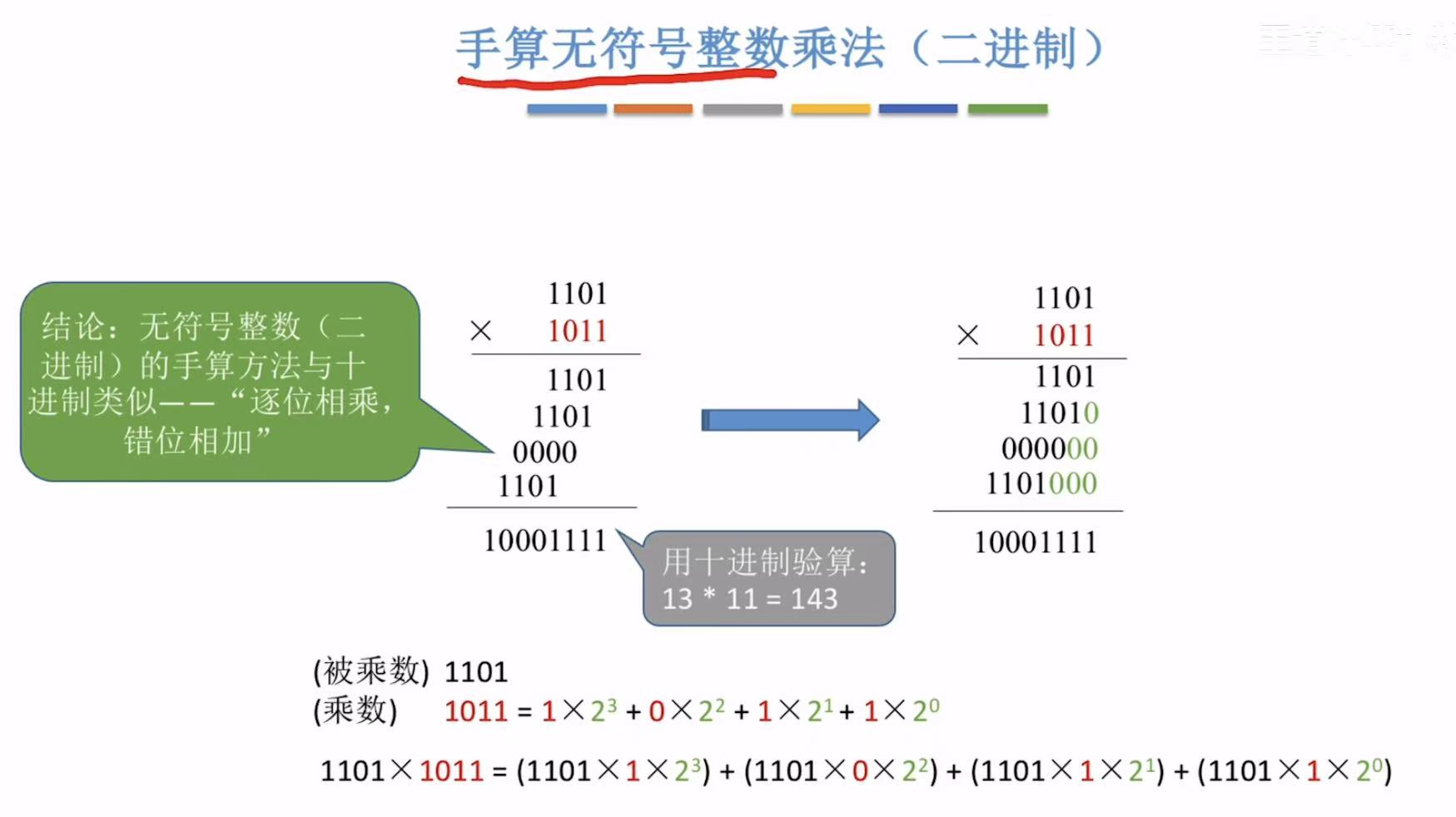
1101*0=0000
因为我们要搞清怎么用硬件计算,所以引入了部分积的概念,更好地理清计算的过程。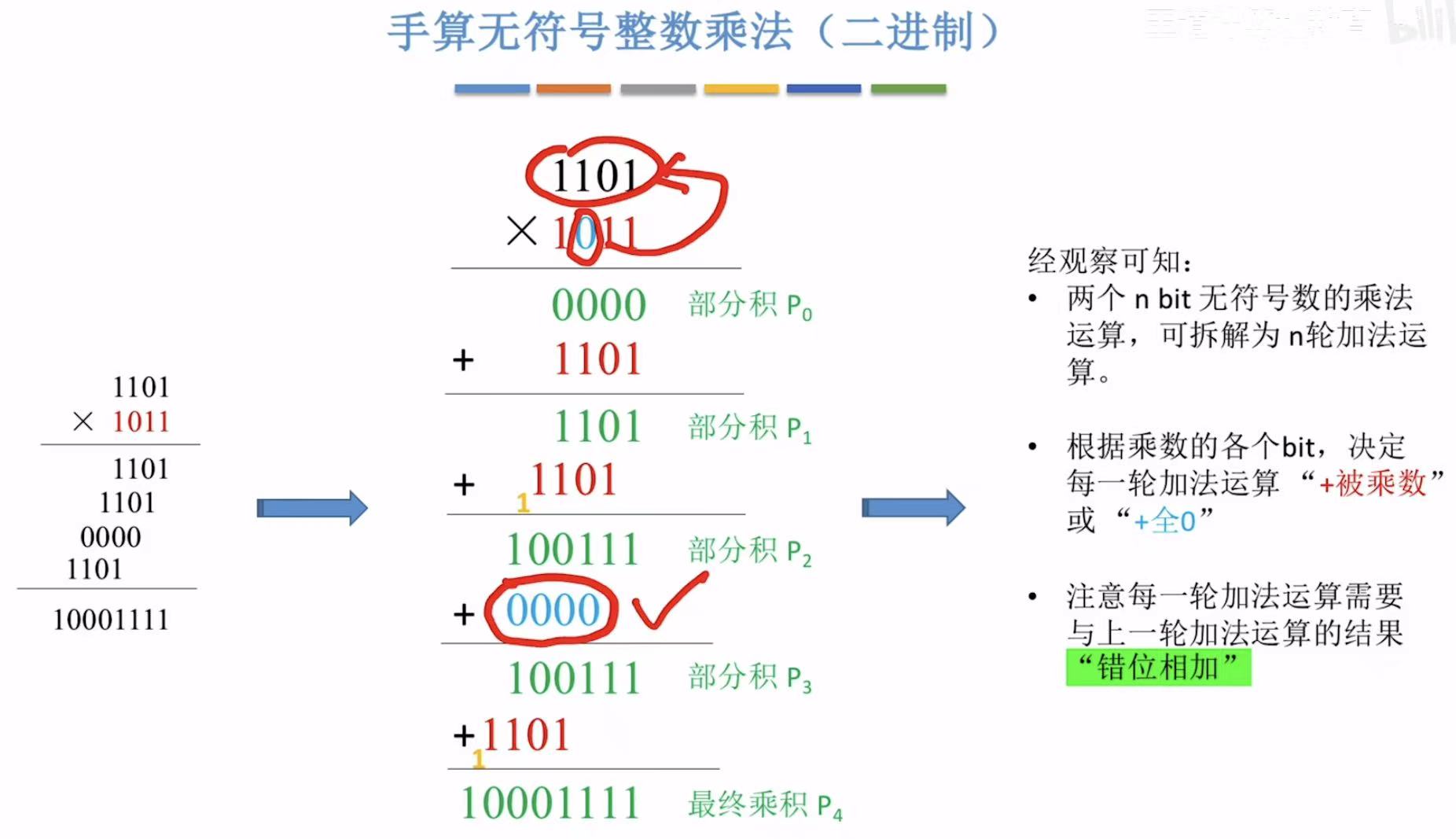
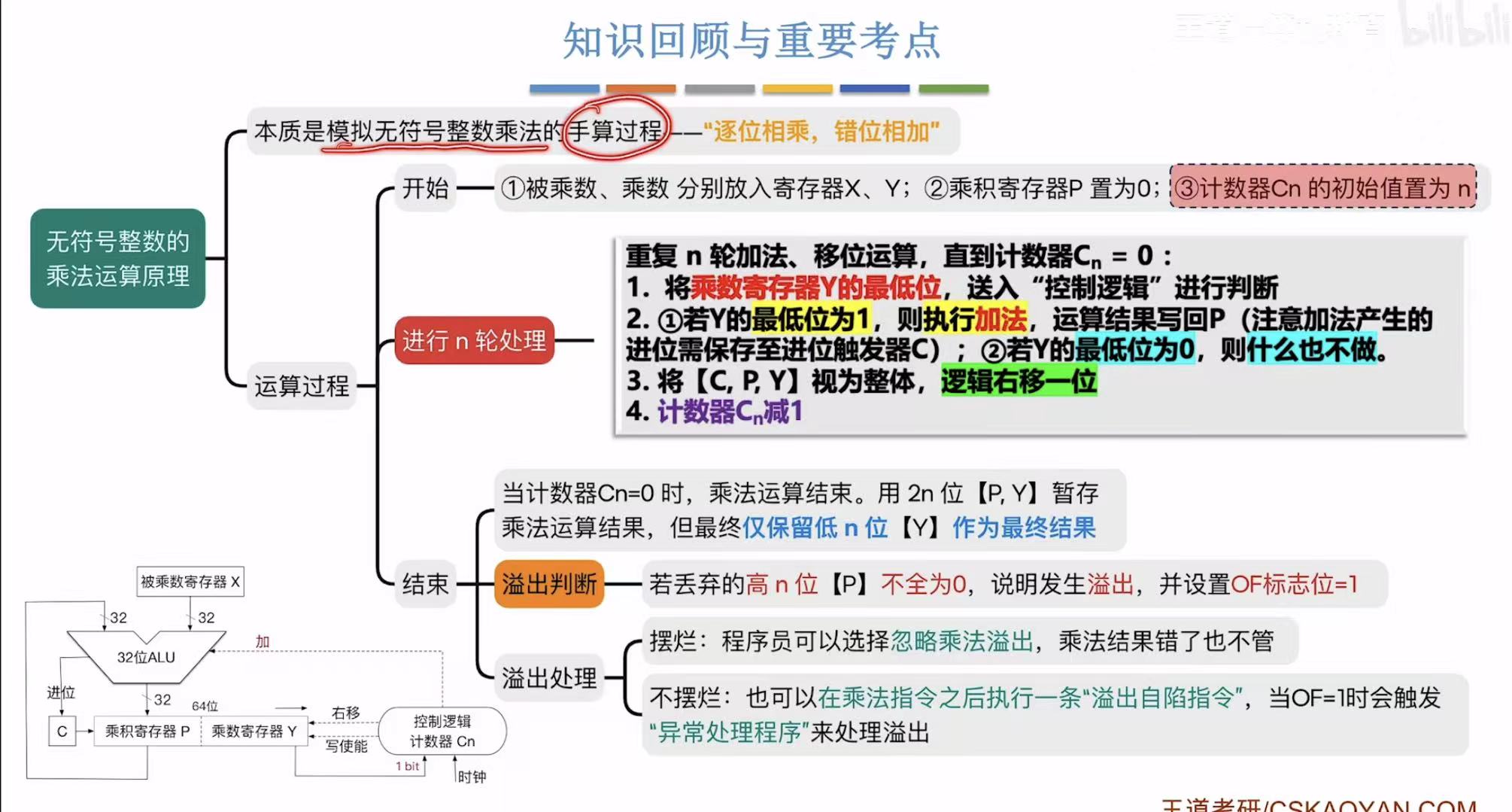
2. 乘法原理
2.1 n轮运算
n=乘数的位数
第一步就是各就各位,把数字全部放进去。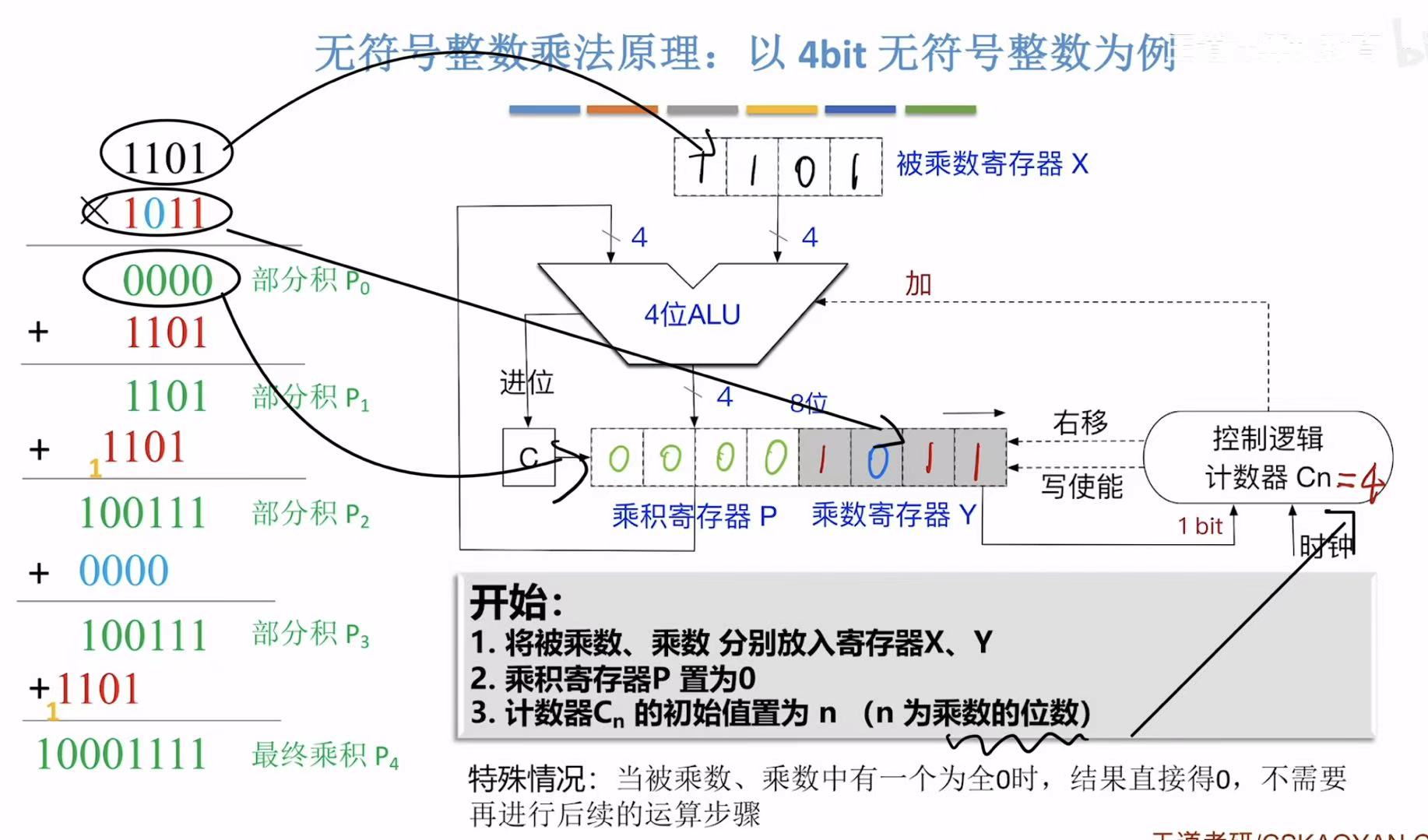
第一轮循环:
- 寄存器最低为为1–>控制逻辑判断执行加法–>P+X–>结果写回P–>CPY视为一体,向右移动一位–>出去的那一位舍弃
- 如图:1–>加法–>1101+0000–>PY=11011011–>CPY=011011011–>右移–>01101101–>n=3
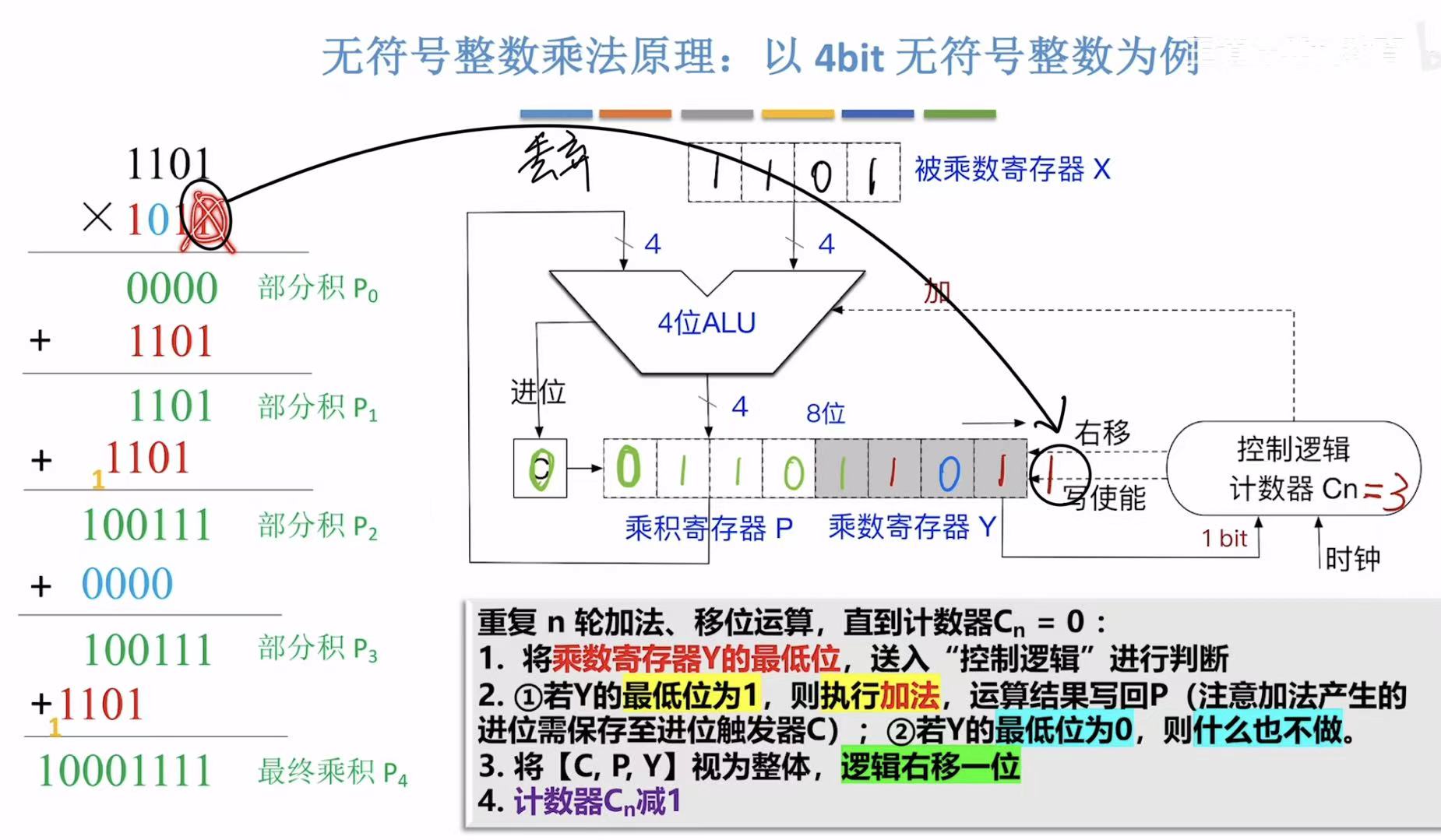
下一轮P+X就如图左面红圈里显示的一样,P一直都是部分积,X一直是被乘数。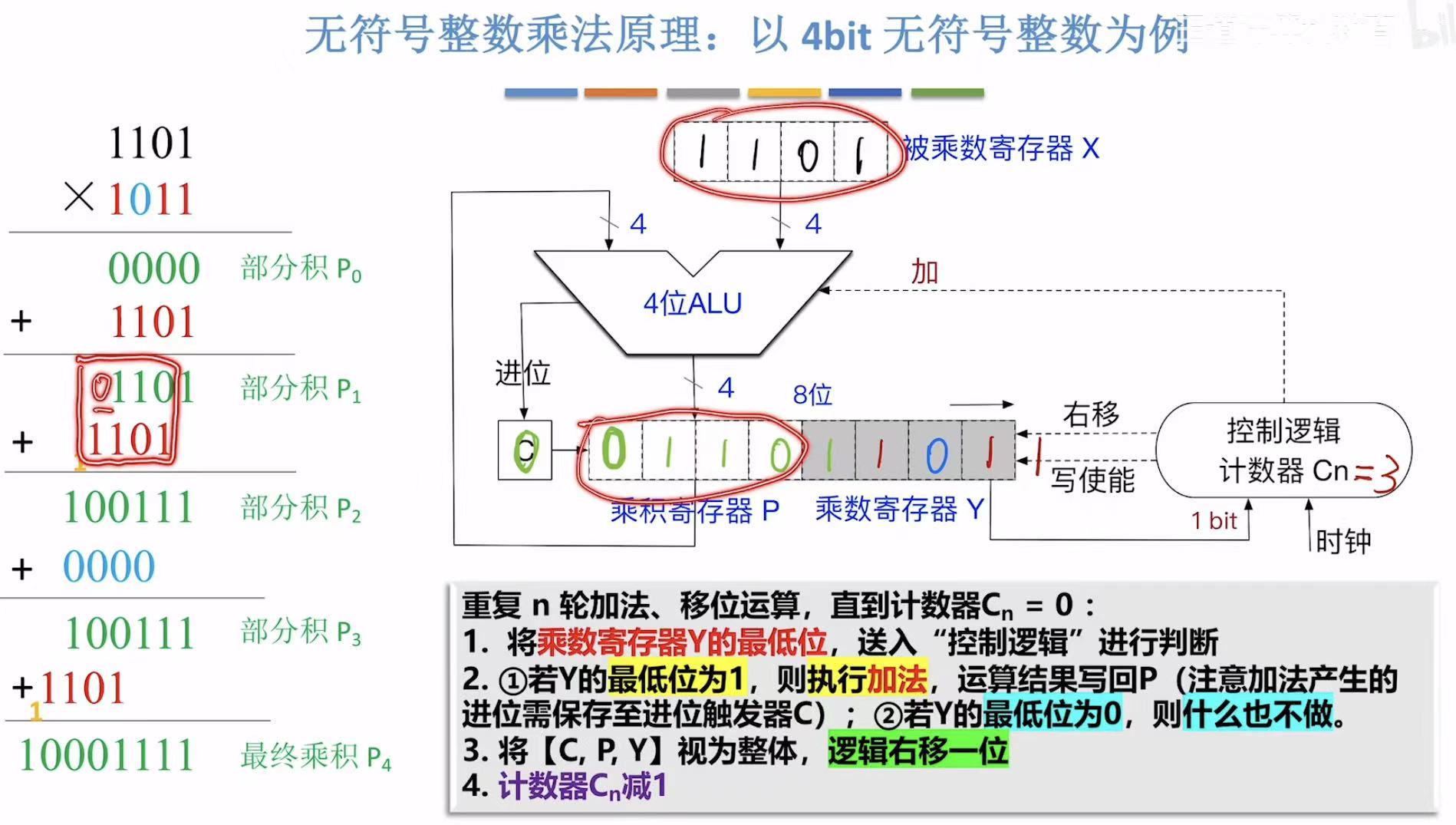
Y最低位为0:
先CPY一体向右移动一位=00110110,因为有进位,所以此时C赋值为1,合起来就是竖式中的10011,与此同时,前面的CPY最后一位刚好是0,所以什么也不用做(对应蓝色字部分),不需要进行加法操作,直接下一步CPY一体向右移动一位即可。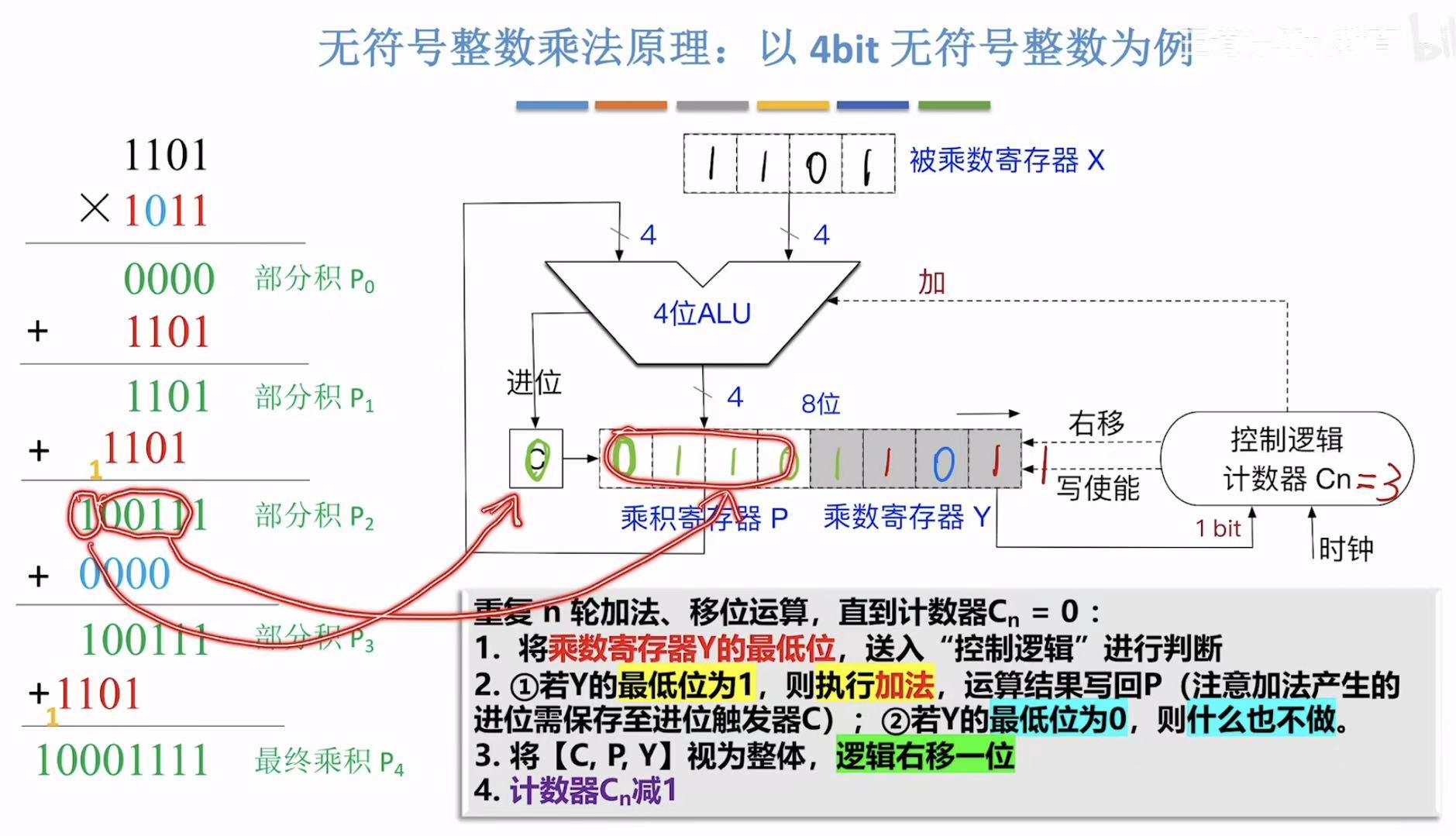
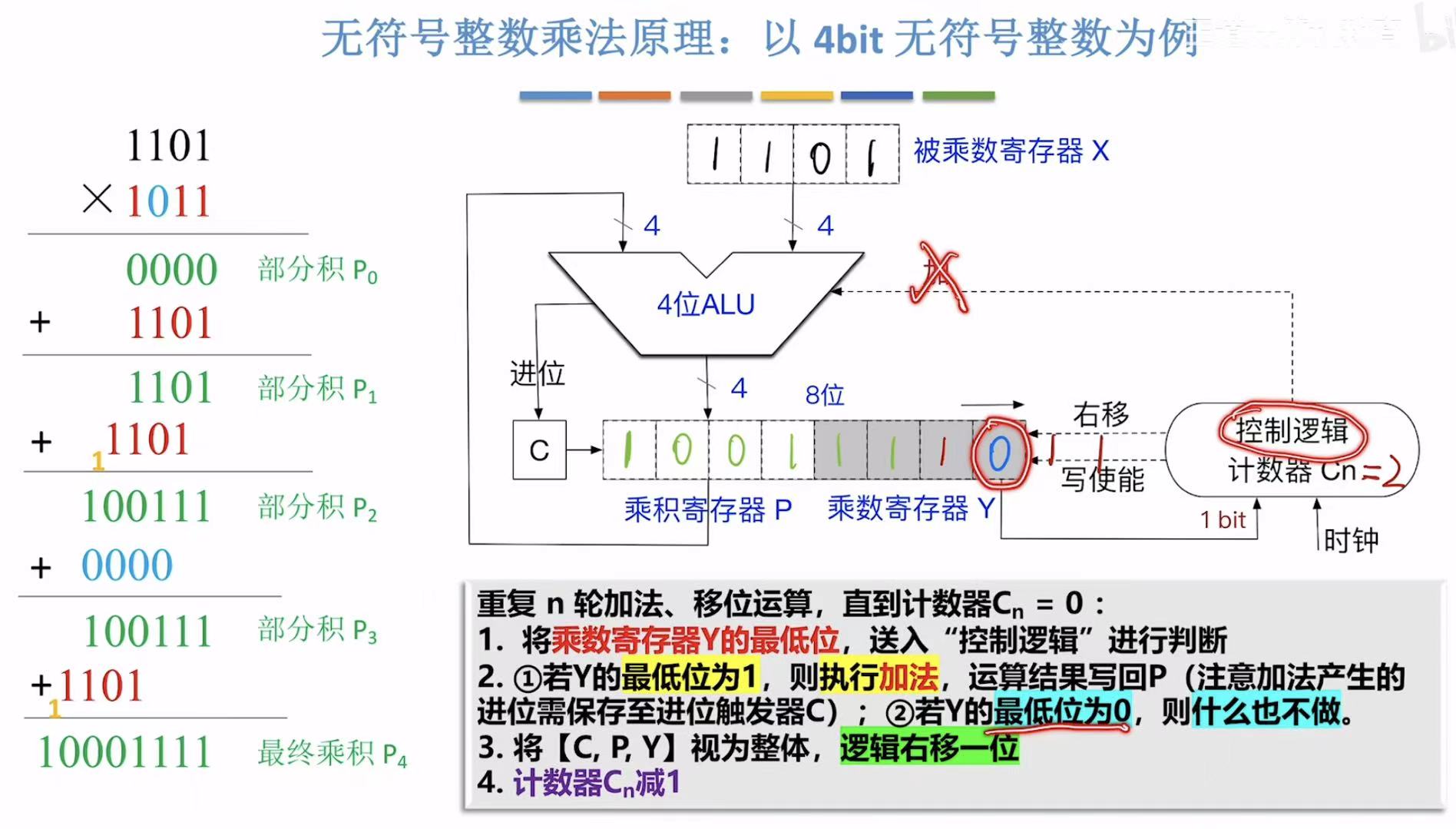
最后刚好写入寄存器中的结果就是算出来的这八位数字。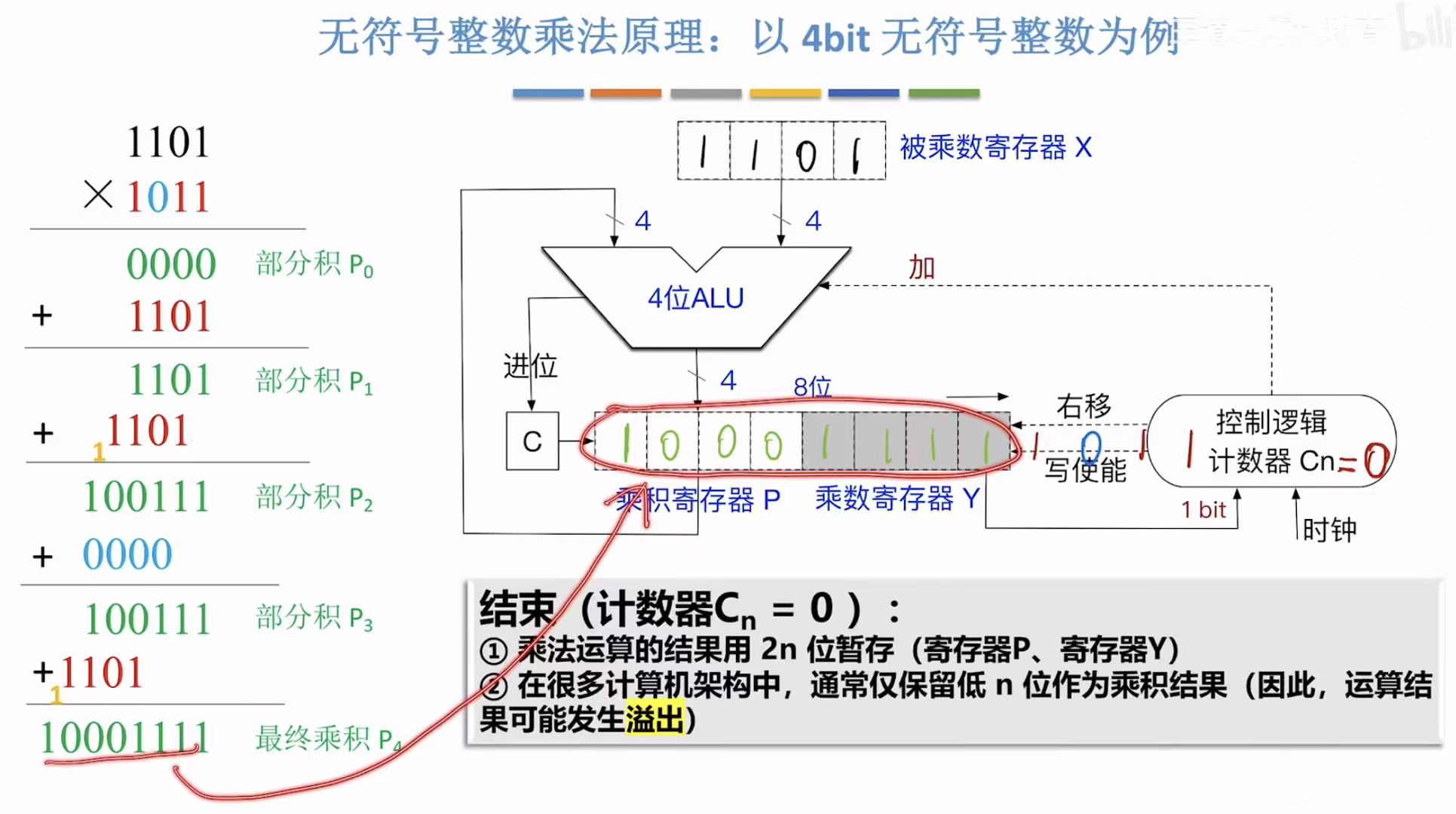
因为很多计算机中只会保留后四位,我们算出来的结果是八位,前面都是零就没差异,如果不是的话,就和我们整体的数字有差异,人家只要四位,我们有八位,所以此种情况就叫做溢出。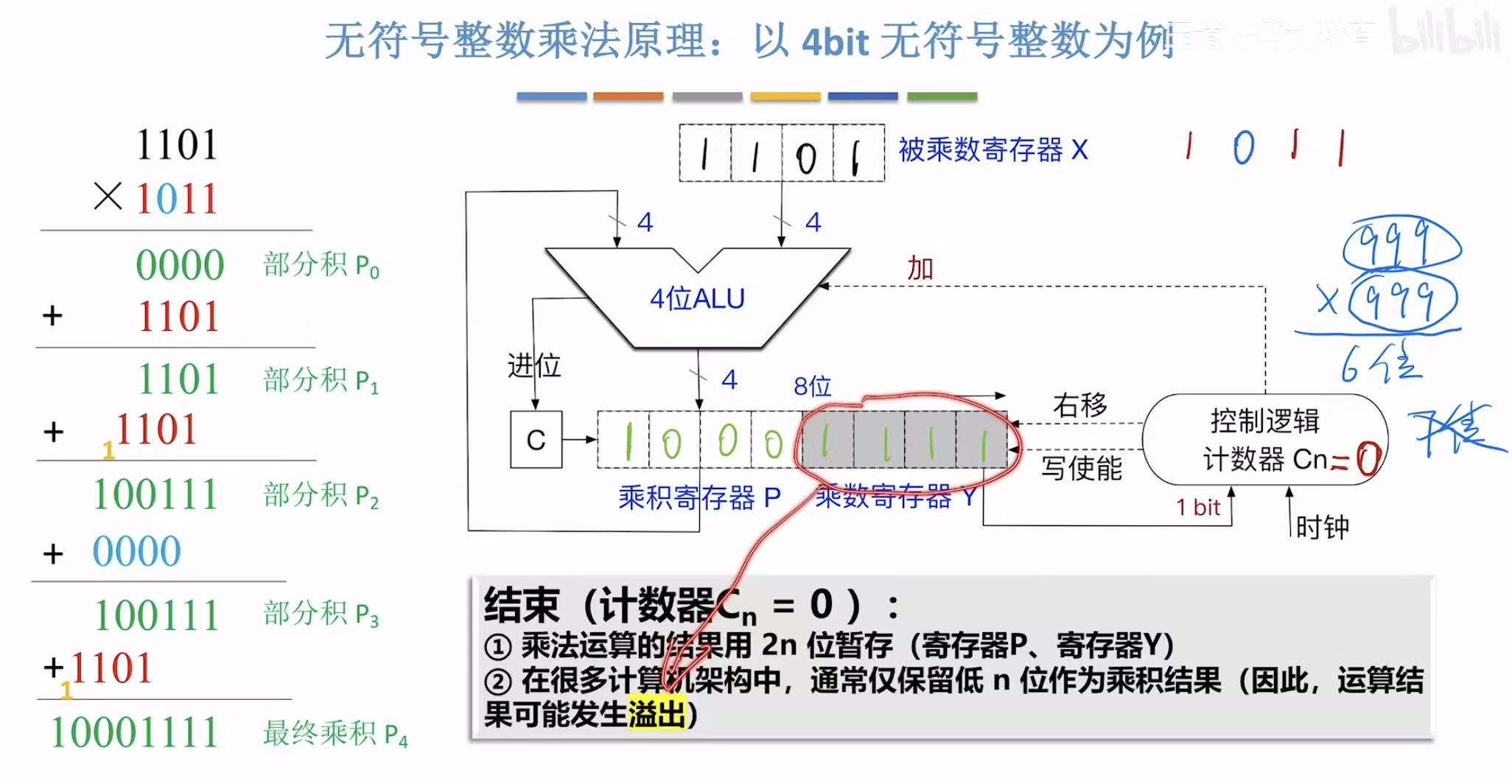
2.2 溢出判断及处理
要想处理溢出,就要先知道它到底有没有溢出,然后才能解决,所以我们就需要先标记溢出–>OF标志位。
过程:溢出–>OF==1–>异常处理程序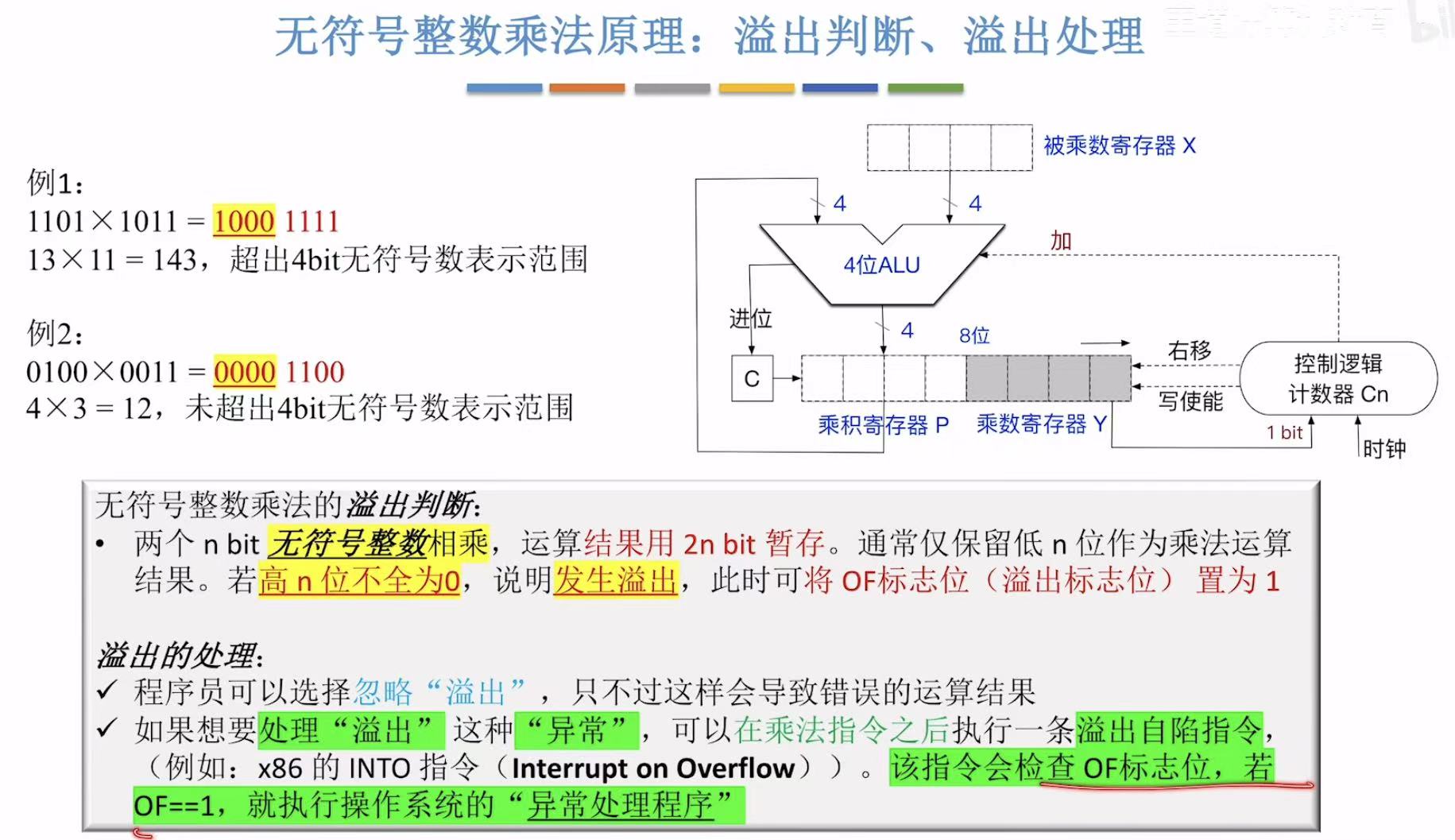
3. 32位乘法运算电路
过程和4位的一模一样,只不过位数变多了而已。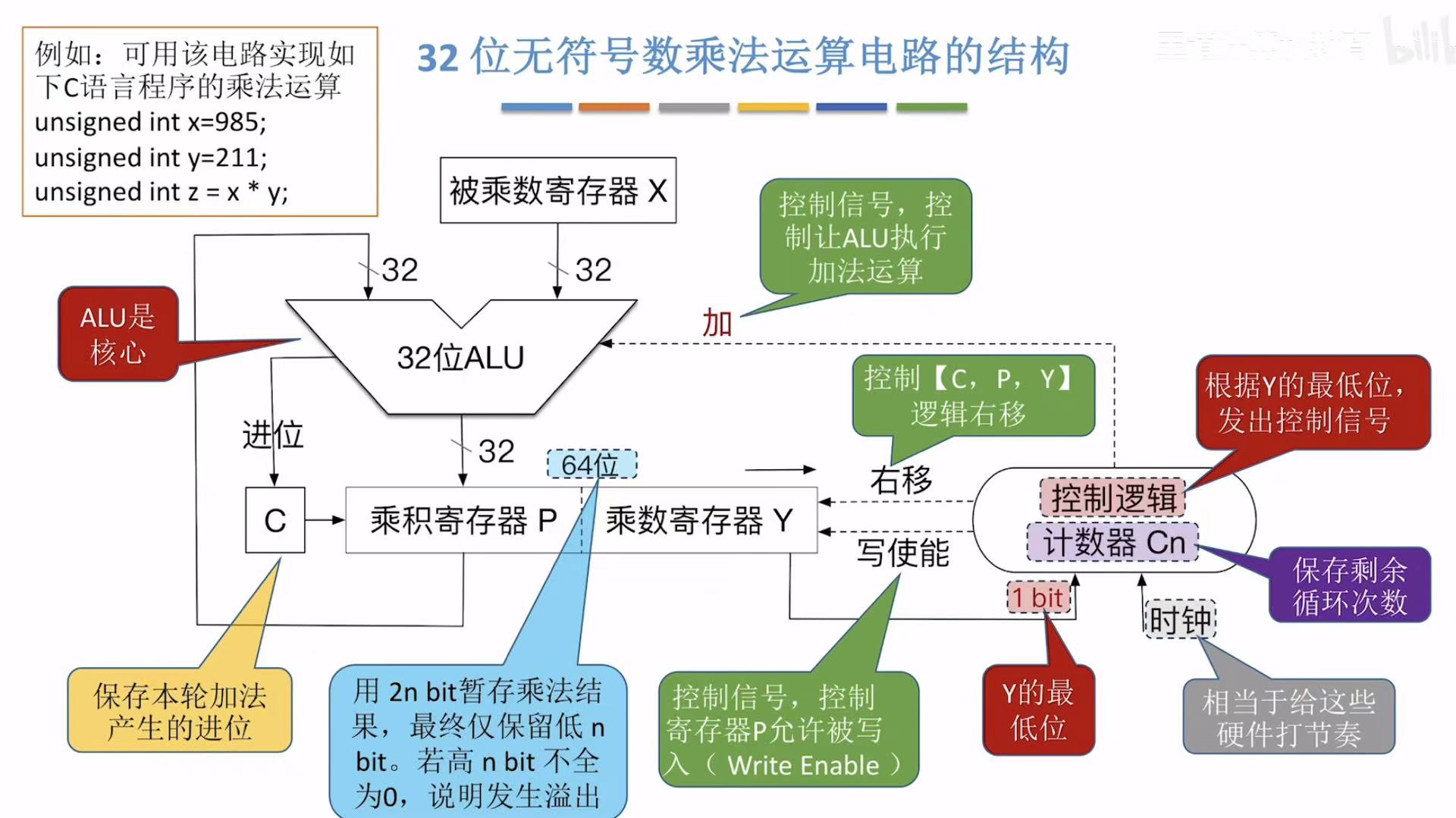
4. 小结
带符号整数的乘法运算原理
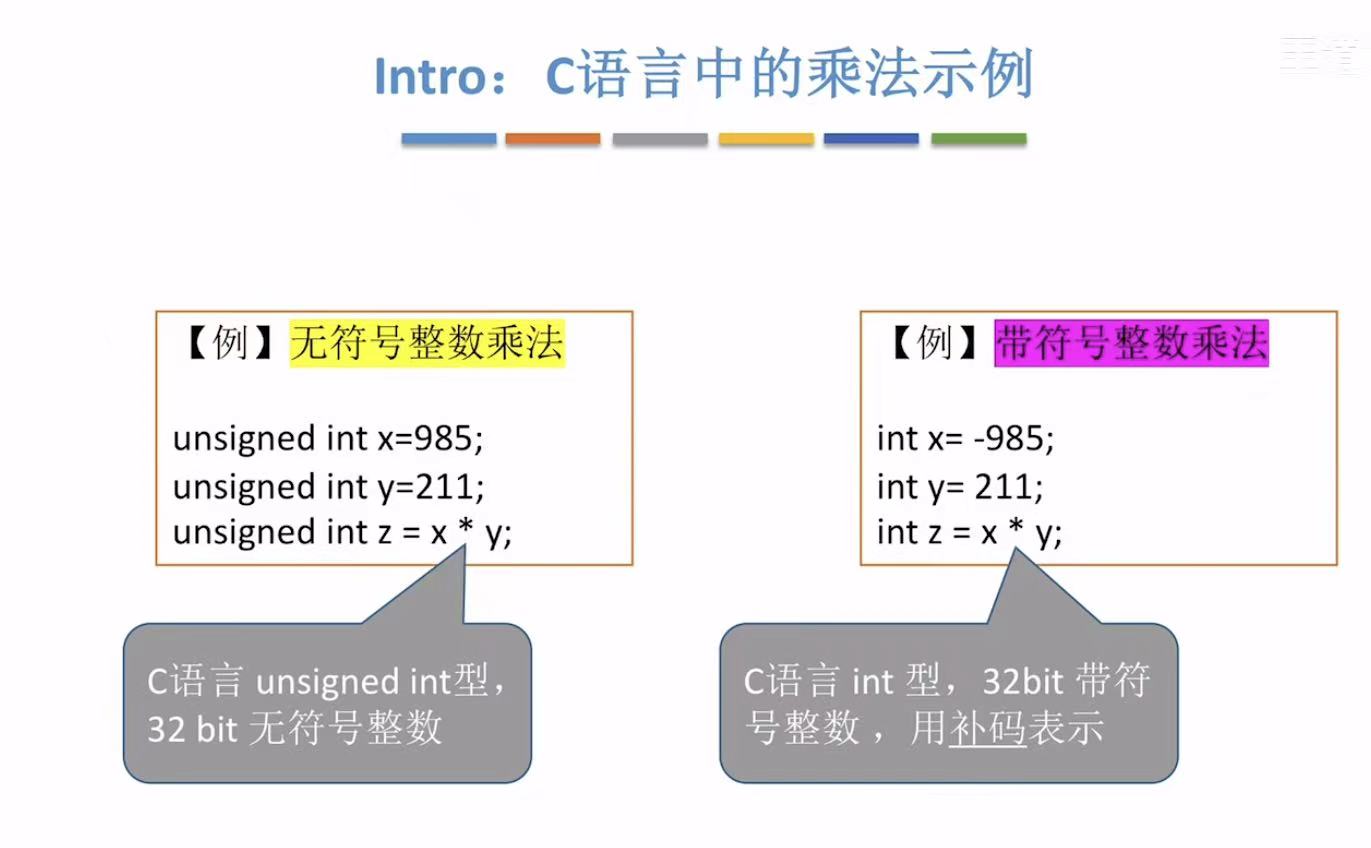
C语言中的乘法示例:
1. 对比
如果带符号的乘法也用无符号的电路计算的话:
嗯,很明显是错的。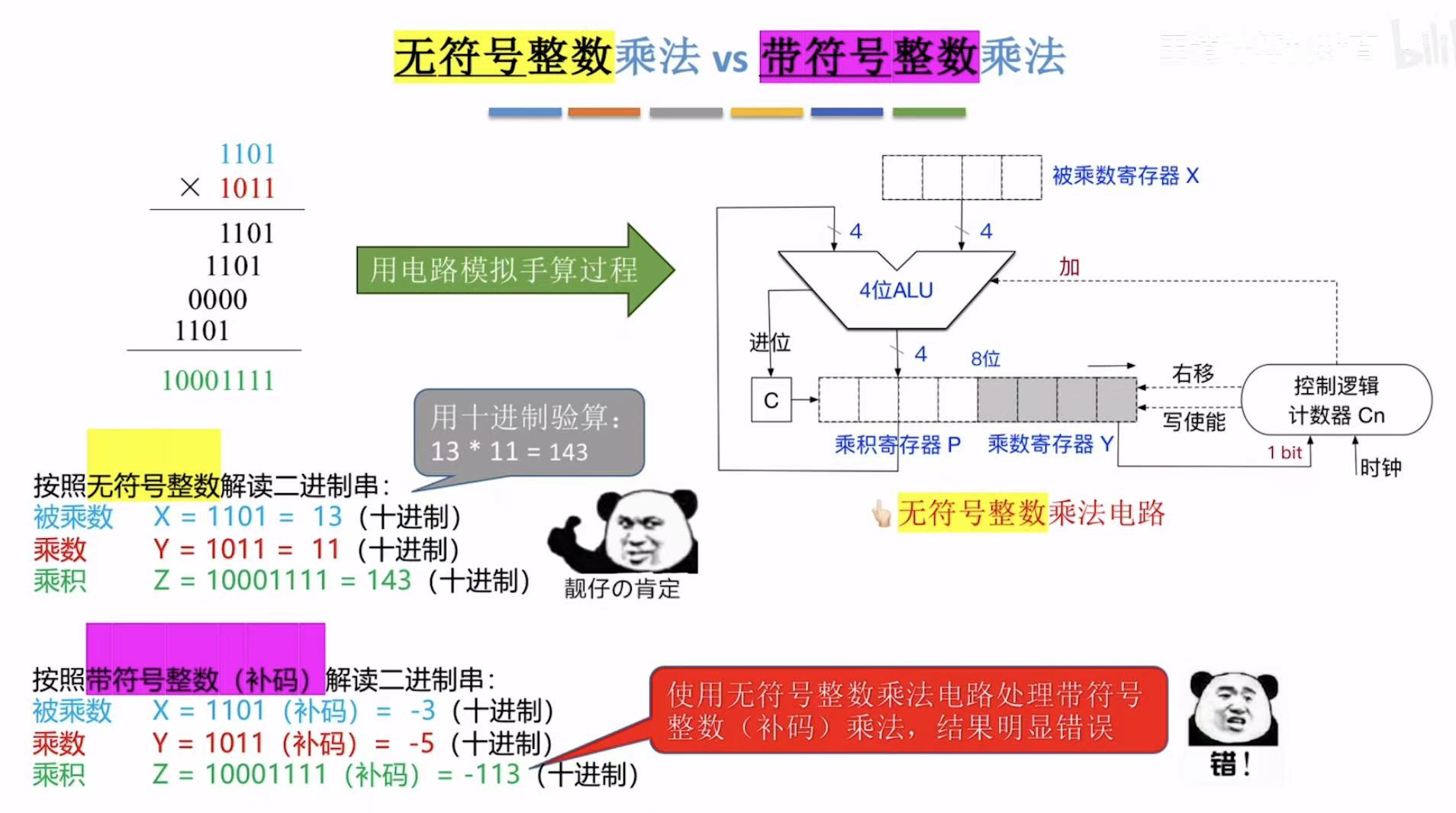
无符号的乘法电路无法满足带符号的乘法需求,所以在无符号的基础上进行了改进。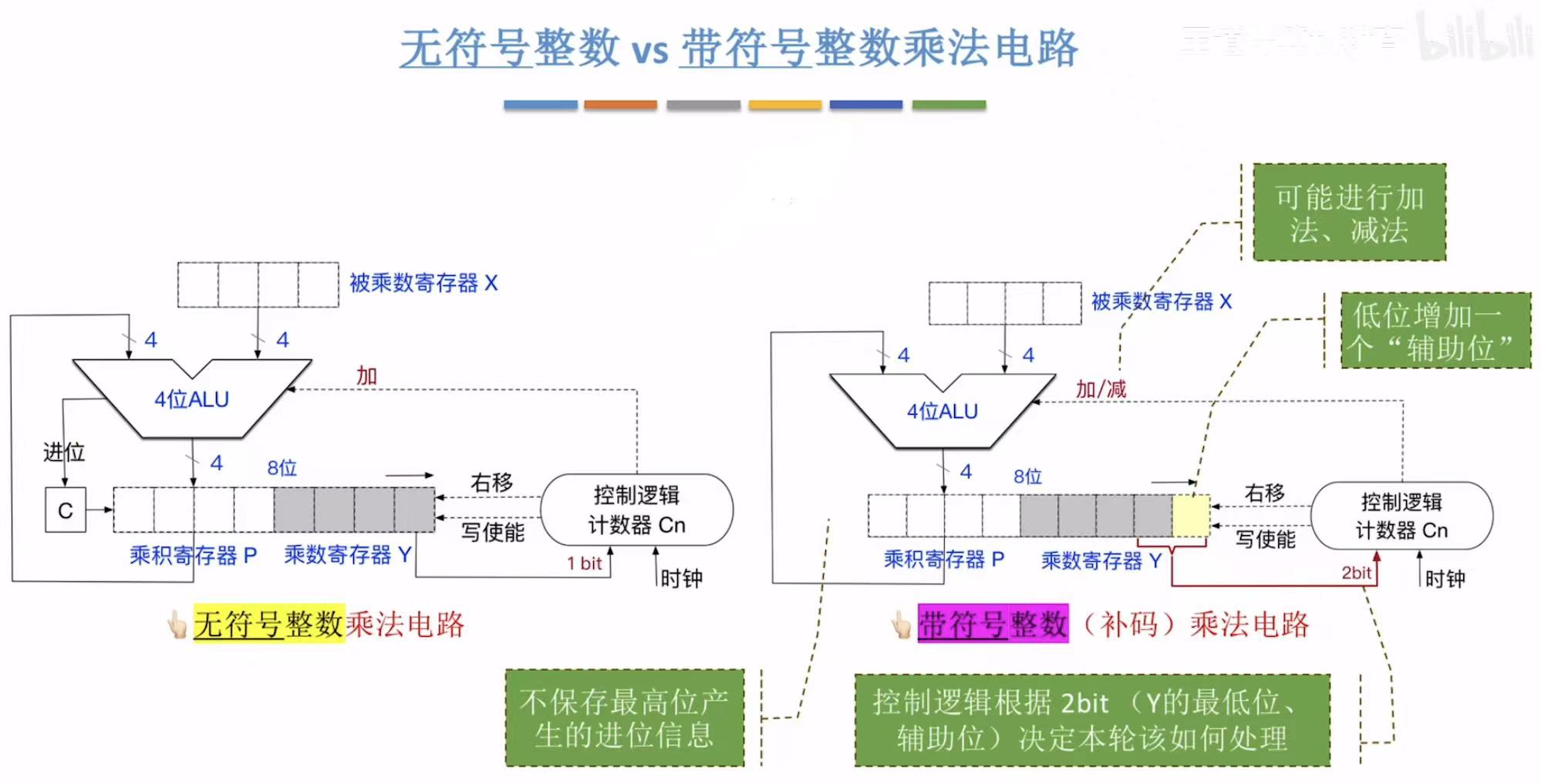
2. 乘法原理
2.1 n轮运算
和无符号的过程一样,第一步都是各就各位,数字都到自己该去的位置。
注意这里的特殊情况,一个乘数等于0,就直接输出0的结果,用不着继续运算了。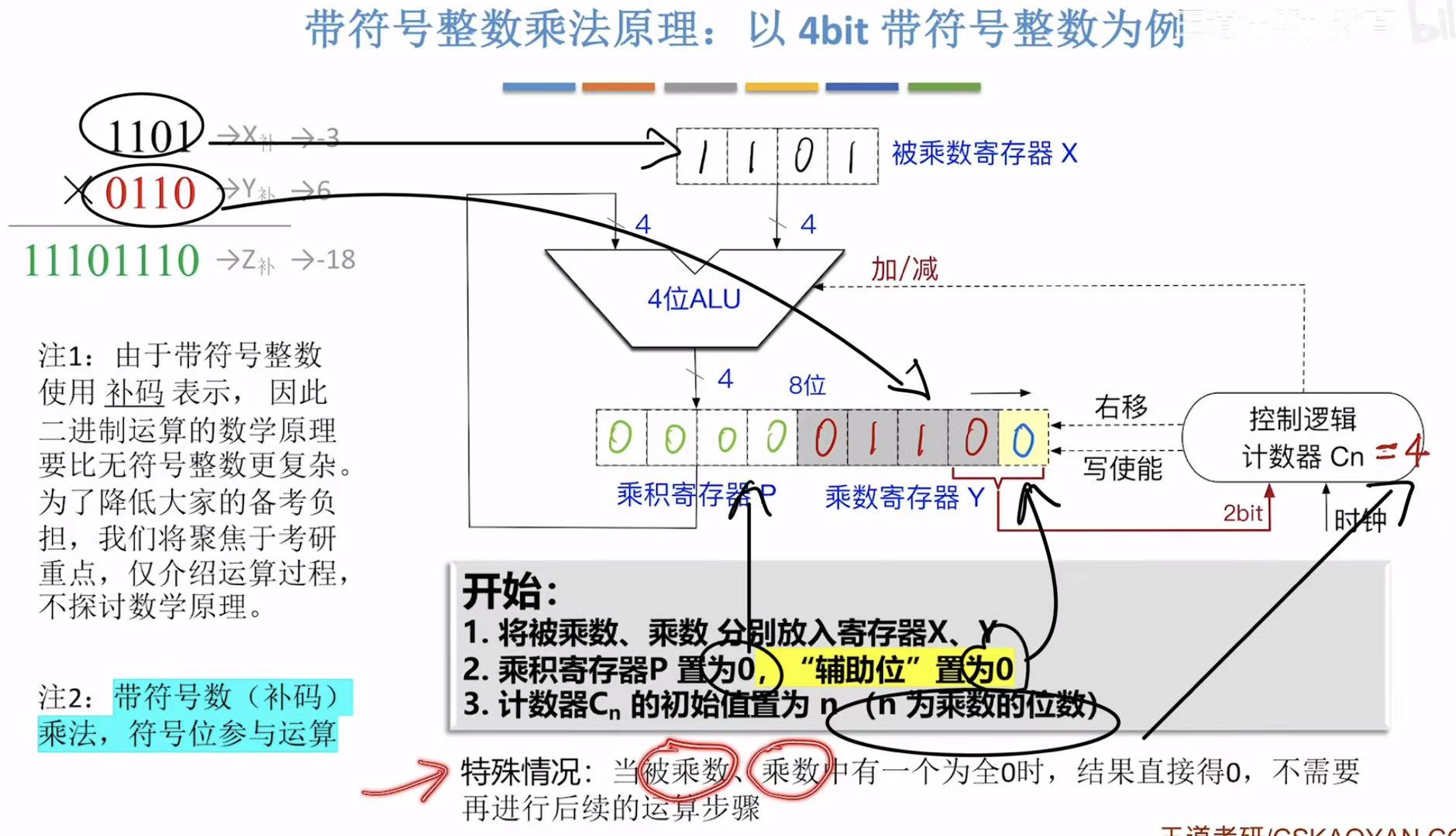
大体上和无符号的过程一直,我们来看看不一样的地方:
这里用PY的后两位来进行判断到底是该进行加法操作还是减法操作。
轻松记忆(异或):
- 00:相同就是不变
- 01:不相同就是需要改变,0在前,当0表示符号的时候是正数,所以就是加法操作
- 10:不相同就是需要改变,1在前,当1表示符号的时候是负数,所以就是减法管理
- 不变就是11:相同就
此时:
- 缘于最开始的PY辅助位的最后两位是00,所以没有改变,就直接向右移动一位,把0移出来了。
- 接下来,最终两位变为10,就需要进行-x[补]的操作(见下一个图)
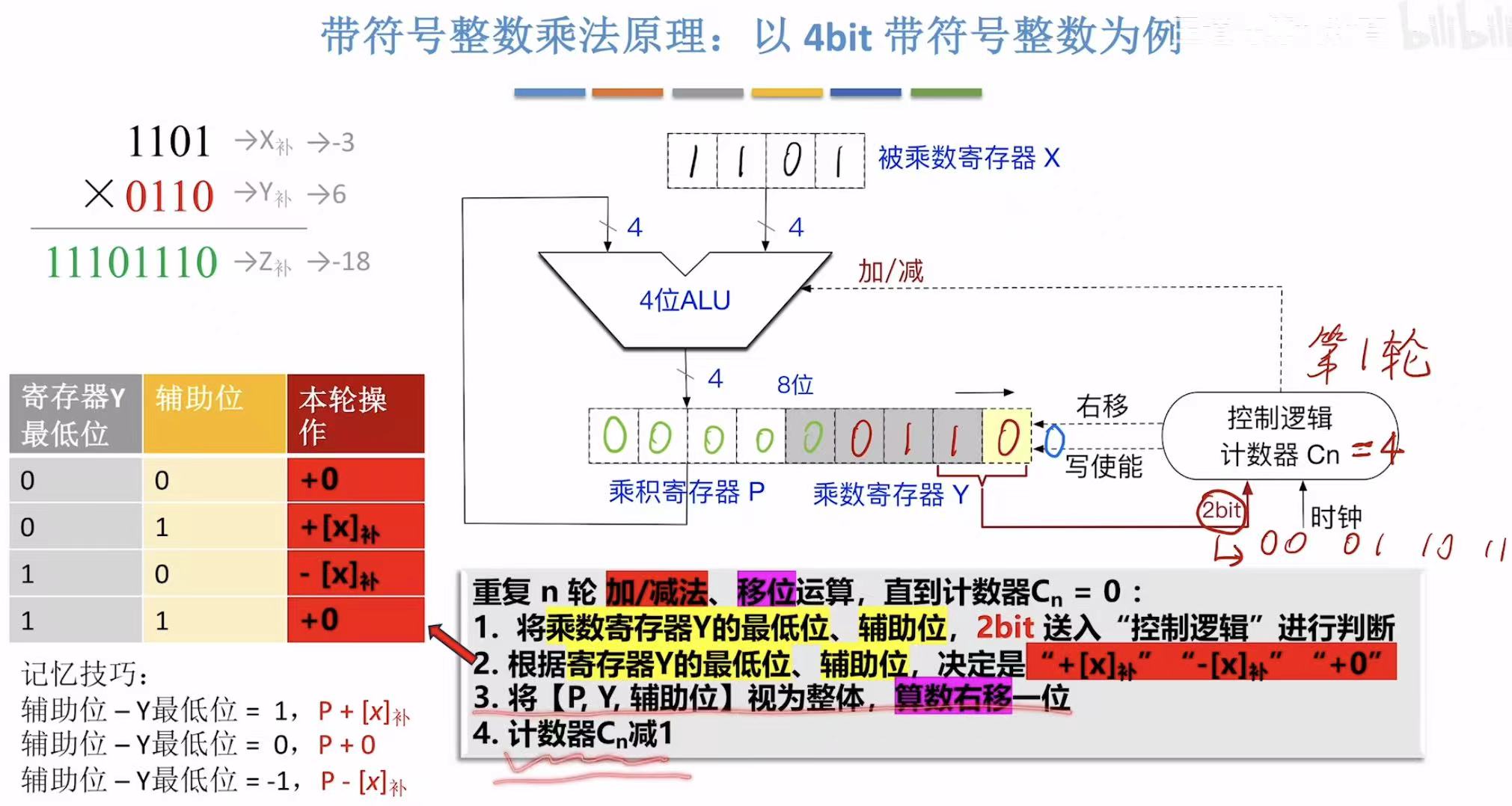
书接上文: - 见右上角的-x[补]的操控,所以放回寄存器,此时的PY辅助位=001100110,右移=空00110011,0被挤出去
- 这个空就是它后边儿的那位数,
空0,所以空就补一个0上去。 - 此时的PY辅助位=000110011(如图)
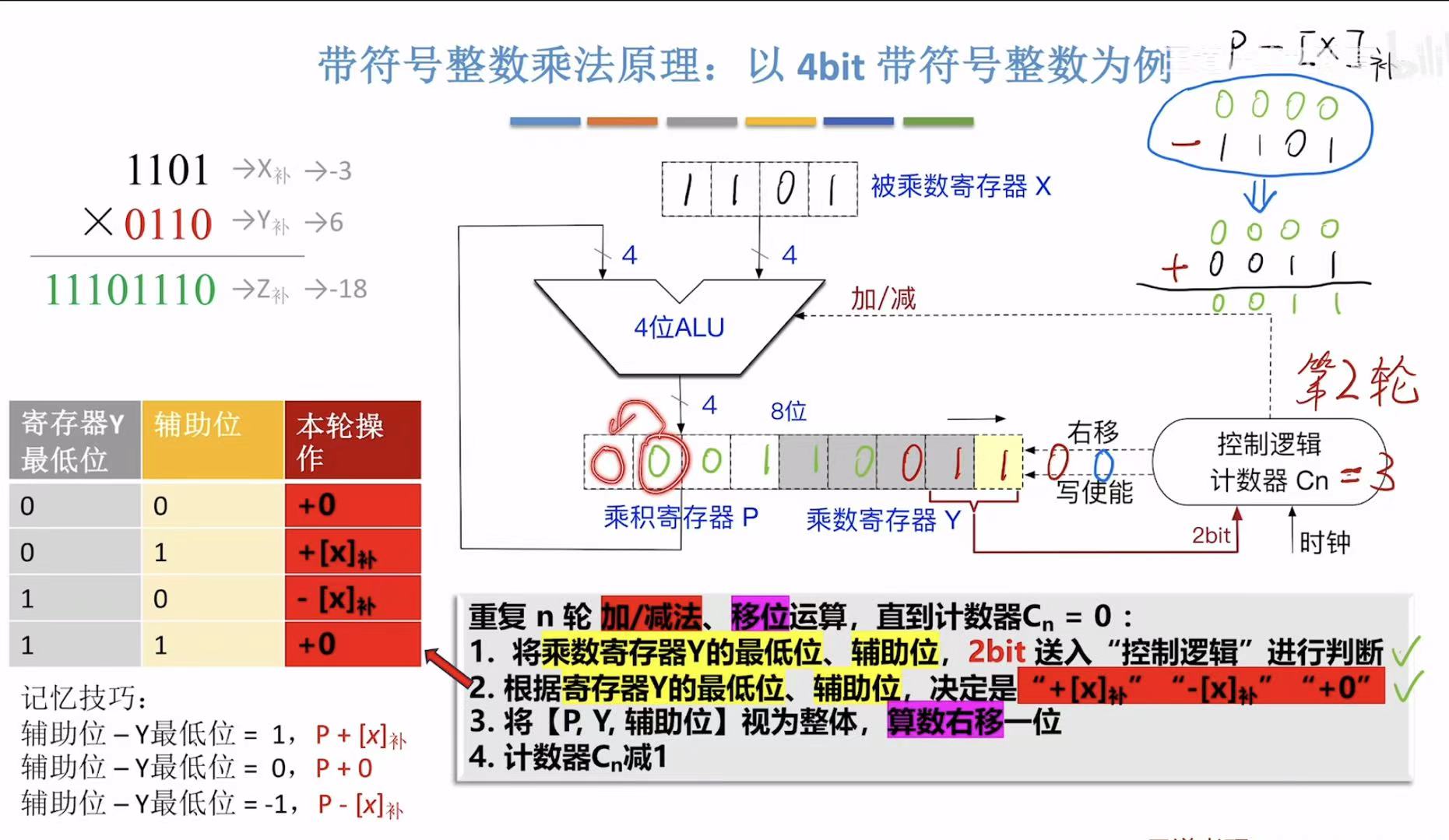
老规矩: - 01,就是进行+x[补]的执行
- 其余相同
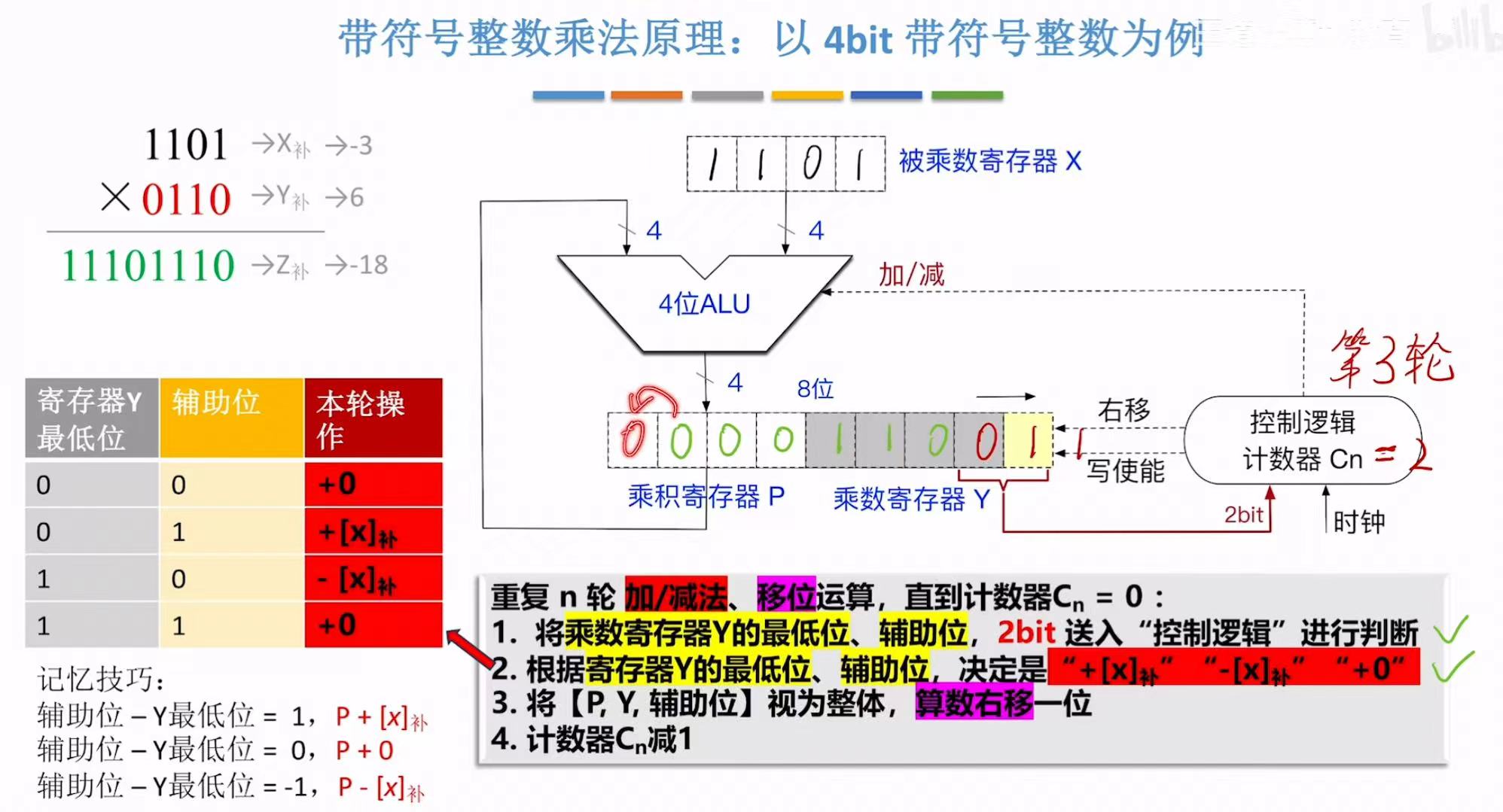
这里的补的空位因为空位后是1,所以补上的也是1。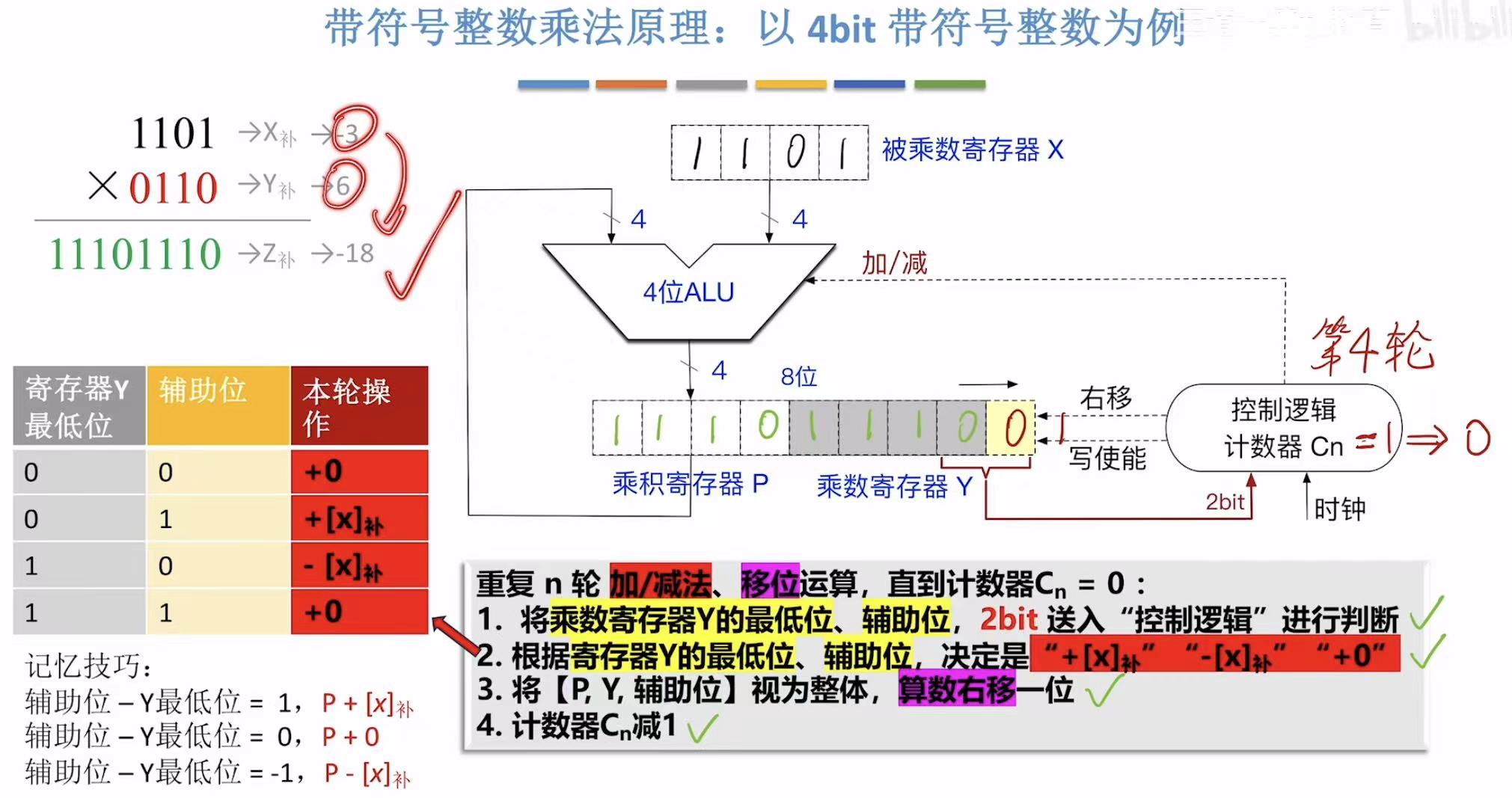
和无符号的一样,最后保留的都是后几位,故而肯定也会发生溢出现象。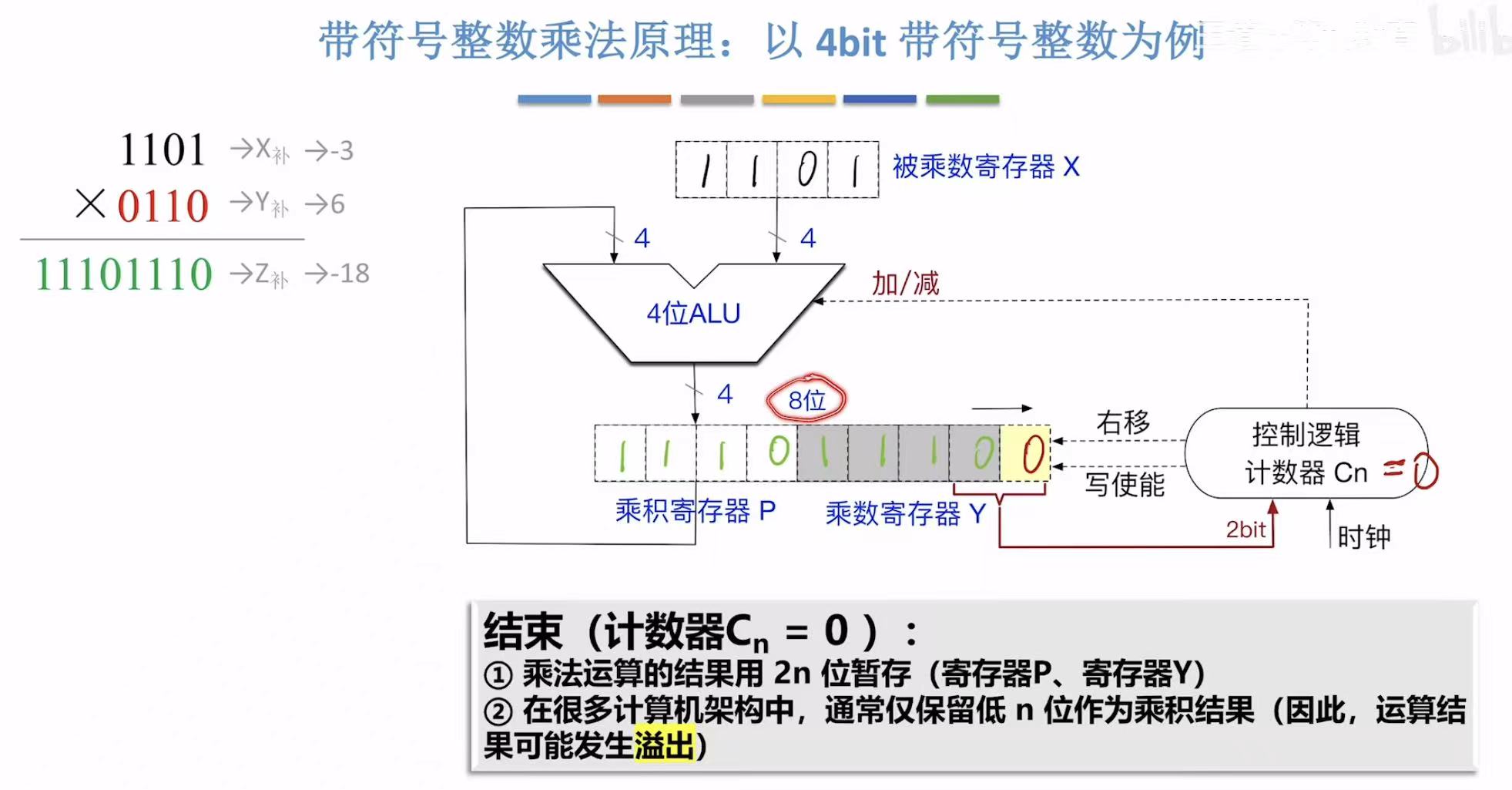
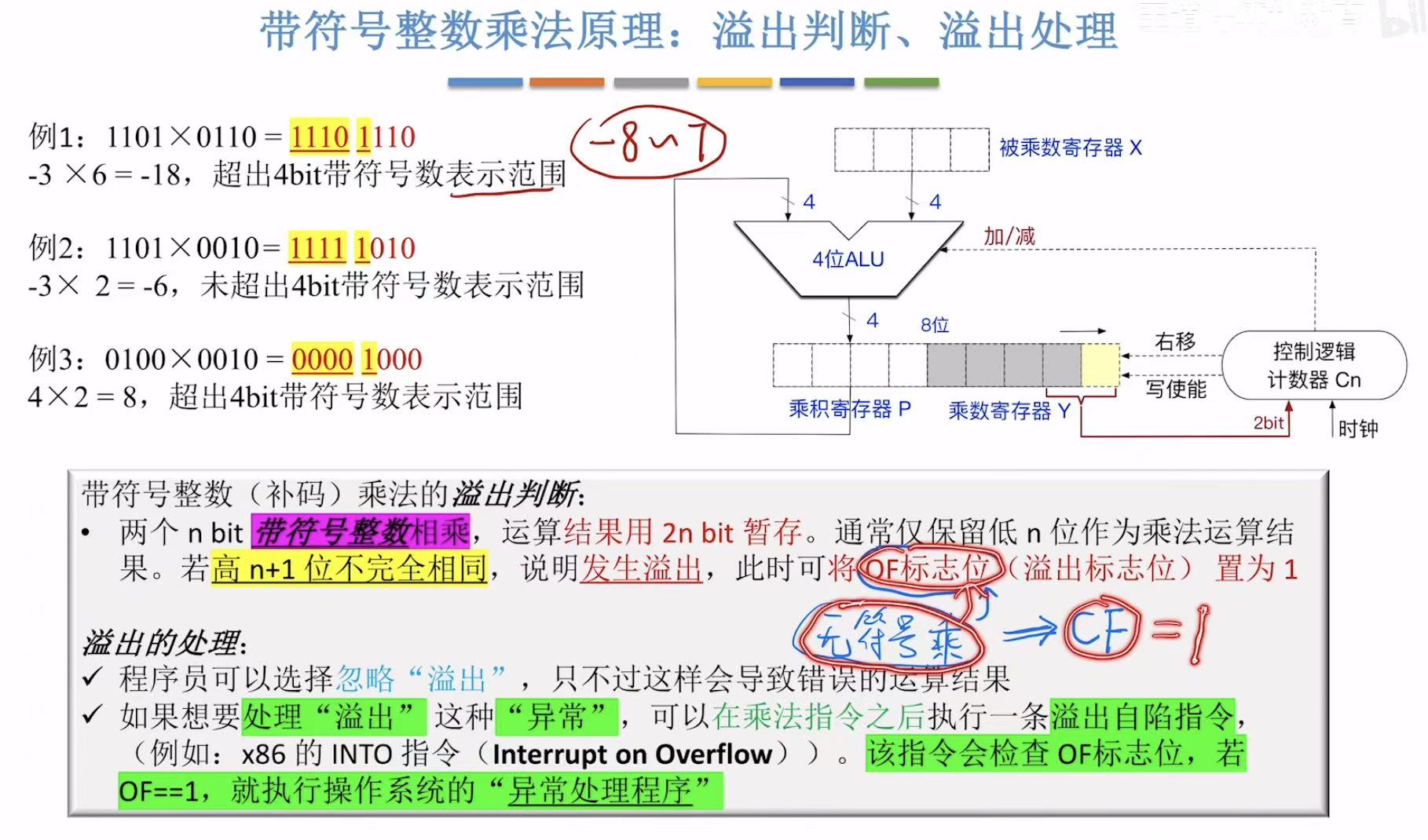
2.2 溢出判断及处理
补充:
- 有符号数溢出标志。就是CF是无符号数溢出标志,OF
- 通俗一点说就是,即使有符号数相加/相减导致了CF=1也没什么意义,不能说明结果的正确与否。
- 此时,OF=1, 则说明结果溢出,出现错误;OF=0,说明结果正确。 这个过程根本和CF没关系,CF=1/0,都不会影响。
- 同理也 许可得出OF对无符号数也无影响。 大家可能已经发现了,通过公式将减法转换成加法,貌似不完全等价,因为CF不同。
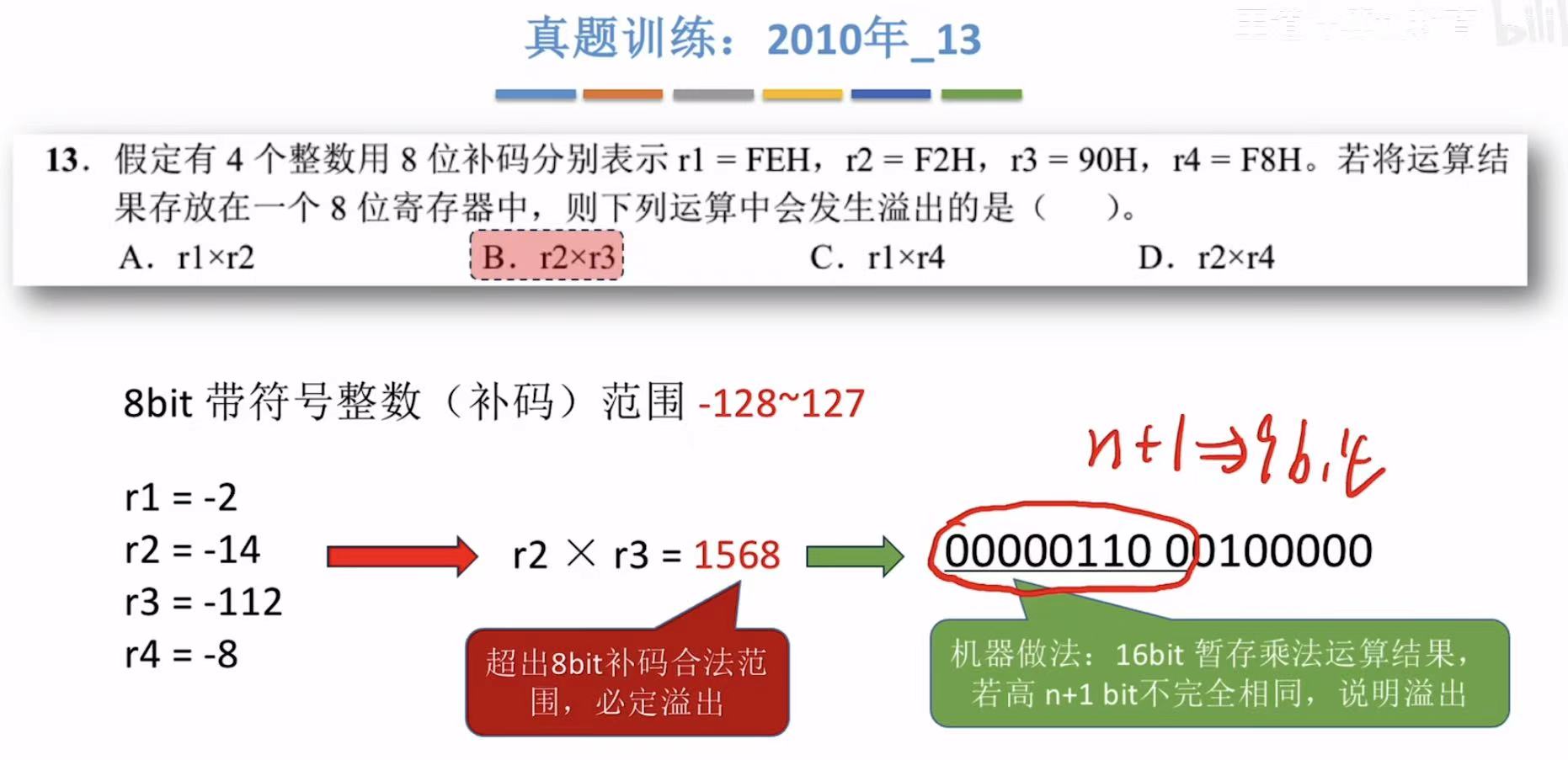
真题训练:
3. 32位乘法运算电路
位数变多了而已。就是和四位的过程一模一样,就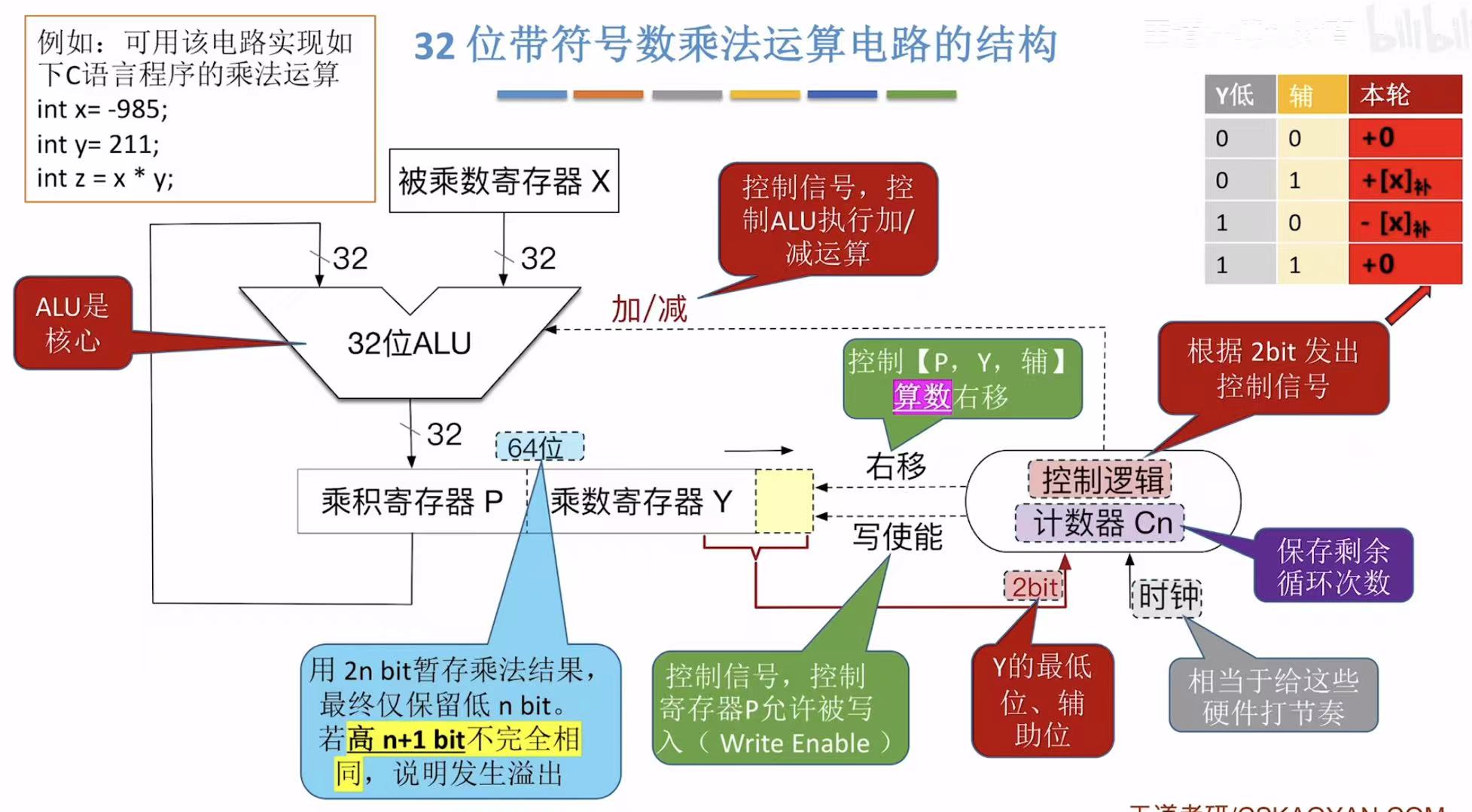
4. 小结
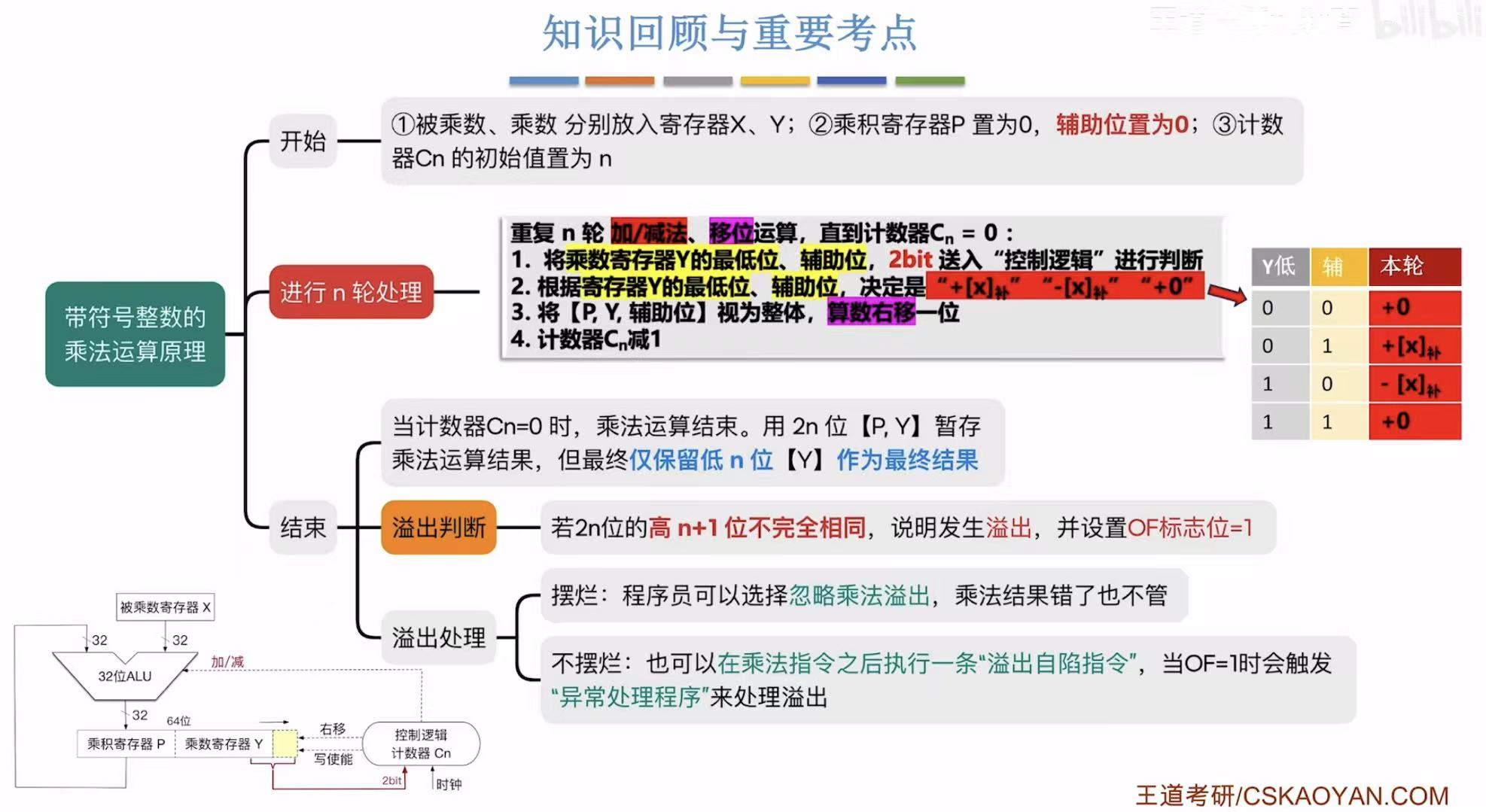
5. 补充-布斯乘法

计算机达成乘法运算的三种方式
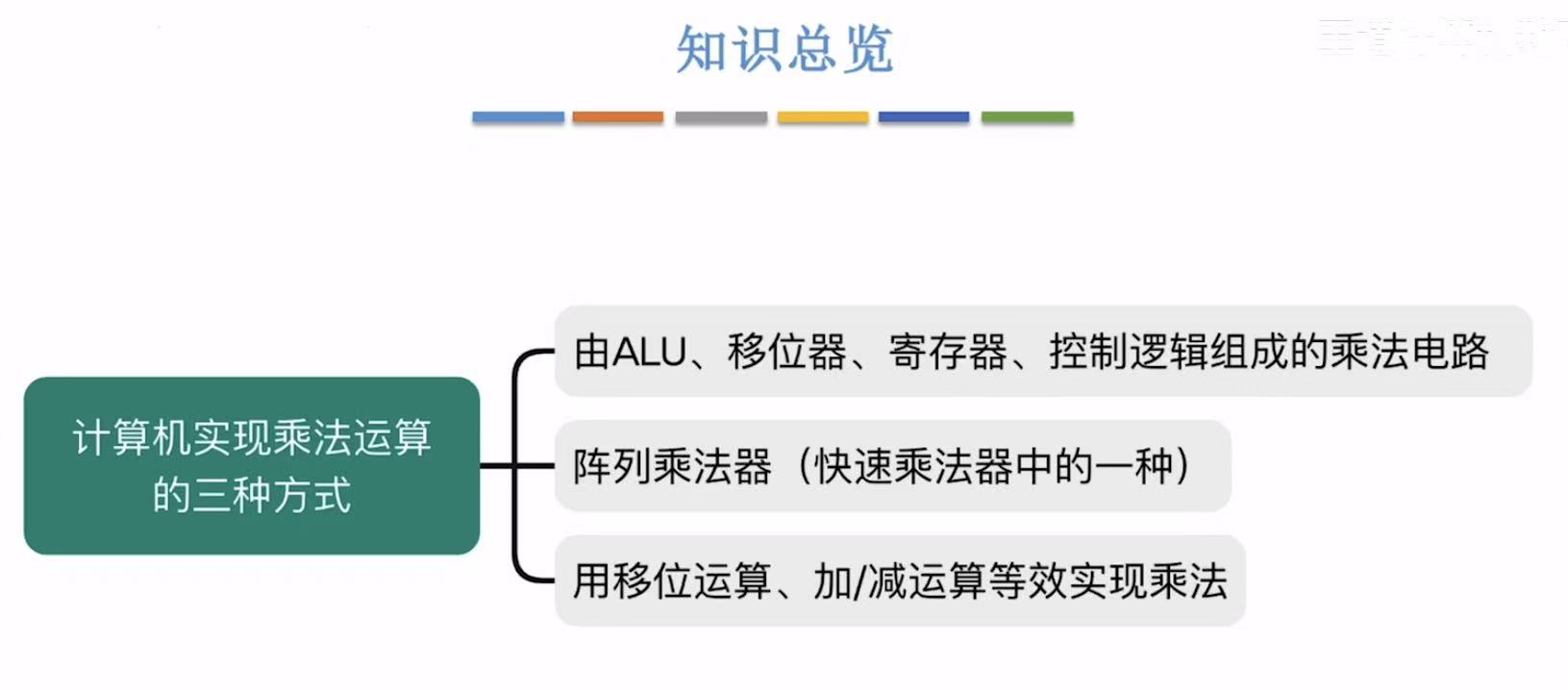
1. ALU
就是大家上文用到的东西。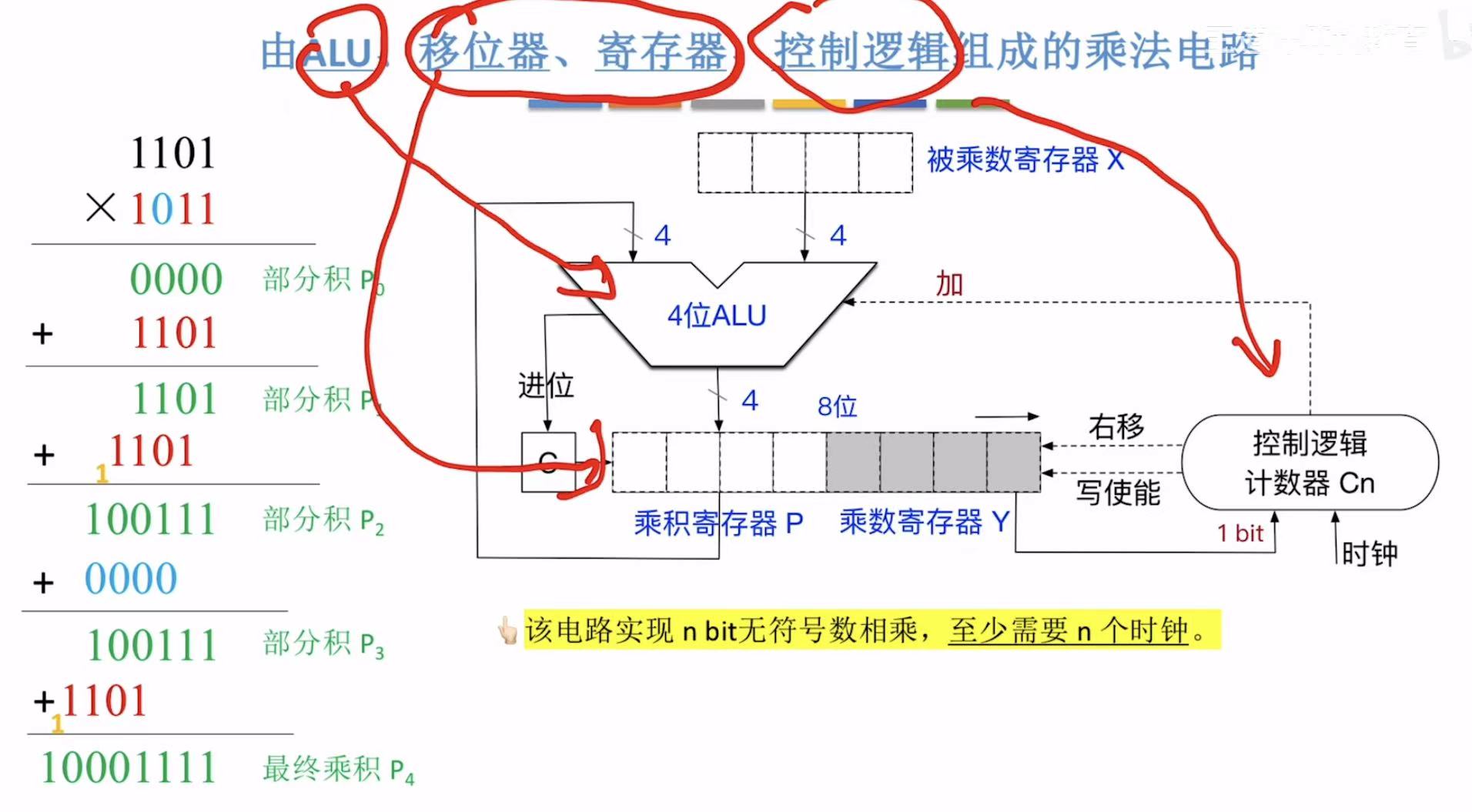
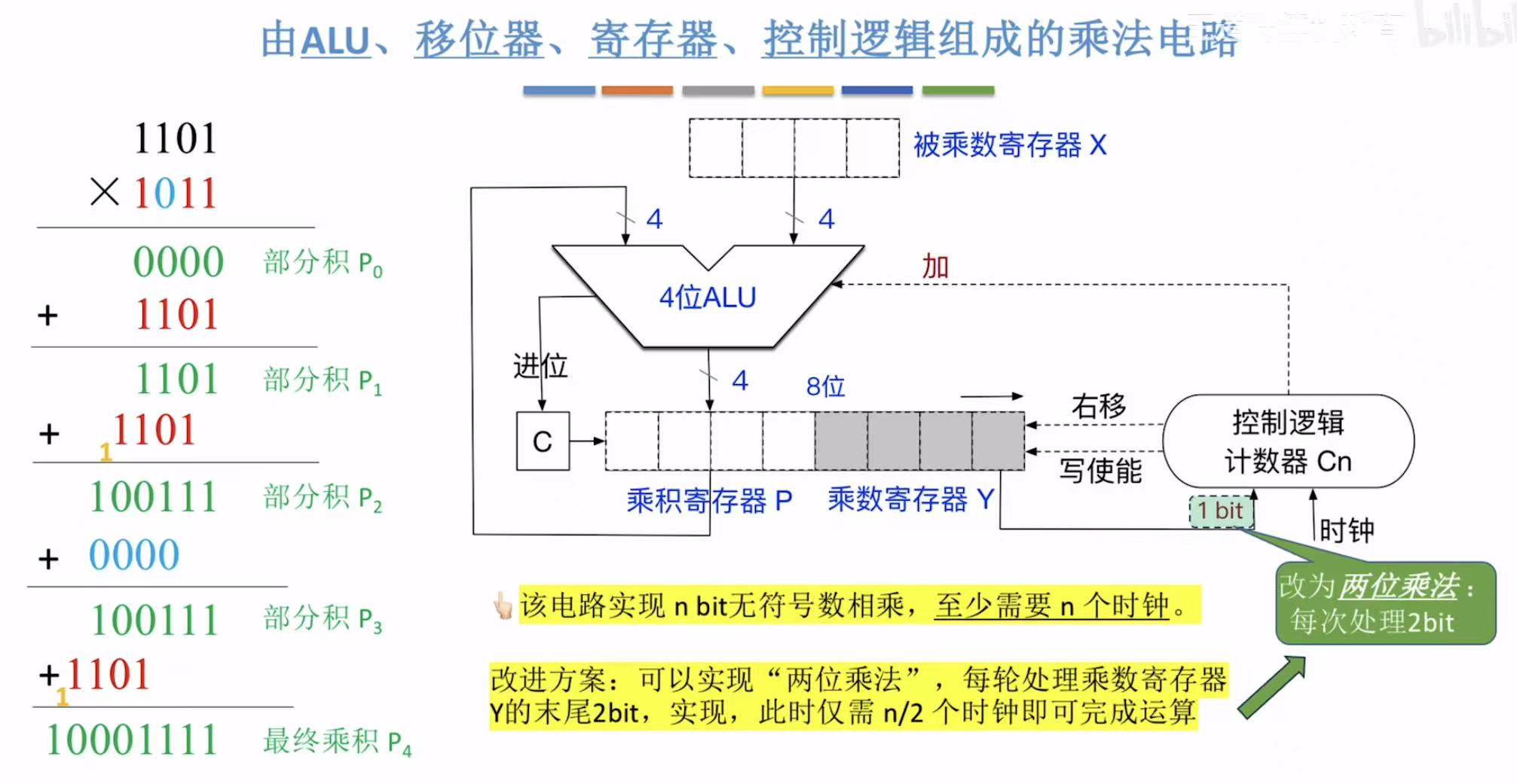
2. 阵列乘法器
快速乘法器!!!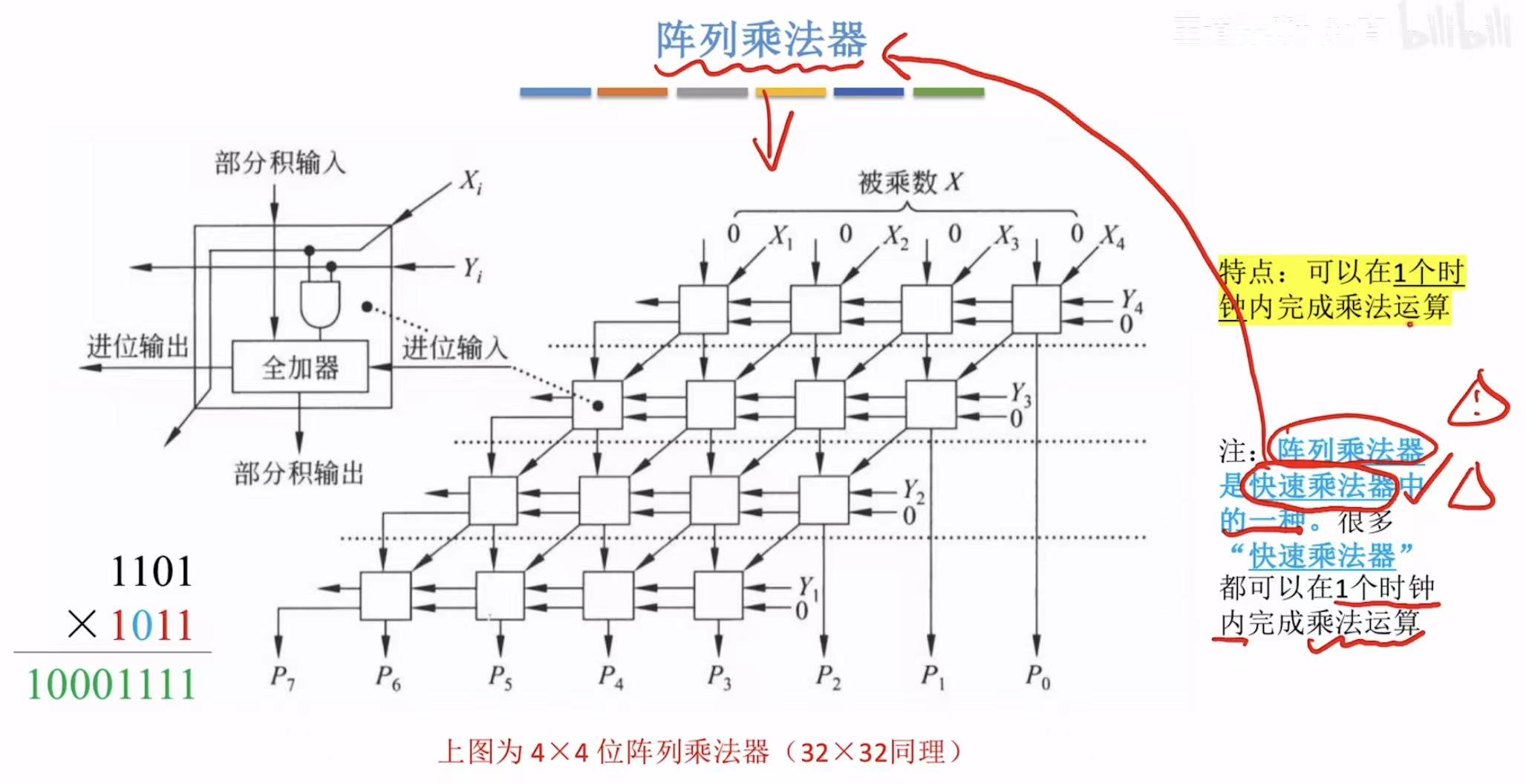
3. 逻辑运算
最慢的一种了
真题训练:
4. 对比
按速度快慢:阵列>ALU>逻辑运算
5. 小结
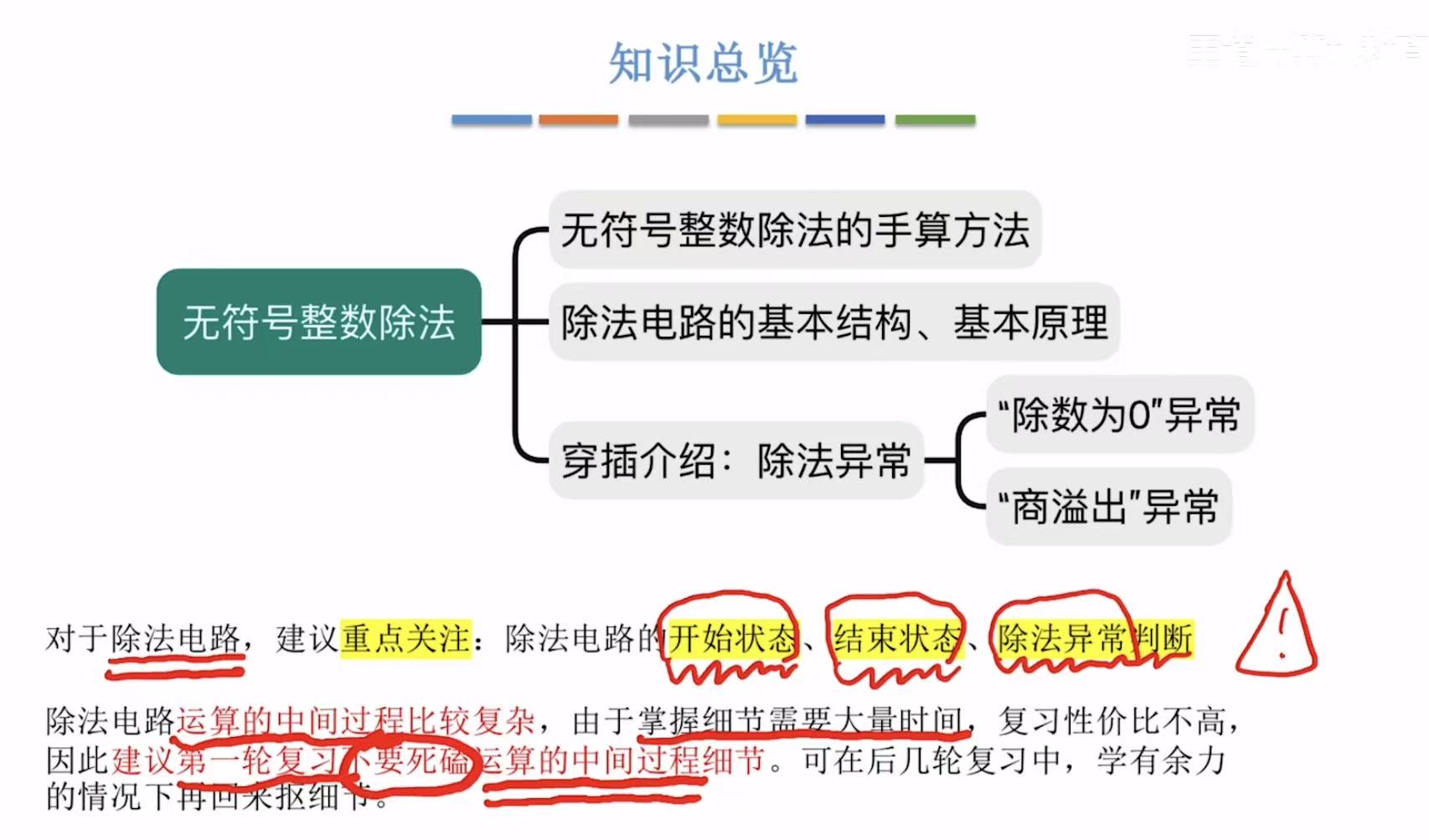
无符号整数除法
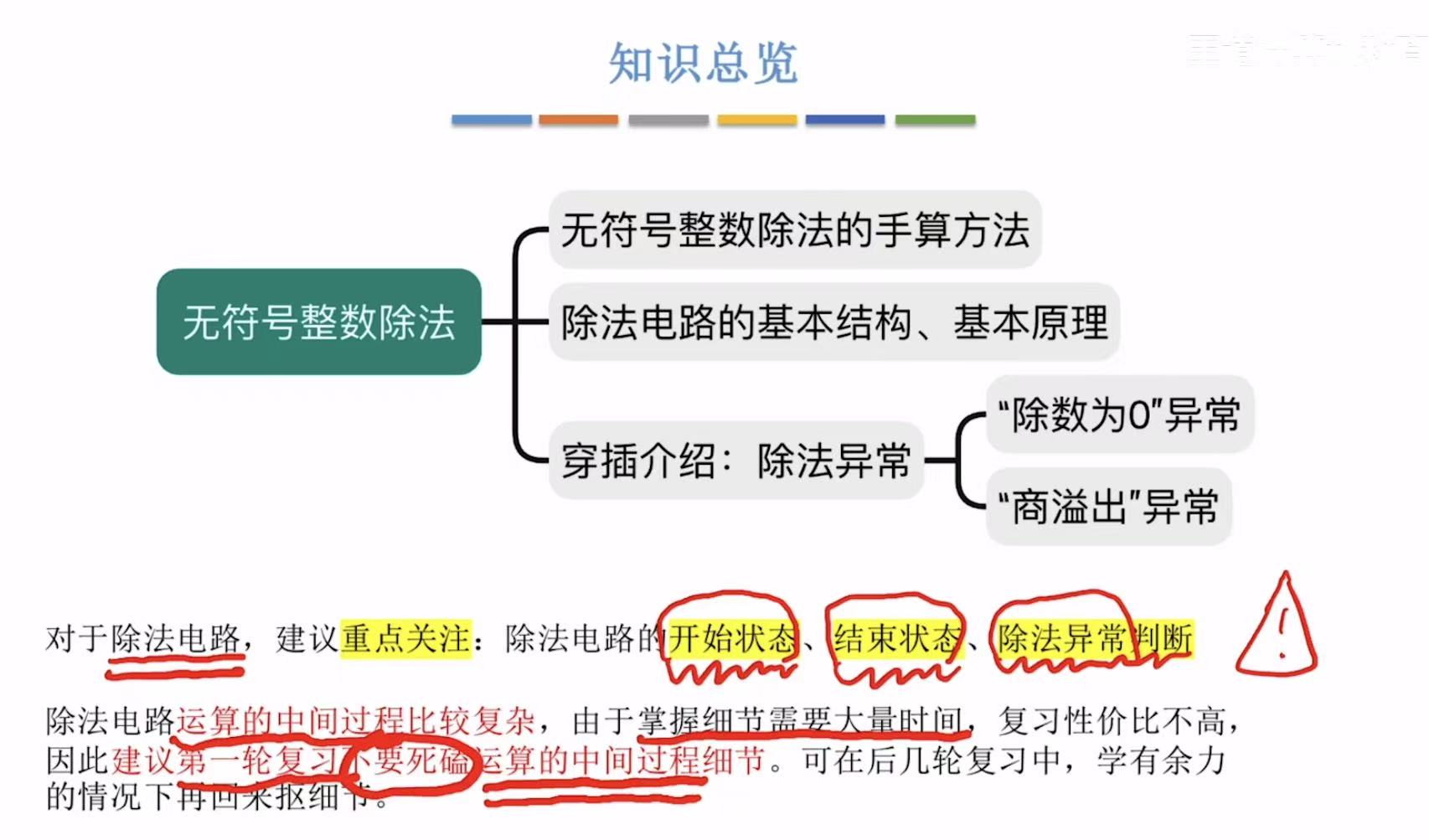
1. 手算除法
引入余数的概念。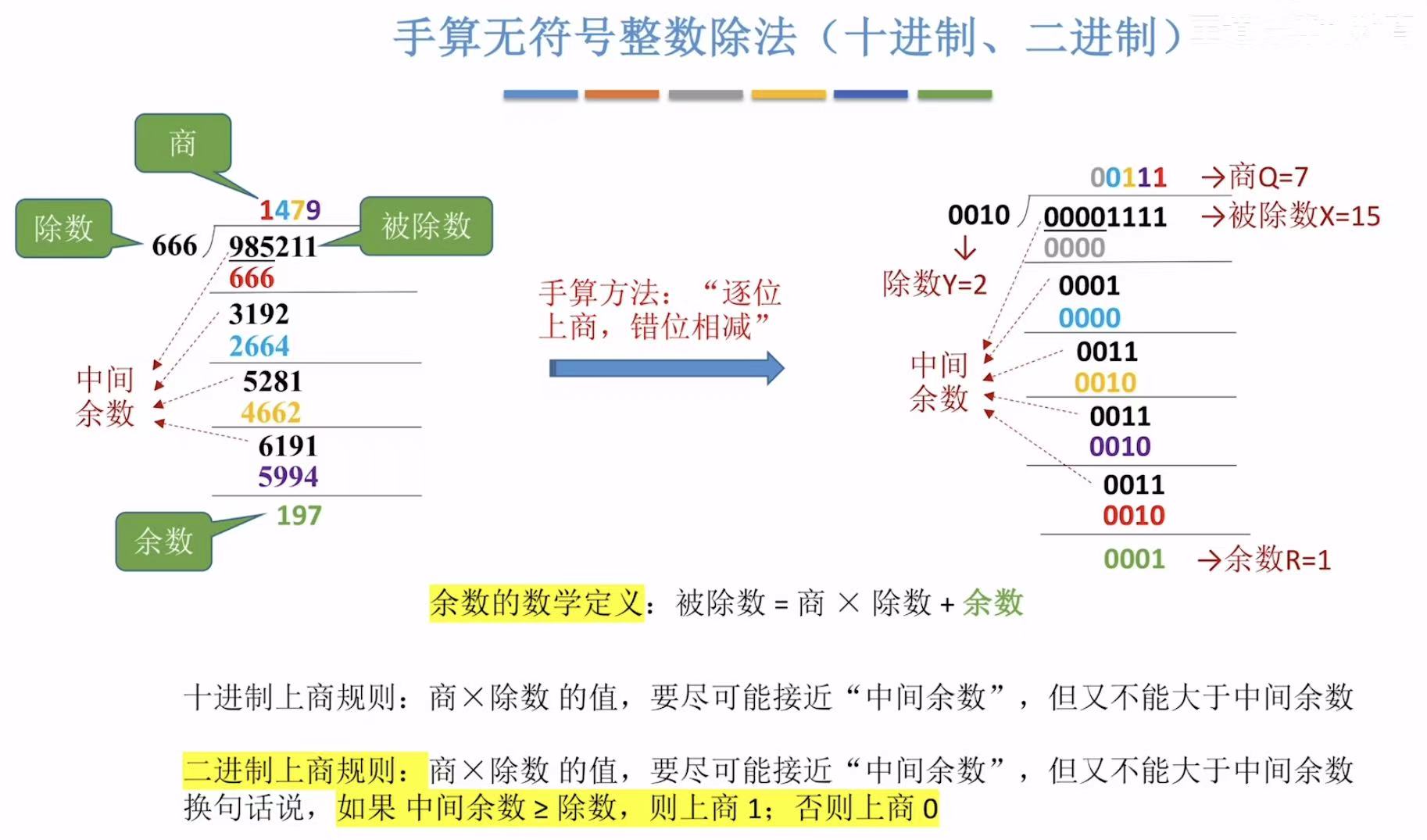
2. 除法原理
第一步都是先各就各位。
零拓展:被除数不够2n位,就添0,让他达到2n位。
注意特殊情况:除数为0or被除数<除数。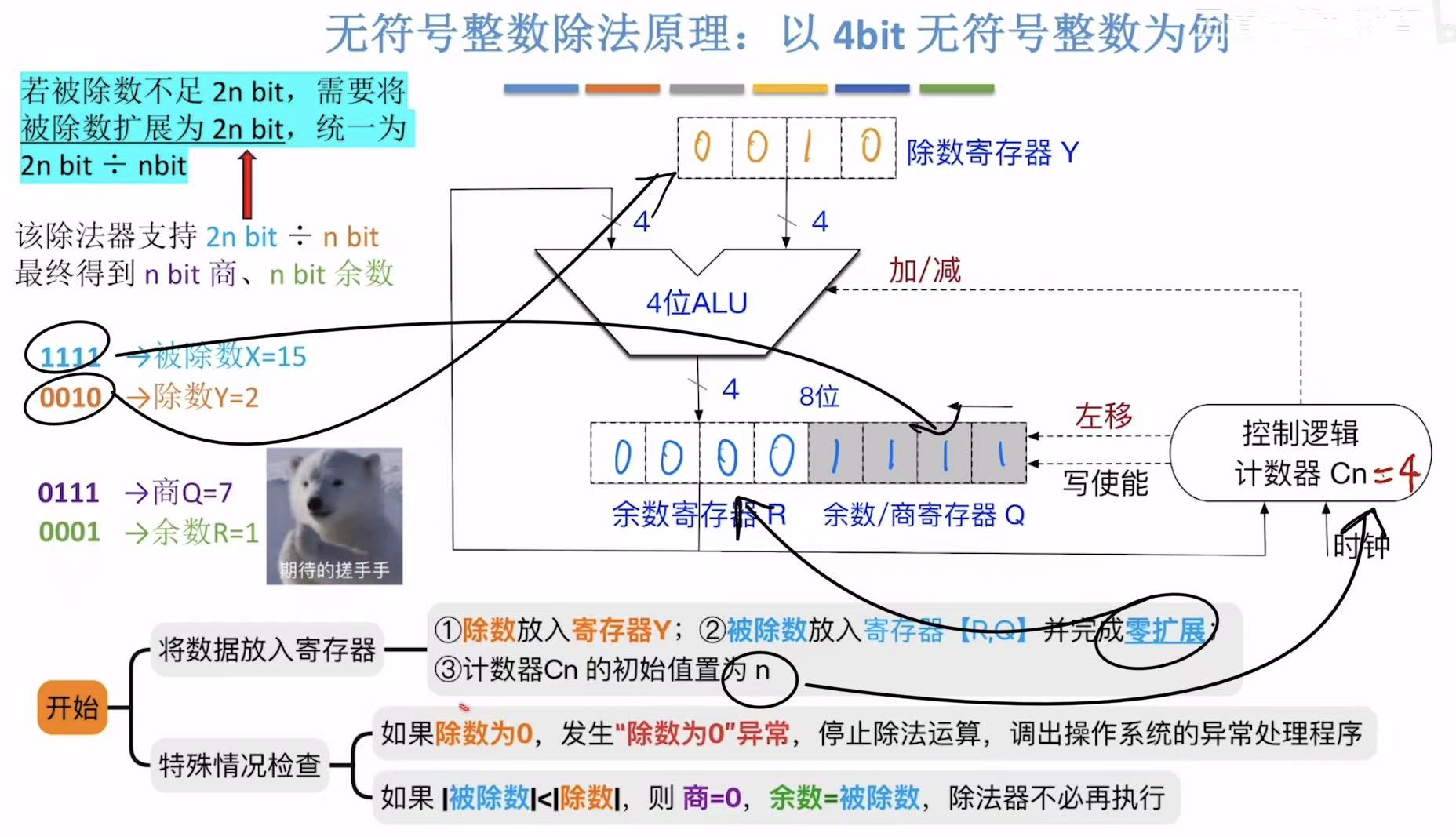
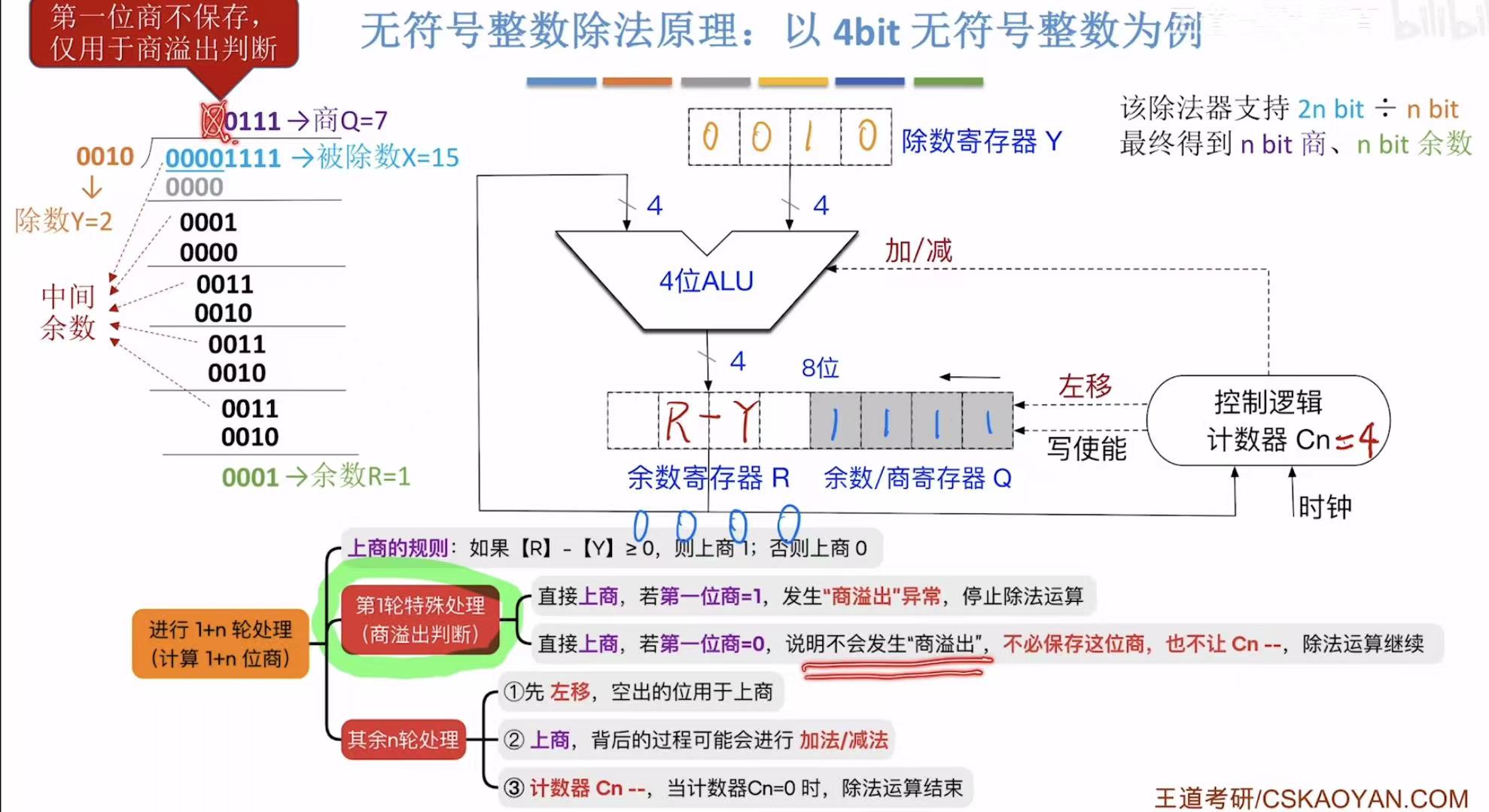
3. 32位除法运算电路
位数变多了而已。就是和四位的过程相同,就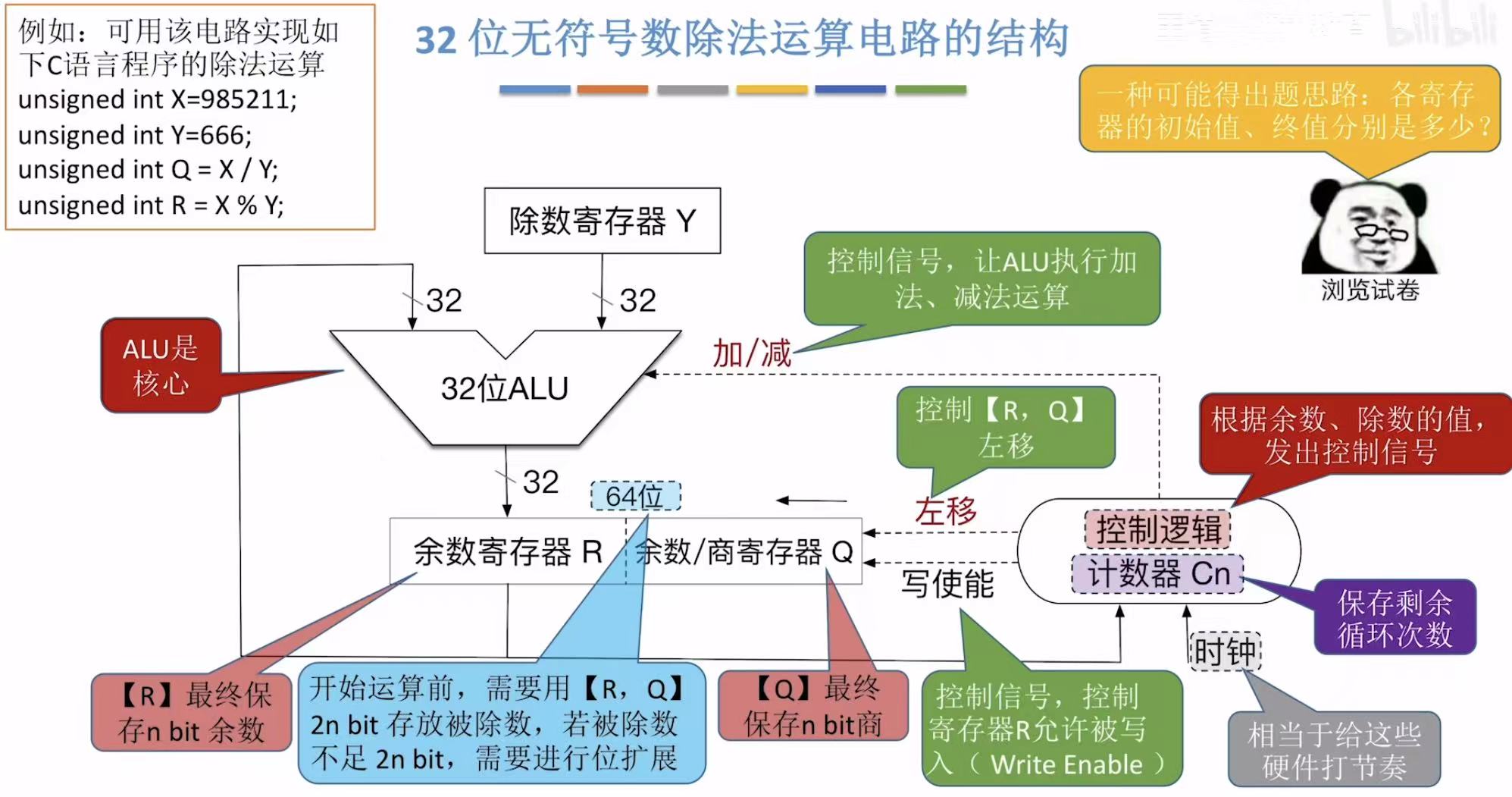
4. 商溢出
只有位数多/位数少的时候才可能发生商溢出。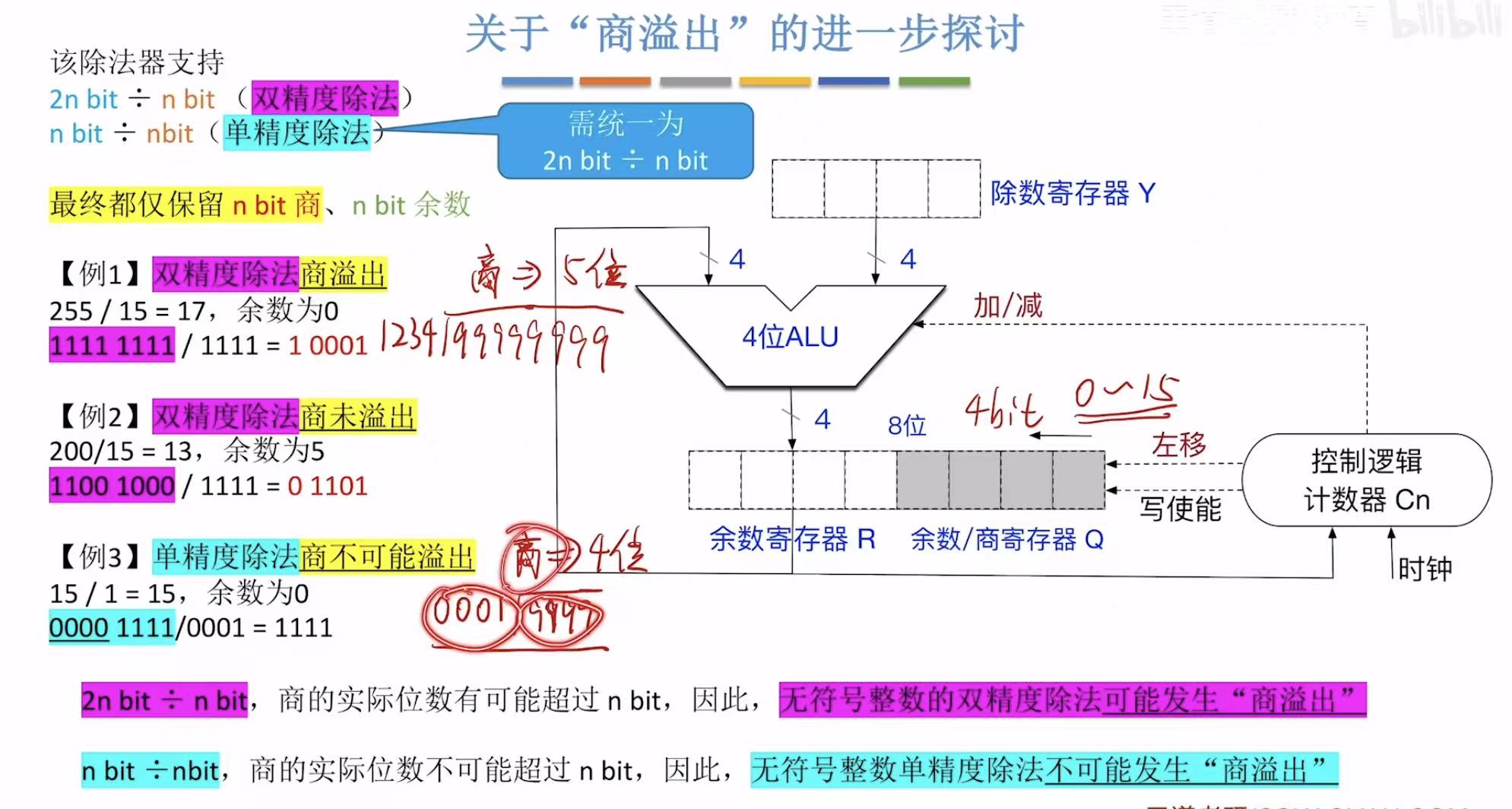
5. 小结
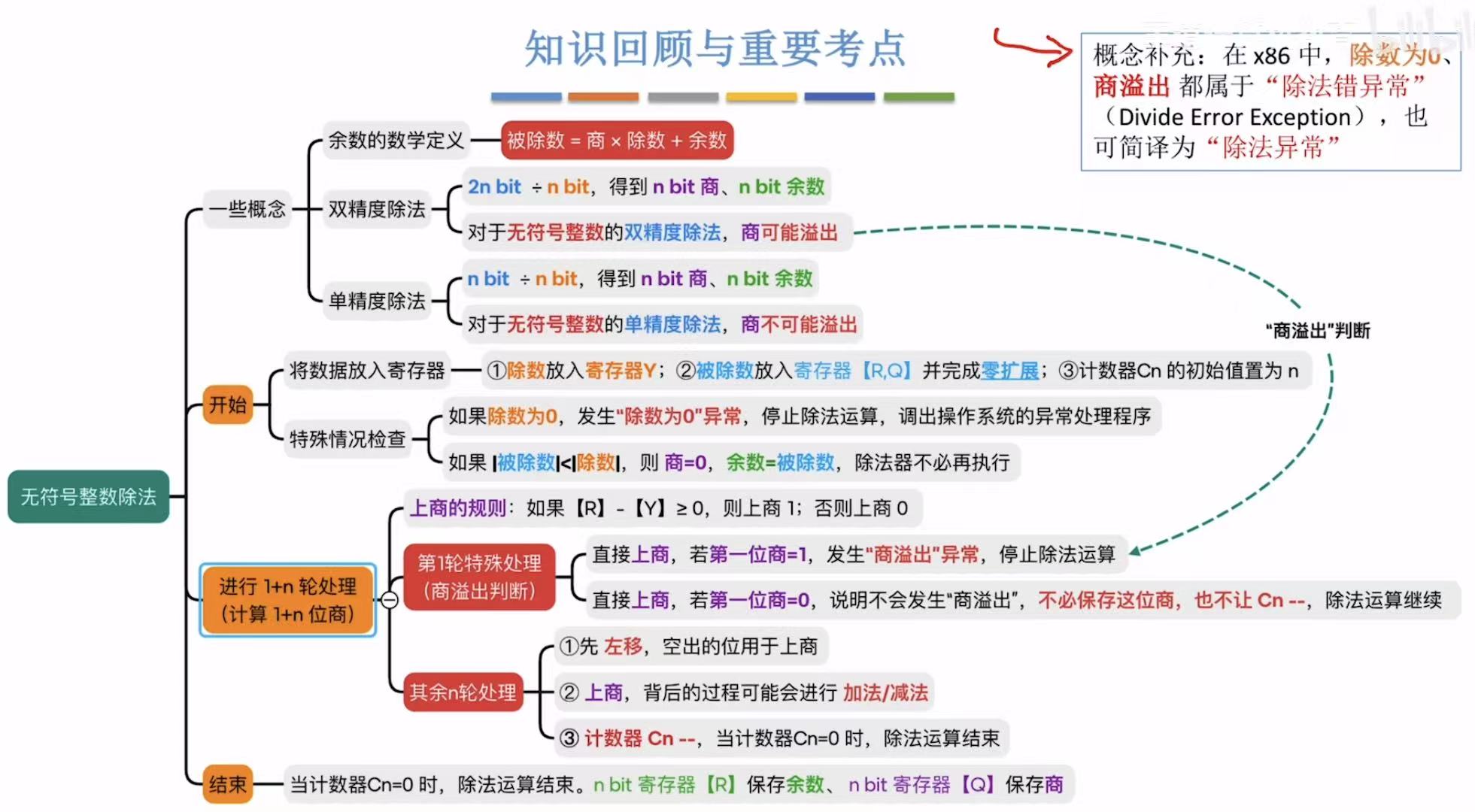
IEEE浮点数的表示
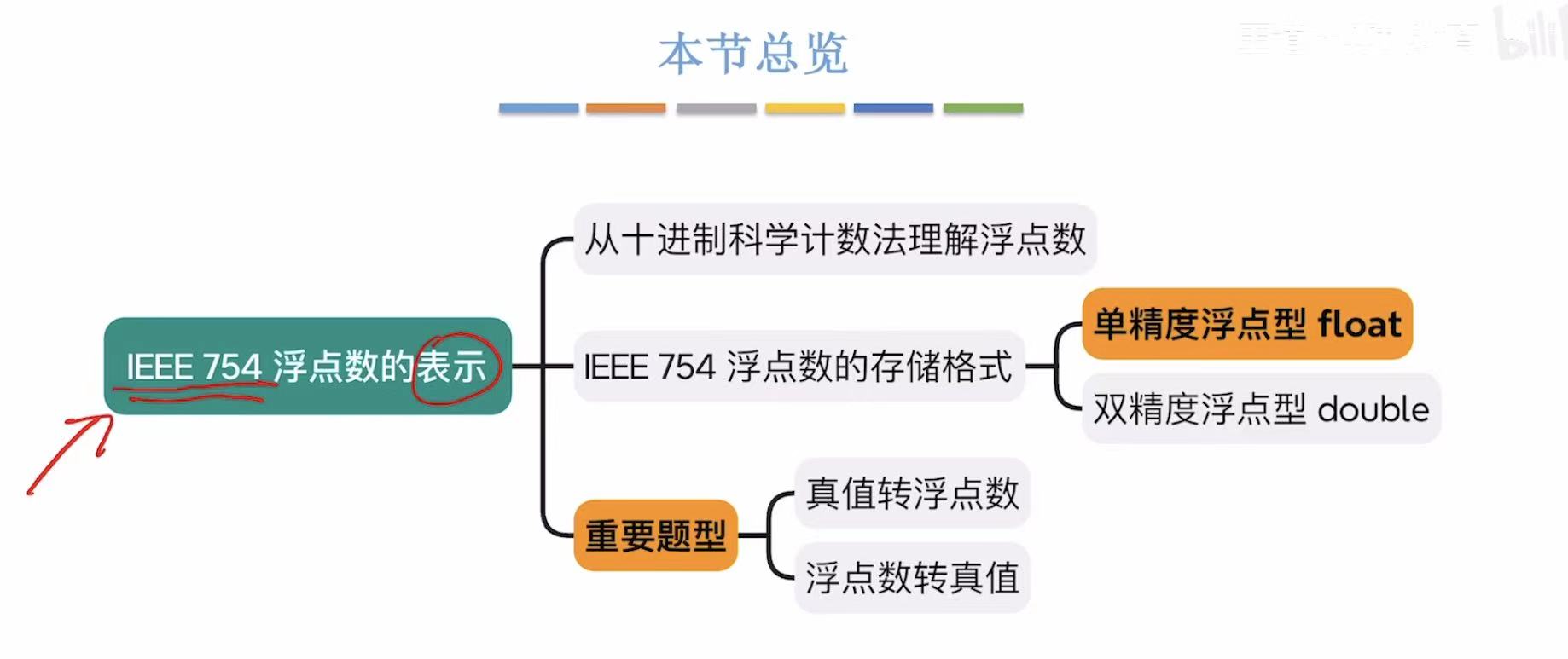
1. 从科学计数法理解浮点数
如果用一个定点数表示超极长的数字,就不好识别,于是出现了科学计数法。
统一为:符号 一位数字 小数点 ×10的n次幂
整数部分只有一个非零数字。就是规格化就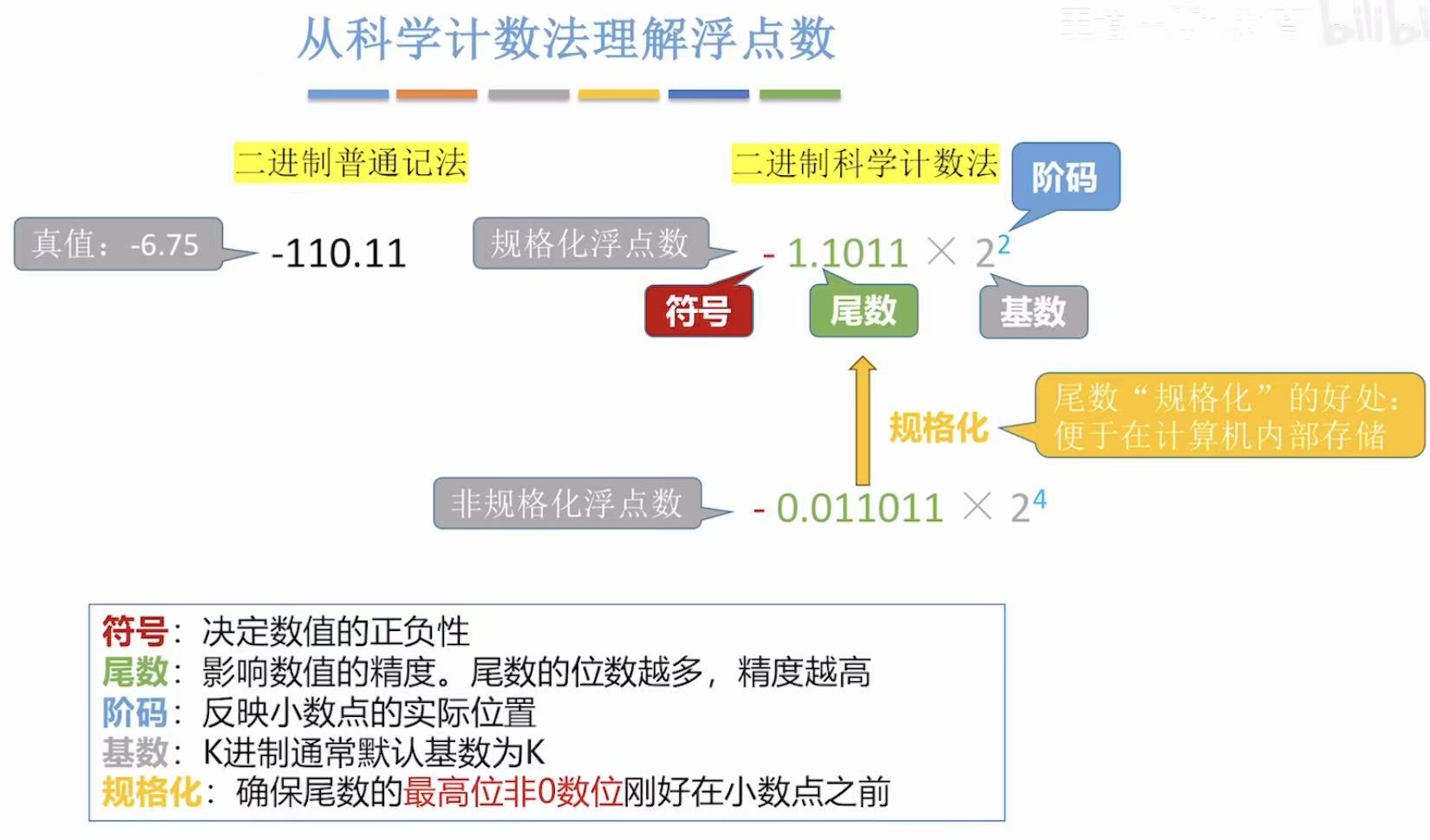
2. IEEE754标准定义的浮点数格式
类比十进制,二进制的科学计数法也是这个样子的。(二进制科学计数法纯是为了方便理解,不是术语)
把符号、尾数、阶码、基数都对应过来,就是图中长条方格的样子,记住这个就方便做题了。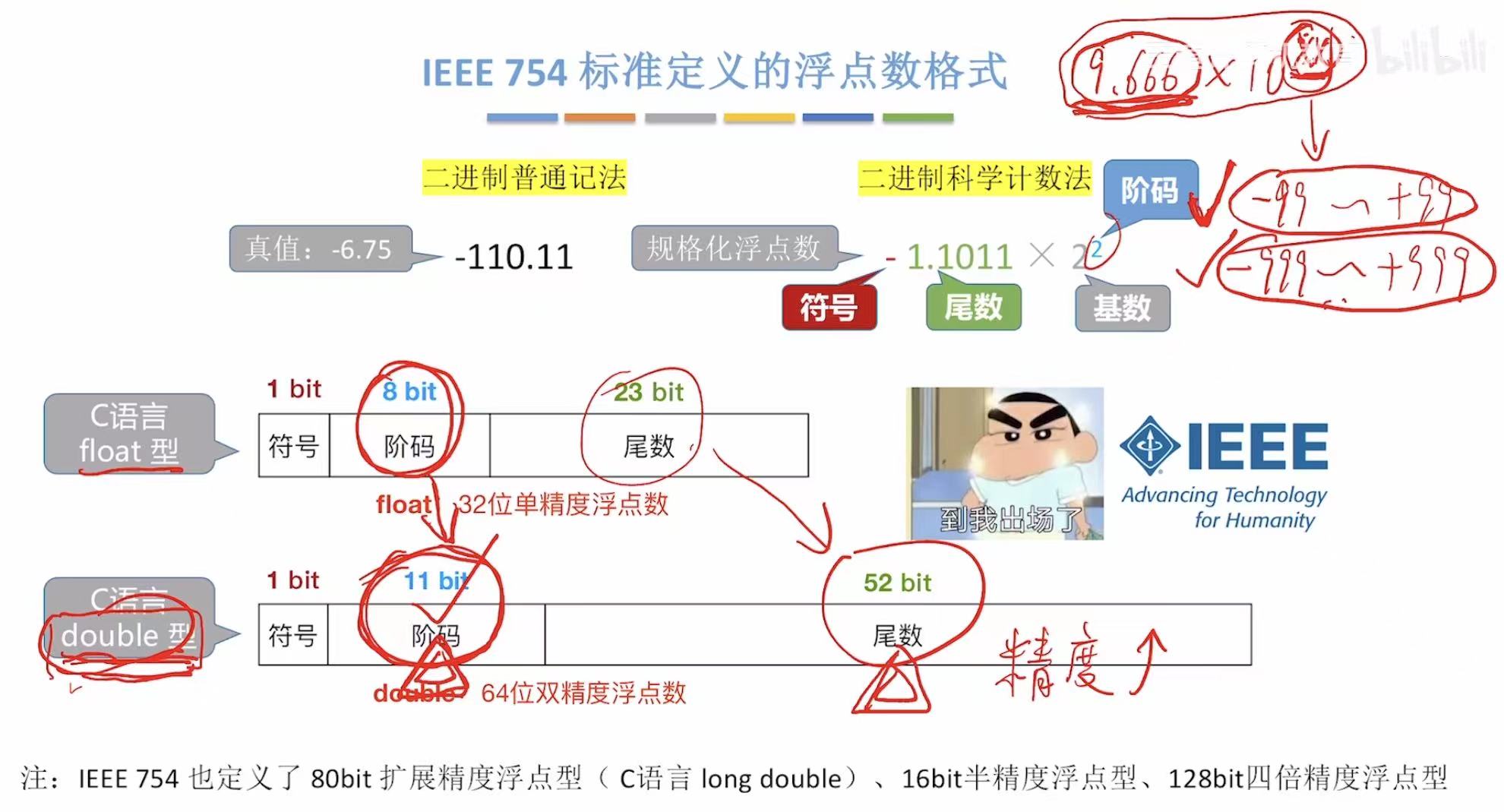
2.1 单精度
单精度:32位。
阶码:偏移值127+阶码本身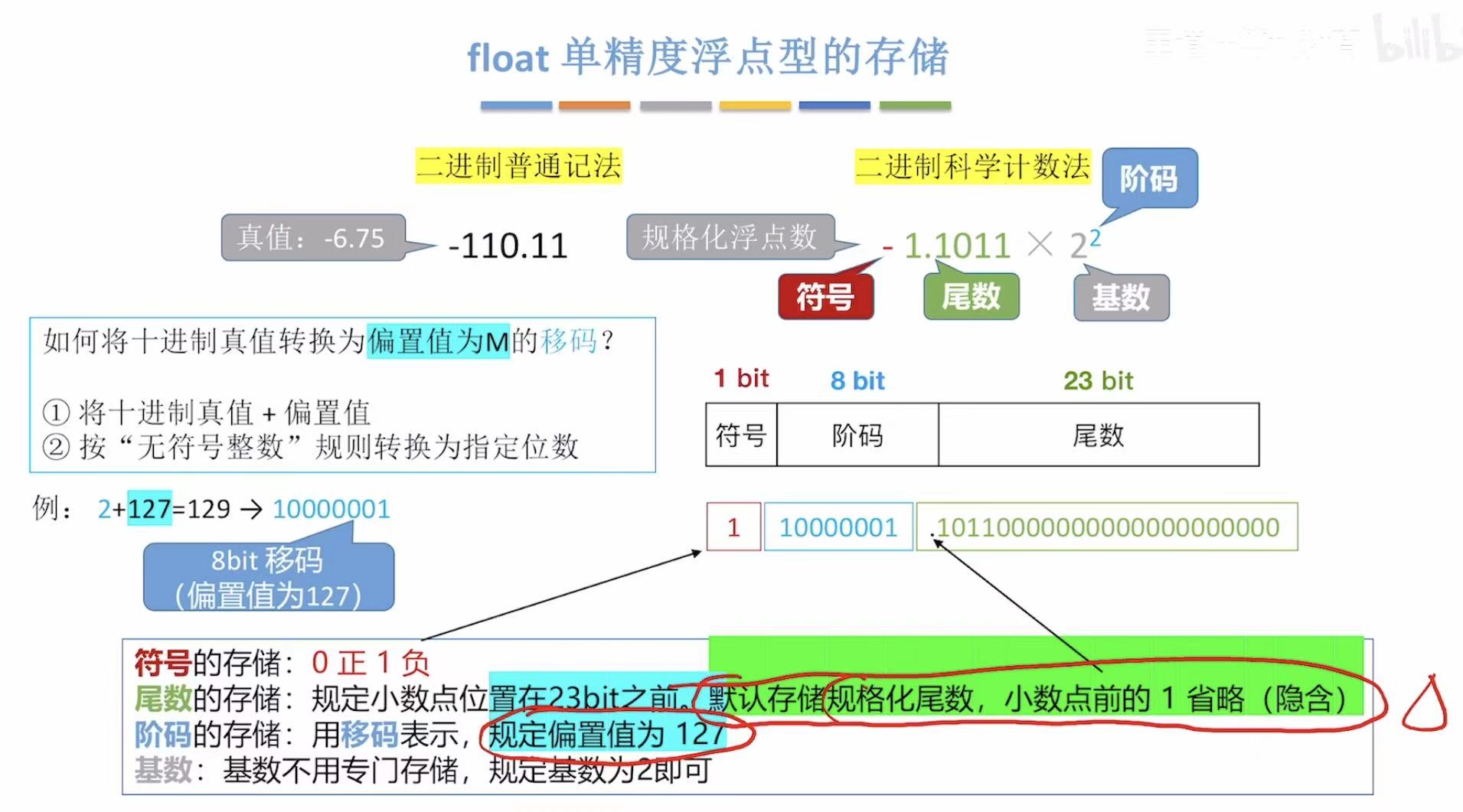
2.2 双精度
双精度:64位。(不够位数就用0补)
阶码:偏移值1023+阶码
3. 例题

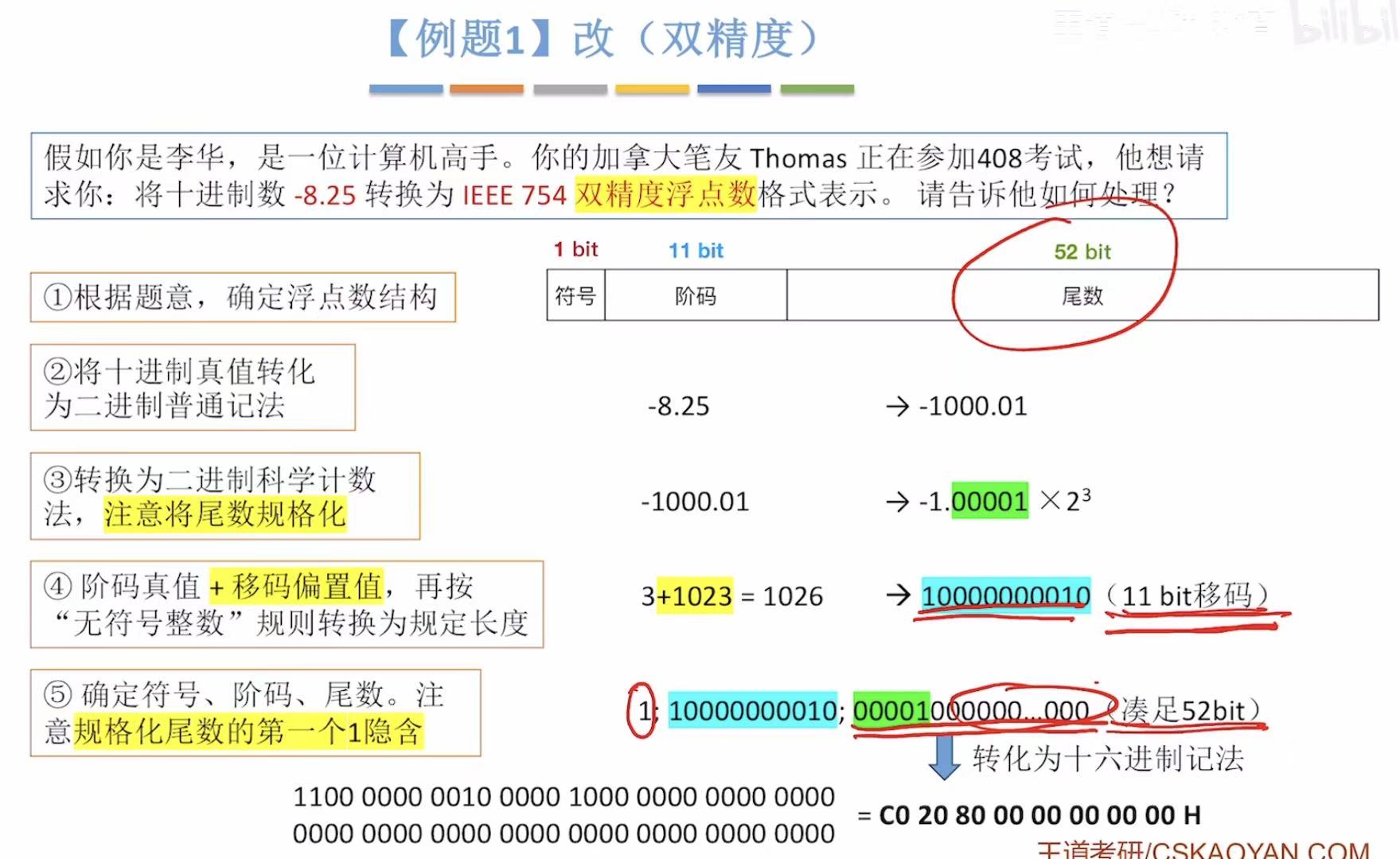
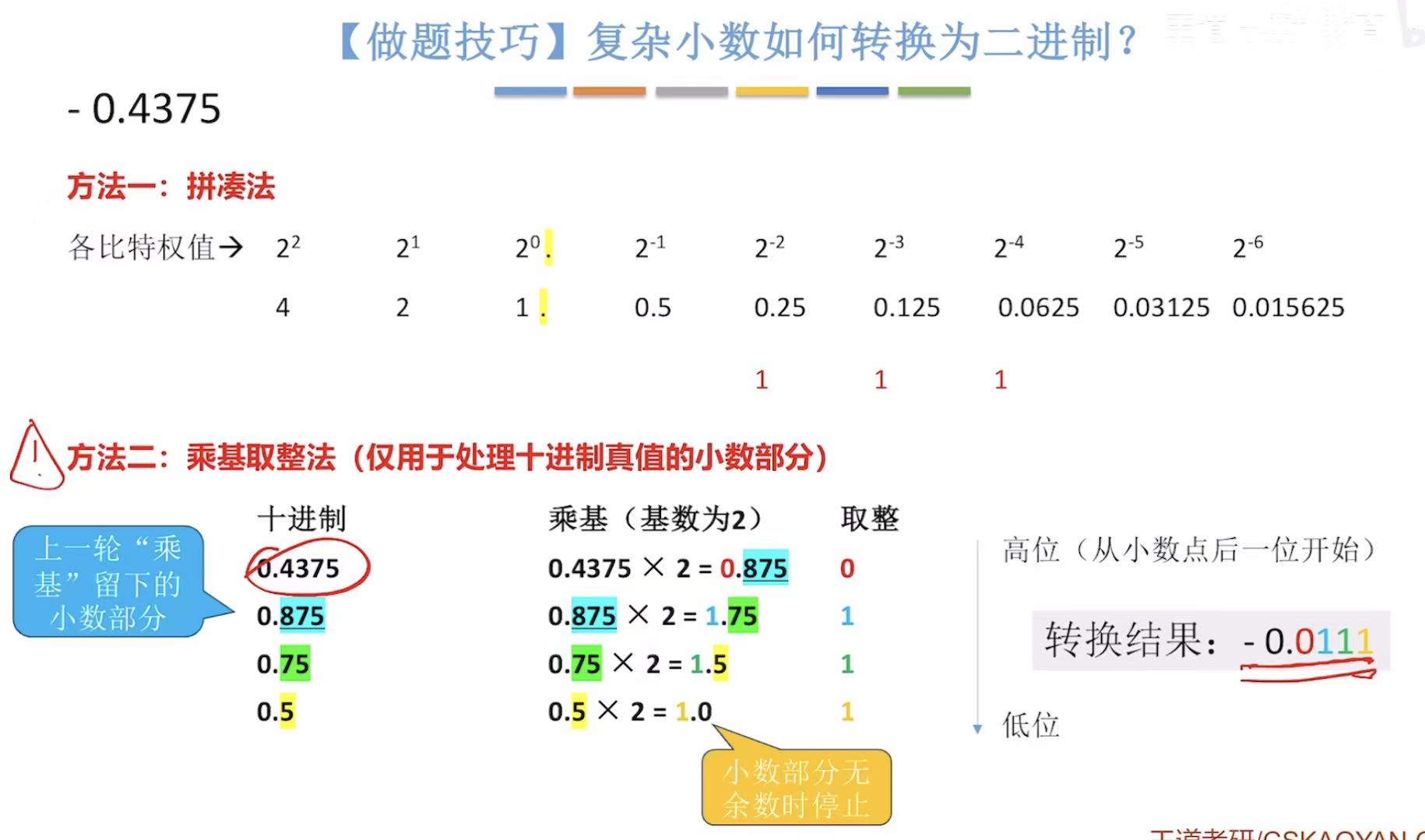
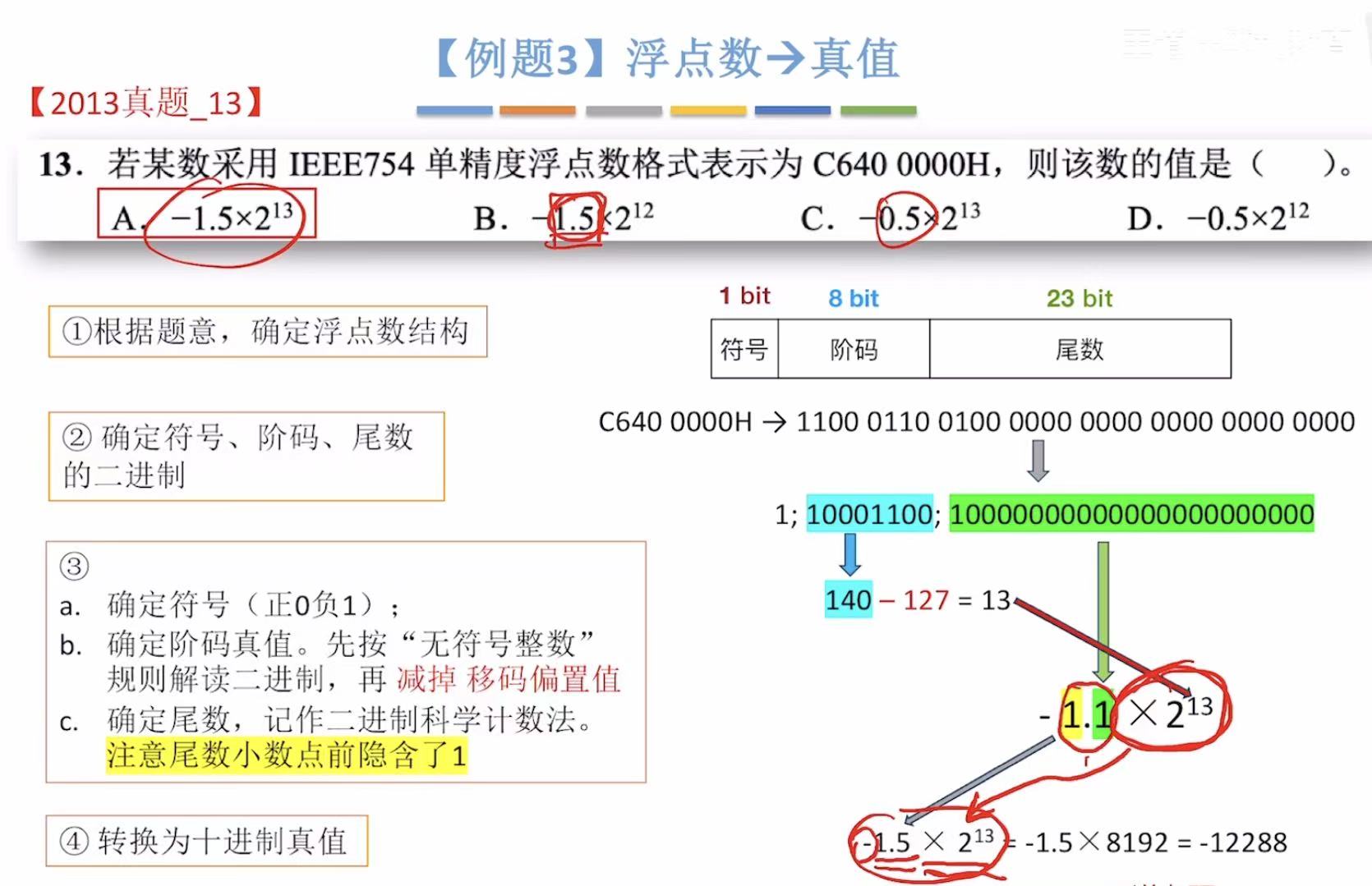
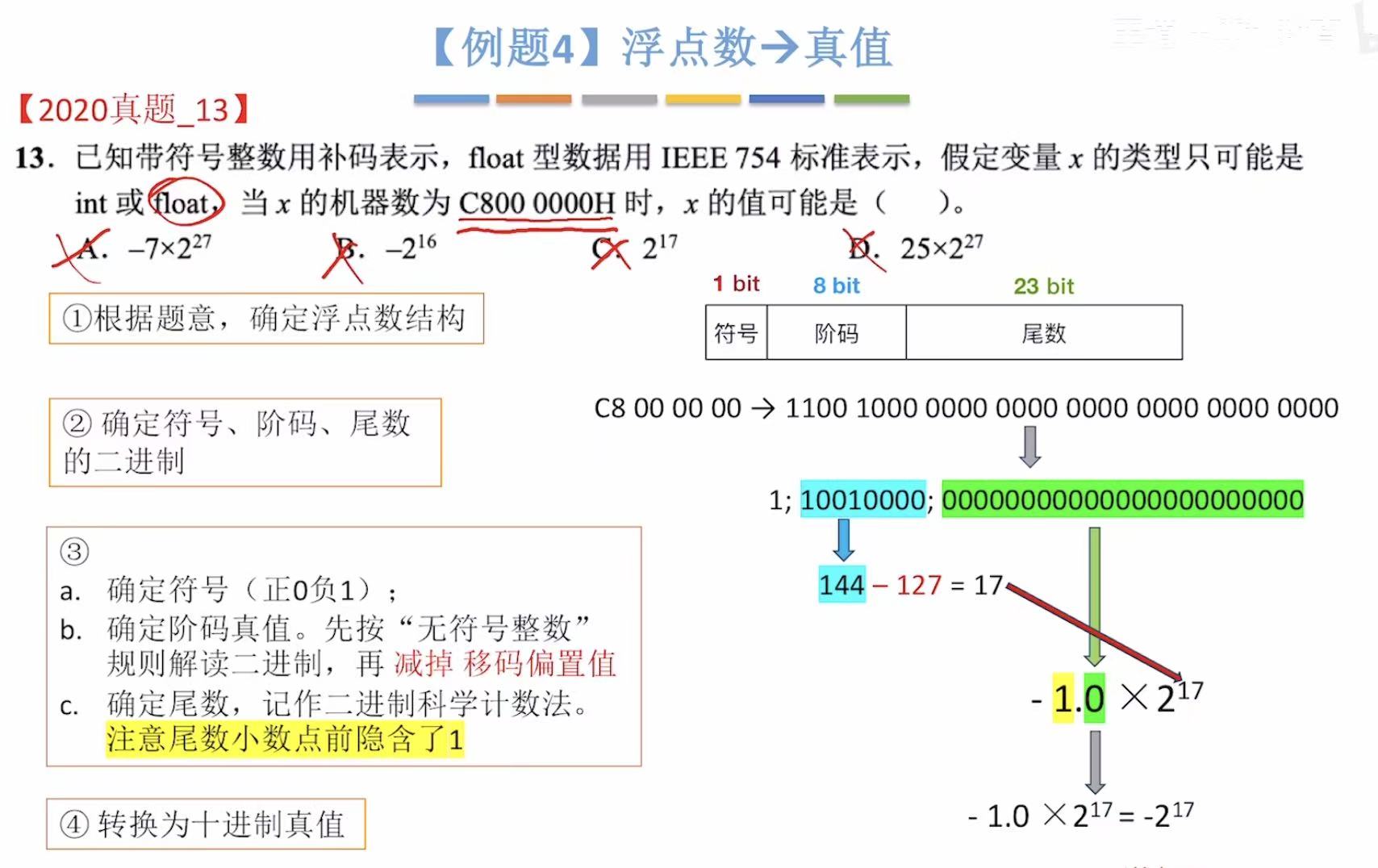

4. 小结
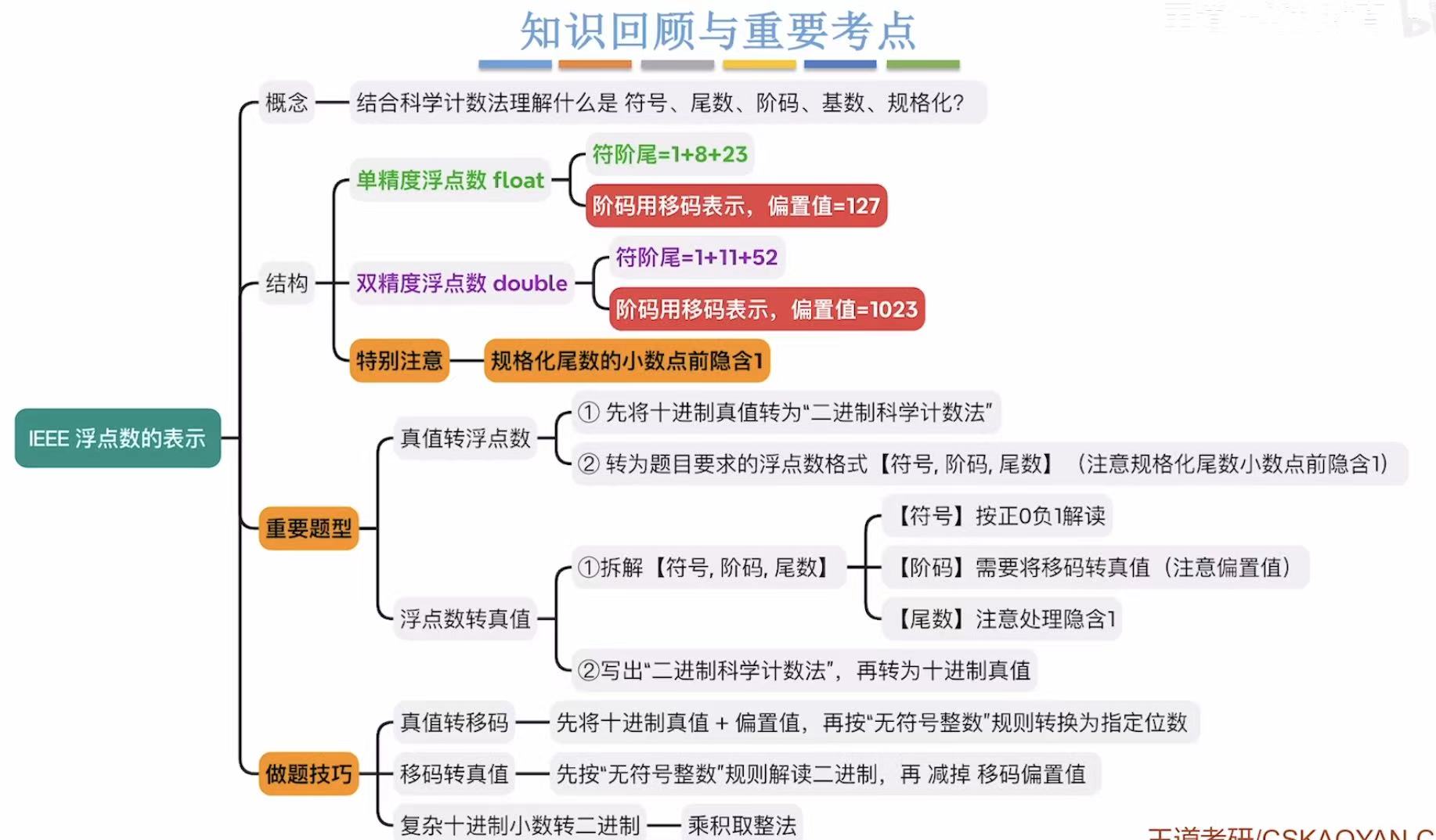
IEEE754浮点数的表示范围
1. 分类
就是浮点数中,阶码全为0或者全为1的时候,这个浮点数表示的什么意思。
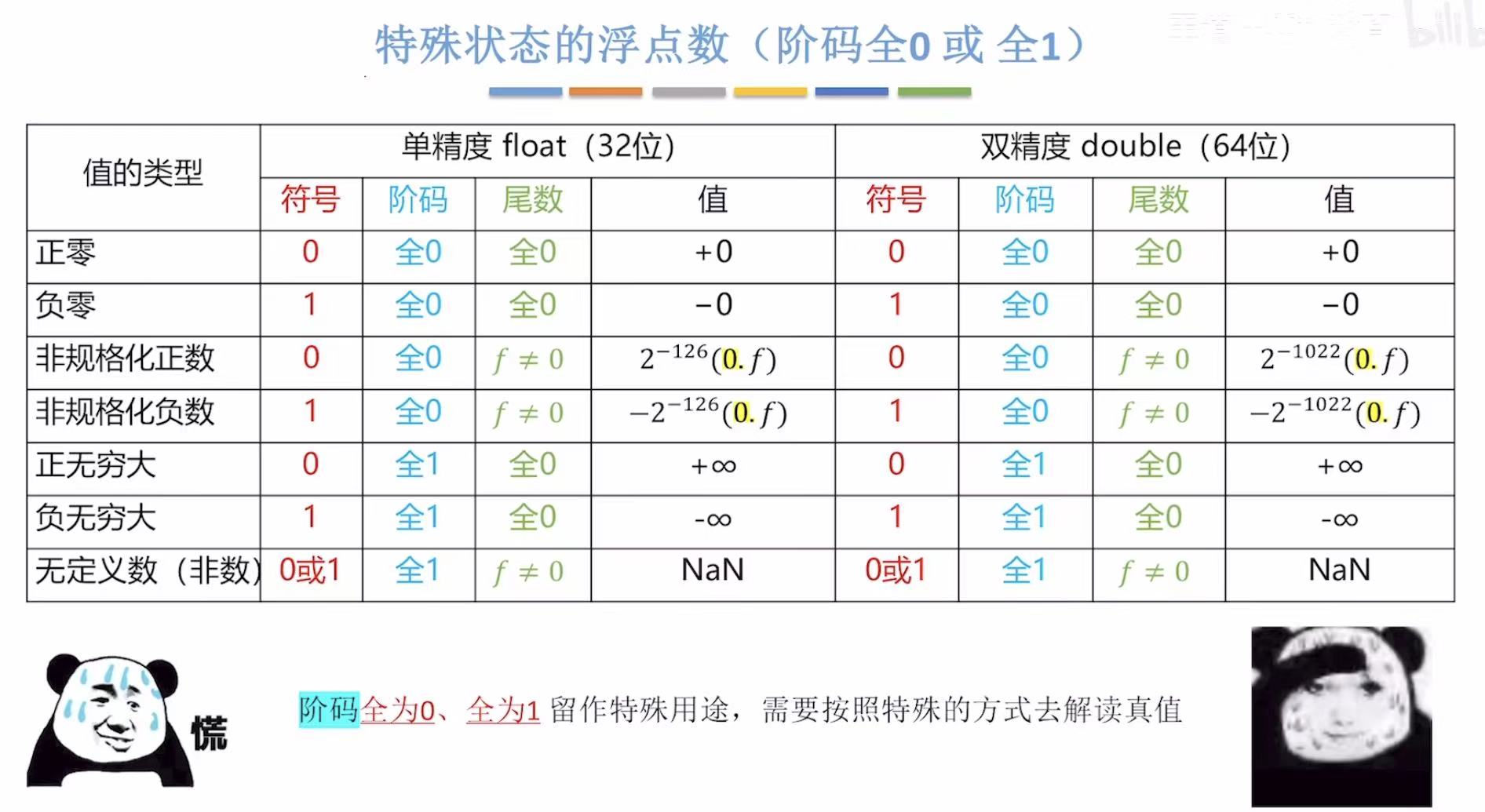
2. 规格化浮点数
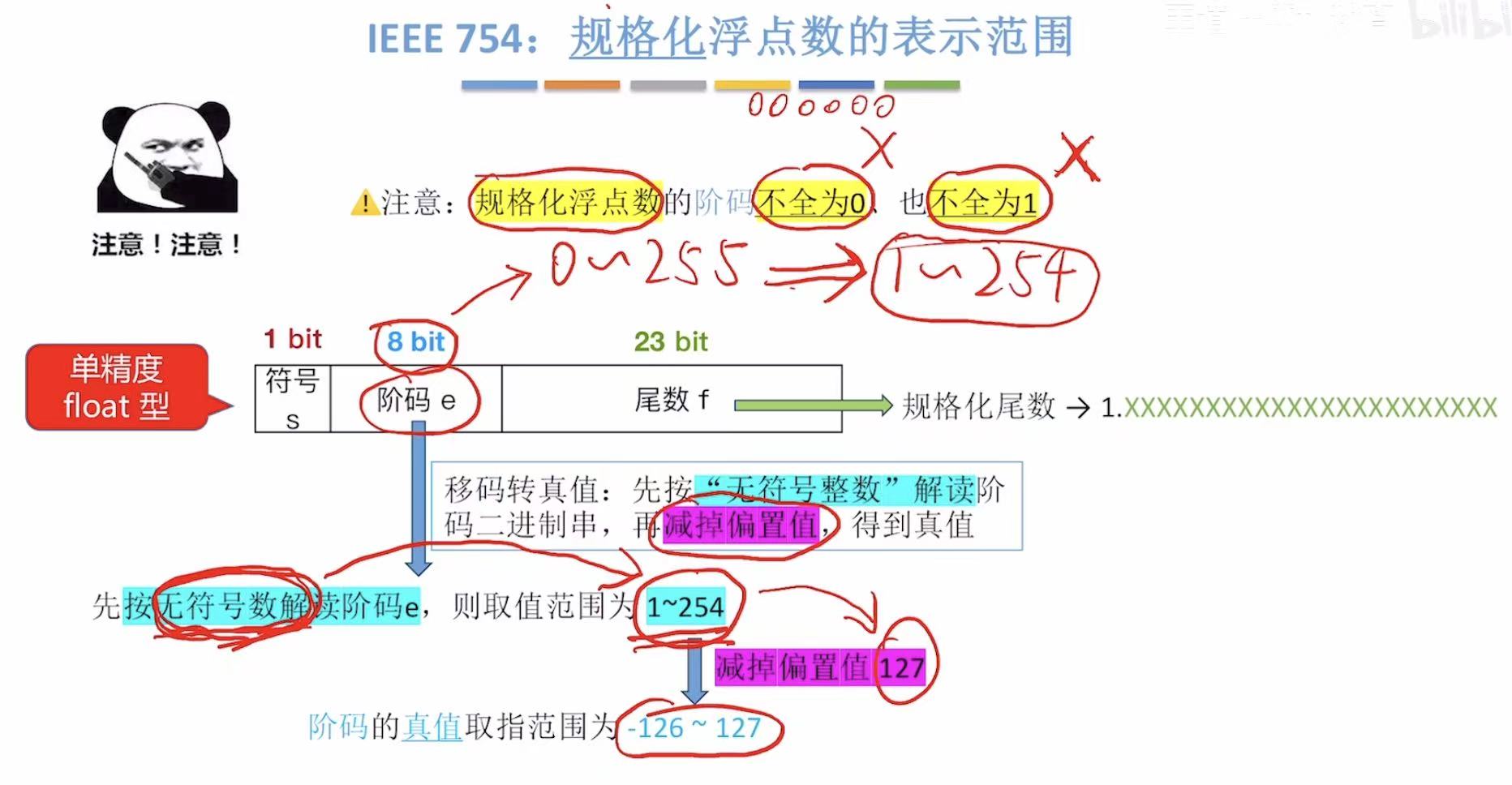
规格化浮点数就是正负数轴上的中间位置,左边儿有特殊情况,右边儿也有特殊情况。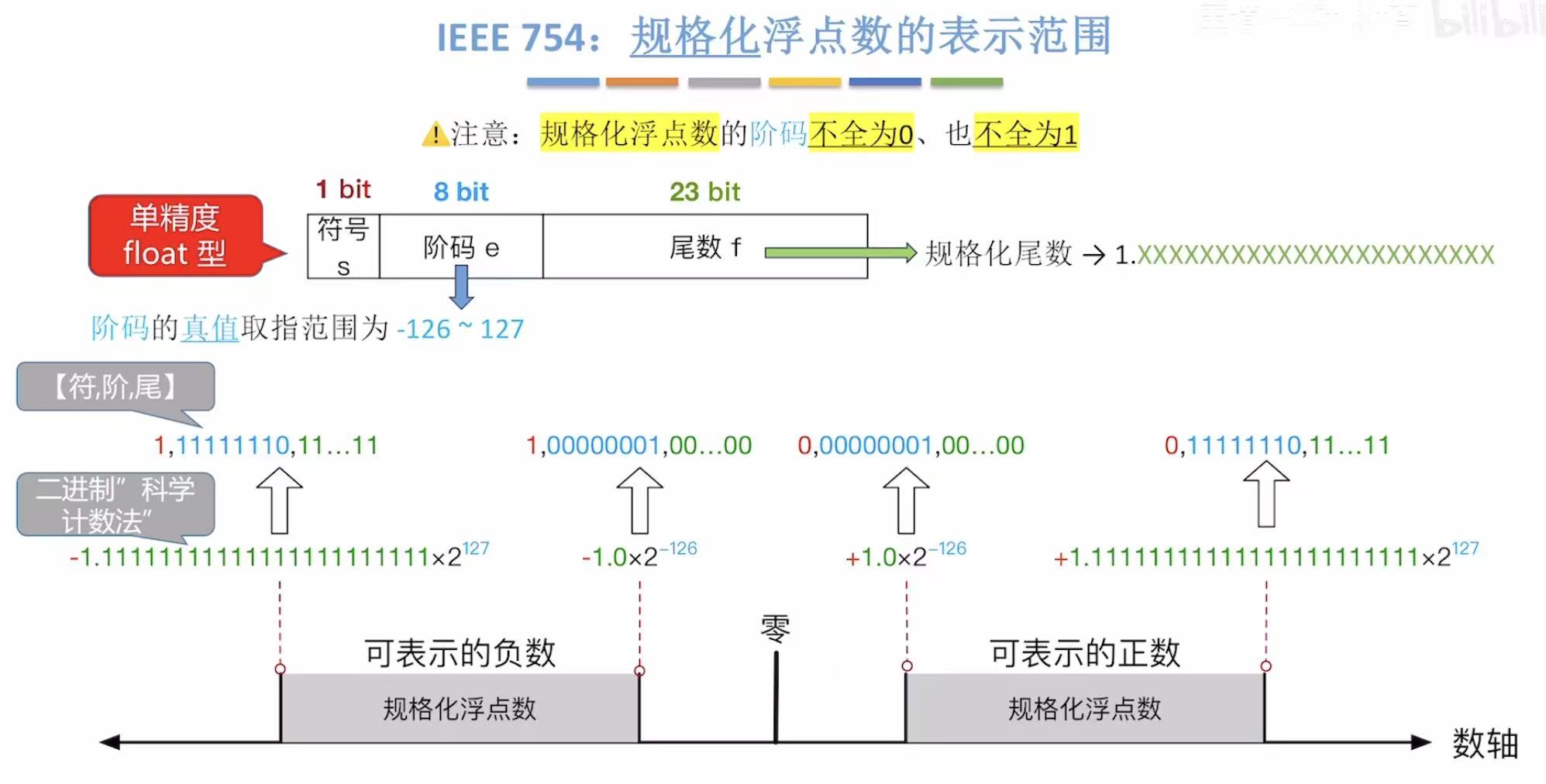
2.1 上溢
就是数轴上趋于无限的部分。
无穷大的表示
对标高数中的正无穷大和负无穷大。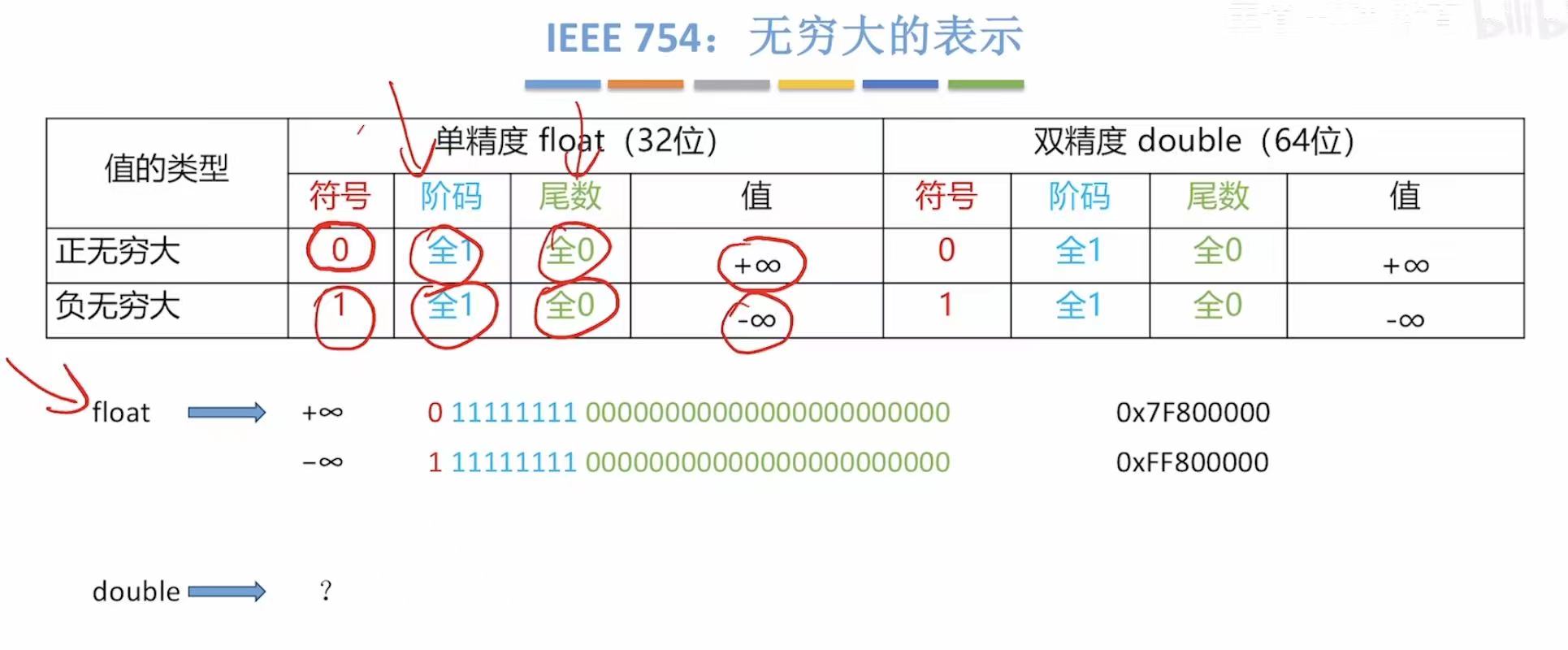

2.2 下溢
就是正负数轴上趋于0的部分。
下溢中囊括非规格化的数。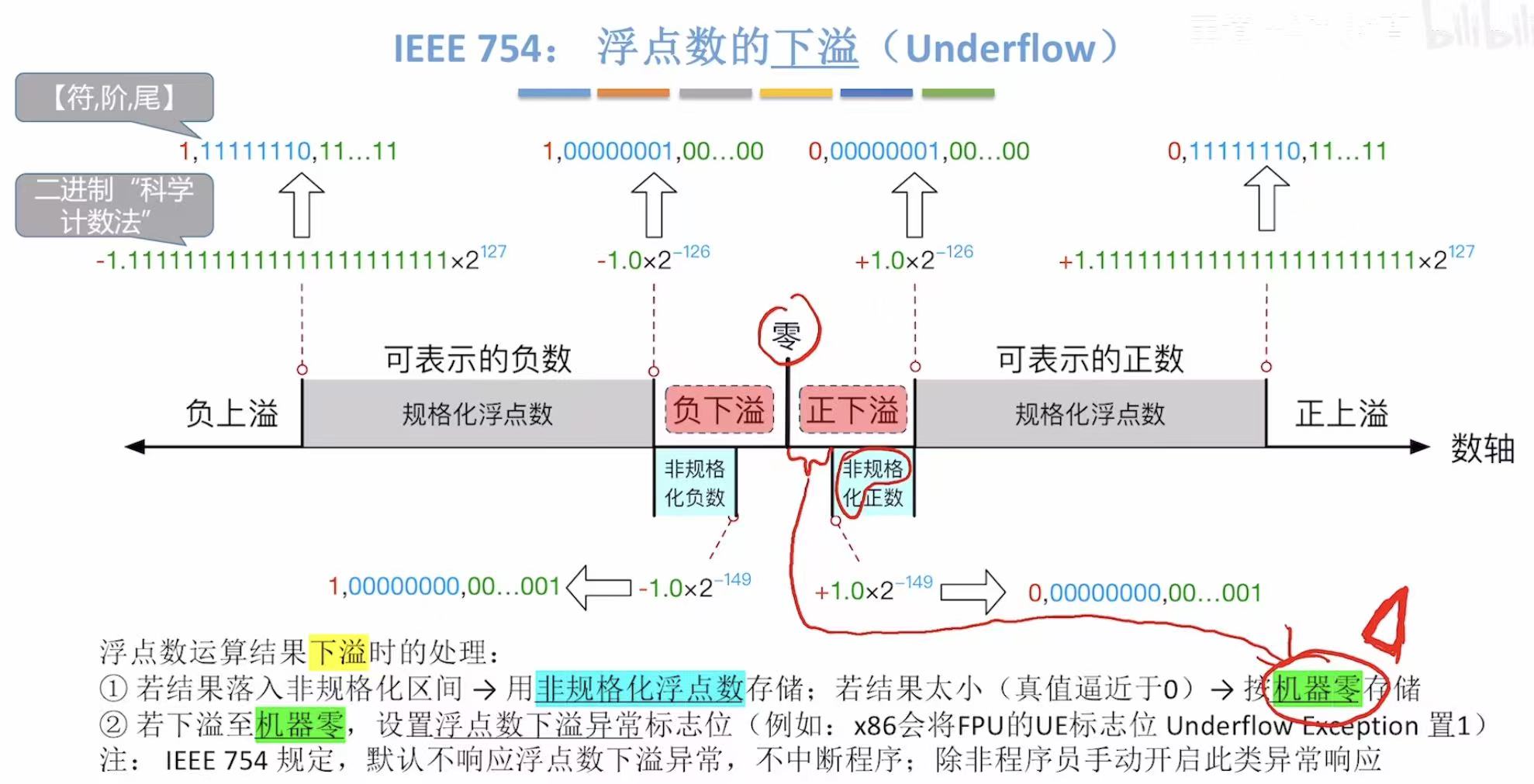
真值0的表示
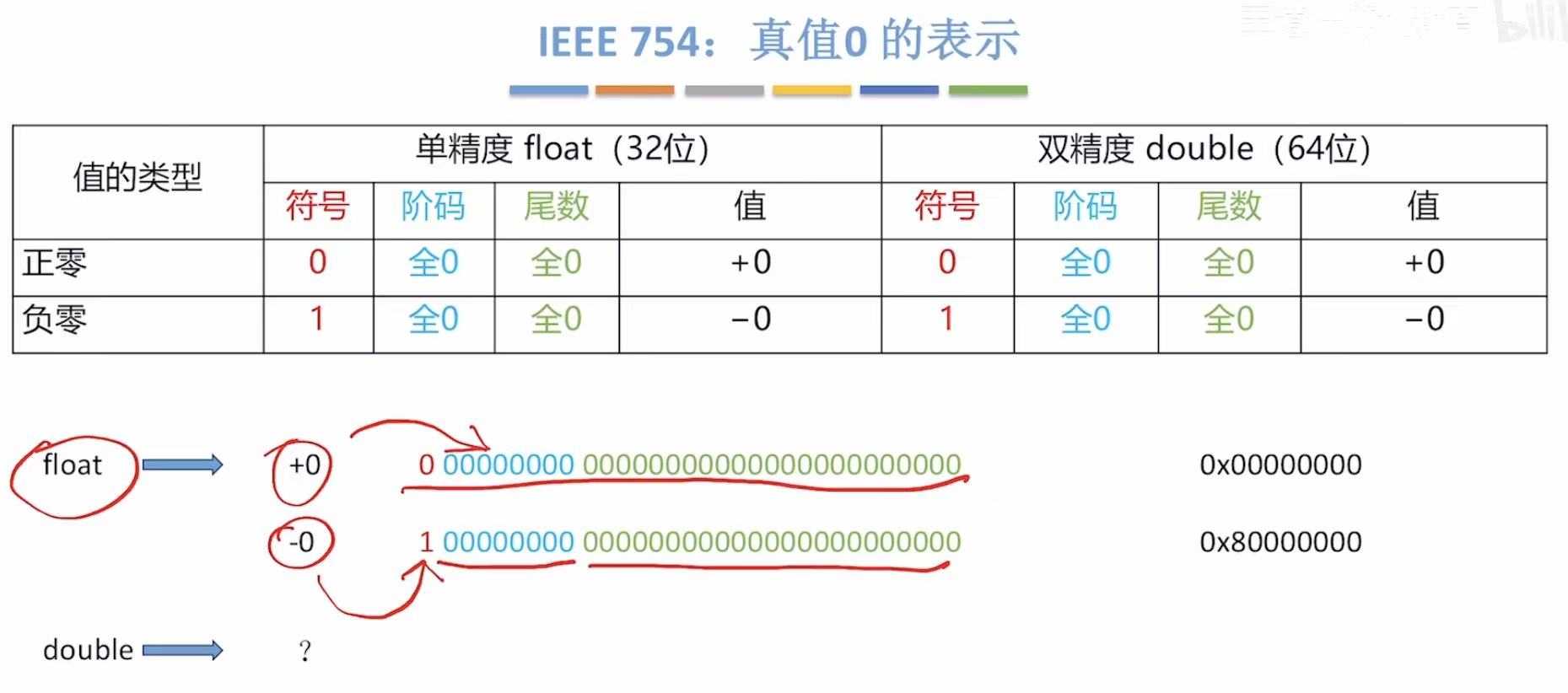
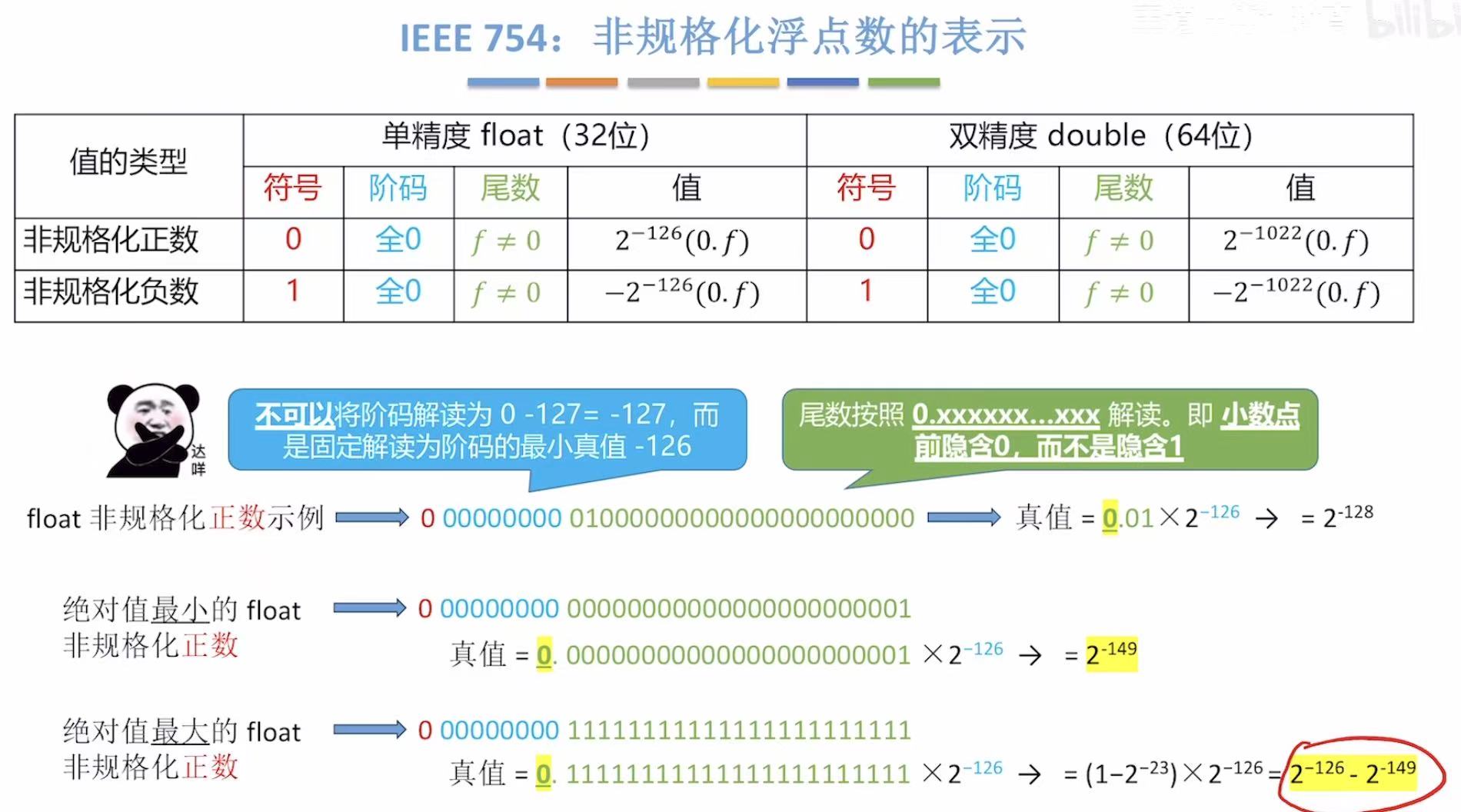
3. 非规格化浮点数
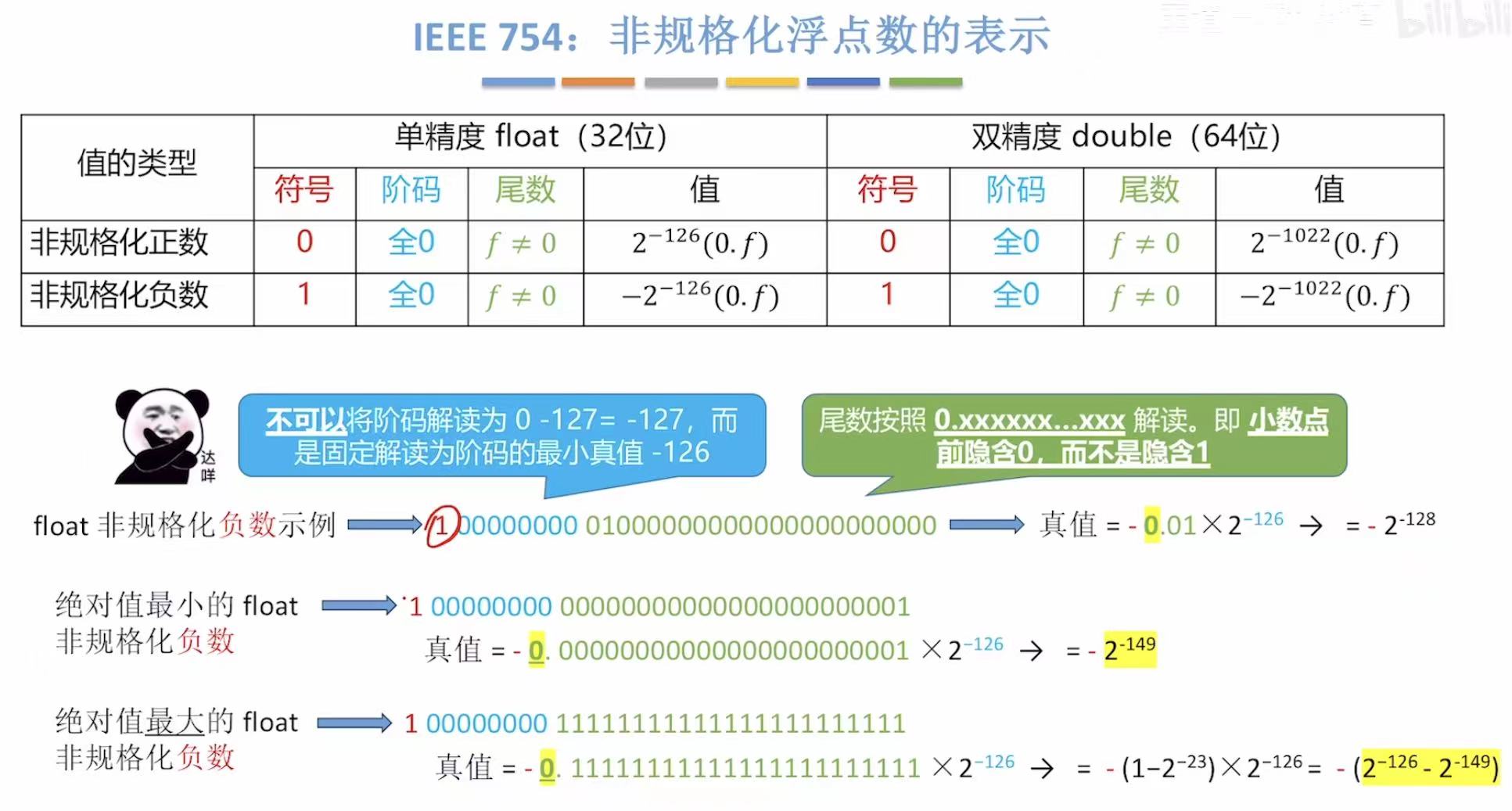
真题训练:
非数的表示
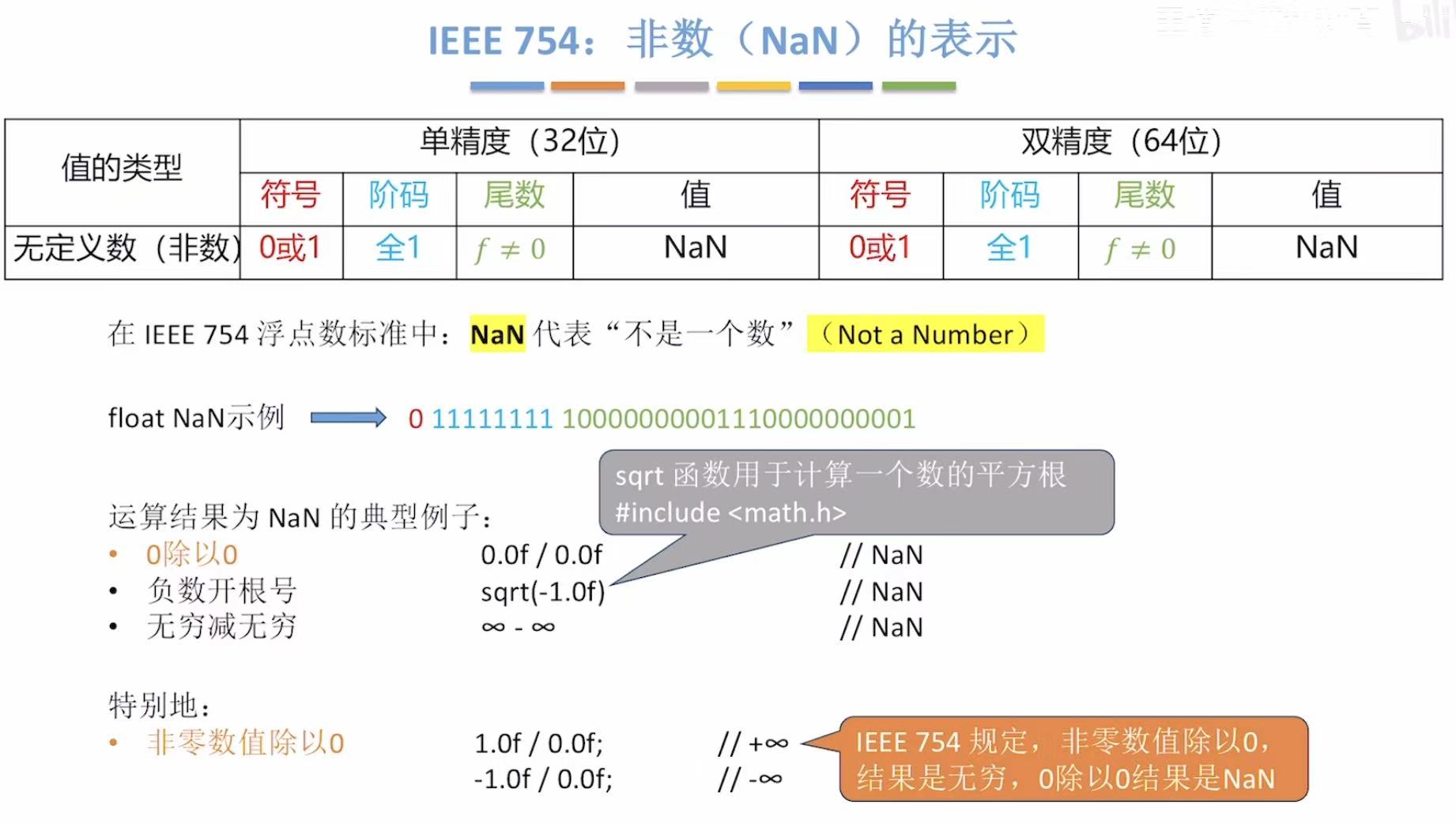
4. 小结
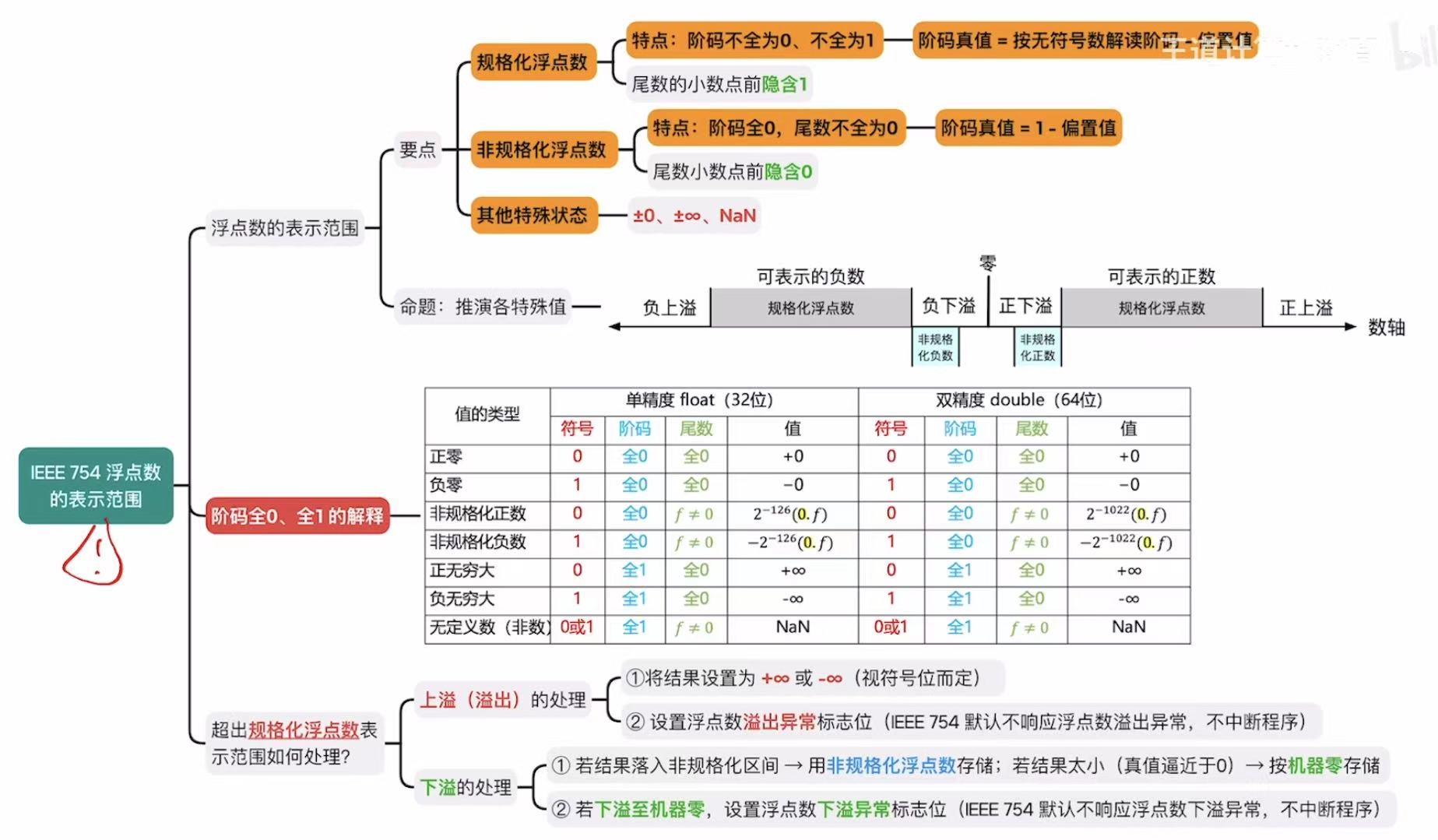
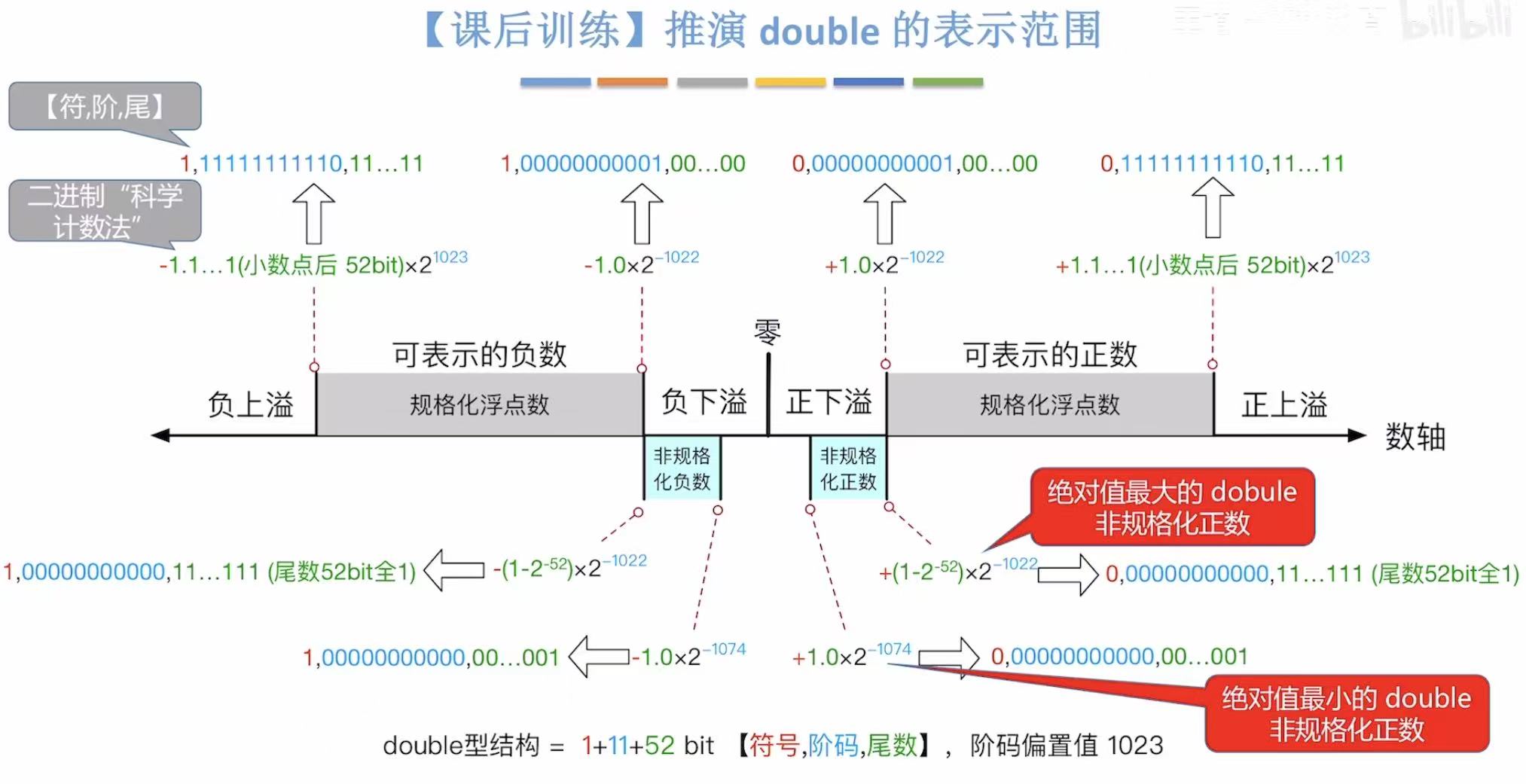
5. 补充

数据的存储和排列
1. 大小端模式
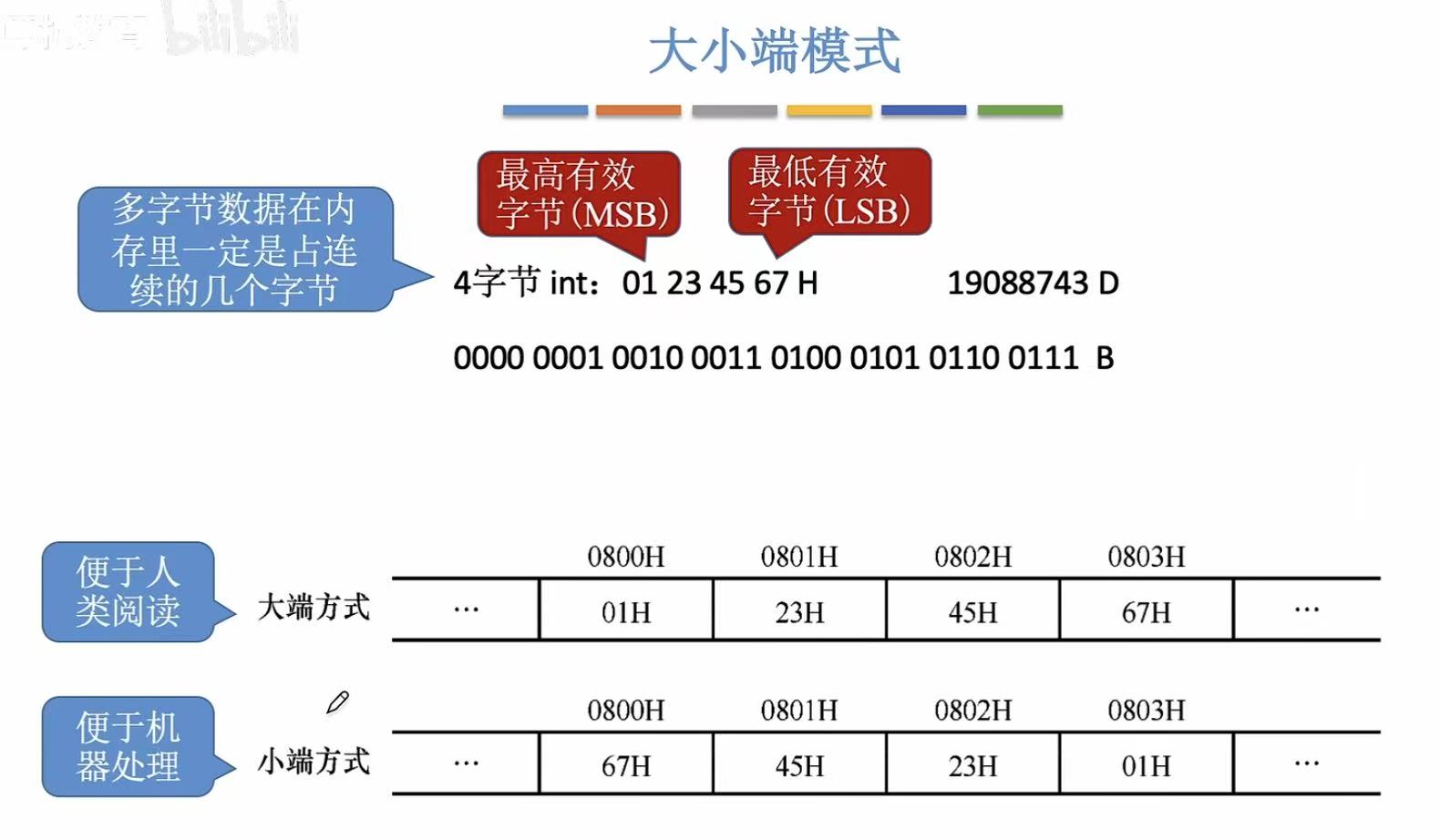
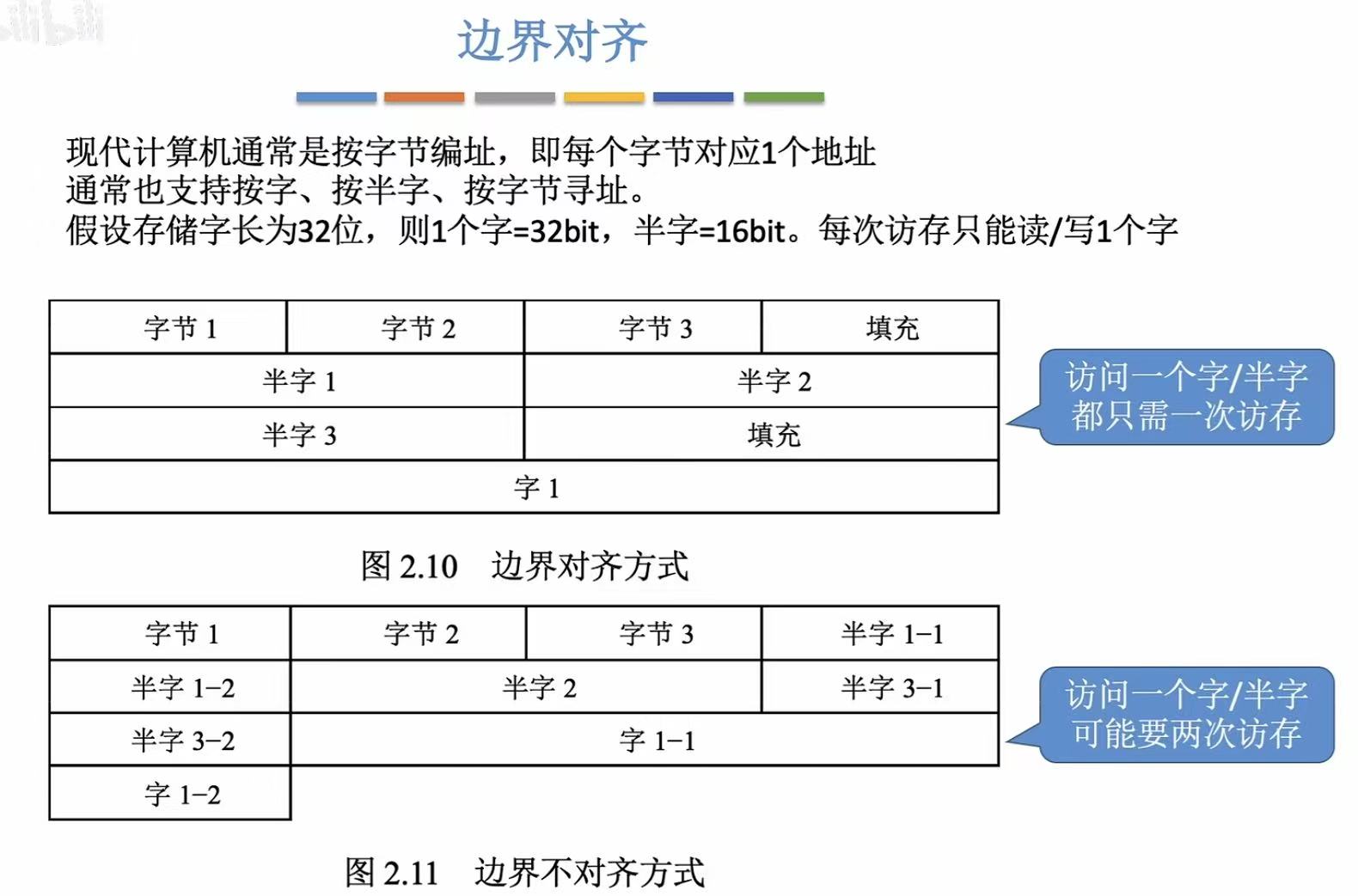
2. 边界对齐






 浙公网安备 33010602011771号
浙公网安备 33010602011771号