目录
一、前言
开篇直指:从开环到闭环,为什么最后都走向 PID
1.1 自动控制里,架构大致分两类
1)开环控制(Open-loop)
只根据“事先算好的指令”去执行,不看结果。
开环控制示意图:

2)闭环控制(Closed-loop)
一边执行,一边“看结果、算偏差、再纠正”。
闭环控制示意图:
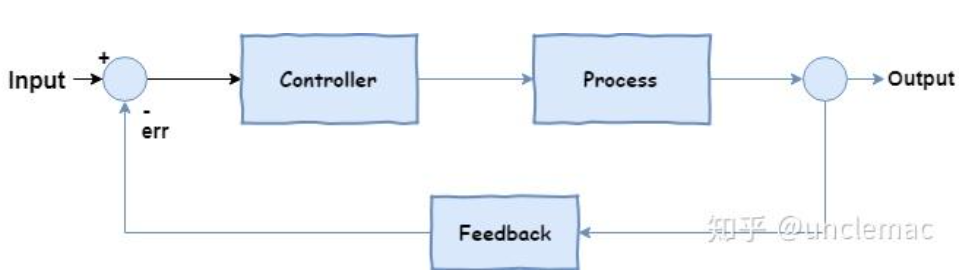
在几乎所有闭环控制系统中,只要是单输入单输出、目标是“跟着设定值走”,都会碰到一个经典算法:PID 控制。
3)PID 的三部分含义
P(Proportional,比例):按误差大小“成比例”给控制量
I(Integral,积分):累计误差,消除长期偏差
D(Derivative,微分):看误差“变化趋势”,提前刹车、抑制过冲
PID控制示意图:
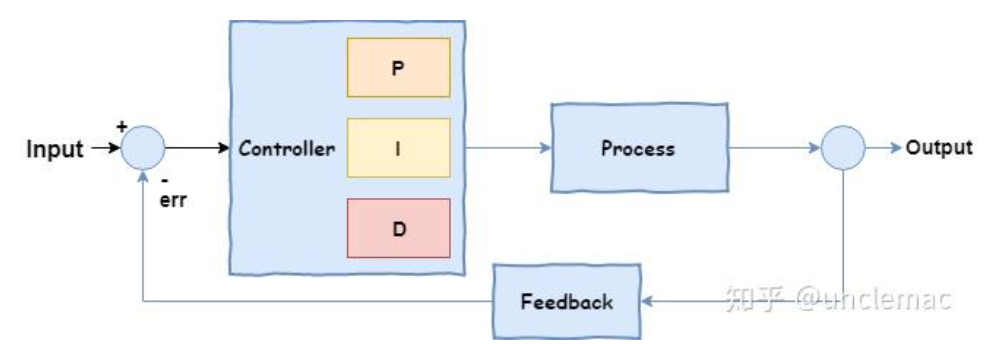
PID 的厉害之处在于:只靠这三个容易算子,就能把绝大多数工业对象调得“又快又准、还凑合稳”,而且建立简单,工程师可以靠经验就调出不错的效果,所以至今仍然是工业控制里的绝对主角。
二、开环控制(只有计划,没有纠偏)
2.1 小明蒙眼走路:典型的开环
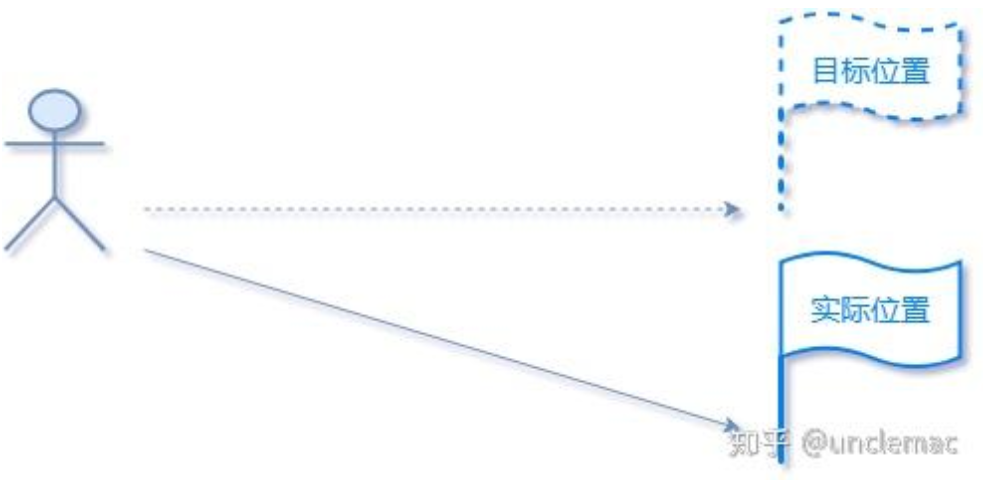
小明被蒙上眼睛,需要从起点走到 10 米外的目标旗帜。
他的大脑先“算好”——比如自己每步 0.8 米,想走 10 米,大概要走 12~13 步。
然后他闭着眼,一口气走完这些步数。
1)从控制角度看:
Input(输入):目标距离 10 m
Controller(控制器):小明大脑——算步数 N
Process(被控对象):腿——执行 N 步
没有 Feedback(反馈):中途不看自己走到哪了
2)问题:
小明步长并不是每次都一样;
地面可能有坡度、摩擦不同;
中间可能踩偏了一点方向。
所以最后停下来的位置,很大概率不是 10 m 精准位置某个偏离目标的点就是,而
开环控制的特点:
计算一次 → 执行到底 → 过程中不纠错
优点:简单、快速、成本低
缺点:完全不能自动纠偏,对干扰和模型误差非常敏感
三、闭环控制
看一眼结果再决定下一步
3.1 小明重见光明:闭环的引入
通过现在把小明眼罩摘掉,让他能够随时看到目标和自己所在的位置:
目标告诉他:“旗子在 10 米处” →给定值 r
小明走了一会儿,低头一看:“现在大概在 2 米位置” →当前输出 y
计算误差:
e=r−y=10−2=8 me = r - y = 10 - 2 = 8\text{ m}e=r−y=10−2=8 m大脑根据误差 e 再算下一段要走多少步 →控制量 u
再走一段 → 再看 → 再算误差 → 如此循环
1)典型的闭环结构:
输入 r:目标位置
输出 y:实际位置
误差 e = r - y
控制器 C:根据 e 计算控制量 u
被控对象 G:腿+身体,接收控制量 u,产生新输出 y
反馈:把 y 量出来(眼睛/传感器),送回去参与下一次计算
用一句话概括闭环:
“我知道我在哪儿、我要去哪儿,因此能不断调整自己。”
四、PID 控制器:闭环大脑的“标准算法”
4.1 标准 PID 数学形式
在闭环里,控制器就是“把误差变成控制量”的算法。
PID 的连续时间形式写成:
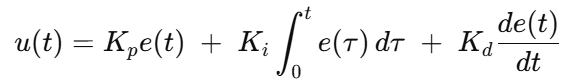
e(t)=r(t)−y(t):瞬时误差
u(t):控制器输出(给执行器的命令,比如电机电压、转矩指令等)
Kp:比例增益
Ki:积分增益
Kd:微分增益
控制器的块图可以画成:
误差 e(t) →【比例块 Kp】
→【积分块 Ki / s】
→【微分块 Kd · s】
三者相加 → 得到总控制量 u(t)
五、把 PID 放回小明故事里
还是那件事:小明要从 0 走到 10 m,设:
目标 r = 10(固定)
当前距离 y(t):小明实际走出去的位置
误差 e(t) = r - y(t):还差多少没走到
5.1 比例 P:
误差大的时候冲刺,误差小了就慢下来
设小明用纯 P 控制:
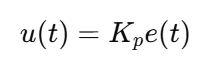
通俗一点解释:
刚起步时,误差 10 m 很大→ 误差 u 也很大 → 小明跑得比较快;
当他走到 9 m 附近时,误差变成 1 m → u 变小 → 他会自动放慢脚步。
优点:
响应直观简单:偏差大就“踩油门”,偏差小就松一点;
响应快:稍微增大 Kp,小明就跑得更积极。
缺点:
只用 P,一般会留下“稳态误差”:
比如,走到 9.7 m 时,误差只有 0.3 m,产生的控制量可能不够大,小明“懒得再迈完整一步”,最后就停在 9.7 m 左右,不会精确到 10 m。Kp 调太大,系统容易震荡甚至发散(小明来回跨大步,走过头再往回走)。
5.2 积分 I
不允许长期偏差,迟早要把账算清
积分项:
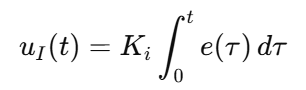
它干的事是:把误差随时间累加。哪怕误差很小,只要时间够久,积分值也会变大,最终产生足够的控制量,把误差“压到 0”。
在小明的比喻里:
如果他一直停在 9.7 m,不往前挪,说明还有 0.3 m 的误差;
积分项会一直累加这个 0.3 m;
再迈一小步;就是累到一定程度,就相当于“大脑突然意识到:好像还有点距离没走够”,于
这样就消除了 P 控制留下的稳态误差,让最终位置真的靠近 10 m。
优点:
消除稳态误差:确保长时间后误差趋近于 0。
缺点(入门先感性认识):
对误差累得太狠会“超调”:走过头再回来;
出现所谓“积分饱和”:长期大误差时代码里积分累太大,即使后面误差变 0 或反号,积分项还会拖后腿,导致系统要很久才能拉回来。
5.3 微分 D:
提前刹车,抑制过冲
微分项:
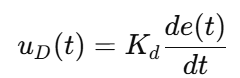
代表误差变化的斜率。它关心的是:
“误差是在快速变小,还是变大?变化速度有多快?”
当小明离目标还有一点点距离时,误差 e 哪怕不大,但下降得很快(走得很急),
此时 de/dt <0,因此:
PID 总输出:
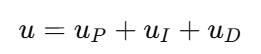
其中 uD 把总输出往下拉(相当于踩刹车)。
:在接近目标前,系统自动“减速”,从而就是结果就抑制过冲。
直观理解:
P:看到“你离目标还差 3 m”,所以踩油门;
D:看到“你靠近目标的速度太快了”,所以告诉你“赶紧松油门甚至踩刹车”。
优点:
抑制过冲,改善动态性能;
在变化剧烈的时候给出“刹车信号”。
缺点:
对噪声敏感:微分本质上是“高频放大器”,传感器有微小抖动时,D 项可能疯狂抖动,于是工程上一般不会给 Kd 调太大,还会加滤波。
六、P / I / D 三者分工(图表)
| 环节 | 数学形式 | 核心作用 | 优点 | 典型副作用 |
|---|---|---|---|---|
| P | Kp * e | 误差越大,动作越大 | 结构简单、响应速度快 | 稳态误差难以消除,Kp 大会振荡 |
| I | Ki * ∫edt | 对误差进行积累 | 消除稳态误差 | 易产生超调、振荡、积分饱和 |
| D | Kd * de/dt | 看误差变化趋势 | 抑制过冲,改善动态性能 | 对噪声敏感,Kd 过大会抖动 |
配合一句好记的总结:
P 决定“敢不敢冲”,I 决定“冲到准不准”,D 决定“要不要刹车”。
七、总结
学习完本章,应该能够解决:
画出基本闭环结构图
能指出:参考输入 r、被控量 y、误差 e、控制器 C(s)、被控对象 G(s)、反馈环节。写出标准 PID 公式
连续形式:
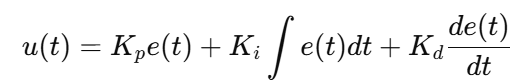
用“小明走 10 m”的故事,口头讲清楚 P / I / D 如何影响运动过程
只用通俗语言,也能讲清楚:
只有 P:会快,但可能停在 9 m 或 9.5 m,收不回来。
加了 I:能慢慢推到 10 m,误差被“算总账”消了掉。
加了 D:快到 10 m 前提前减速,不会冲到 11 m 再回来。
直觉上理解“参数调大/调小”会发生什么
Kp 太小:慢吞吞、软趴趴;Kp 太大:快但容易晃。
Ki 太小:残余误差消不干净;Ki 太大:超调、振荡更明显。
Kd 合适:曲线更平顺;Kd 过大:噪声放大,抖动明显。
本文参考:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号