图像处理中的滤波可分为低通滤波（平滑、去噪）和高通滤波（增强细节、检测边缘）。索贝尔（Sobel）算子是图像处理中最常用的高通滤波算子之一，它通过卷积强调灰度变化较大的区域，从而提取图像的边缘特征。

基本原理

概念

高通滤波是一种允许高频信息通过、抑制低频信息的图像滤波操作。

  • 低频：图像中变化缓慢的区域，例如大片的天空、平滑的墙面。
  • 高频：图像中变化剧烈的部分，如边缘、纹理、噪声。

高通滤波通常用于：

  • 边缘检测
  • 纹理增强
  • 图像锐化
  • 特征提取

从空间域角度看，高通滤波就是利用带有正负值的卷积核对图像进行卷积，使灰度变化突出的区域被放大。

卷积核示例

常见高通滤波核包括：

锐化核：
  0 -1  0
 -1  5 -1
  0 -1  0
拉普拉斯算子：
  0 -1  0
 -1  4 -1
  0 -1  0

它们都包含正负系数，使得：

  • 区域灰度变化越大，其卷积结果越大；
  • 平滑区域（低频）结果趋近 0 ，被抑制。

索贝尔算子也属于典型高通滤波，通过一阶微分检测梯度。

索贝尔（Sobel）算子原理

梯度与边缘的关系

图像的边缘对应像素灰度的急剧变化区域，而灰度变化可用**梯度（Gradient）**衡量。

二维图像梯度定义：

Gx = ∂I/∂x   （水平变化）
Gy = ∂I/∂y   （垂直变化）

边缘强度：

G = sqrt(Gx^2 + Gy^2)

索贝尔算子就是通过近似求一阶偏导数，从而检测边缘方向和强度。

数学卷积核

水平 Sobel（检测垂直边缘）

Gx =
[-1  0  +1
 -2  0  +2
 -1  0  +1]

为什么能检测垂直边缘？

观察这两个区域：

左侧像素 * (-1 -2 -1)
右侧像素 * (+1 +2 +1)

也就是说：

  • 右侧像素亮、左侧像素暗 → 结果为正（正梯度✔）
  • 左侧像素亮、右侧像素暗 → 结果为负（负梯度✔）
  • 左右差别越大 → 响应越强 → 垂直边缘更明显

垂直 Sobel（检测水平边缘）

Gy =
[-1 -2 -1
  0  0  0
 +1 +2 +1]

为什么能检测水平边缘？

  • 上方像素与下方像素做加权差分
  • 如果上暗下亮 → Gy 大（正）
  • 如果上亮下暗 → Gy 大（负）

即：

上方像素 * (-1 -2 -1)
下方像素 * (+1 +2 +1)

→ 上下差值越明显，水平边缘越强。

特点

  • 核心思想是一阶微分 + 加权平滑
  • 3x3 卷积能够平滑噪声，比简单的 Roberts、Prewitt 更稳定
  • 对噪声不太敏感，检测边缘效果比 Roberts、Prewitt 更好

为什么 Sobel 算子仍属于高通滤波？

因为：

  • 卷积核系数中有正负符号
  • 使得边缘（高频）响应明显
  • 对低频区域卷积结果趋近于零

换句话说，Sobel = 积分平滑 + 微分增强，是典型高通滤波器。

OpenCV 中 Sobel

OpenCV 使用 cv2.Sobel() 封装卷积操作，可自动计算 Gx 或 Gy。

基本原型：

cv2.Sobel(src, ddepth, dx, dy, ksize=3)

参数说明：

  • src：输入图像
  • ddepth：输出图像深度，通常为 cv2.CV_64F 防止溢出
  • dx、dy：指定求 x 方向或 y 方向的梯度
    • dx=1, dy=0 → Gx
    • dx=0, dy=1 → Gy
  • ksize：Sobel 核大小，默认为 3，可以取 1、3、5、7

示例

使用 OpenCV 实现高通滤波与 Sobel 边缘检测。

import cv2
import numpy as np
# 读取图像并转灰度
img = cv2.imread("test.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 1. Sobel X（检测垂直边缘）
sobel_x = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=3)
# 2. Sobel Y（检测水平边缘）
sobel_y = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=3)
# 3. 计算梯度强度
sobel_mag = cv2.magnitude(sobel_x, sobel_y)
# 转换为可视化格式（0-255）
sobel_x = cv2.convertScaleAbs(sobel_x)
sobel_y = cv2.convertScaleAbs(sobel_y)
sobel_mag = cv2.convertScaleAbs(sobel_mag)
# 4. 高通滤波（锐化效果）
kernel_hp = np.array([
[0, -1, 0],
[-1, 5, -1],
[0, -1, 0]
])
highpass = cv2.filter2D(gray, -1, kernel_hp)
# 显示结果
cv2.imshow("Gray", gray)
cv2.imshow("Sobel X", sobel_x)
cv2.imshow("Sobel Y", sobel_y)
cv2.imshow("Sobel Magnitude", sobel_mag)
cv2.imshow("High-pass Sharpen", highpass)
cv2.waitKey(0)
cv2.destroyAllWindows()

执行效果：

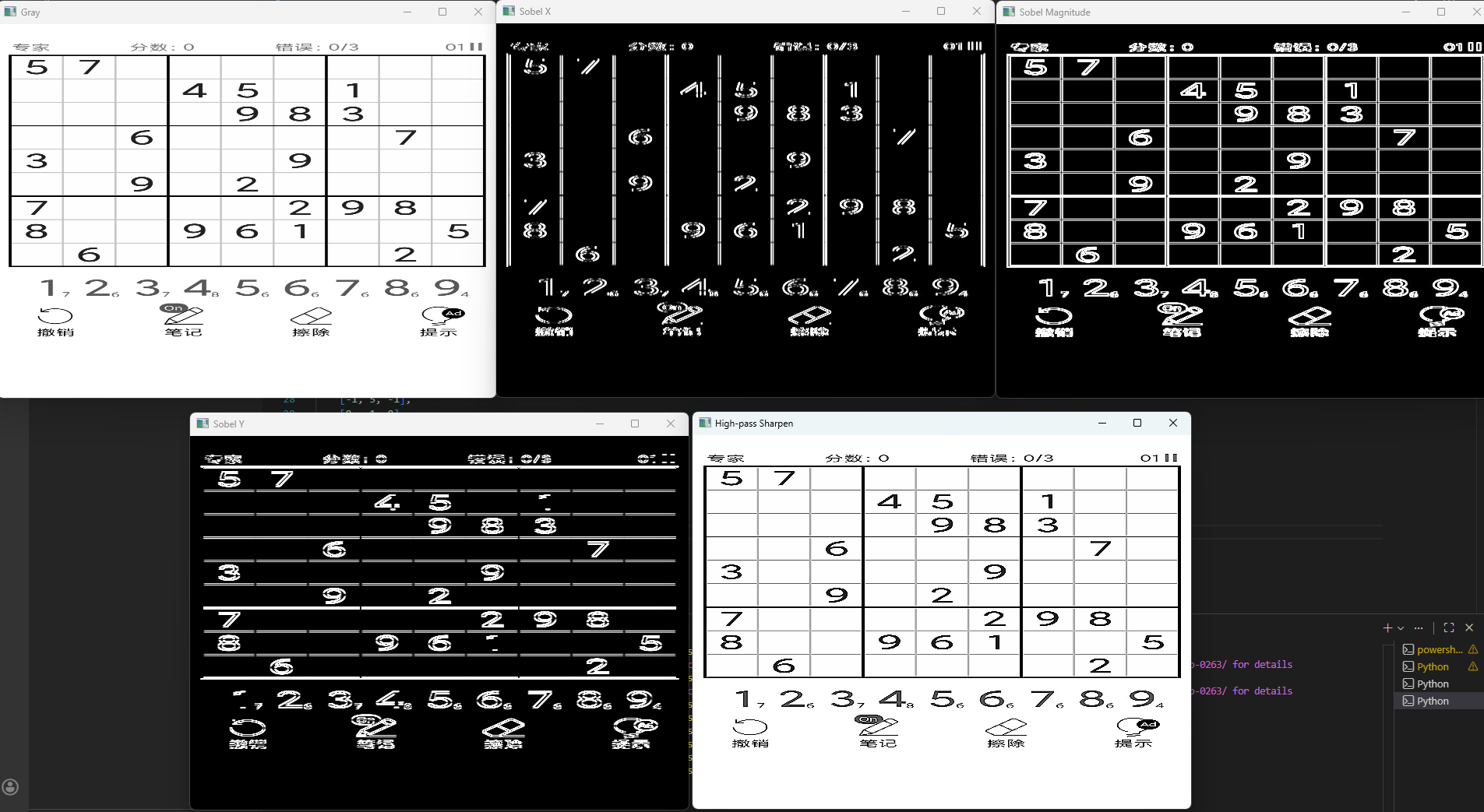
在这里插入图片描述

结果解释：

Sobel X：

  • 强调左右方向灰度变化
  • 垂直边缘清晰可见（如门框、建筑物立柱）

Sobel Y：

  • 强调上下方向灰度变化
  • 水平边缘突显（如桌面边缘）

梯度幅值（Magnitude）：

  • 综合 X、Y，形成最终边缘图
  • 与 Canny 边缘检测相比更原始但控制简单

高通锐化结果：

  • 图像整体更“清晰”
  • 细节增强，但可能引入噪声

索贝尔算子与其他边缘算子的比较

算法类型优点缺点
Roberts一阶微分简单、速度快对噪声敏感、弱平滑
Prewitt一阶微分稍优于 Roberts平滑能力不足
★Sobel一阶微分 + 平滑性价比最高、鲁棒性强不如 Canny 稳定
Laplacian二阶微分方向无关、边缘明显噪声更敏感
Canny综合方法效果最好、边缘最清晰参数较多、计算量大

总结

  • 高通滤波强调高频信息，适合边缘增强
  • 索贝尔算子通过一阶微分 + 平滑实现鲁棒的边缘检测
  • OpenCV 的 cv2.Sobel 可方便计算 Gx、Gy 和梯度幅度