《算法通关指南：算法基础篇 ---- 二维前缀和 — 1. 【模板】二维度前缀和，2.激光炸弹》

在这里插入图片描述

小龙报：个人主页
作者简介：C++研发，嵌入式，机器人方向学习者
❄️个人专栏：《C语言》《算法》KelpBar海带Linux智慧屏项目
《coze智能体开发平台》
✨ 永远相信美好的事情即将发生

在这里插入图片描述

文章目录

前言

本系列讲解算法竞赛的数据结构在算法竞赛中，我们主要关心的其实是时间开销，空间上是基本够用的，因此我们是使用庞大的数组实现的话不多说冲！

一、二维前缀和

1.1 核心问题

1.1.1 创建前缀和矩阵

创建前缀和矩阵：f[i][j] = f[i − 1][j] + f[i][j − 1] − f[i − 1][j − 1] + a[i][j]

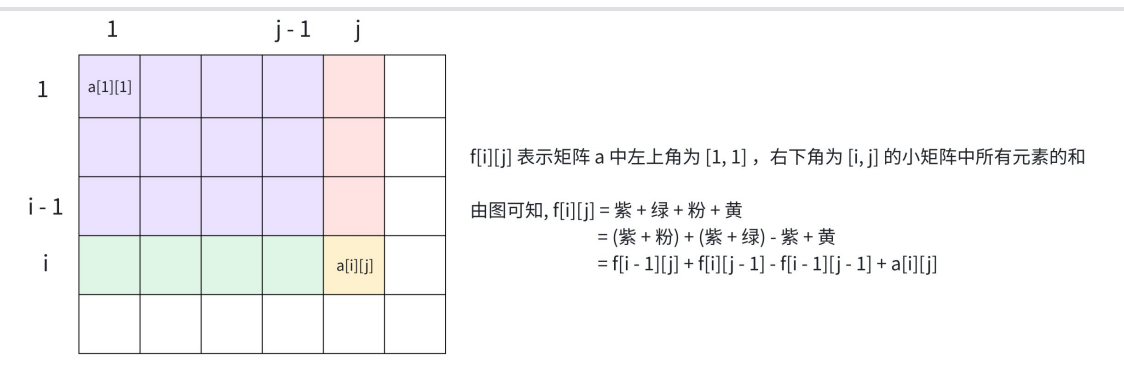
在这里插入图片描述

2.2.2 查询以(x1 , y1)为左上角,(x2 , y2)为右下角的子矩阵的和

核心公式：f[x2][y2] - f[x1 - 1][y2] - f[x2][y1-1] + f[x - 1][y1- 1]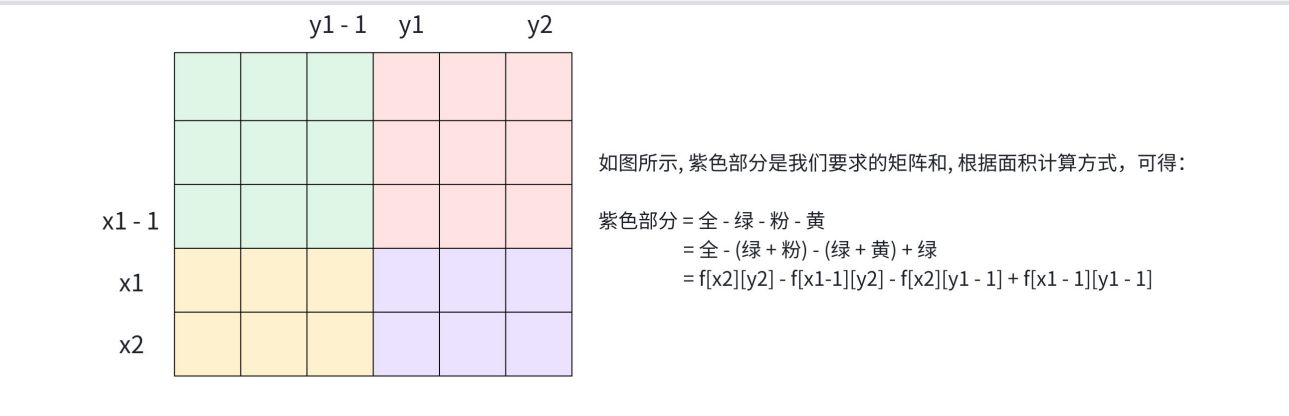
在这里插入图片描述

二、二维前缀和经典算法题

2.1【模板】前缀和

2.1.1题目

链接：【模板】二维度前缀和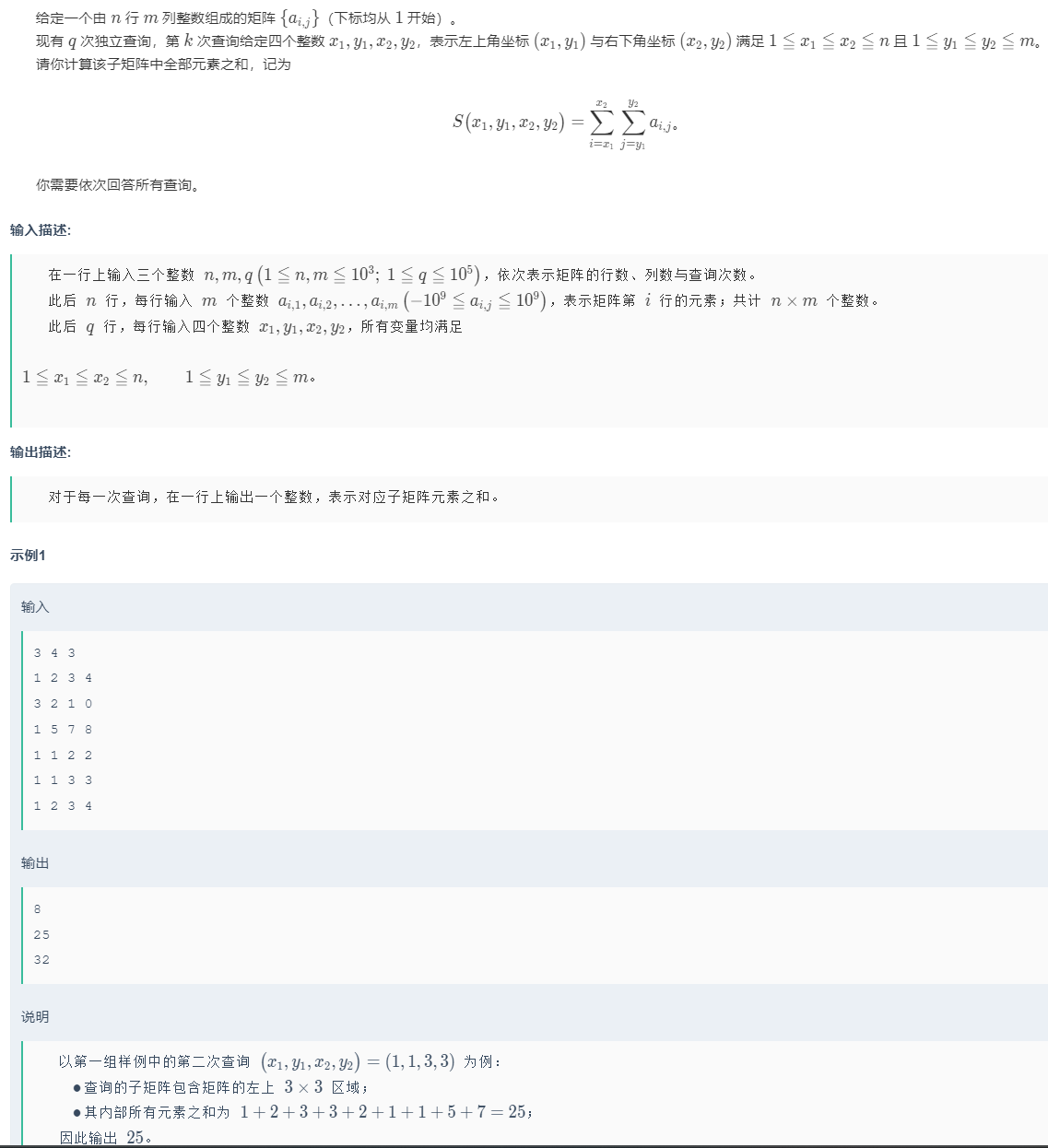
在这里插入图片描述

2.1.2 算法原理

依照刚才讲解前缀和原理模拟即可

2.1.3代码

#include <iostream>
  using namespace std;
  typedef long long LL;
  const int N = 1010;
  LL f[N][N];
  int main()
  {
  int n, m, q;
  cin >> n >> m >> q;
  for (int i = 1; i <= n; i++)
  {
  for (int j = 1; j <= m; j++)
  {
  LL x;
  cin >> x;
  f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;
  }
  }
  while (q--)
  {
  int x1, y1, x2, y2;
  cin >> x1 >> y1 >> x2 >> y2;
  cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1] << endl;
  }
  return 0;
  }

2.2 激光炸弹

2.2.1 题目

链接：激光炸弹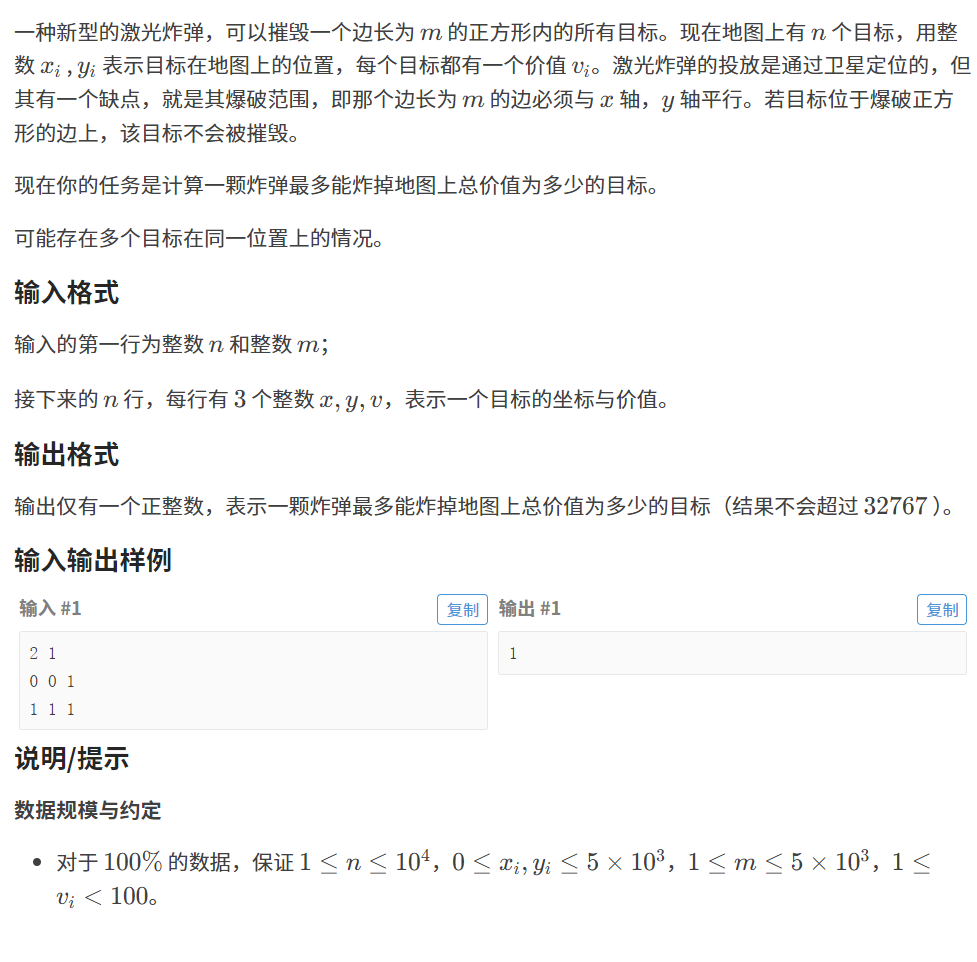
在这里插入图片描述

2.2.2 算法原理

可以用一个二维矩阵将所有目标的价值存起来，其中a[i][j] 表示[i, j] 位置的目标价值之和。
一颗炸弹能够获得的价值正好是一个R × R的一个正方形内所有目标的价值总和，那么我们可以求出矩阵的前缀和矩阵，然后枚举所有边长为R 的子正方形的价值之和，求出里面的最大值即可。
解决两个核心问题：
（1）如何枚举边长为R 的所有正方形：
• 仅需枚举右下角[x2 , y2 ] (R + 1 ≤ x2 ≤ 5000, R + 1 ≤ y2 ≤ 5000) ，那么结合边长， 就可算出左上角[x2 − R + 1, y2 − R + 1] 。

• 代入前缀和矩阵中，就可以快速求出这个正方形内所有目标的总价值。
（2）细节问题：
•题目中某⼀个位置会「重复」出现，因此a[i][j]+ = w ；
• 半径R 可能「超过5000 」，此时炸弹可以摧毁所有目标，也就是整个矩阵的目标价值之和。

2.2.3 代码

#include <iostream>
  #include <cmath>
    using namespace std;
    const int N = 5010;
    int f[N][N];
    int a[N][N];
    int n, m;
    int main()
    {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
    int x, y, v;
    cin >> x >> y >> v;
    x++, y++;
    a[x][y] += v;
    }
    n = 5001;
    for (int i = 1; i <= n; i++)
    {
    for (int j = 1; j <= n; j++)
    f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
    }
    int ret = 0;
    m = min(m, n);
    for (int x2 = m; x2 <= n; x2++)
    {
    for (int y2 = m; y2 <= n; y2++)
    {
    int x1 = x2 - m + 1;
    int y1 = y2 - m + 1;
    ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]);
    }
    }
    cout << ret << endl;
    return 0;
    }

总结与每日励志

✨本文介绍了二维前缀和的核心概念与应用，包括如何构建前缀和矩阵（公式：f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + a[i][j]）以及查询子矩阵和的快速计算方法。通过两道经典算法题（模板题和激光炸弹）演示了实际应用，强调正确处理边界条件和重复值的重要性。文章最后以励志话语作结，鼓励读者坚持学习算法编程。
在这里插入图片描述