【你奶奶都能听懂的C语言】第10期 快速幂+离散化+递归+归并排序(分治)
开头:
ok了,今天继续我们的实战篇,如标题,这一期依旧介绍算法,也会配合例题
快速幂
如其名,所谓快速幂,就是一种高效计算整数幂的算法,其核心是将幂次拆解为二进制,通过 “平方+乘法” 的组合结果,降低求 “一个数的几次方” 的时间复杂度
来看到道例题: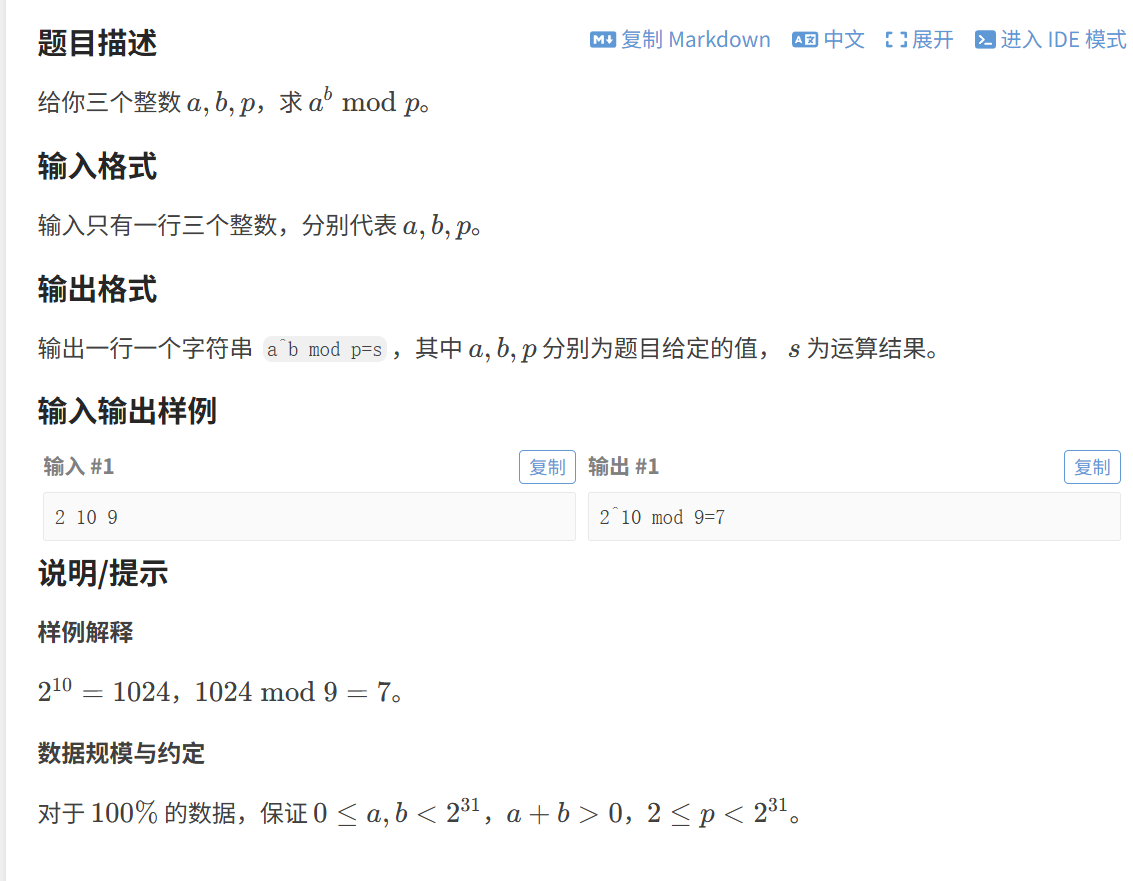
通过题目要去求 a 的 b 次方,并且对结果取 p 的模,我们可以很快的想到能够直接用一个循环或者使用 pow 库函数来求解,可是题目中的材料范围太大,这样做的话时间复杂度太大,会超时。
这时候就要利用快速幂(倍增+二进制)来解除了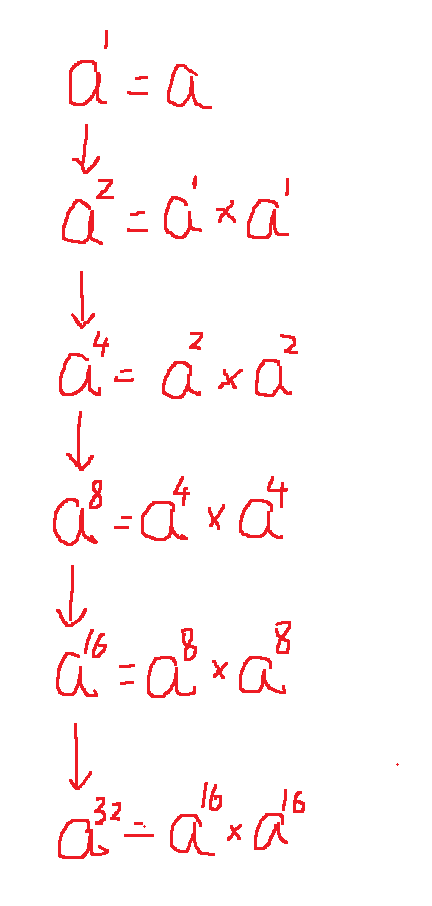
如上图,如果想求 a 的 32 次方,用普通的循环来求解的话,就要循环 32 次,而利用这种倍增思想,只需要进行 5 次,这就大大降低了时间复杂度,但是若是我想要求 a 的 11 次方怎么办呢。
这时候就要进行二进制转换,11 的二进制为 1011
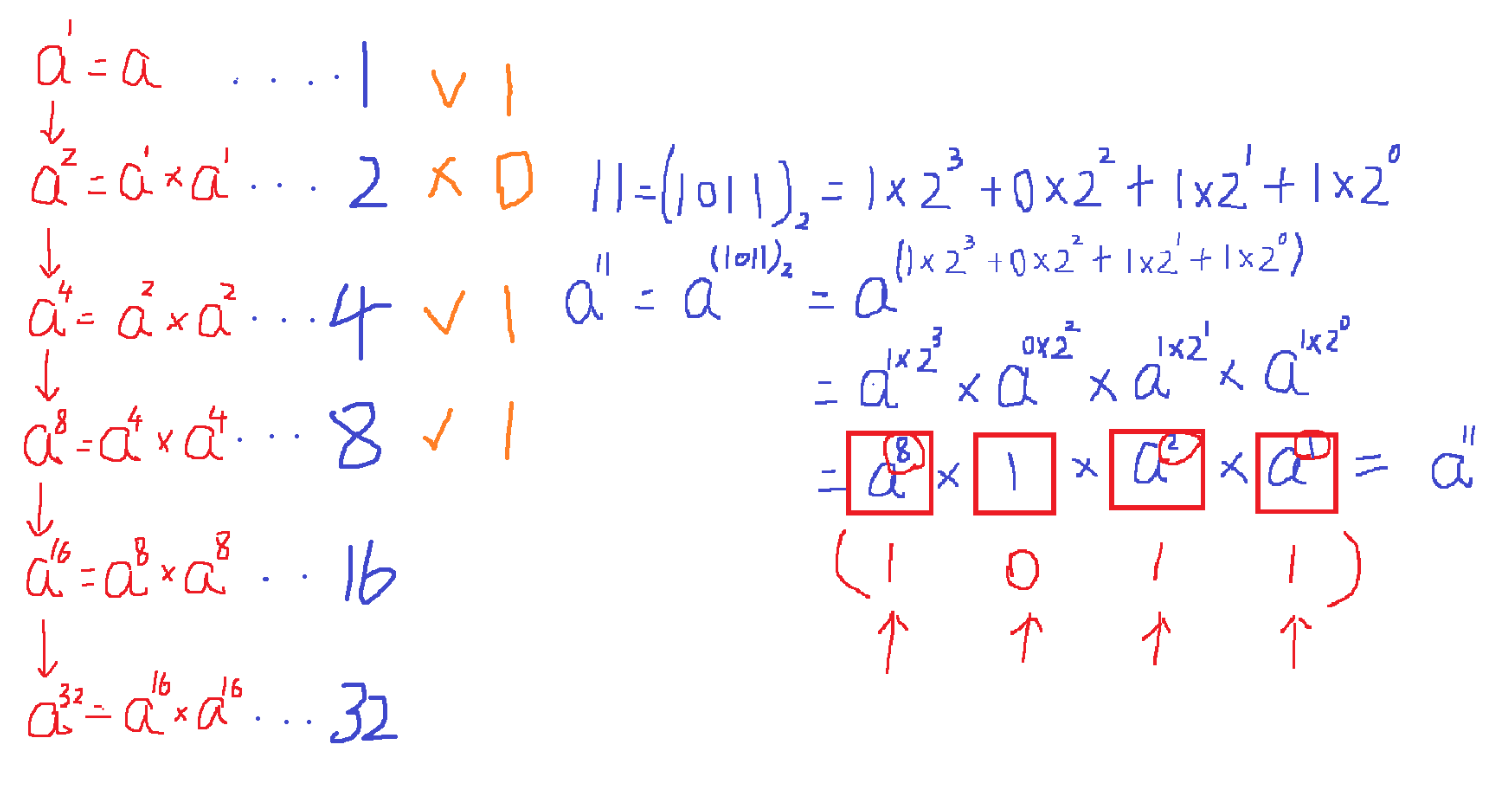
可以看到,如果要计算 11 这类数,我们许可先求它二进制数所对应的每一位权重,然后将它们相乘,就允许得到结果
我们还要解决求余数,如果算出总的结果再取模,总的结果可能会很大,这时就要使用性质:
当计算过程中,只有 “加法” 和 “乘法“ 时,可以在每一步运算后进行取模操作
我们代码实现一下: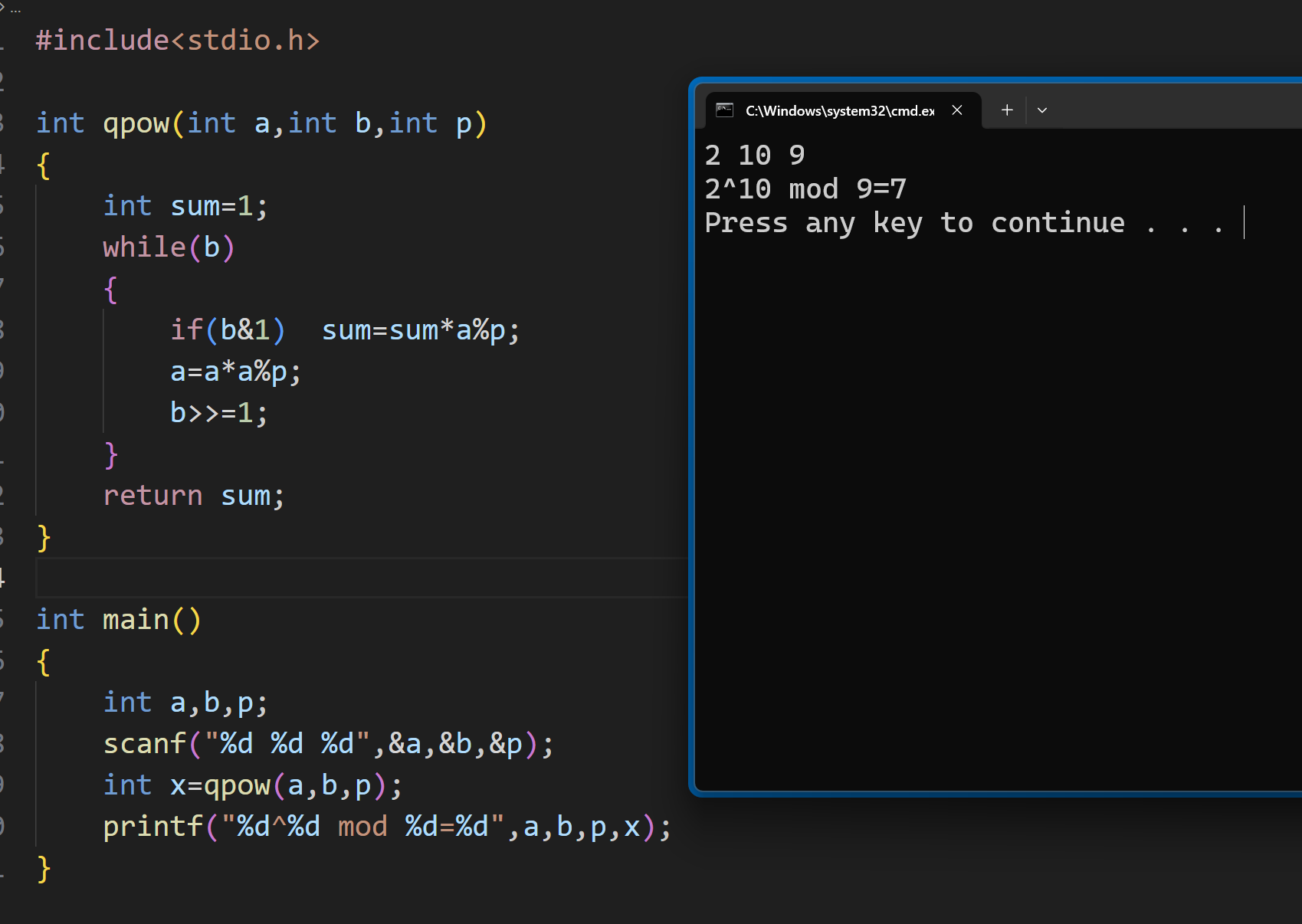
在实现快速幂函数 qpow 中,通过将 b 和 1 按位与,来得到 b 二进制中的最右边的数,如果是 1 ,那么说明这一位占有权重,就让 sum 去乘上 a ,随后的 a 需要倍增,然后将 b 左移一位,继续判断,如果 b==0 时,循环结束,返回最终结果
离散化
通过当题目中材料的范围很大,只是数据的总个数不大,此时如果需要用资料的值来映射数组下标,就能够用离散化的思想预处理一下所有的数据,使得每一个数据都映射成一个较小的值,再用离散化后的数来处理疑问。
有几个数太大了,不好直接对其进行操作,这时候大家将这些数一 一对应较小的数,用这些较小的数来进行处理,为了保证对应关系的唯一性和有理性,我们要先把数组排序,随后去重,用此时数组的下标来对应数据就是用你奶奶都能听懂的话来讲,就
先举个例子:
10
1999999
12
1999999
-48444
568
12
-100
-2845630
1000000001
263
//数出
6 3 6 1 5 3 2 0 7 4这里我们采用C++
- 方法一:排序+去重+二分查找
大家先用 sort 函数对数组进行排序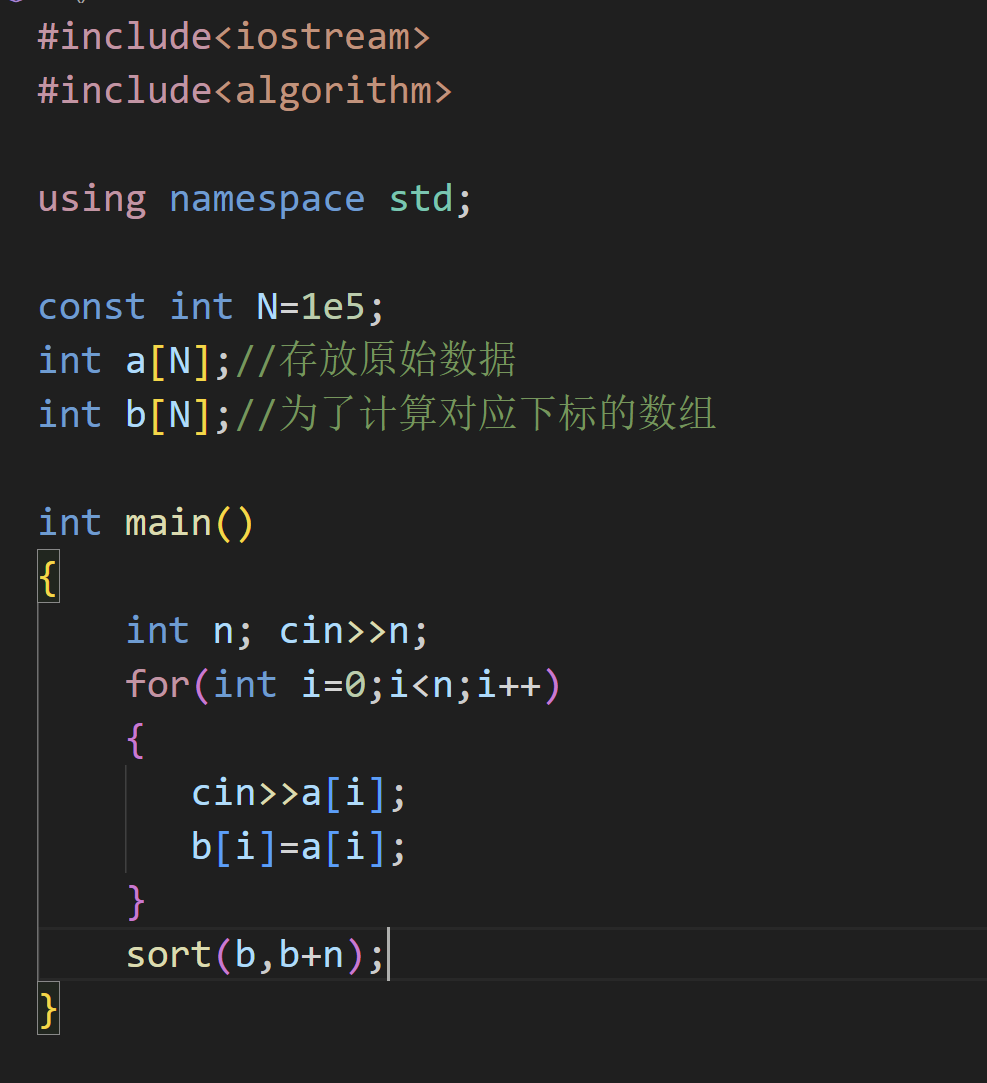
接着我们使用 unique 去重函数,它返回的是首元素下标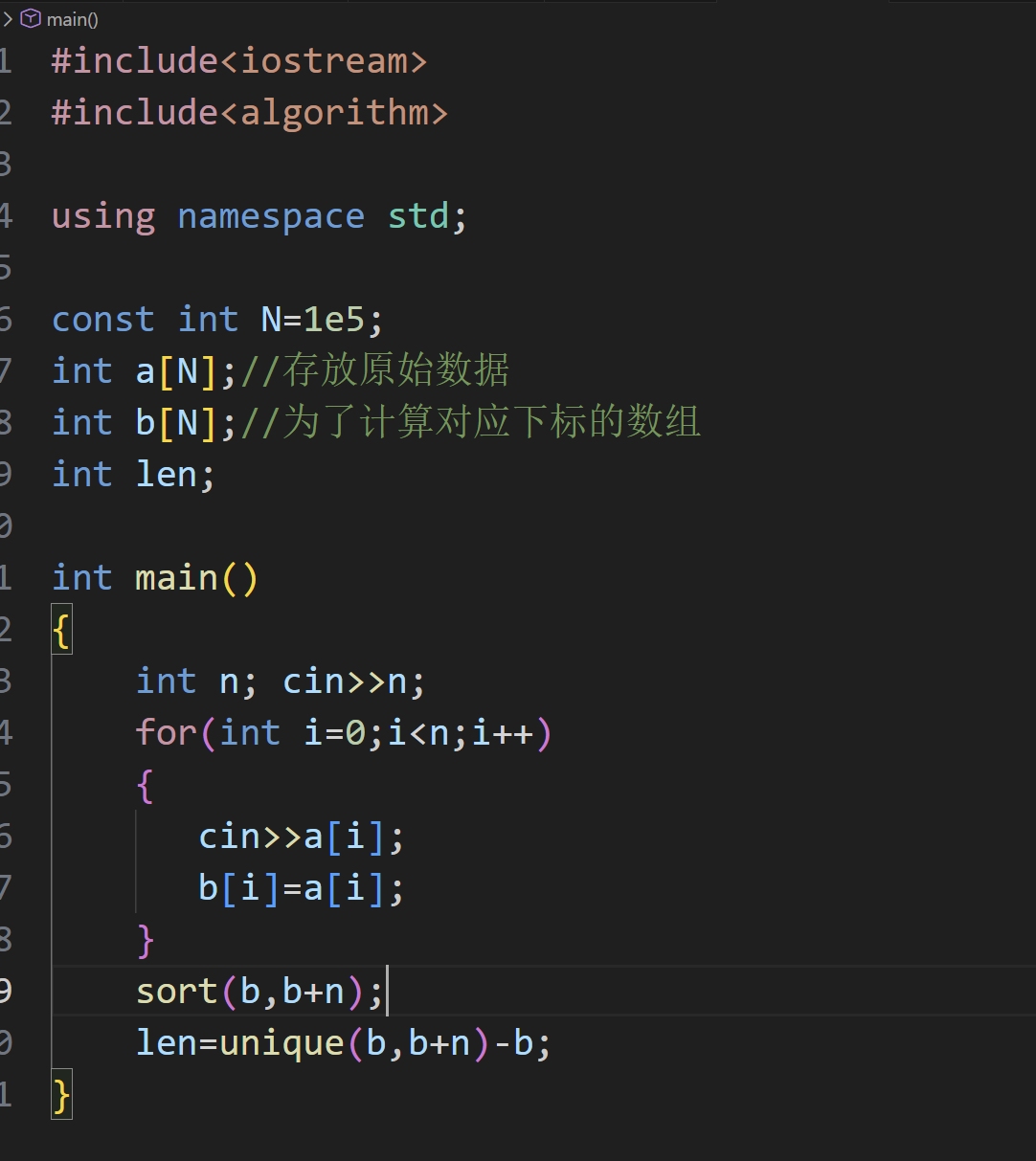
这里我们采用指针减指针的方式,求出去重后的 b 数组元素个数,接着就是用二分查找去找到目标值的位置,并返回下标,这样就完成了离散化对应较小数的执行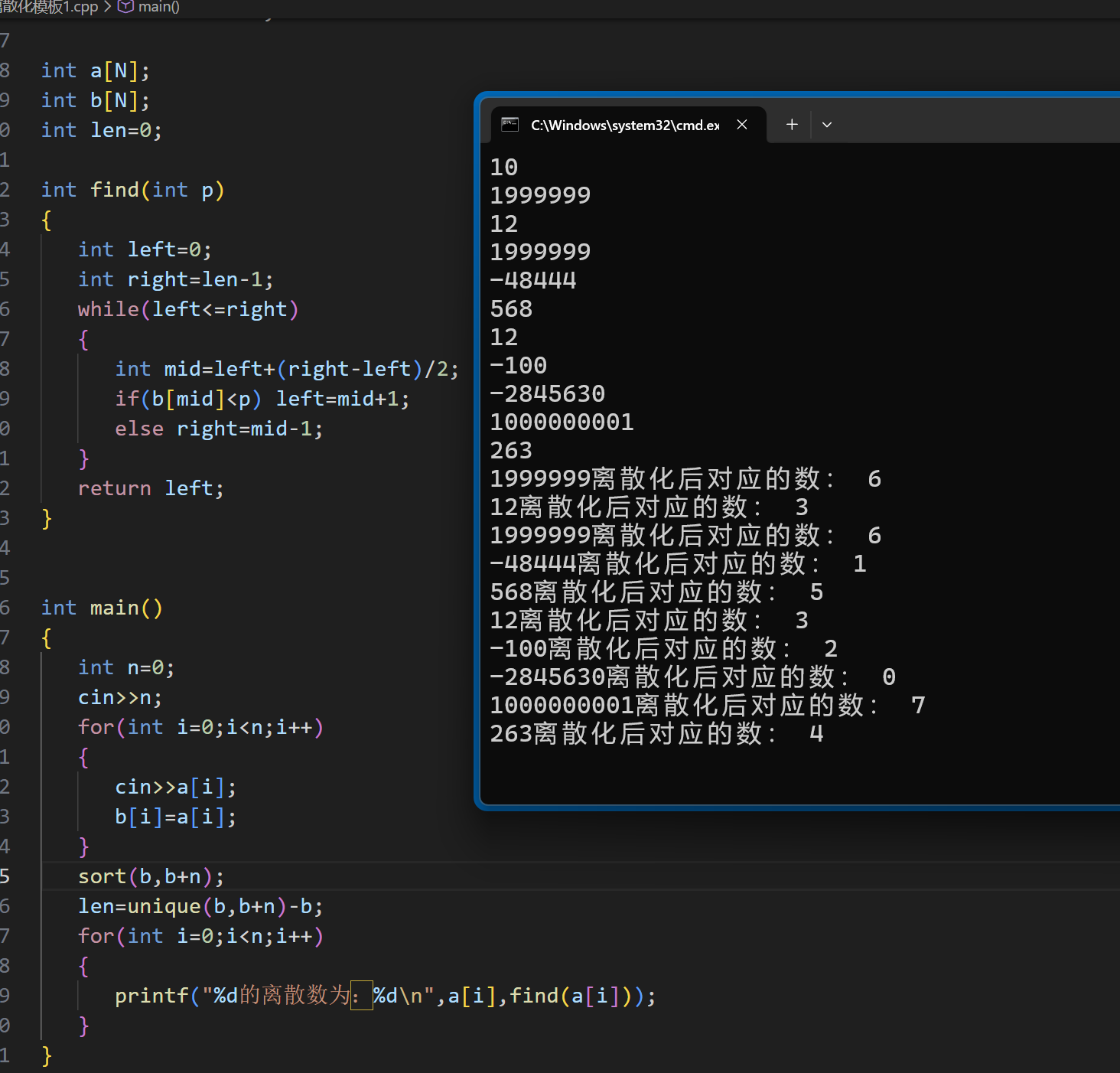
- 排序+借用哈希表去重和查找
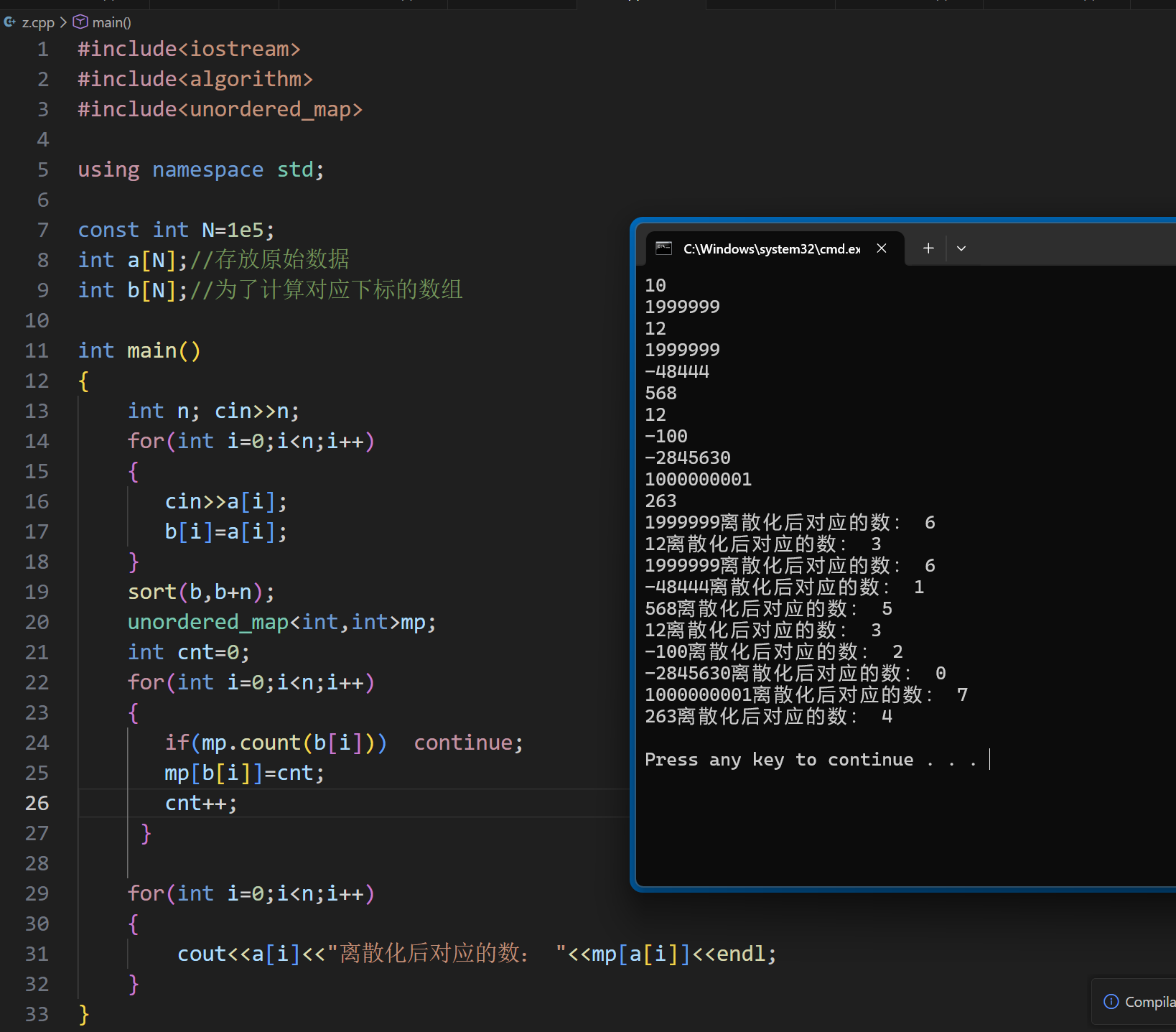
第24行的 if 语句的目的是去重,倘若检测到 b[ i ] 这个数对应的哈希值有值了,就要跳过这个数,接着就是向容器中按顺序放进去对应的 ”下标“
这是两种求离散化的模板,接下来来一道题目: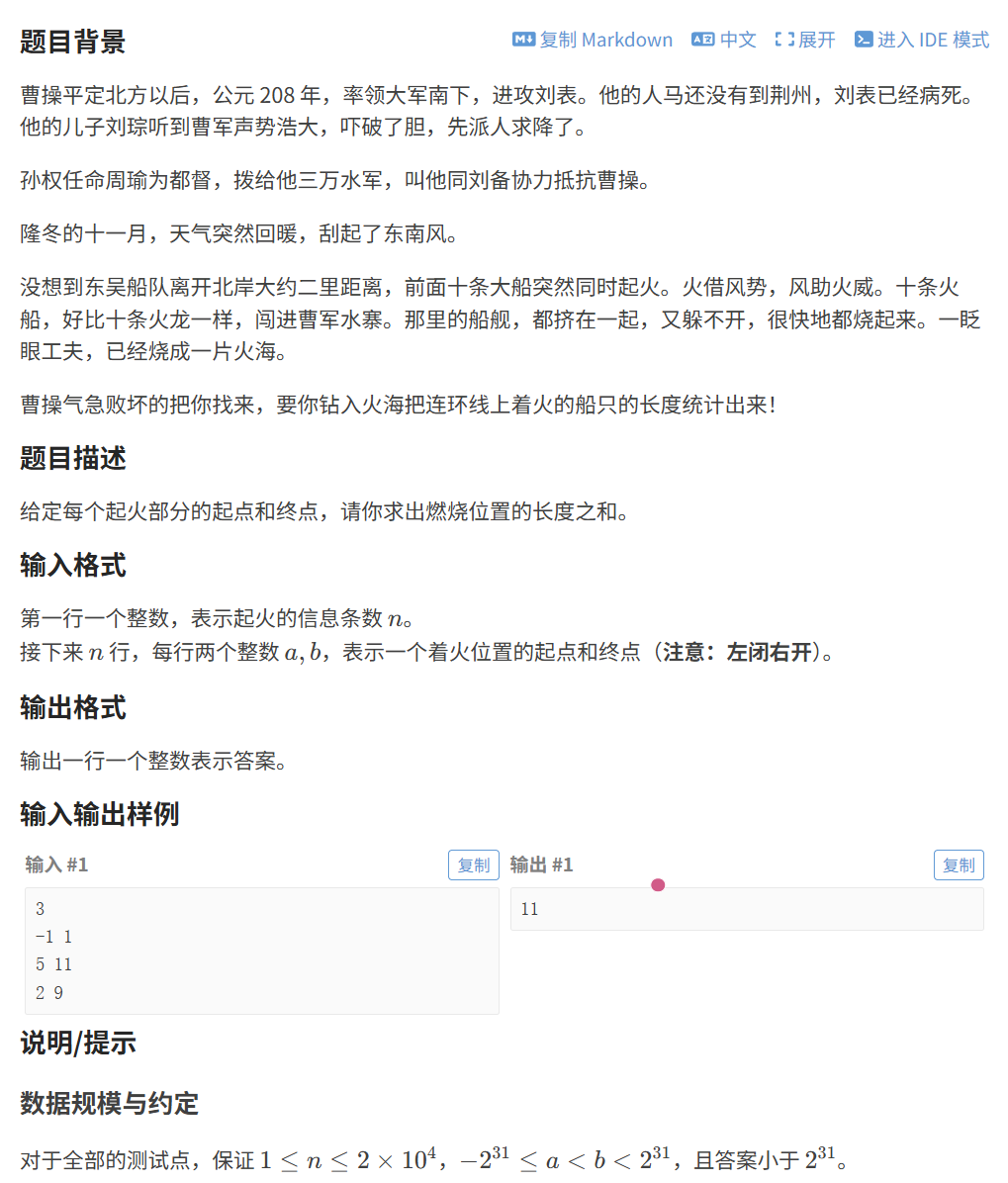
这个题可以看到,每一个区间的数很大,但是数据总量很小,这样就可以考虑离散化来处理素材,假定给一组数据:
3
1000 2000
1500 2500
3000 4000
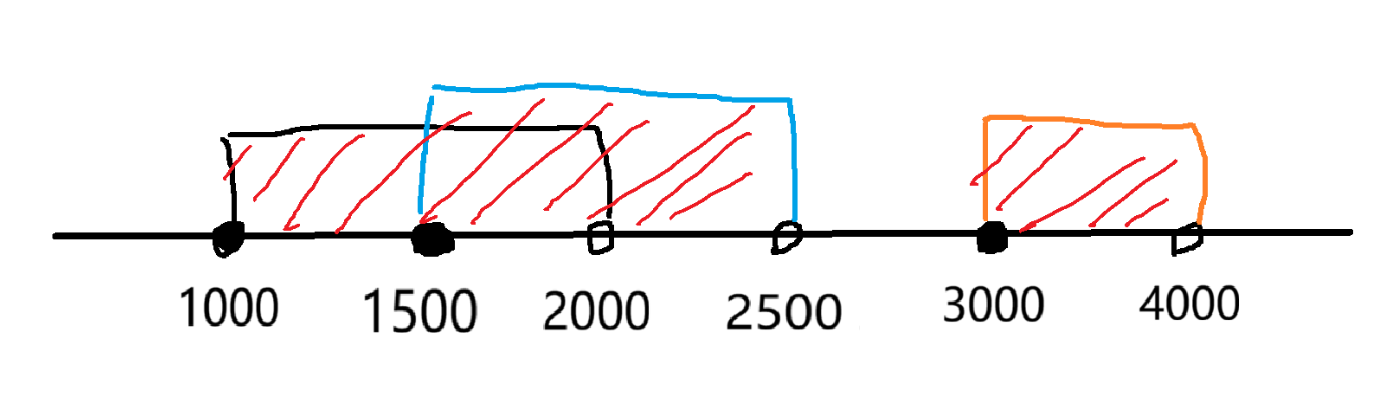
如上图,要求出船的总数量,就是红色阴影部分的长度,源于会有重复区间,我们允许考虑用差分,将每一段区间 +1 ,最后还原出数组,再统计出数组中数不为 0 的长度即可,但是直接用原始数据使用数组进行差分,下标会非常大,我们用离散化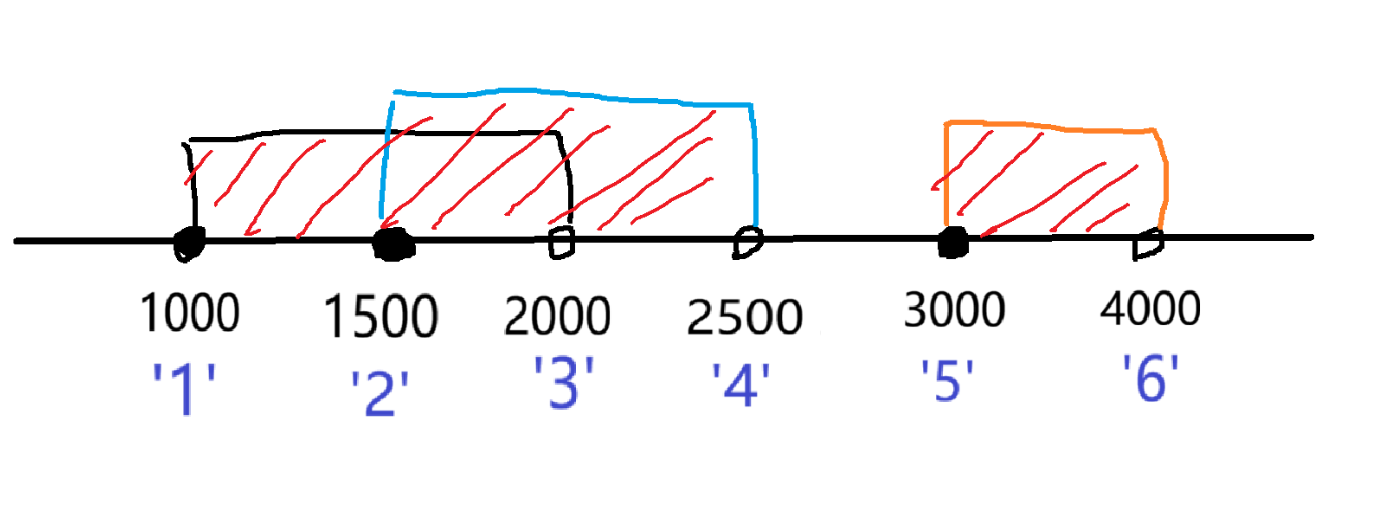
(因为要使用差分,这里起始下标记为 1 )
(为了很好区分离散化后所对应的数,我将数用单引号引起来)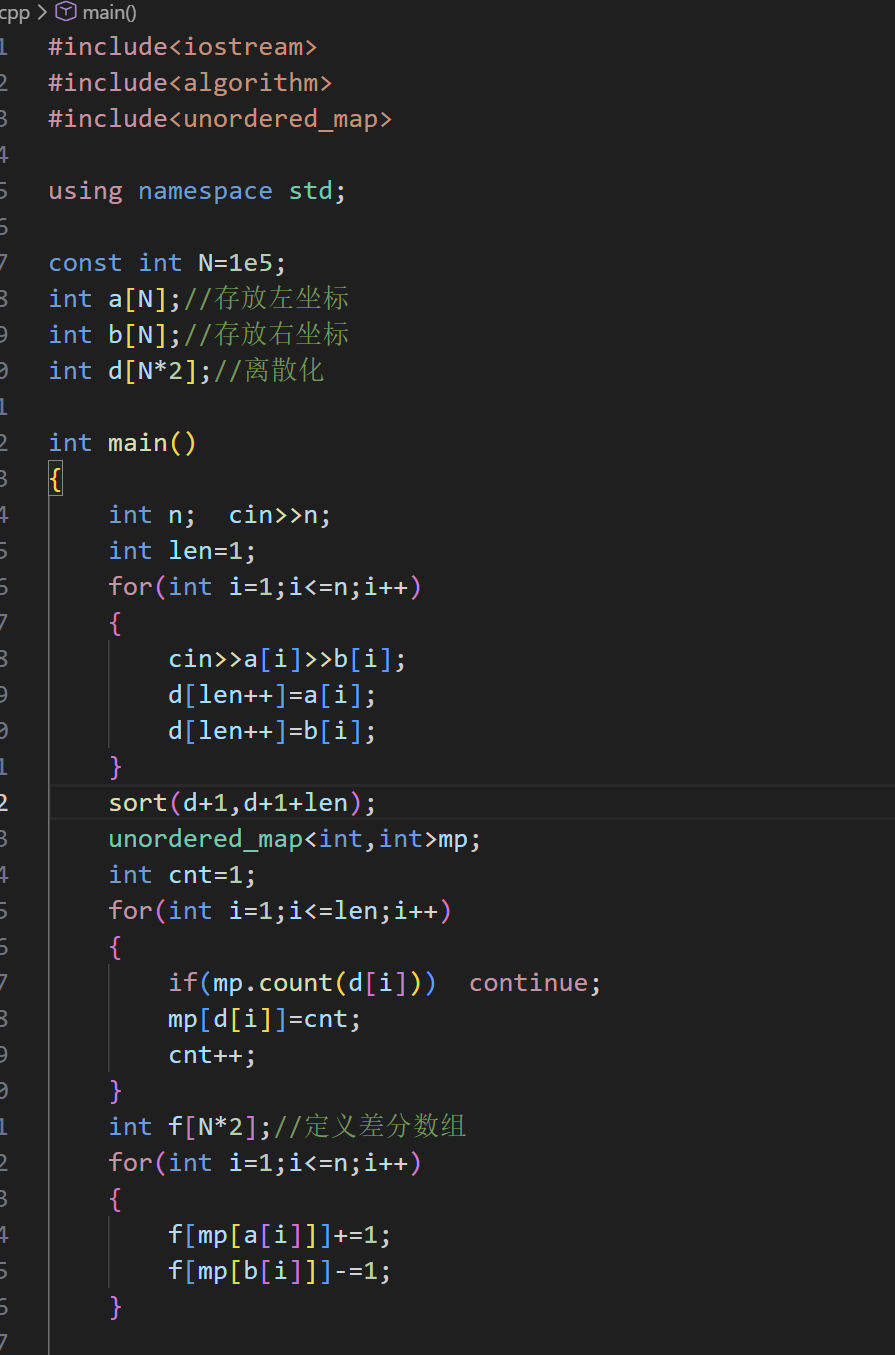
还原差分数组就是这样就完成了差分数组的创建,mp[a[i] ] 和 mp[b[i] ] 就是原素材对应的离散化后的”较小数“,接着就
还原差分数组后,就要来检查数组中 >0 的区间,并累加长度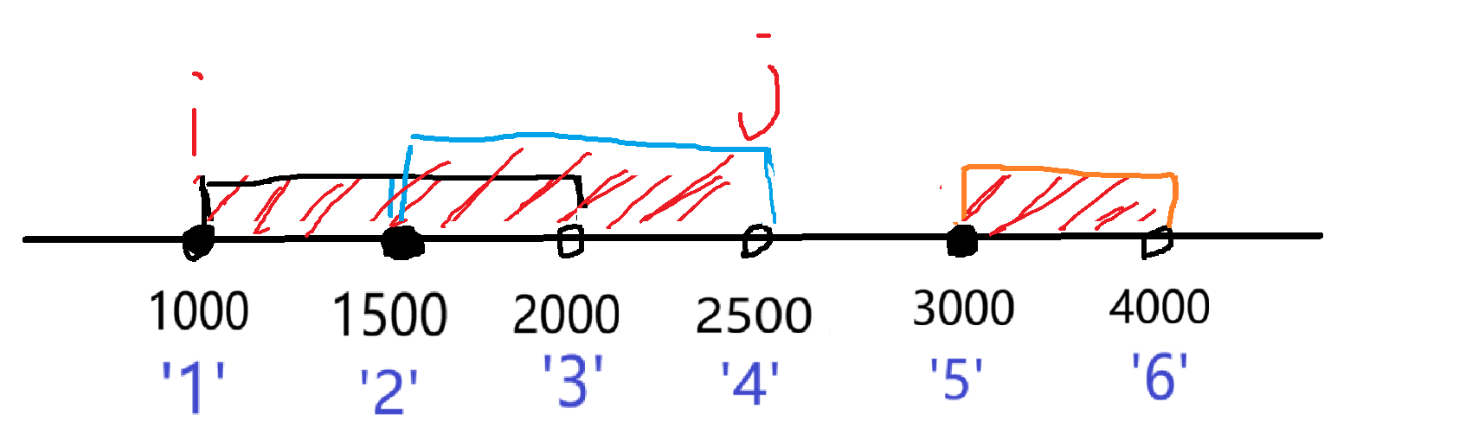
当找到 >0 区间的左右下标后,让 sum+= d [ j ] - d [ i ],注意这里用的是 d 数组( d 数组存的才是真实值!!)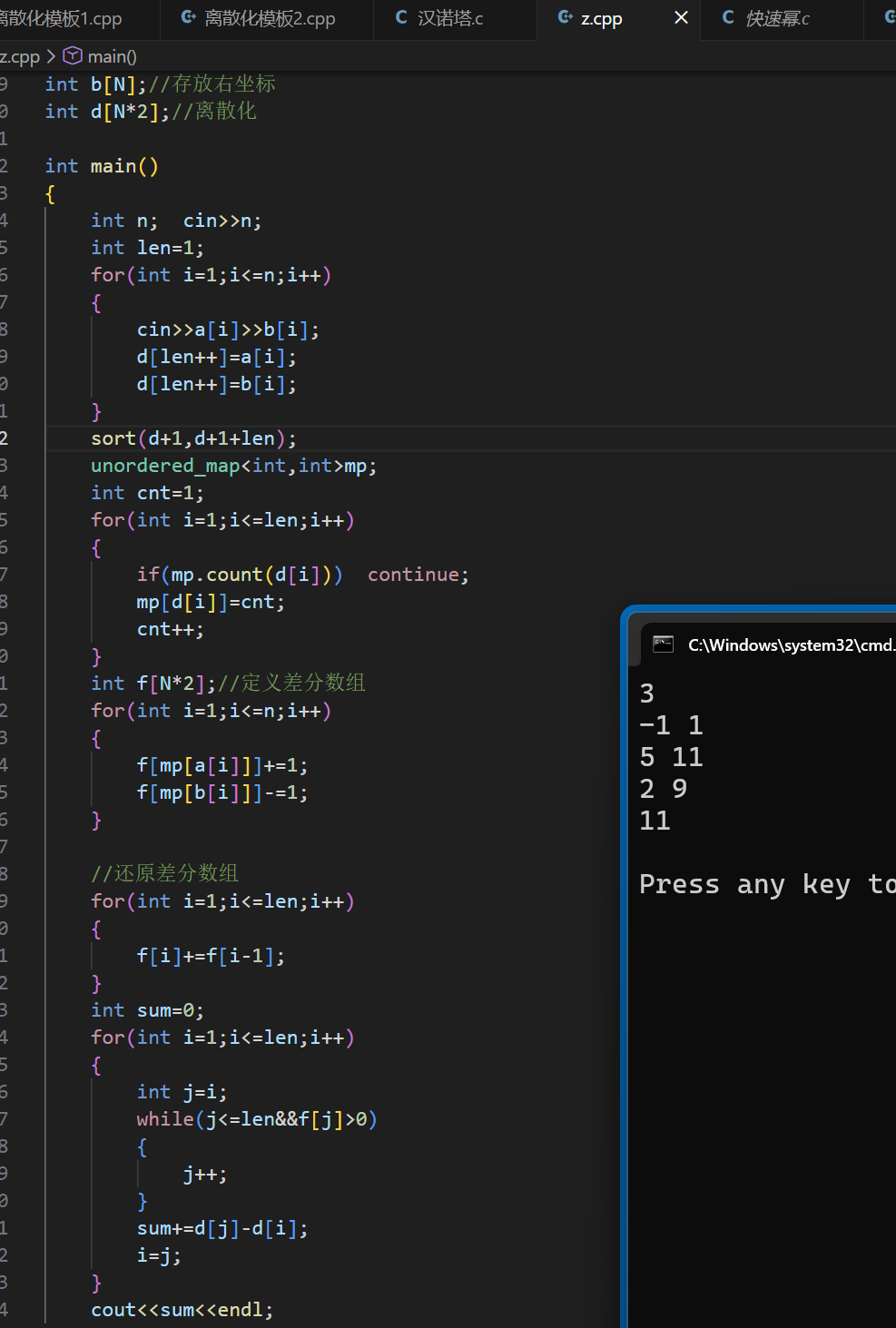
递归
在第 4 期的实战篇中我们已经了解过了递归思想,递归就是函数自己调用自己,这里我们要再深入学习一下:
大致分为3步走:
1.先找到相同的子疑问-----> 确定函数的作用以及函数的设计
如何解决的就是2.只关心某一个子问题
3.不能继续拆分的子问题------>递归出口(结束条件)
递归的本质:在处理主问题时,必须消除子问题,两者的处理方式完全一致
要注意的是:
1.递归一定要有终止条件,防止出现死递归
2.要以宏观思维来想,找到每一个子挑战相同的处理方式,函数只要求构建这个功能就行
先来看两个经典的计算题,这里我只给出结果:
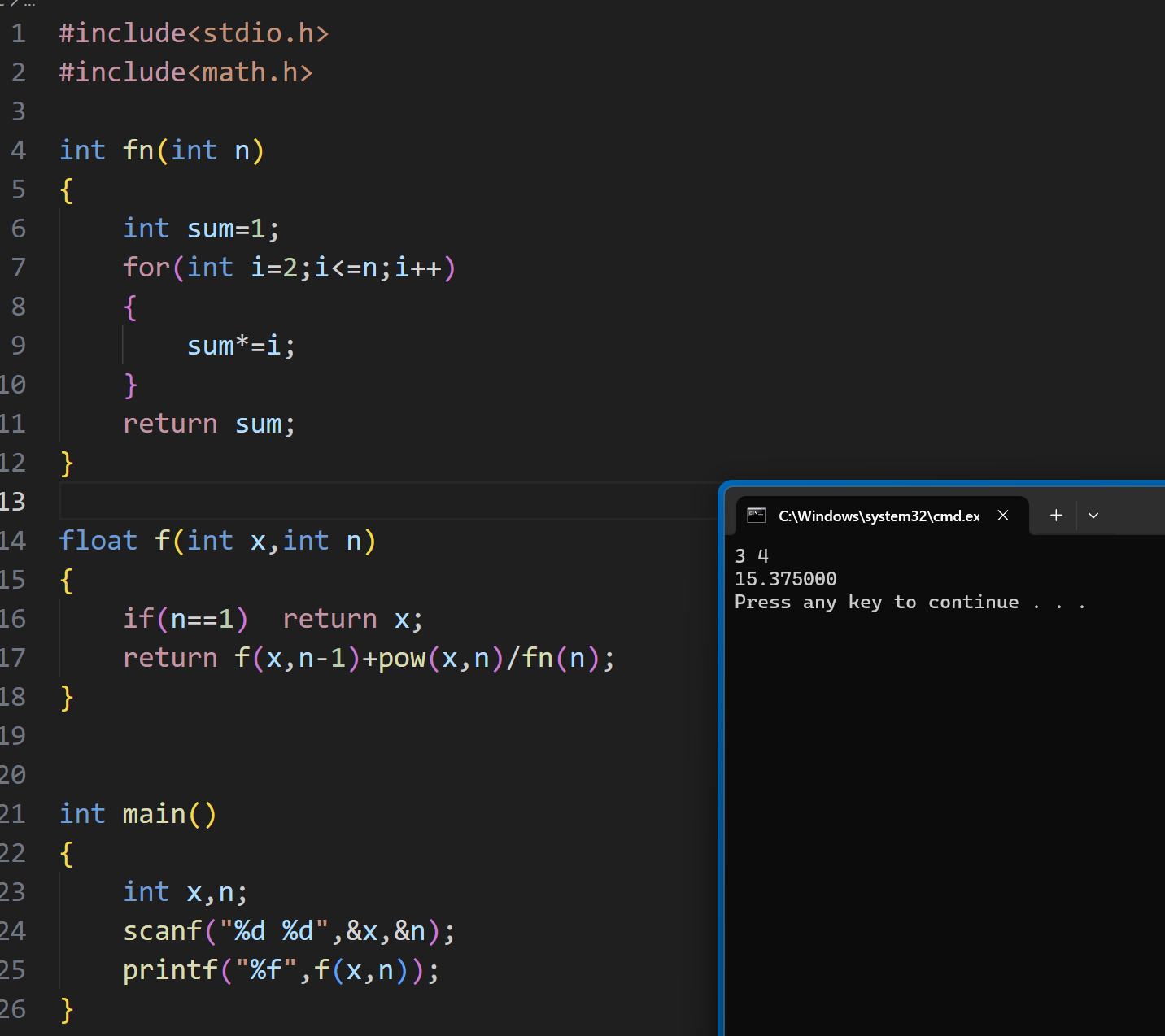
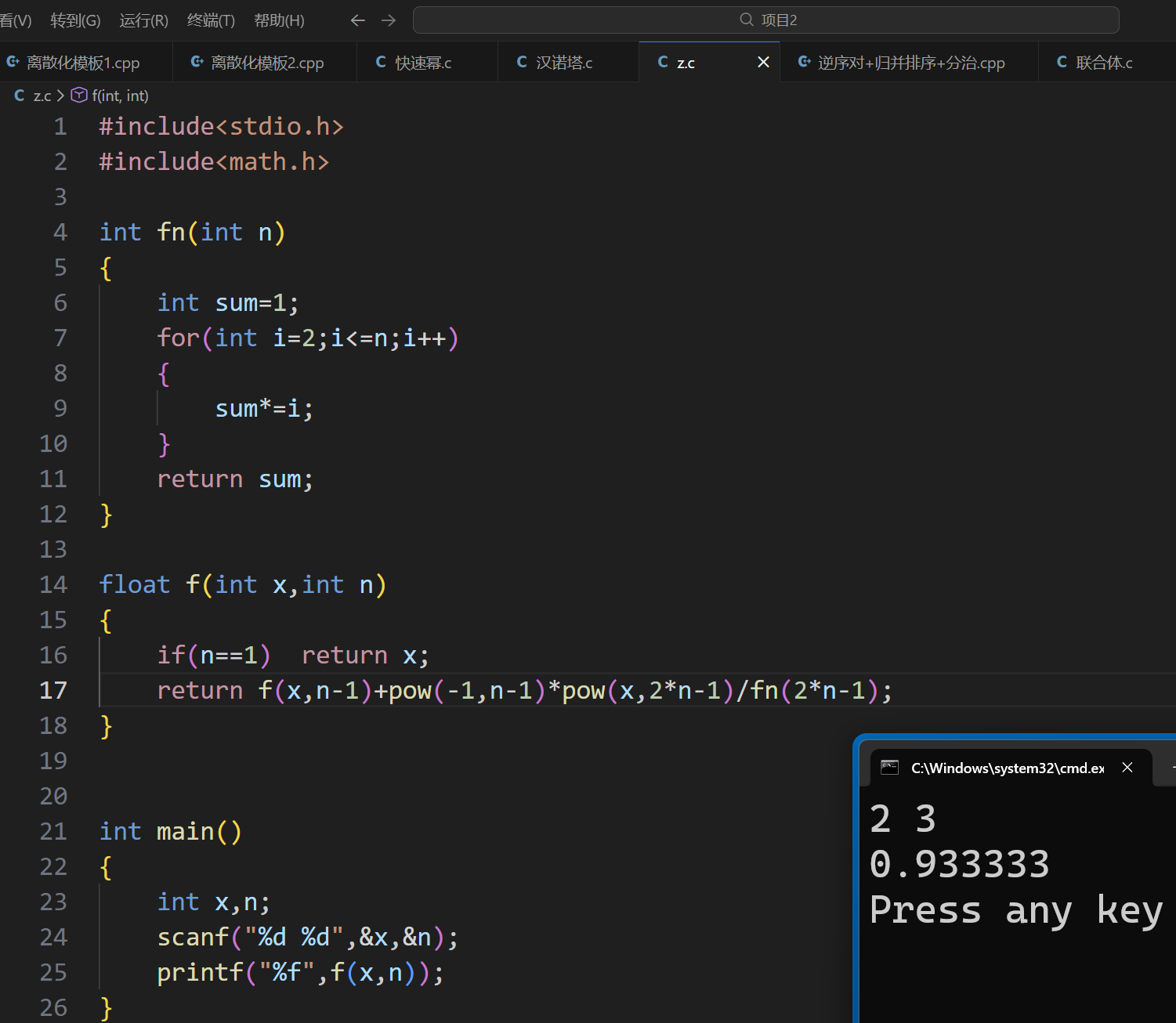
ok,现在正式开始进阶递归:
经典汉诺塔问题: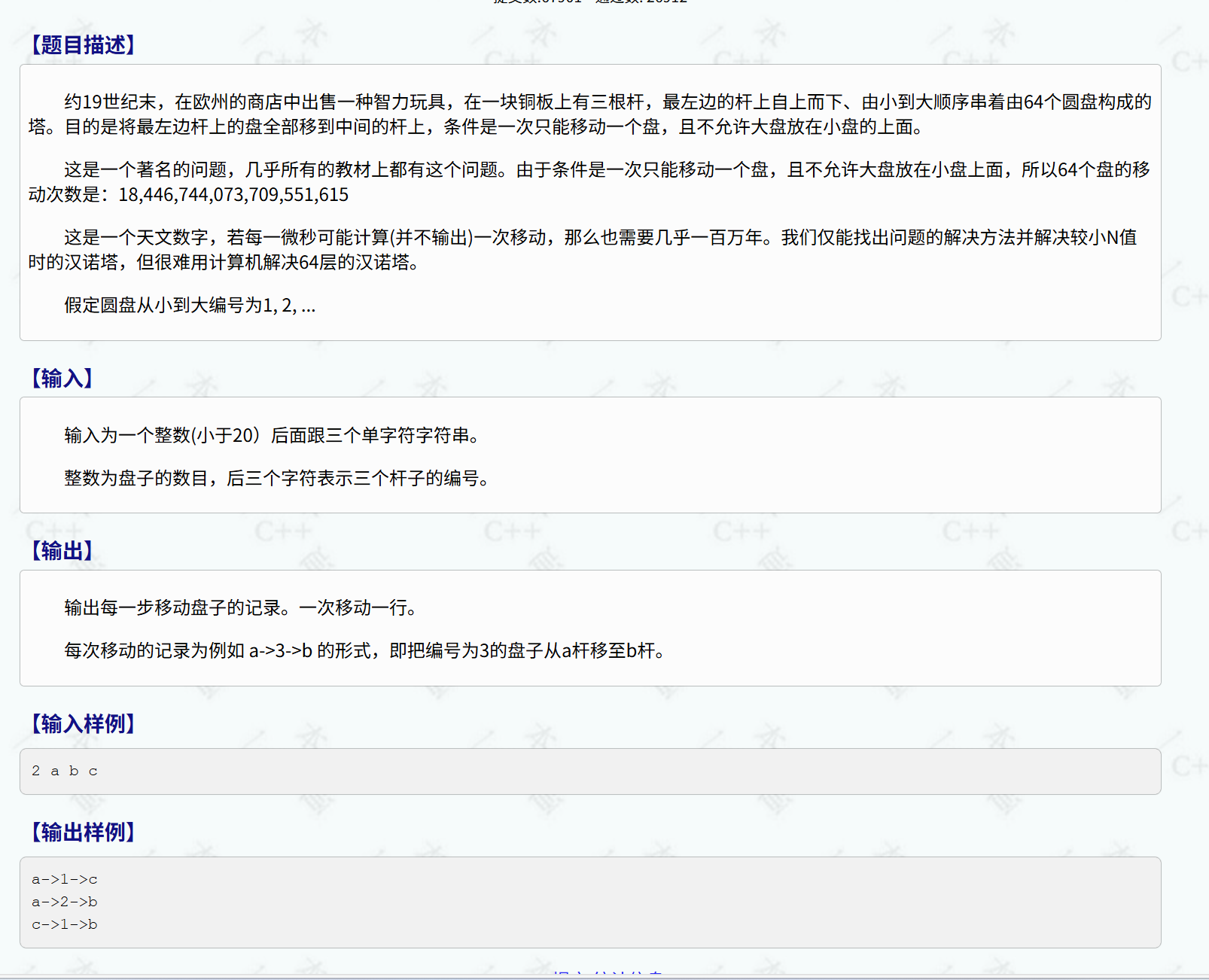
先来找一找能用相同处理方式解决的子难题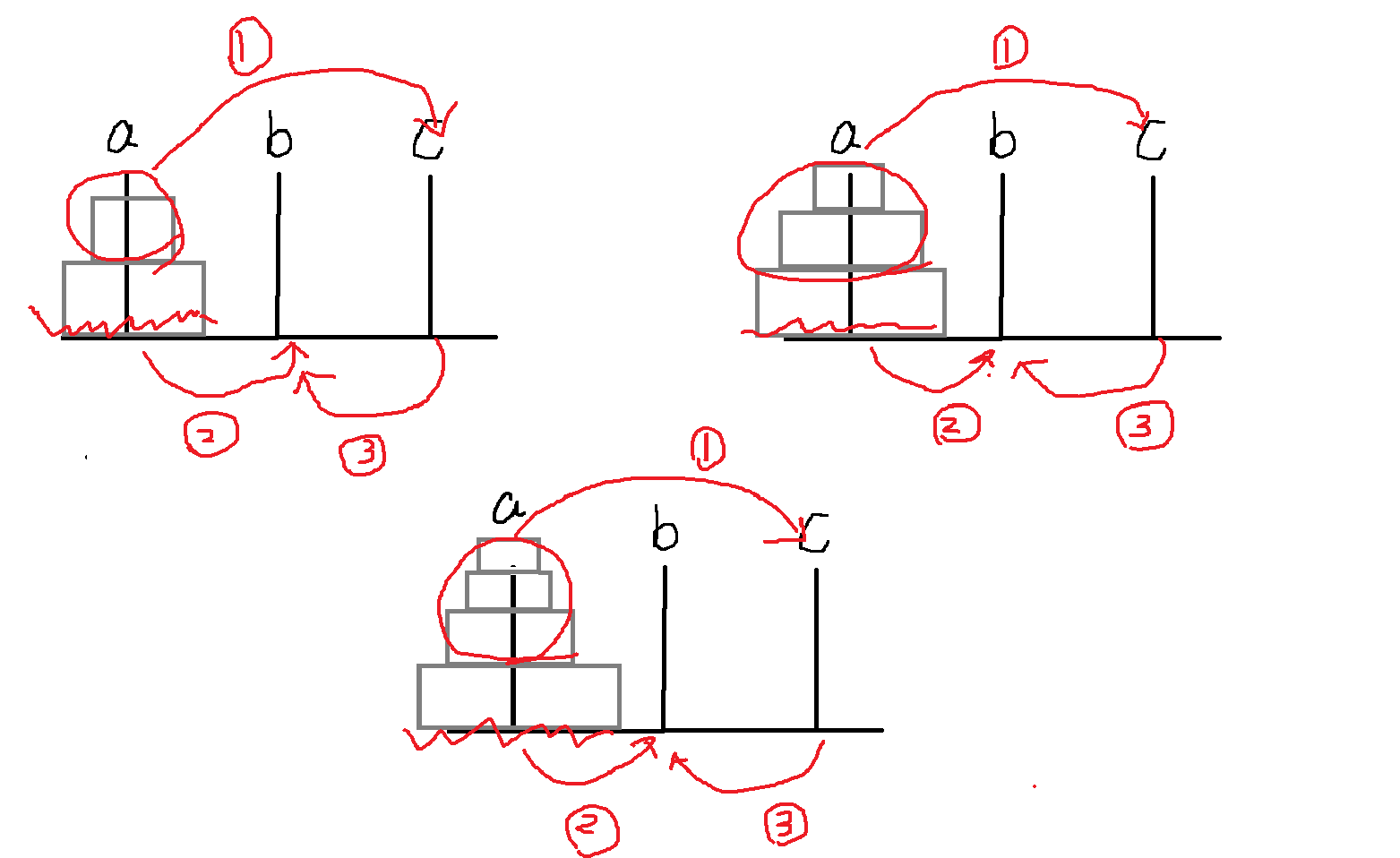
行看到不论一共有几个盘子,每一个的处理方式都是一样的,把 n-1 的盘子先转移到 c 柱上,再把最下的盘子放在目标柱 b 上,再把那 n-1 那一堆盘子放到 b 柱上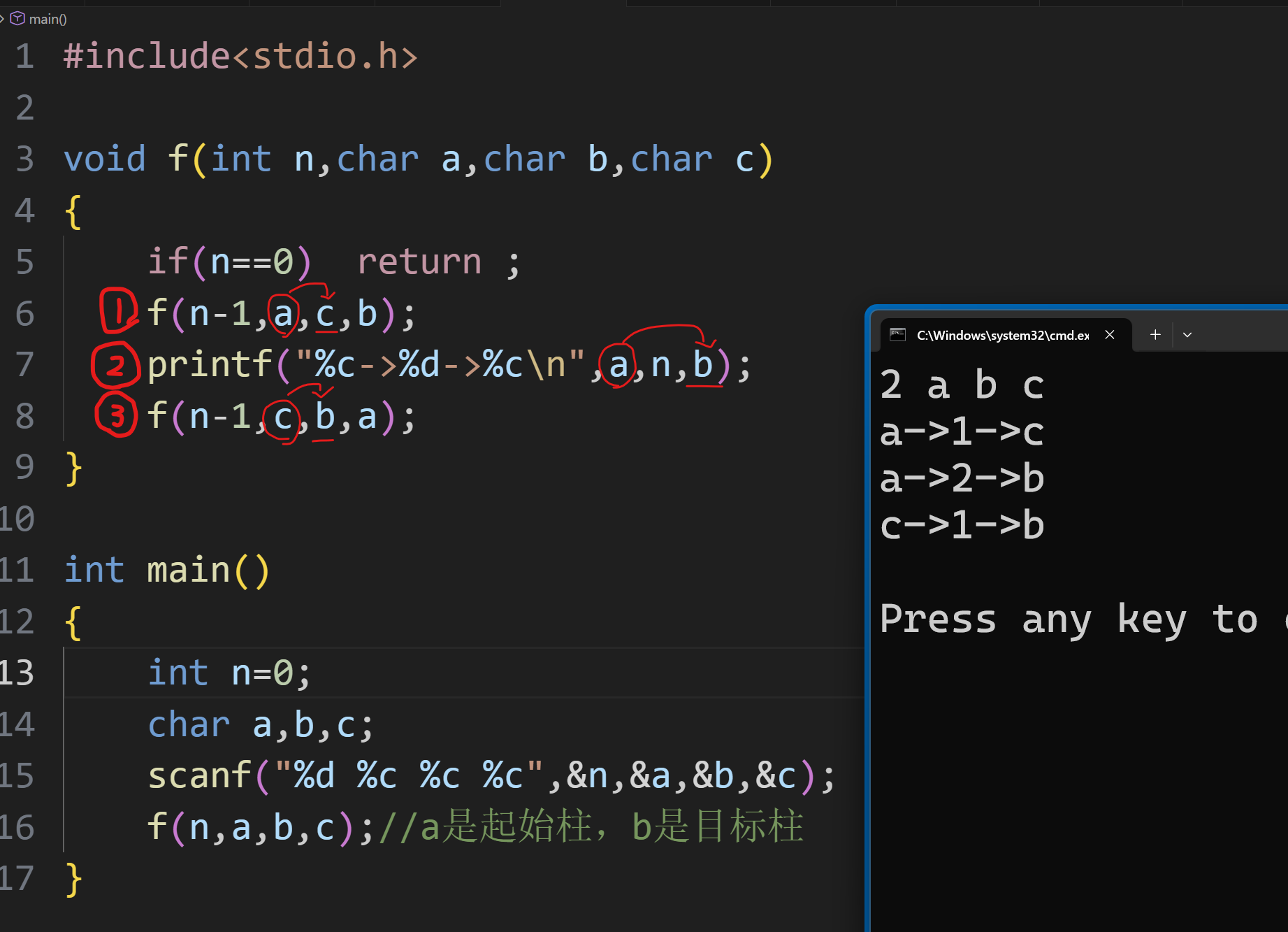
我们再来看一道题:
利用相同的处理方式,首先我们用数学解方程的方法求出每次分出来的两个节点 x,y就是这道题的每一次分群也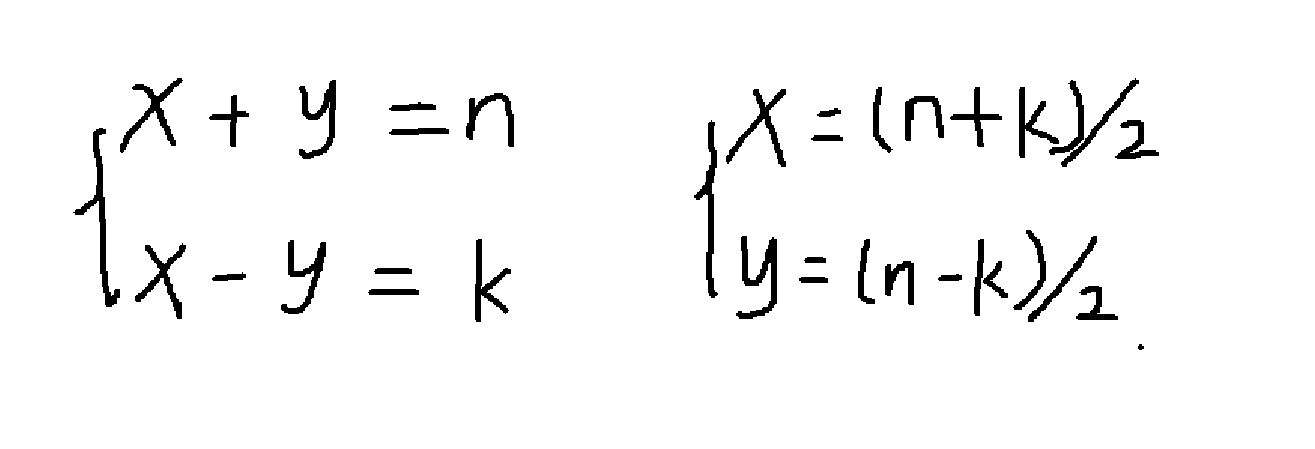
对于每一次的处理,要分为两个节点分别计算,如果节点不可再分的时候,就说明这一群牛就会安静吃草,记一次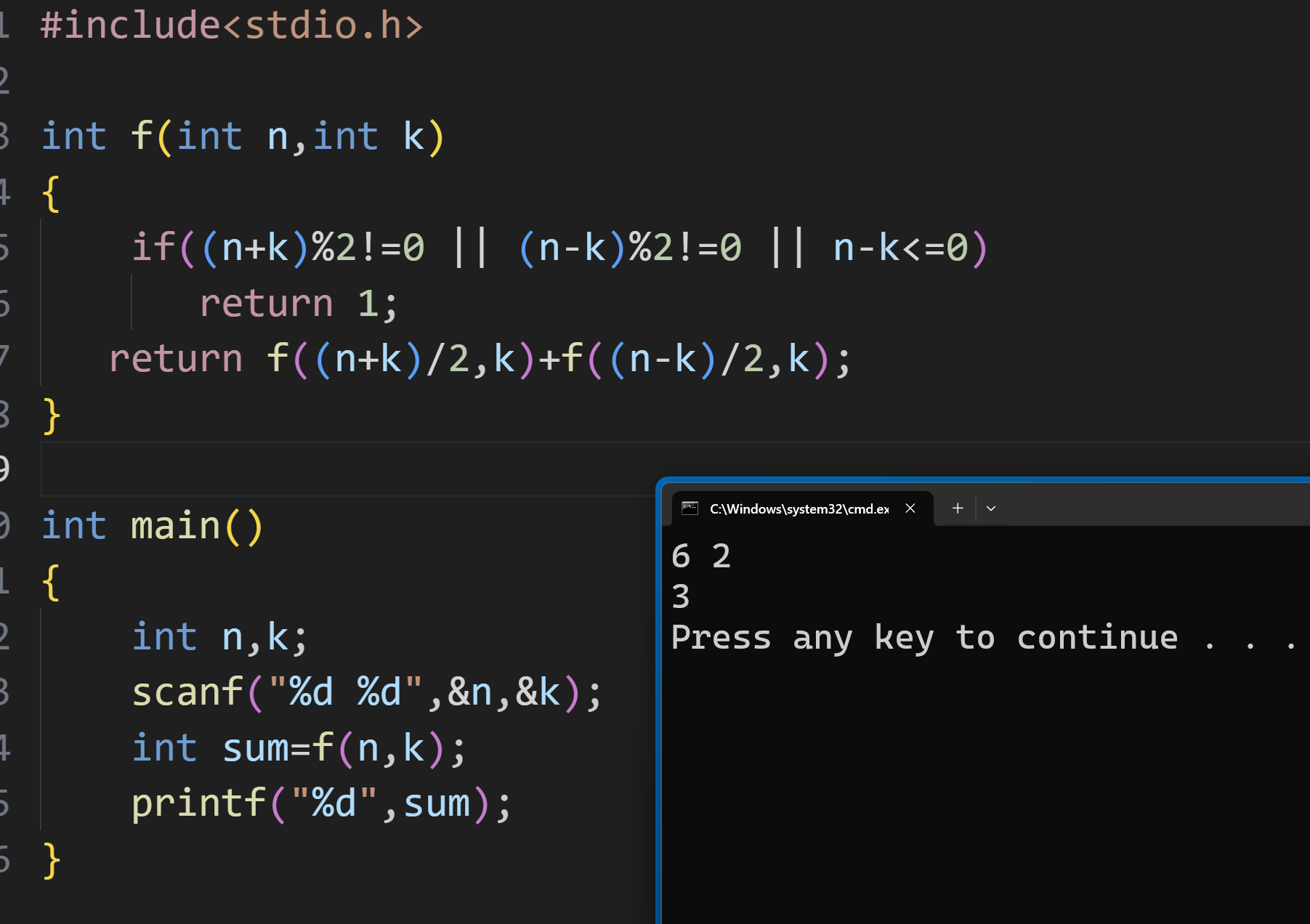
归并排序
分治是将大障碍拆解为多个独立的小的问题,然后去应对每一个小困难,解决每一个小问题以后,再将结果组合起来,最终解决原疑问
核心步骤分3步:
1.分解(拆):把大问题拆成结构相同、规模更小的子挑战(例如将数组拆成两个子数组)
2.解决(解);递归解决每个子障碍,直到子问题小到“无需再拆”(比如子数组只剩1个元素,天然有序)
3.合并(合);把所有子问题的解合并,得到原疑问的解
怎么实现的:就是我们来看看归并排序
因为每一个子问题都是相同的解决手段,就考虑用递归,具体看看相同的处理办法是怎么搞的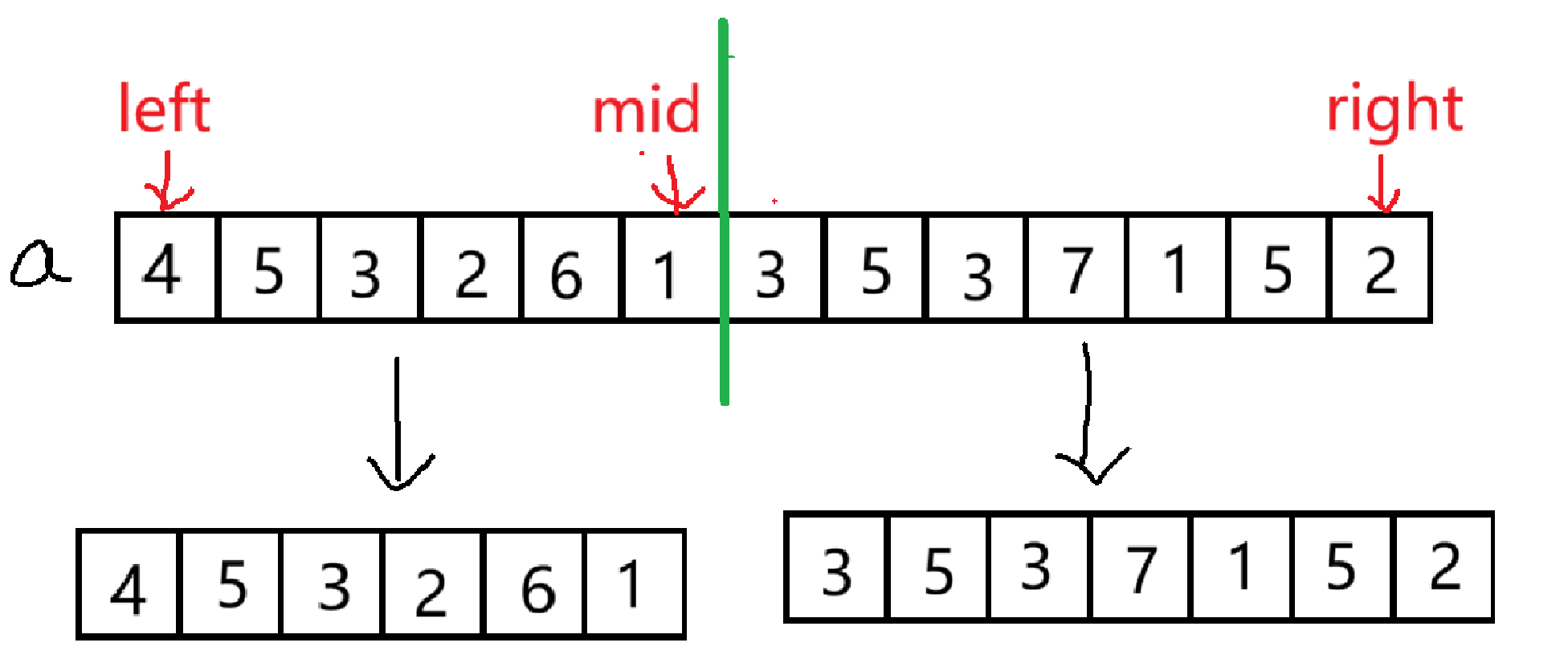
每个子数组分出来以后,将它们进入到函数中进行排序,这样返回的是有序的子数组
假设要将 a 数组中的数排序,先将数组的左右下标表示出来 left、right,寻找中间值mid,并将数组一分为二,要实现排序操作,就需要再定义一个数组 b 来存储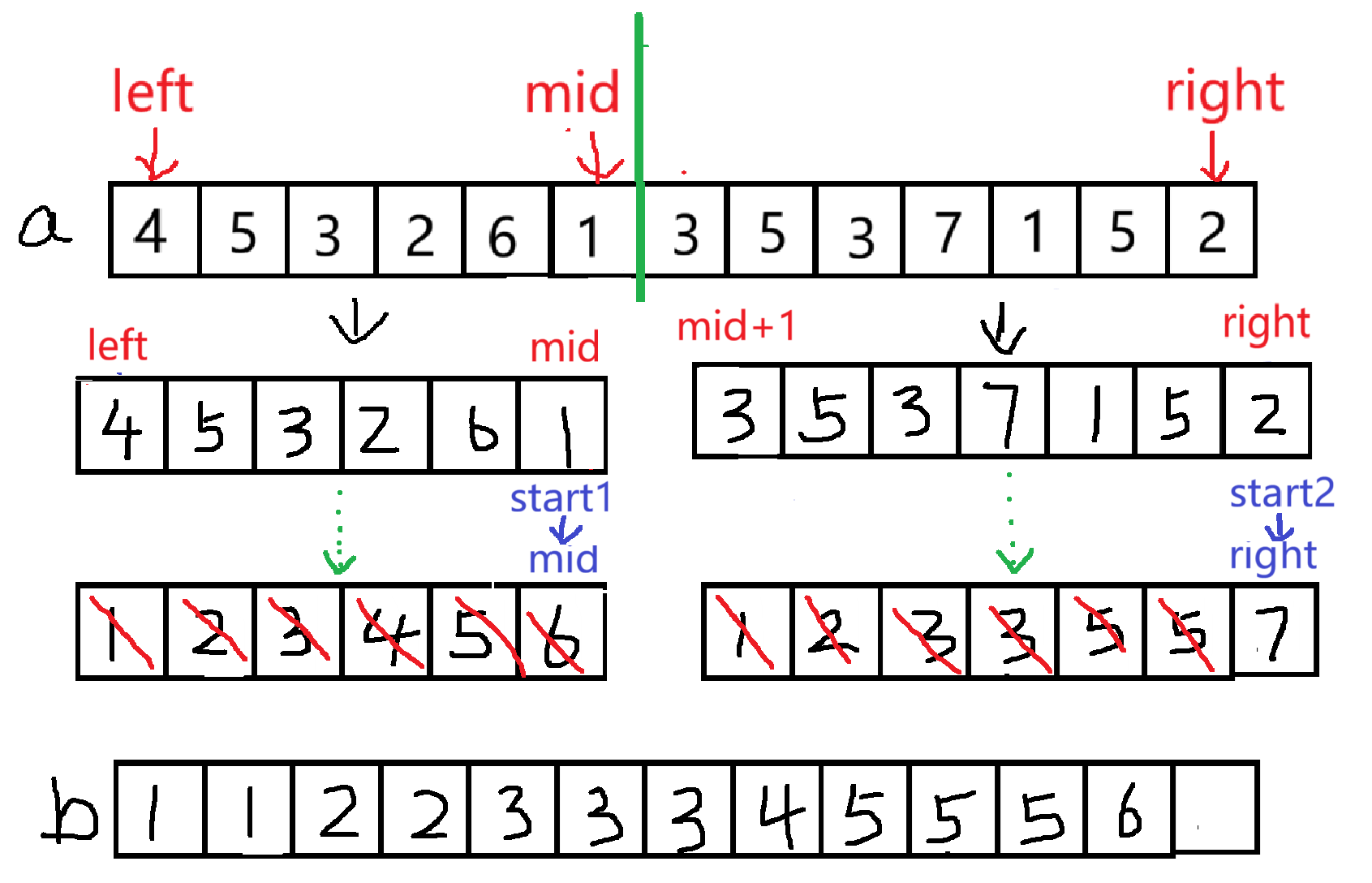
比较分出来的两个数组,每次将较小的值放在 b 数组中,当 start1 和 start2 其中一个到了边界时,就要把还有剩余元素的数组中的数放进数组 b 中,并且将 a 的数顺序更新为 b ,由此递归的返回条件是:当 left>=right 时,这时候就不能再分成两个数组了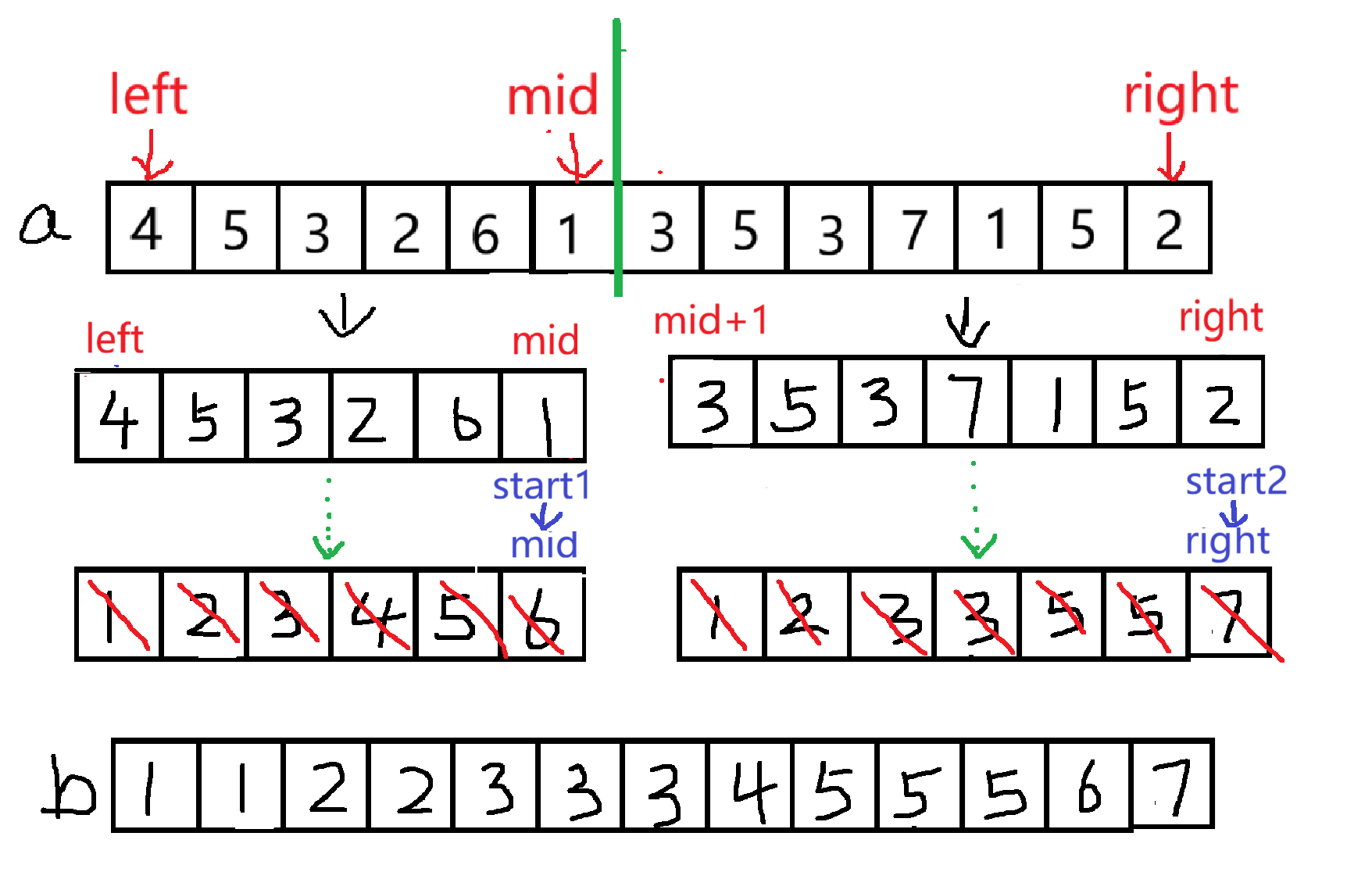
这里展示主函数代码:
我们来看看分治思想+归并排序来解除实际问题:
这个题要求出一个数组中逆序对的个数,借助归并排序的思路,想想我们的递归函数要达成什么功能?
在每一次的分数组中,逆序对由三个部分组成,一个是左子数组内部的逆序对个数,一个是右子数组内部的逆序对数,另一个是跨左右子数组的逆序对
每一次完成递归函数时,返回的就是每一个子数组内部的逆序对数,并且子数组已经被排序,接着大家只需要求出跨左右子数组的逆序对就行
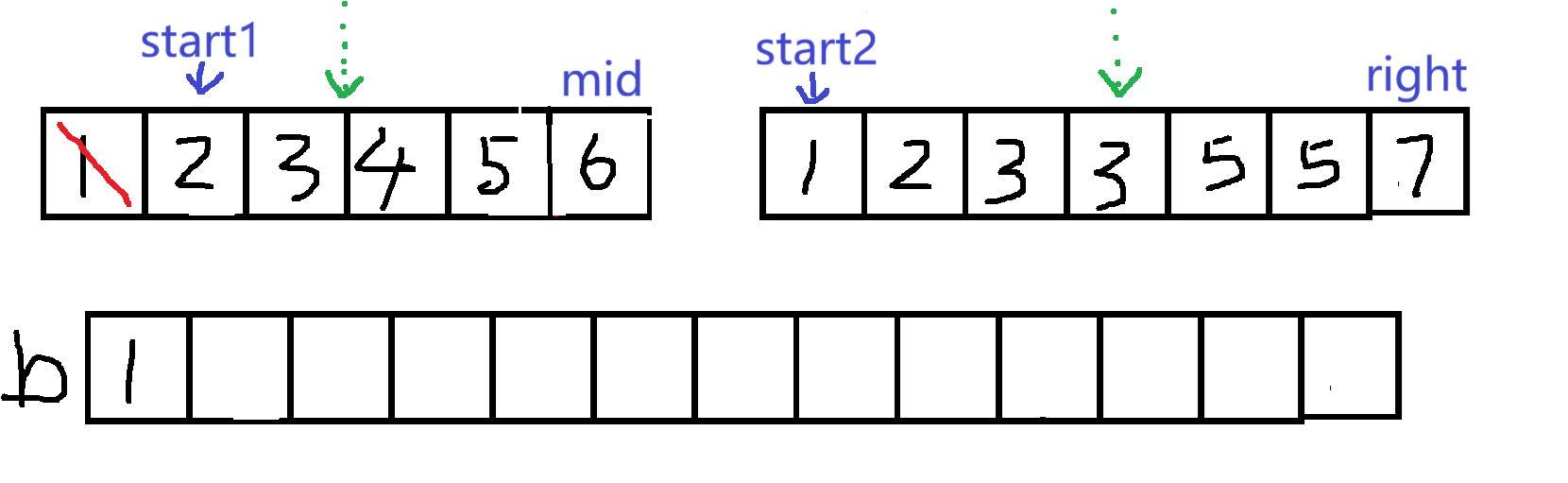
有序数组)就说明start1~mid 之间的数都要大于start2 所指向的数就是当 start1 指向的数大于 start2 指向的数时,(源于
根据上面的分析,可能看出来就是归并排序多了一步------计算逆序对
代码实现: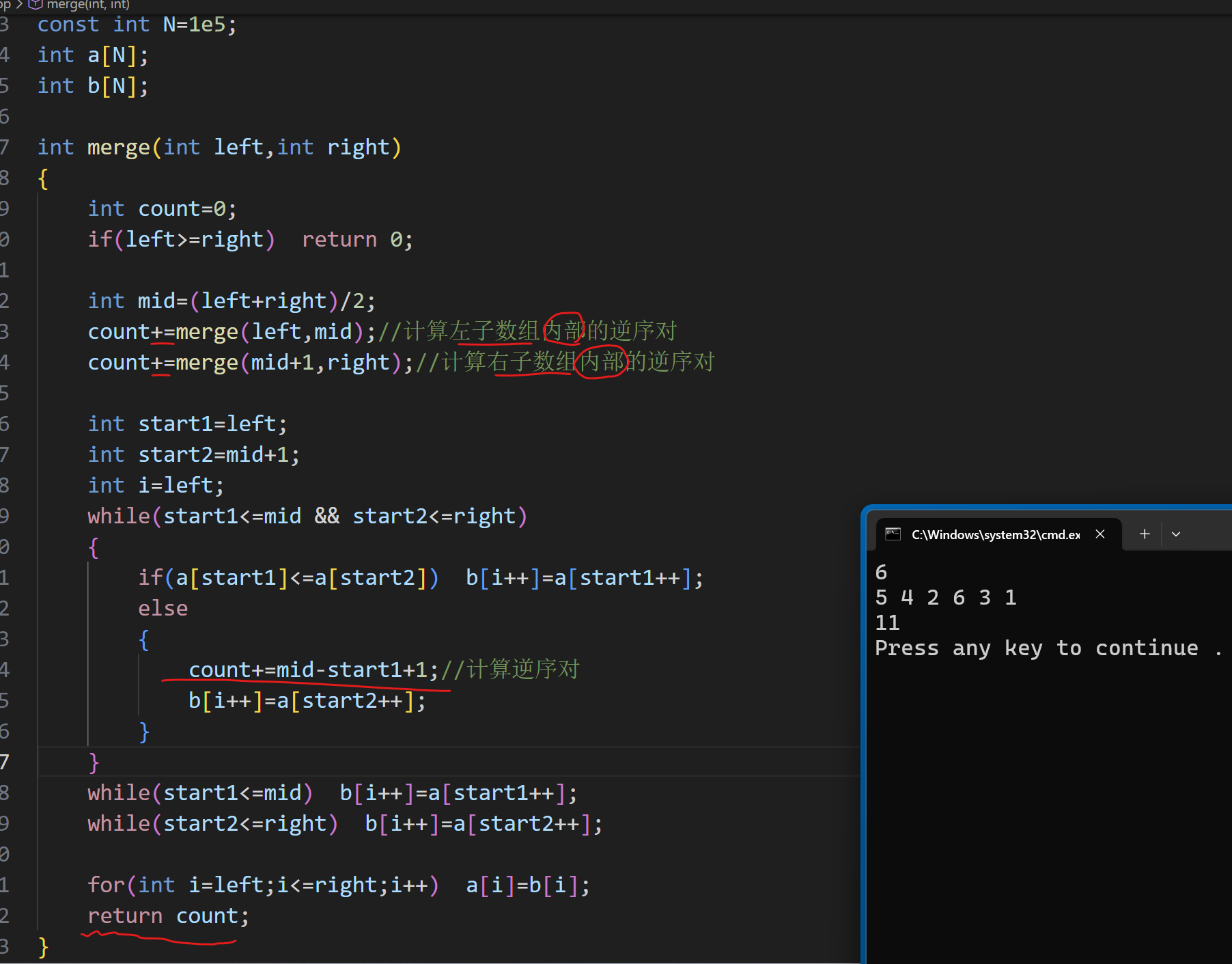
结语:
好了,终于是完成了这一期的算法实战篇,总的思维量还是很大的,大家行收藏以后慢慢消化理解,制作不易,感谢您的观看与支持




 浙公网安备 33010602011771号
浙公网安备 33010602011771号