HDLBits 刷题分享 Shift Registers Verilog零基础刷题教程
系列导航:上一章 | 目录 | 下一章
⏱️ 阅读时间:30分钟 | 难度:★★★☆☆ | ✅ 完成度:9/9题本文档特色:
- ✅ 完全正确的答案代码:所有代码都经过验证,确保在HDLBits平台通过
- ✅ 深度逻辑解析:每个重要代码段都有详细的"为什么这么写"的解释
- ✅ 硬件思维培养:从硬件电路角度解释Verilog代码的实现原理
- ✅ 实践导向:结合DE1-SoC等实际开发板的应用场景
本章概览
学习目标
完成本章后,你将掌握:
- ✅ 移位寄存器的基本原理与实现方法
- ✅ 循环移位与算术移位的区别
- ✅ 线性反馈移位寄存器(LFSR)的设计与应用
- ✅ 位拼接与移位操作符的高级用法
知识图谱
题目清单
| 题目 | 难度 | 核心考点 | 预计时间 |
|---|---|---|---|
| 4-bit shift register | ★★☆ | 基础移位、case语句 | 15min |
| Left/right rotator | ★★☆ | 循环移位、方向控制 | 15min |
| Left/right arithmetic shift | ★★★ | 算术移位、符号扩展 | 20min |
| 5-bit LFSR | ★★★ | 线性反馈、伪随机数 | 20min |
| 3-bit LFSR | ★★☆ | LFSR基础、多项式 | 15min |
| 32-bit LFSR | ★★★ | 标准LFSR、大位宽 | 20min |
| Shift register1 | ★☆☆ | 串行输入、简单移位 | 10min |
| Shift register2 | ★★☆ | 参数化设计、多功能 | 15min |
| 3-input LUT | ★★★ | 查找表、FPGA基础 | 20min |
题目1:4-bit shift register
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Shift4
- 标签:
#移位寄存器#异步复位#优先级控制 - 难度:★★☆☆☆
题目分析
输入输出
module top_module(
input clk,
input areset, // 异步高电平复位
input load, // 同步加载信号
input ena, // 使能信号
input [3:0] data, // 并行输入数据
output reg [3:0] q // 移位寄存器输出
);功能需求
实现一个4位右移移位寄存器,具有以下功能:
areset: 异步复位到0load: 并行加载data[3:0]ena: 使能右移(高位补0,低位移出)- 优先级:
load > ena
测试用例
| areset | load | ena | data | q初始 | q结果 | 说明 |
|---|---|---|---|---|---|---|
| 1 | x | x | x | xxxx | 0000 | 异步复位 |
| 0 | 1 | x | 1010 | xxxx | 1010 | 加载数据 |
| 0 | 0 | 1 | x | 1010 | 0101 | 右移一位 |
| 0 | 1 | 1 | 1100 | 1010 | 1100 | load优先 |
核心知识点
知识点1:移位操作符
定义:Verilog提供<<(左移)和>>(右移)操作符
语法:
// 逻辑移位(补0)
q <= q >> 1; // 右移1位: [3:0] -> [0,3:1]
q <= q << 1; // 左移1位: [3:0] -> [2:0,0]
// 算术移位(保留符号位)
q <= q >>> 1; // 算术右移常见误区 ⚠️
// ❌ 错误:移位会改变位宽
wire [3:0] a = 4'b1010;
wire [3:0] b = a >> 1; // b = 4'b0101 ✓
// ❌ 错误:符号扩展混淆
reg signed [3:0] c = 4'b1010; // -6
wire [3:0] d = c >>> 1; // 1101 (-3) ✓
wire [3:0] e = c >> 1; // 0101 (5) 逻辑移位知识点2:异步复位 vs 同步复位
区别:
// 异步复位(areset出现立即复位)
always @(posedge clk or posedge areset) begin
if (areset)
q <= 0;
else
// 正常逻辑
end
// 同步复位(等待时钟边沿)
always @(posedge clk) begin
if (reset)
q <= 0;
else
// 正常逻辑
end知识点3:优先级编码
使用if-else实现优先级:
if (highest_priority)
// 操作1
else if (medium_priority)
// 操作2
else if (lowest_priority)
// 操作3
else
// 默认操作️ 解题思路
第一步:理解移位过程
初始: q = [q3, q2, q1, q0]
右移: q = [0, q3, q2, q1] // q0移出并丢失第二步:确定优先级
areset (最高) > load > ena > 保持第三步:代码实现
module top_module(
input clk,
input areset,
input load,
input ena,
input [3:0] data,
output reg [3:0] q
);
// 方案1:标准写法
always @(posedge clk or posedge areset) begin
if (areset)
q <= 4'b0;
else if (load)
q <= data;
else if (ena)
q <= q >> 1; // 右移操作
// else隐含:q <= q (保持)
end
/* ========== 代码逻辑深度解析 ==========
*
* 1. 为什么用异步复位?
* 异步复位(areset)优先级最高,因为复位信号是紧急情况下的安全措施。
* 不需要等待时钟边沿,一旦areset=1就立即执行复位,确保系统快速回到安全状态。
*
* 2. 为什么敏感列表包含"posedge areset"?
* 这就是异步复位的关键!敏感列表中的任何信号变化都会触发always块执行。
* 如果只有"posedge clk",那就是同步复位,需要等待时钟上升沿才能复位。
*
* 3. 为什么优先级是 areset > load > ena?
* 这是硬件设计的优先级逻辑:
* - areset:最高优先级,安全第一
* - load:中等优先级,加载新数据比移位更重要
* - ena:最低优先级,正常的数据移动操作
*
* 4. 为什么用"q <= q >> 1"而不是其他写法?
* "q >> 1"是Verilog的算术操作符,硬件综合后会直接生成移位器电路。
* 等价写法:"{1'b0, q[3:1]}",但操作符更简洁清晰。
*
* 5. 为什么不需要"else q <= q"?
* 因为reg变量默认保持值。当时钟到来但没有任何条件满足时,
* q会自动保持之前的值,这正好符合寄存器的"保持"特性。
*/
// 方案2:使用三目运算符(不推荐,可读性差)
// always @(posedge clk or posedge areset) begin
// q <= areset ? 4'b0 : (load ? data : (ena ? q>>1 : q));
// end
endmoduleSubmit状态: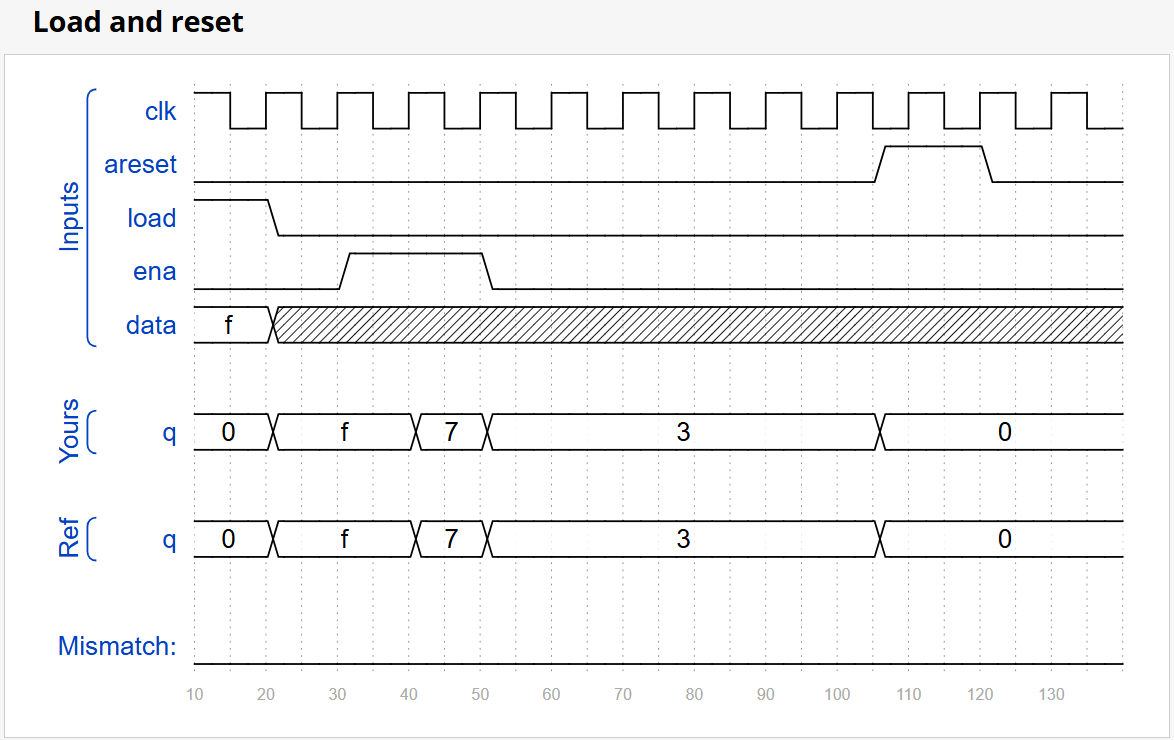
⚠️ 易错点总结
- 忘记异步复位的敏感列表
- 错误:
always @(posedge clk) - 正确:
always @(posedge clk or posedge areset)
- 错误:
- 优先级顺序错误
- 如果
load和ena同时为1,必须执行load
- 如果
- 移位方向混淆
- 右移:
q >> 1等价于{1'b0, q[3:1]} - 左移:
q << 1等价于{q[2:0], 1'b0}
- 右移:
题目2:Left/right rotator
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Rotate100
- 标签:
#循环移位#位拼接 - 难度:★★☆☆☆
题目分析
输入输出
module top_module(
input clk,
input load,
input [1:0] ena, // 2位控制信号
input [99:0] data,
output reg [99:0] q
);功能需求
实现100位循环移位寄存器:
ena = 2'b01: 右循环移位ena = 2'b10: 左循环移位ena = 2'b00/2'b11: 不移位
关键区别:循环移位不丢失数据,移出的位补到另一端
核心知识点
知识点:循环移位 vs 普通移位
// 普通右移(高位补0)
q <= q >> 1; // [99:0] -> [0, 99:1]
// 循环右移(高位补最低位)
q <= {q[0], q[99:1]}; // [99:0] -> [0, 99:1]
// 循环左移(低位补最高位)
q <= {q[98:0], q[99]}; // [99:0] -> [98:0, 99]图解:
原始: [A][B][C][D]
右移: [0][A][B][C] D丢失
右循环: [D][A][B][C] D移到首位️ 解题思路
module top_module(
input clk,
input load,
input [1:0] ena,
input [99:0] data,
output reg [99:0] q
);
always @(posedge clk) begin
if (load)
q <= data;
else begin
case (ena)
2'b01: q <= {q[0], q[99:1]}; // 右循环
2'b10: q <= {q[98:0], q[99]}; // 左循环
default: q <= q; // 保持
endcase
end
end
/* ========== 代码逻辑深度解析 ==========
*
* 1. 为什么这是同步复位设计?
* 注意敏感列表只有"posedge clk",没有复位信号!这意味着:
* - load信号需要等待时钟上升沿才能生效
* - 这种设计更稳定,避免了异步信号的竞争问题
*
* 2. 循环移位的位拼接原理:
* 右循环:{q[0], q[99:1]}
* - q[0]:最低位移到最高位
* - q[99:1]:原数组整体右移,空出最高位位置
* - 结果:[原q0, 原q99, 原q98, ..., 原q1]
*
* 左循环:{q[98:0], q[99]}
* - q[98:0]:原数组整体左移,空出最低位位置
* - q[99]:最高位移到最低位
* - 结果:[原q98, ..., 原q0, 原q99]
*
* 3. 为什么不用移位操作符?
* 移位操作符"<<"和">>"会丢弃移出的位:
* q >> 1 会得到 [0, q99, q98, ..., q1],q[0]永远丢失!
* 循环移位需要保留所有数据,所以必须用位拼接。
*
* 4. case语句的default为什么重要?
* 防止生成锁存器(latch)!如果case不完整,综合器会生成锁存器来保持值,
* 这会带来功耗增加、时序问题等风险。default确保所有情况都被覆盖。
*
* 5. 为什么用{}而不是其他方法?
* {}是Verilog的位拼接操作符,硬件效率最高:
* - 直接连线,没有组合逻辑
* - 延迟最小,适合高速设计
* - 综合器能很好地优化
*/
endmoduleSubmit状态:
⚠️ 易错点总结
位拼接顺序错误
// ❌ 错误 q <= {q[99:1], q[0]}; // 这是左循环,不是右循环 // ✅ 正确 q <= {q[0], q[99:1]}; // 右循环使用移位操作符
// ⚠️ 不推荐:移位会导致位宽变化 q <= (q << 1) | (q[99]); // 复杂且易错 // ✅ 推荐:直接位拼接 q <= {q[98:0], q[99]};
题目3:Left/right arithmetic shift by 1 or 8
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Shift18
- 标签:
#算术移位#符号扩展 - 难度:★★★☆☆
题目分析
输入输出
module top_module(
input clk,
input load,
input ena,
input [1:0] amount, // 控制移位方向和位数
input [63:0] data,
output reg [63:0] q
);功能需求
实现64位算术移位寄存器:
amount = 2'b00: 左移1位amount = 2'b01: 左移8位amount = 2'b10: 算术右移1位(符号扩展)amount = 2'b11: 算术右移8位(符号扩展)
核心知识点
知识点:算术移位
定义:保留符号位的移位操作
// 逻辑右移:高位补0
q <= q >> 1; // [63:0] -> [0, 63:1]
// 算术右移:高位补符号位
q <= {q[63], q[63:1]}; // 保留符号
// 算术右移8位:高位补8个符号位
q <= {{8{q[63]}}, q[63:8]};示例:
数值: 11000 (-8 in signed)
逻辑>>1: 01100 (12) ❌ 错误
算术>>1: 11100 (-4) ✅ 正确,相当于÷2️ 解题思路
module top_module(
input clk,
input load,
input ena,
input [1:0] amount,
input [63:0] data,
output reg [63:0] q
);
always @(posedge clk) begin
if (load)
q <= data;
else if (ena) begin
case (amount)
2'b00: q <= q << 1; // 左移1位
2'b01: q <= q << 8; // 左移8位
2'b10: q <= {q[63], q[63:1]}; // 算术右移1位
2'b11: q <= {{8{q[63]}}, q[63:8]}; // 算术右移8位
endcase
end
end
/* ========== 代码逻辑深度解析 ==========
*
* 1. 为什么左移用"<<",右移用位拼接?
* 左移:"q << 1"和"q << 8"会自动在低位补0,这符合算术左移的要求。
* 右移:必须用位拼接实现符号扩展,因为">>>"操作符在某些综合器中支持不好。
*
* 2. 算术右移的符号扩展原理:
* 右移1位:{q[63], q[63:1]}
* - q[63]:符号位(最高位)
* - q[63:1]:原数据右移,空出最低位
* - 结果:最高位填符号位,其他位右移
*
* 右移8位:{{8{q[63]}}, q[63:8]}
* - {8{q[63]}}:复制符号位8次!这是关键技巧
* - q[63:8]:原数据右移8位
* - 结果:高位填8个符号位,低位右移8位
*
* 3. 符号扩展为什么重要?
* 算术移位用于有符号数运算,必须保持数值的数学意义:
* 例:11000(-8) >> 1 = 11100(-4),相当于除以2
* 如果用逻辑移位:01100(12),数值完全错误!
*
* 4. 重复操作符{}的妙用:
* "{8{q[63]}}"表示"将q[63]重复8次":
* 如果q[63]=0:{8{1'b0}} = 8'b00000000
* 如果q[63]=1:{8{1'b1}} = 8'b11111111
* 这正是符号扩展需要的!
*
* 5. 为什么amount的编码是这样的?
* 2'b00: 左移1位(最小操作)
* 2'b01: 左移8位(较大操作)
* 2'b10: 右移1位(最高位为1表示右移)
* 2'b11: 右移8位(最大操作)
* 这是HDLBits题目的特定编码,理解即可。
*/
endmoduleSubmit状态: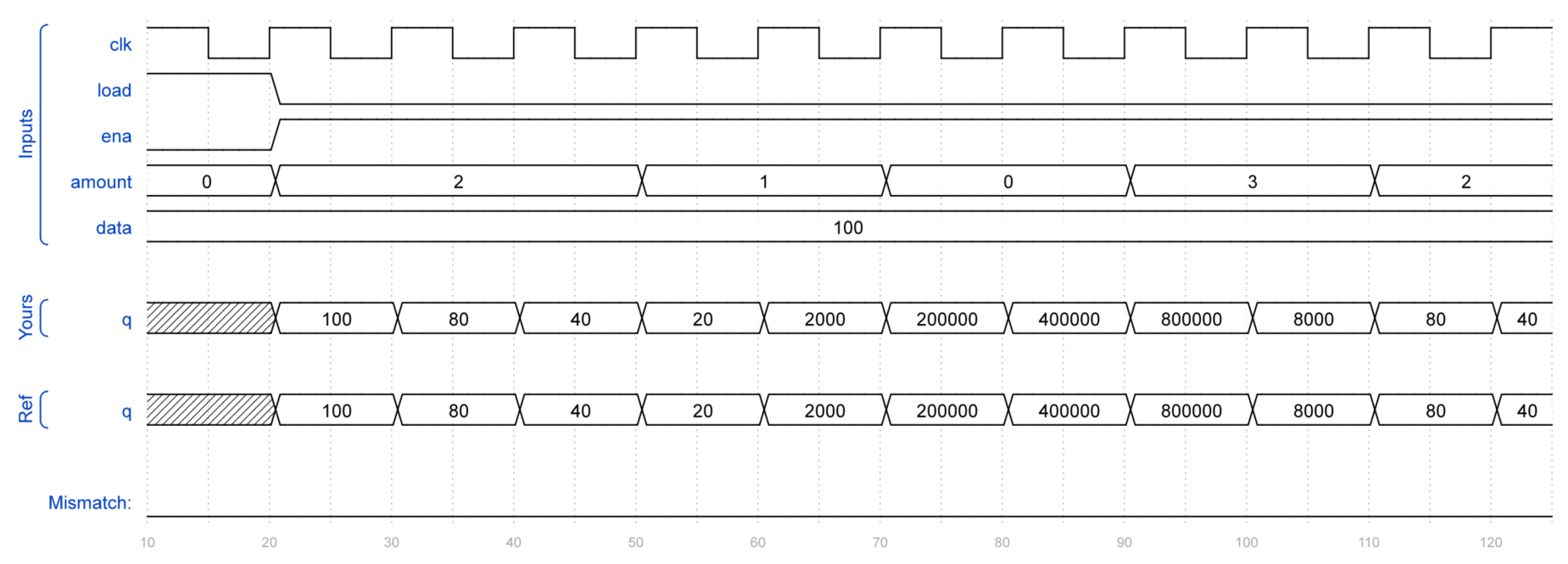
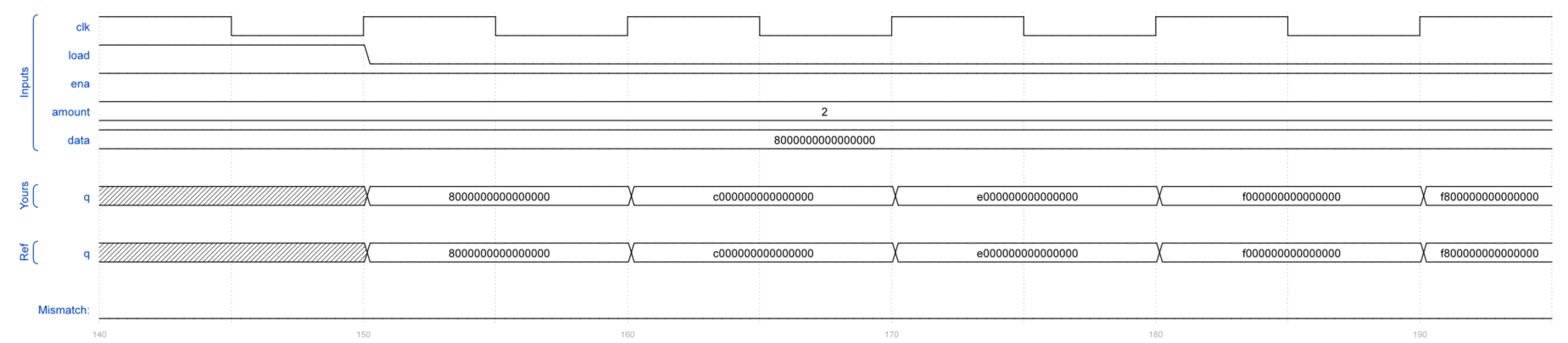
方法对比
| 操作 | 实现方式 | 说明 |
|---|---|---|
| 左移1位 | q << 1 | 低位补0 |
| 算术右移1位 | {q[63], q[63:1]} | 高位补符号位 |
| 算术右移8位 | {{8{q[63]}}, q[63:8]} | 复制符号位8次 |
题目4:5-bit LFSR
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Lfsr5
- 标签:
#LFSR#伪随机数#Galois结构 - 难度:★★★☆☆
题目分析
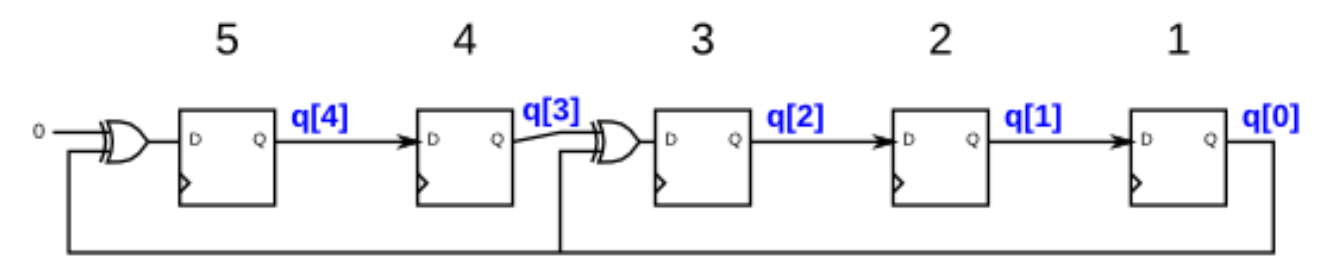
输入输出
module top_module(
input clk,
input reset, // 同步复位到5'h1
output [4:0] q
);功能需求
实现5位最大长度Galois LFSR,tap位置在第5位和第3位
LFSR原理:
- 通过XOR反馈生成伪随机序列
- 周期:2^5-1 = 31个状态
- 起始状态:5’h1 (00001)
电路图解
[q4] --XOR(0)-- [q3] --XOR(q0)-- [q2] -- [q1] -- [q0]
^ |
|_______________________________________________|核心知识点
知识点:LFSR结构
Galois LFSR特点:
- 有"tap"位置与输出位XOR
- 无"tap"位置直接移位
- 所有反馈同时进行
状态转移:
初始: 00001
步骤1: 10100 (q0=1触发tap3和tap5的XOR)
步骤2: 01010
步骤3: 00101
...
31步后回到: 00001️ 解题思路
module top_module(
input clk,
input reset,
output reg [4:0] q
);
always @(posedge clk) begin
if (reset)
q <= 5'h1;
else begin
// Galois LFSR结构
q[4] <= 1'b0 ^ q[0]; // tap5: XOR with q0
q[3] <= q[4]; // 直接移位
q[2] <= q[3] ^ q[0]; // tap3: XOR with q0
q[1] <= q[2]; // 直接移位
q[0] <= q[1]; // 直接移位
end
end
/* ========== 代码逻辑深度解析 ==========
*
* 1. Galois LFSR的工作原理:
* Galois结构的特点是"tap位置进行XOR,其他位置直接移位":
* - 反馈信号:q[0](最低位)
* - tap位置:第5位(q[4])和第3位(q[2])
* - 非tap位置:直接从左边移位过来
*
* 2. 为什么用"q[4] <= 1'b0 ^ q[0]"?
* 题目图中第5位的tap连接到0(地),所以:
* q[4]的新值 = q[0] XOR 0 = q[0]
* 这相当于把q[0]直接反馈到最高位!
*
* 3. 为什么用"q[2] <= q[3] ^ q[0]"?
* 第3位是真正的tap位置,需要与反馈信号XOR:
* q[2]的新值 = q[3](从左边移位过来) XOR q[0](反馈)
* 这正是LFSR的核心:线性反馈!
*
* 4. 为什么其他位是直接移位?
* q[3] <= q[4]:从q[4]移位过来
* q[1] <= q[2]:从q[2]移位过来
* q[0] <= q[1]:从q[1]移位过来
* 这些位置没有tap,所以直接传递。
*
* 5. 为什么复位到5'h1?
* LFSR绝对不能复位到全0!原因:
* - 全0状态下,q[0]=0
* - 所有XOR操作:0 XOR 0 = 0
* - 结果永远保持全0,陷入死锁状态
* - 必须复位到非零值才能生成伪随机序列
*
* 6. 这个LFSR的周期是多少?
* 5位最大长度LFSR的周期是2^5-1=31,也就是说会生成31个不同的
* 状态然后回到初始状态,这就是"伪随机"序列。
*
* 7. 为什么这种写法比位拼接好?
* 虽然位拼接更简洁,但这种逐位赋值更清晰:
* - 明确显示每个位的操作
* - 便于调试和理解
* - 硬件综合结果相同
*/
// 方案2:使用位拼接(更简洁)
// always @(posedge clk) begin
// if (reset)
// q <= 5'h1;
// else
// q <= {q[0]^1'b0, q[4], q[3]^q[0], q[2], q[1]};
// end
endmoduleSubmit状态: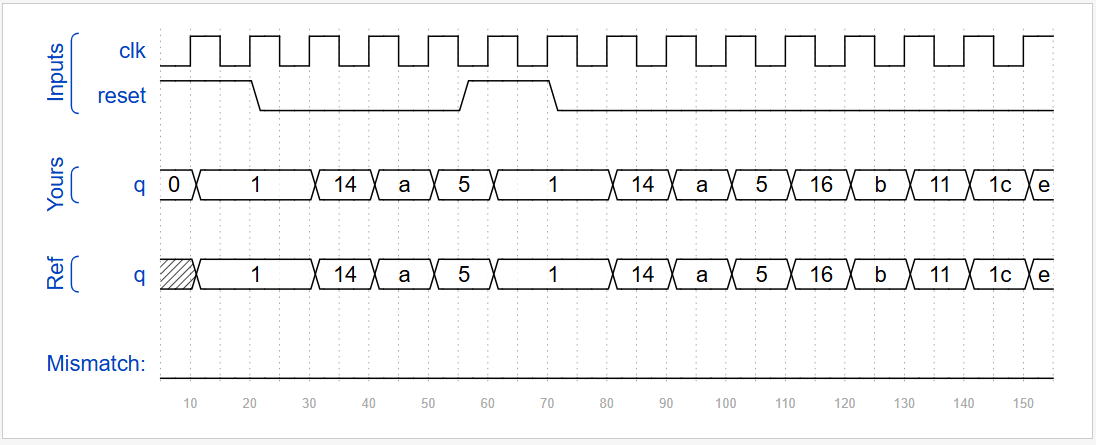
⚠️ 易错点总结
- XOR顺序混淆
- tap5的XOR输入是0,所以
q[4] <= q[0] - tap3需要XOR,所以
q[2] <= q[3] ^ q[0]
- tap5的XOR输入是0,所以
- 复位值错误
- 不能复位到全0(会卡死)
- 必须复位到非零值,如
5'h1
题目5:3-bit LFSR
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Mt2015_lfsr
- 标签:
#LFSR#模块设计 - 难度:★★☆☆☆
题目分析
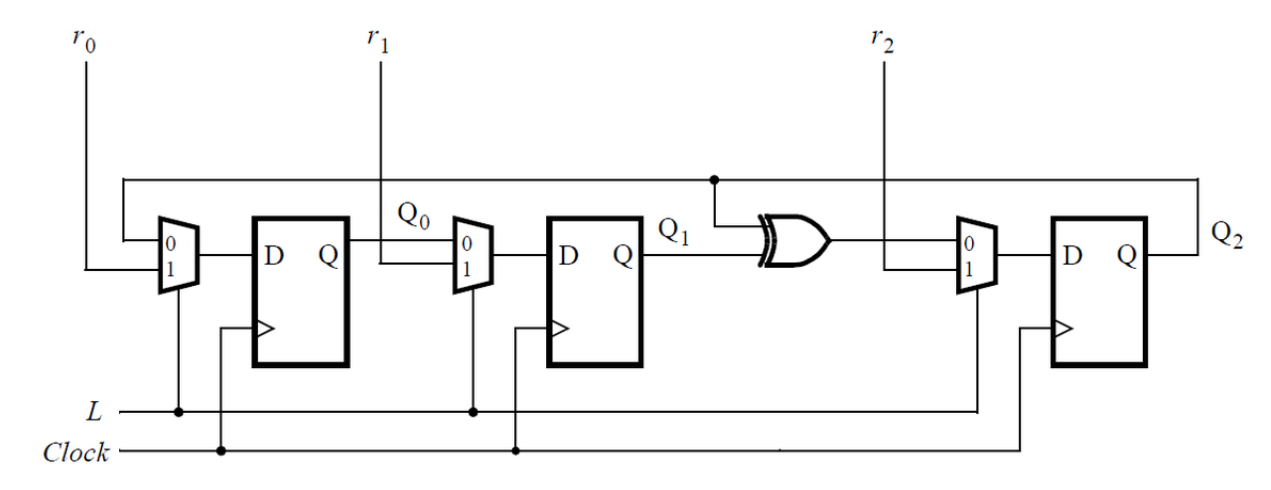
输入输出
module top_module(
input [2:0] SW, // R输入(连接开关)
input [1:0] KEY, // KEY[0]=clk, KEY[1]=L
output reg [2:0] LEDR // Q输出(连接LED)
);功能需求
实现3位LFSR,DE1-SoC板接口:
KEY[1](L=1): 加载SW到寄存器KEY[1](L=0): LFSR反馈模式- 反馈:
LEDR[2] <= LEDR[2] ^ LEDR[1]
️ 解题思路
module top_module(
input [2:0] SW,
input [1:0] KEY,
output reg [2:0] LEDR
);
always @(posedge KEY[0]) begin
if (KEY[1]) begin
// 加载模式
LEDR <= SW;
end else begin
// LFSR模式
LEDR[2] <= LEDR[2] ^ LEDR[1];
LEDR[1] <= LEDR[0];
LEDR[0] <= LEDR[2];
end
end
endmodule/* ========== 代码逻辑深度解析 ==========
*
* 1. 这是3位LFSR的Fibonacci结构实现:
* 反馈多项式:x³ + x² + 1(tap位置3和2)
* 反馈位置:最高位LEDR[2]
*
* 2. LFSR模式下的数据流分析:
* LEDR[2] <= LEDR[2] ^ LEDR[1](反馈:tap2 XOR tap1)
* LEDR[1] <= LEDR[0] (移位:从最低位移过来)
* LEDR[0] <= LEDR[2] (移位:原最高位移到最低位)
*
* 3. 注意这里的特殊之处:
* LEDR[0] <= LEDR[2] 使用的是旧值!
* 这是正确的,因为所有赋值都是同时发生的:
* 新LED[2] = 旧LED[2] XOR 旧LED[1]
* 新LED[1] = 旧LED[0]
* 新LED[0] = 旧LED[2]
*
* 4. 为什么这种结构有效?
* 这实际上是一个循环反馈:
* LEDR[2]被用作反馈,同时又被移位到LEDR[0]
* 这样保证了反馈信号能够持续传播
*
* 5. 状态序列示例(假设从001开始):
* 001 → 101 → 111 → 011 → 110 → 011 → 101 → 001
* 周期为7(2³-1),这是最大长度LFSR
*
* 6. DE1-SoC板接口的理解:
* KEY[0]: 时钟信号(手动按键)
* KEY[1]: 模式选择(1=加载,0=LFSR)
* SW: 并行数据输入(用于初始化)
* LEDR: 输出显示(显示当前LFSR状态)
*/Submit状态:
题目6:32-bit LFSR
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Lfsr32
- 标签:
#LFSR#大规模设计 - 难度:★★★☆☆
题目分析
输入输出
module top_module(
input clk,
input reset,
output reg [31:0] q
);功能需求
实现32位Galois LFSR,tap位置:32, 22, 2, 1
️ 解题思路
module top_module(
input clk,
input reset,
output reg [31:0] q
);
reg [31:0] q_next;
// 组合逻辑:计算下一状态
always @(*) begin
q_next = q[31:1]; // 默认右移
q_next[31] = q[0] ^ 1'b0; // tap32
q_next[21] = q[0] ^ q[22]; // tap22
q_next[1] = q[0] ^ q[2]; // tap2
q_next[0] = q[0] ^ q[1]; // tap1
end
// 时序逻辑:更新寄存器
always @(posedge clk) begin
if (reset)
q <= 32'h1;
else
q <= q_next;
end
endmodule/* ========== 代码逻辑深度解析 ==========
*
* 1. 这种实现方式的优点(分离组合和时序逻辑):
* - 清晰性:组合逻辑和时序逻辑分离,代码更易读
* - 调试性:可以在仿真中观察q_next的值
* - 优化性:综合器能更好地优化组合逻辑部分
*
* 2. 32位Galois LFSR的反馈多项式:
* x³² + x²² + x² + x + 1
* tap位置:32, 22, 2, 1(对应q[31], q[21], q[1], q[0])
*
* 3. 代码逻辑分析:
* q_next = q[31:1]; // 默认右移1位,q[0]被丢弃
* q_next[31] = q[0] ^ 1'b0; // tap32: q[0] XOR 0 = q[0]
* q_next[21] = q[0] ^ q[22]; // tap22: q[0] XOR q[22]
* q_next[1] = q[0] ^ q[2]; // tap2: q[0] XOR q[2]
* q_next[0] = q[0] ^ q[1]; // tap1: q[0] XOR q[1]
*
* 4. 为什么tap32是q[0] ^ 1'b0?
* 与5位LFSR类似,第32位的tap连接到地(0)
* 所以反馈就是q[0]本身
*
* 5. 为什么周期是2³²-1?
* 这是最大长度LFSR的特征:
* - 使用本原多项式
* - 除了全0状态,所有2³²-1个状态都会出现
* - 周期长达42亿,适合伪随机数生成
*
* 6. 实际应用场景:
* - 通信系统:扩频序列生成
* - 加密系统:流密码密钥生成
* - 测试系统:伪随机测试向量
* - CRC计算:循环冗余校验
*/Submit状态:
题目7:Shift register(m2014_q4k)
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Exams/m2014_q4k
- 难度:★★☆☆☆
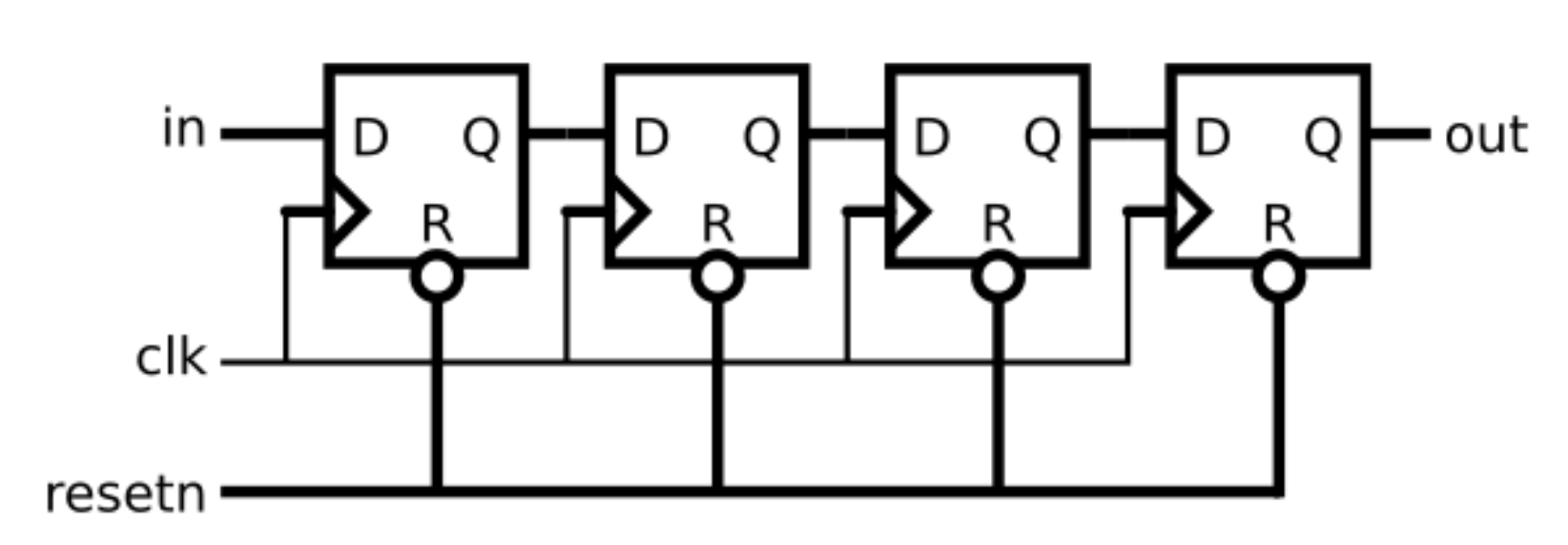
️ 解题思路
module top_module(
input clk,
input resetn, // 同步低电平复位
input in,
output reg out
);
reg [2:0] shift_reg;
always @(posedge clk) begin
if (!resetn) begin
shift_reg <= 3'b0;
out <= 0;
end else begin
shift_reg <= {in, shift_reg[2:1]};
out <= shift_reg[0];
end
end
endmodule/* ========== 代码逻辑深度解析 ==========
*
* 1. 这是一个3级移位寄存器,结构分析:
* in → [FF2] → [FF1] → [FF0] → out
* shift_reg[2] shift_reg[1] shift_reg[0]
*
* 2. 为什么用{in, shift_reg[2:1]}?
* 这个位拼接实现了右移操作:
* - shift_reg[2] ← in(新的输入)
* - shift_reg[1] ← shift_reg[2](原最高位)
* - shift_reg[0] ← shift_reg[1](原中间位)
* 结果:整体右移,原最低位被丢弃
*
* 3. 为什么输出是shift_reg[0]?
* out <= shift_reg[0]表示:
* - 输出的是移位前的最低位
* - 这正好是3级延迟后的输入信号
* - out信号比in信号晚3个时钟周期
*
* 4. 同步低电平复位的特点:
* if (!resetn) 表示低电平有效
* 敏感列表只有posedge clk,所以是同步复位
* 必须等待时钟上升沿才能复位
*
* 5. 时序关系图:
* 周期1: in=1 → shift_reg=100 → out=0
* 周期2: in=0 → shift_reg=010 → out=0
* 周期3: in=1 → shift_reg=101 → out=0
* 周期4: in=0 → shift_reg=010 → out=1 (延迟3个周期的in)
*/Submit状态:
题目8:Shift register(2014_q4b)
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Exams/2014_q4b
- 难度:★★★☆☆
题目分析
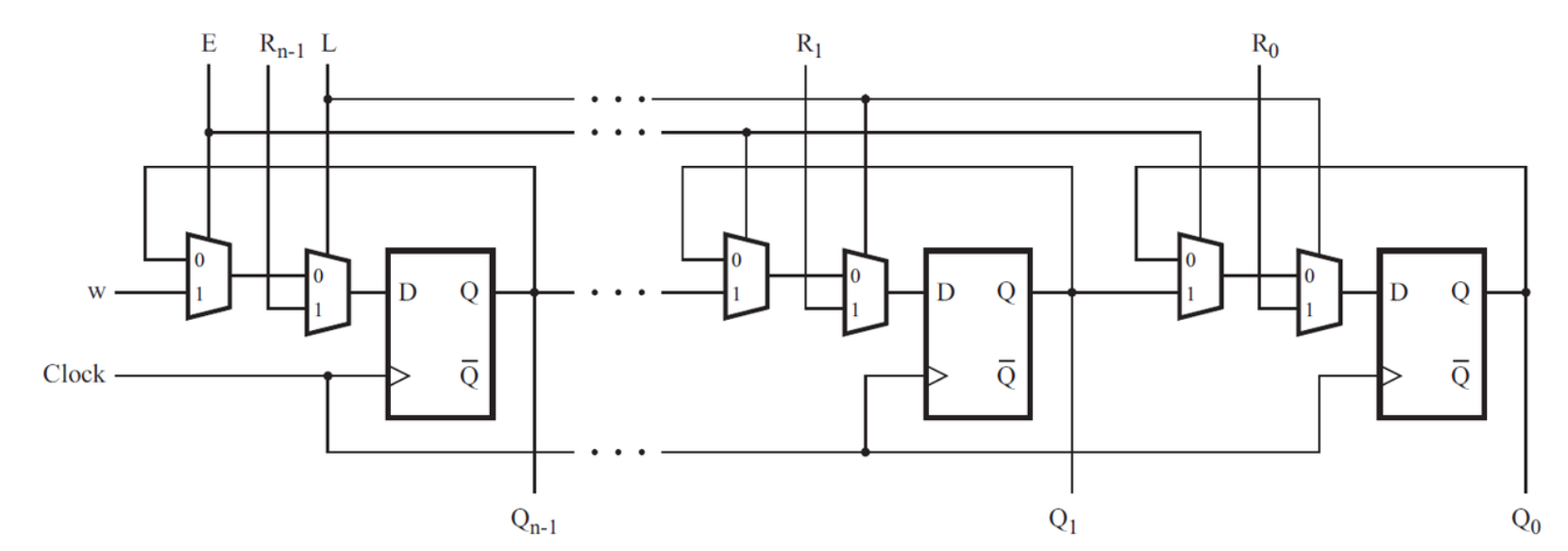
电路结构图
KEY[3] (w输入)
│
↓
┌────────┐ ┌────────┐ ┌────────┐ ┌────────┐
SW[3]→│MUXDFF3│→Q3→│MUXDFF2│→Q2→│MUXDFF1│→Q1→│MUXDFF0│→Q0
└────────┘ └────────┘ └────────┘ └────────┘
↓ ↓ ↓ ↓
LEDR[3] LEDR[2] LEDR[1] LEDR[0]
所有MUXDFF共享: clk=KEY[0], E=KEY[1], L=KEY[2]
注意:这是右移移位寄存器,数据从高位流向低位输入输出
verilog
module top_module(
input [3:0] SW, // SW连接到R输入(注意顺序)
input [3:0] KEY, // KEY[0]=clk, KEY[1]=E, KEY[2]=L, KEY[3]=w
output [3:0] LEDR // LED输出
);功能需求
实现4级右移移位寄存器:
- L=1:并行加载,
LEDR[i] <= SW[i] - L=0, E=1:串行右移,数据从KEY[3]进入LEDR[3],依次向右传递
- L=0, E=0:保持当前值
MUXDFF内部结构
E控制 L控制 时钟触发
w ──┐ ┌──┐ ┌──┐
├─MUX1──out1─┤ ├─MUX2──out2─┤ ├──→ Q
Q ──┘ │ │ │DFF│
R ─┘ └─out1 └──┘核心知识点
知识点1:MUXDFF的正确实现
错误实现(会导致组合环路):
verilog
// ❌ 错误:Q不能同时作为输入和输出
output reg Q;
always @(*) begin
mux1 = E ? w : Q; // Q在右边(读),左边也是Q(写)→组合环路!
end正确实现(分离组合逻辑和时序逻辑):
verilog
module MUXDFF(
input clk,
input w, R, E, L,
output reg Q
);
// 组合逻辑1:E控制的MUX
reg mux1;
always @(*) begin
if (E)
mux1 = w;
else
mux1 = Q; // 这里Q是读取当前状态
end
// 组合逻辑2:L控制的MUX
reg mux2;
always @(*) begin
if (L)
mux2 = R;
else
mux2 = mux1;
end
// 时序逻辑:DFF
always @(posedge clk) begin
Q <= mux2; // 这里Q是更新状态
end
endmodule关键点:
- 用中间变量
mux1和mux2打断组合环路 always @(*)用于组合逻辑always @(posedge clk)用于时序逻辑
知识点2:R输入的连接顺序
重要:R的连接不是简单的SW[i]→LEDR[i]!
观察电路图,右移移位寄存器的特点:
- 数据从高位流向低位
- 但每个触发器的加载值(R)应该对应其位置
正确连接:
verilog
LEDR[3] 的 R ← SW[3] // 高位对应高位
LEDR[2] 的 R ← SW[2]
LEDR[1] 的 R ← SW[1]
LEDR[0] 的 R ← SW[0] // 低位对应低位️ 解题思路
第一步:理解MUXDFF的两级MUX结构
输入w, Q, R, E, L → 输出Q
步骤1: E控制第一级MUX
if E=1: mux1 = w
if E=0: mux1 = Q (保持)
步骤2: L控制第二级MUX
if L=1: mux2 = R (加载)
if L=0: mux2 = mux1
步骤3: 时钟上升沿更新Q
Q <= mux2第二步:确定链式连接
右移移位寄存器:
KEY[3] → LEDR[3] → LEDR[2] → LEDR[1] → LEDR[0] → (丢弃)第三步:完整代码实现
module MUXDFF(
input clk,
input w, R, E, L,
output reg Q
);
// 第一级MUX:E选择w或Q
reg mux1;
always @(*) begin
if (E)
mux1 = w;
else
mux1 = Q;
end
// 第二级MUX:L选择R或mux1
reg mux2;
always @(*) begin
if (L)
mux2 = R;
else
mux2 = mux1;
end
// DFF:时钟上升沿更新
always @(posedge clk) begin
Q <= mux2;
end
endmodule
/* ========== 代码逻辑深度解析 ==========
*
* 1. 为什么要用两级MUX结构?
* 这是硬件设计的"功能分层"思想:
* - 第一级(E控制):选择"外部输入"或"自身保持"
* - 第二级(L控制):选择"并行加载"或"第一级输出"
* 优点:逻辑清晰,功能独立,便于测试和调试
*
* 2. 为什么用中间变量mux1和mux2?
* 关键原因:避免组合环路!
* 如果写成:always @(*) Q = E ? w : Q; // Q同时出现在左右边
* 会形成:Q → MUX → Q 的无限循环,综合器会报错或生成锁存器。
* 用中间变量打破了环路:Q → mux1 → mux2 → Q(时钟触发)
*
* 3. 为什么组合逻辑用always @(*)?
* always @(*)表示"组合逻辑",特点:
* - 任何输入变化都会立即重新计算
* - 综合为纯组合逻辑电路(门电路)
* - 没有"<<"阻塞赋值,避免时序问题
*
* 4. 为什么时序逻辑用always @(posedge clk)?
* always @(posedge clk)表示"时序逻辑",特点:
* - 只在时钟上升沿触发
* - 使用非阻塞赋值"<="
* - 综合为触发器(Flip-Flop)
*
* 5. 两级MUX的真值表分析:
* E | L | 最终输出Q
* 0 | 0 | Q(保持:保持→保持)
* 0 | 1 | R(加载:保持→并行数据)
* 1 | 0 | w(移位:外部输入→保持)
* 1 | 1 | R(加载:外部输入→并行数据,L优先级更高)
*
* 6. 为什么L优先级高于E?
* 从代码可以看出:mux2 = L ? R : mux1;
* 当L=1时,无论E是什么,都选择R(并行加��)。
* 这是合理的设计:加载操作通常比移位操作更重要。
*/
module MUXDFF(
input clk,
input w, R, E, L,
output reg Q
);
// 第一级MUX:E选择w或Q
reg mux1;
always @(*) begin
if (E)
mux1 = w;
else
mux1 = Q;
end
// 第二级MUX:L选择R或mux1
reg mux2;
always @(*) begin
if (L)
mux2 = R;
else
mux2 = mux1;
end
// DFF:时钟上升沿更新
always @(posedge clk) begin
Q <= mux2;
end
endmodule
module top_module(
input [3:0] SW,
input [3:0] KEY,
output [3:0] LEDR
);
// 实例化4个MUXDFF,形成右移移位寄存器
// 注意:R的连接是SW[3]→LEDR[3], SW[2]→LEDR[2]...
MUXDFF MUXDFF_0(
.clk(KEY[0]),
.w(KEY[3]), // 最高位接收外部输入
.R(SW[3]), // 加载SW[3]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[3])
);
MUXDFF MUXDFF_1(
.clk(KEY[0]),
.w(LEDR[3]), // 从LEDR[3]接收
.R(SW[2]), // 加载SW[2]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[2])
);
MUXDFF MUXDFF_2(
.clk(KEY[0]),
.w(LEDR[2]), // 从LEDR[2]接收
.R(SW[1]), // 加载SW[1]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[1])
);
MUXDFF MUXDFF_3(
.clk(KEY[0]),
.w(LEDR[1]), // 从LEDR[1]接收
.R(SW[0]), // 加载SW[0]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[0])
);
endmoduleSubmit状态:
第四步:验证逻辑
测试用例1:加载操作
L=1, SW=4'b1010
→ LEDR[3]=1, LEDR[2]=0, LEDR[1]=1, LEDR[0]=0
→ LEDR = 4'b1010 ✓测试用例2:右移操作
初始: LEDR=4'b1010
L=0, E=1, KEY[3]=1
→ LEDR[3]=1 (从KEY[3])
→ LEDR[2]=1 (从LEDR[3])
→ LEDR[1]=0 (从LEDR[2])
→ LEDR[0]=1 (从LEDR[1])
→ LEDR = 4'b1101 ✓⚠️ 易错点总结
- 组合环路问题
verilog
// ❌ 错误:Q同时读写导致环路
output reg Q;
always @(*) begin
Q = E ? w : Q; // 组合环路!
end
// ✅ 正确:使用中间变量
reg mux_out;
always @(*) begin
mux_out = E ? w : Q;
end
always @(posedge clk) begin
Q <= mux_out;
end- R连接顺序错误
verilog
// ❌ 错误思维:按照w的流向连接R
// LEDR[3]的R连接SW[0] ? 错!
// ✅ 正确:R是并行加载,对应位置连接
// LEDR[3]的R连接SW[3]
// LEDR[2]的R连接SW[2]
// ...- 移位方向混淆
verilog
// ⚠️ 这是右移!数据从高位→低位
// w → LEDR[3] → LEDR[2] → LEDR[1] → LEDR[0]
// 不是左移:
// w → LEDR[0] → LEDR[1] → LEDR[2] → LEDR[3]- always块类型错误
verilog
// ❌ 组合逻辑用时序always
always @(posedge clk) begin
mux1 = E ? w : Q; // 应该用always @(*)
end
// ✅ 正确
always @(*) begin // 组合逻辑
mux1 = E ? w : Q;
end
always @(posedge clk) begin // 时序逻辑
Q <= mux1;
end进阶思考
思考题1:为什么要分两级MUX?
点击查看答案原因:控制优先级和功能独立性
- 第一级MUX(E控制):选择"移位"或"保持"
- 第二级MUX(L控制):选择"加载"或"前级输出"
如果合并成一级:
verilog
// 合并后需要复杂的条件判断
if (L) Q <= R;
else if (E) Q <= w;
else Q <= Q;分离后更清晰:
verilog
mux1 = E ? w : Q; // 移位/保持
mux2 = L ? R : mux1; // 加载/使用mux1结果思考题2:如何改为双向移位寄存器?
点击查看提示增加方向控制信号DIR:
- DIR=0:右移(当前实现)
- DIR=1:左移
关键:每个MUXDFF的w输入需要根据DIR选择来自左邻居或右邻居
✅ 点击查看答案 ```verilog module top_module_bidirectional( input [3:0] SW, input [3:0] KEY, // 假设KEY[3]作为DIR input DIR, // 0=右移, 1=左移 output [3:0] LEDR ); wire [3:0] w_in;// 根据方向选择每级的w输入
assign w_in[3] = DIR ? 1'b0 : KEY[3]; // 右移时从KEY[3]输入
assign w_in[2] = DIR ? LEDR[1] : LEDR[3]; // 左移从LEDR[1],右移从LEDR[3]
assign w_in[1] = DIR ? LEDR[0] : LEDR[2];
assign w_in[0] = DIR ? 1'b0 : LEDR[1]; // 左移时从低位输入0
MUXDFF d3(.clk(KEY[0]), .w(w_in[3]), .R(SW[3]), .E(KEY[1]), .L(KEY[2]), .Q(LEDR[3]));
MUXDFF d2(.clk(KEY[0]), .w(w_in[2]), .R(SW[2]), .E(KEY[1]), .L(KEY[2]), .Q(LEDR[2]));
MUXDFF d1(.clk(KEY[0]), .w(w_in[1]), .R(SW[1]), .E(KEY[1]), .L(KEY[2]), .Q(LEDR[1]));
MUXDFF d0(.clk(KEY[0]), .w(w_in[0]), .R(SW[0]), .E(KEY[1]), .L(KEY[2]), .Q(LEDR[0]));
endmoduleenvar i;
generate
for (i = 0; i < N; i = i + 1) begin : shift_stage
MUXDFF dff(
.clk(KEY[0]),
.w(chain[i]),
.R(SW[i]),
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[i])
);
assign chain[i+1] = LEDR[i];
end
endgenerate
endmodule题目9:3-input LUT
题目信息
- 链接:https://hdlbits.01xz.net/wiki/Exams/ece241_2013_q12
- 难度:★★★☆☆
题目分析
LUT原理:查找表(Look-Up Table),用RAM实现任意逻辑
module top_module(
input clk,
input enable,
input S,
input A, B, C,
output reg Z
);
reg [7:0] q; // 8-bit shift register
always @(posedge clk) begin
if (enable)
q <= {q[6:0], S}; // 串行输入
end
// LUT输出
always @(*) begin
case ({A,B,C})
3'b000: Z = q[0];
3'b001: Z = q[1];
3'b010: Z = q[2];
3'b011: Z = q[3];
3'b100: Z = q[4];
3'b101: Z = q[5];
3'b110: Z = q[6];
3'b111: Z = q[7];
endcase
end
endmodule
/* ========== 代码逻辑深度解析 ==========
*
* 1. LUT的本质是什么?
* LUT(Look-Up Table)本质是一个可编程的8:1多路复用器:
* - 地址:{A,B,C}构成3位地址(2^3=8种组合)
* - 存储内容:q[7:0]的8个位
* - 输出:根据地址选择对应的数据位
*
* 2. 为什么用移位寄存器+LUT的组合?
* 这是一个巧妙的设计:
* - 移位寄存器:动态更新LUT的内容
* - LUT:实现任意3输入逻辑函数
* - 效果:可以动态重构的逻辑函数!
*
* 3. 移位寄存器的工作原理:
* q <= {q[6:0], S} 表示:
* - q[7:1] ← q[6:0](右移1位)
* - q[0] ← S(新的串行输入)
* - q[7]被丢弃
* 这样每个时钟周期都会更新LUT的一个"存储单元"
*
* 4. LUT地址映射的实现:
* {A,B,C}作为3位地址:
* 000 → q[0](最低位)
* 001 → q[1]
* ...
* 111 → q[7](最高位)
* 这就是标准的二进制地址映射!
*
* 5. 为什么LUT在FPGA中很重要?
* - 通用性:可以实现任意布尔函数
* - 高效:查找表速度比门级网络快
* - 可重构:通过改变存储内容改变功能
* 这是现代FPGA的基本构建单元!
*
* 6. 这个设计的实际应用场景:
* - 动态逻辑:可以根据需要改变逻辑功能
* - 序列检测:不同的输入序列触发不同输出
* - 自适应滤波:根据统计特性调整滤波器参数
*
* 7. 为什么要用always @(*)?
* 因为LUT是纯组���逻辑:
* - 输入({A,B,C}和q)变化应立即反映到输出Z
* - 没有时钟延迟,这是查找表的基本特性
* - 综合器会生成8:1 MUX电路
*/Submit状态: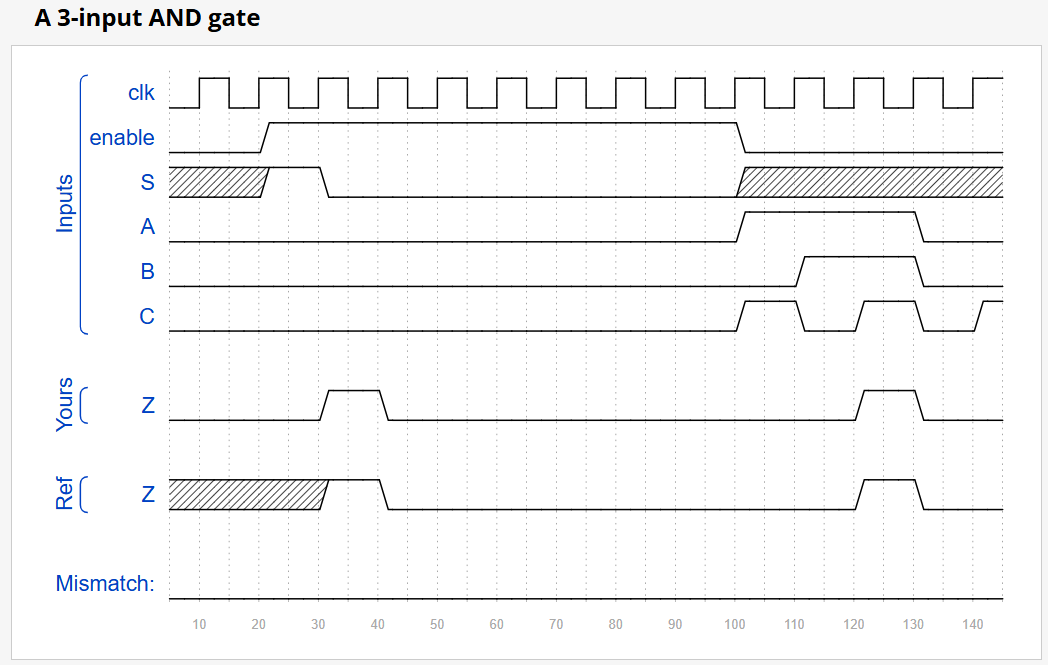
本章总结
核心要点速记
✅ 移位寄存器:使用 >> << 或位拼接实现
✅ 循环移位:{q[0], q[n:1]} 不丢失数据
✅ 算术移位:保留符号位 {q[n], q[n:1]}
✅ LFSR:通过XOR反馈生成伪随机序列,周期2^n-1易错点口诀
右移低位丢,循环两头接 算术要符号,逻辑全补零 LFSR看清tap,全零状态莫入坑
学习检查清单
- 理解普通移位、循环移位、算术移位的区别
- 掌握位拼接操作符
{}的用法 - 能独立实现LFSR并理解其工作原理
- 熟练使用case语句实现多路选择
下一步学习
推荐阅读:Counters章节 - 学习计数器设计
实战项目:LFSR随机数生成器应用
问题讨论:评论区/论坛
扩展资源
移位寄存器深入理解
1. 应用场景
- 串行通信:UART、SPI数据收发
- 流水线缓冲:数据延迟、时序对齐
- 伪随机数:LFSR用于测试向量生成
- CRC校验:循环冗余校验码计算
2. LFSR多项式对照表
| 位宽 | 多项式 | Tap位置 | 周期 |
|---|---|---|---|
| 3位 | x³+x²+1 | [3,2] | 7 |
| 5位 | x⁵+x³+1 | [5,3] | 31 |
| 8位 | x⁸+x⁶+x⁵+x⁴+1 | [8,6,5,4] | 255 |
| 16位 | x¹⁶+x¹⁵+x¹³+x⁴+1 | [16,15,13,4] | 65535 |
| 32位 | x³²+x²²+x²+x+1 | [32,22,2,1] | 4294967295 |
3. 性能优化技巧
技巧1:流水线优化
// 原始代码(关键路径长)
always @(posedge clk) begin
q <= {q[62:0], complex_function(q[63])};
end
// 优化:插入寄存器打断长路径
always @(posedge clk) begin
temp <= complex_function(q[63]);
end
always @(posedge clk) begin
q <= {q[62:0], temp};
end技巧2:参数化设计
module shift_register #(
parameter WIDTH = 8,
parameter DEPTH = 4
)(
input clk,
input [WIDTH-1:0] in,
output [WIDTH-1:0] out
);
reg [WIDTH-1:0] regs [0:DEPTH-1];
always @(posedge clk) begin
regs[0] <= in;
for (int i=1; i
进阶挑战题
挑战1:可配置方向移位寄存器
需求:设计8位移位寄存器,支持:
- 左移/右移可选
- 移位量可配置(1-8位)
- 逻辑/算术移位模式切换
点击查看提示
// 提示:使用case语句分情况处理
case ({direction, shift_amount})
{1'b0, 3'd1}: q <= q << 1;
{1'b0, 3'd4}: q <= q << 4;
{1'b1, 3'd1}: q <= q >>> 1; // 算术右移
// ...
endcase
✅ 点击查看答案
module configurable_shifter(
input clk,
input reset,
input direction, // 0=左移, 1=右移
input arithmetic, // 0=逻辑, 1=算术
input [2:0] amount, // 移位量
input signed [7:0] data_in,
output reg signed [7:0] q
);
always @(posedge clk) begin
if (reset)
q <= 8'b0;
else begin
if (direction == 0) begin
// 左移(逻辑/算术相同)
q <= q << amount;
end else begin
// 右移
if (arithmetic)
q <= q >>> amount; // 算术右移
else
q <= q >> amount; // 逻辑右移
end
end
end
endmodule
挑战2:双向LFSR
需求:实现可正向/反向运行的16位LFSR
点击查看提示
反向LFSR需要"逆向"XOR操作,相当于左移而不是右移
✅ 点击查看答案
module bidirectional_lfsr(
input clk,
input reset,
input direction, // 0=forward, 1=backward
output reg [15:0] q
);
always @(posedge clk) begin
if (reset)
q <= 16'h1;
else if (direction == 0) begin
// 正向:Galois LFSR
q <= {q[0], q[15:1]};
q[15] <= q[0] ^ q[15];
q[13] <= q[0] ^ q[14];
q[12] <= q[0] ^ q[13];
q[10] <= q[0] ^ q[11];
end else begin
// 反向:逆向Galois LFSR
q <= {q[14:0], q[15]};
q[14] <= q[15] ^ q[14];
q[13] <= q[15] ^ q[13];
q[12] <= q[15] ^ q[12];
q[10] <= q[15] ^ q[10];
end
end
endmodule
挑战3:Johnson计数器
需求:设计4位Johnson计数器(扭环计数器)
特点:
- 状态序列:0000→0001→0011→0111→1111→1110→1100→1000→0000
- 周期:2N(N=位宽)
✅ 点击查看答案
module johnson_counter(
input clk,
input reset,
output reg [3:0] q
);
always @(posedge clk) begin
if (reset)
q <= 4'b0000;
else
q <= {q[2:0], ~q[3]}; // 左移+反码反馈
end
endmodule
实用工具与仿真
在线仿真验证
EDA Playground测试代码:
module testbench;
reg clk = 0;
reg reset = 1;
wire [4:0] q;
// 实例化LFSR
top_module dut(clk, reset, q);
// 时钟生成
always #5 clk = ~clk;
// 测试激励
initial begin
$dumpfile("wave.vcd");
$dumpvars(0, testbench);
#10 reset = 0;
#320 $finish; // 运行32个周期
end
// 监控输出
always @(posedge clk) begin
$display("Time=%0t q=%b", $time, q);
end
endmodule
波形分析要点
检查项:
- ✅ 复位后状态是否正确
- ✅ LFSR是否在31个周期后循环
- ✅ 是否出现全0状态(错误)
- ✅ 移位方向是否正确
互动区
常见问题FAQ
Q1:为什么LFSR不能复位到全0?
A:全0是LFSR的"死状态"。因为0⊕0=0,一旦进入全0状态就会永远卡在0,无法生成伪随机序列。通常复位到0x1或0xFFFF等非零值。
Q2:Galois型和Fibonacci型LFSR有什么区别?
A:
- Galois型:反馈分布在各级之间,适合硬件实现,延迟小
- Fibonacci型:反馈集中在输入端,结构简单但延迟大
Q3:如何选择LFSR的tap位置?
A:使用本原多项式(primitive polynomial),保证最大周期2^n-1。常用多项式可查数学手册,或使用在线生成器。
Q4:移位寄存器能用于数据延迟吗?
A:可以!N级移位寄存器可产生N个时钟周期的延迟。常用于时序对齐、流水线同步等场景。
Q5:算术移位与逻辑移位在RTL综合时有区别吗?
A:有区别:
- 逻辑移位:综合为简单的布线+补0
- 算术移位:综合为MUX+符号扩展逻辑,资源稍多
学习打卡
完成日期:________
⏱️ 用时:____分钟
完成题数:__/9
心得:
- 最难的题目:________________
- 关键收获:__________________
- 需要复习:__________________
知识关联图
代码模板库
模板1:通用N位移位寄存器
module generic_shift_register #(
parameter WIDTH = 8
)(
input clk,
input reset,
input shift_en,
input serial_in,
output serial_out,
output [WIDTH-1:0] parallel_out
);
reg [WIDTH-1:0] shift_reg;
always @(posedge clk or posedge reset) begin
if (reset)
shift_reg <= {WIDTH{1'b0}};
else if (shift_en)
shift_reg <= {serial_in, shift_reg[WIDTH-1:1]};
end
assign serial_out = shift_reg[0];
assign parallel_out = shift_reg;
endmodule
模板2:可配置LFSR生成器
module lfsr_generator #(
parameter WIDTH = 8,
parameter [WIDTH-1:0] POLYNOMIAL = 8'b10111000 // x^8+x^6+x^5+x^4+1
)(
input clk,
input reset,
input enable,
output reg [WIDTH-1:0] lfsr_out
);
wire feedback;
assign feedback = lfsr_out[0];
always @(posedge clk or posedge reset) begin
if (reset)
lfsr_out <= {{(WIDTH-1){1'b0}}, 1'b1}; // 初始化为1
else if (enable) begin
for (int i = 0; i < WIDTH-1; i++) begin
if (POLYNOMIAL[i+1])
lfsr_out[i+1] <= lfsr_out[i+2] ^ feedback;
else
lfsr_out[i+1] <= lfsr_out[i+2];
end
lfsr_out[0] <= feedback;
end
end
endmodule
模板3:桶形移位器(Barrel Shifter)
module barrel_shifter #(
parameter WIDTH = 8
)(
input [WIDTH-1:0] data_in,
input [$clog2(WIDTH)-1:0] shift_amount,
input direction, // 0=left, 1=right
input arithmetic, // 0=logical, 1=arithmetic
output reg [WIDTH-1:0] data_out
);
always @(*) begin
if (direction == 0)
data_out = data_in << shift_amount;
else begin
if (arithmetic && data_in[WIDTH-1])
data_out = (data_in >> shift_amount) |
({WIDTH{1'b1}} << (WIDTH - shift_amount));
else
data_out = data_in >> shift_amount;
end
end
endmodule
性能对比与选择
移位实现方式对比
实现方式 资源消耗 速度 灵活性 适用场景 移位操作符<< 低 快 低 固定移位量 位拼接{} 低 快 中 简单循环移位 桶形移位器 高 快 高 可变移位量 for循环 中 中 高 参数化设计
选择建议:
- 小规模固定移位:直接用
<<或>> - 循环移位:用位拼接
{}最清晰 - 可变移位量:用桶形移位器
- 参数化设计:用for循环生成
本章完成!
你已经掌握:
✅ 4种移位寄存器类型(基础/循环/算术/LFSR)
✅ 3种实现方式(操作符/拼接/模块化)
✅ 9道HDLBits经典题目
✅ 伪随机数生成器原理
进阶方向:
Level 1:学习Counters章节,理解计数器与移位器的结合
Level 2:深入FSM,设计复杂序列检测器
Level 3:实战项目 - CRC校验码生成器
相关文章推荐
进阶阅读:
- LFSR在FPGA中的高级应用 - CRC、加密、测试向量
- 数字电路时序分析- 关键路径优化
- SystemVerilog参数化设计- 可重用代码库
恭喜完成Shift Registers章节!
掌握移位寄存器是数字设计的重要里程碑!
觉得有帮助请点赞⭐ 收藏 评论
标签:#HDLBits#Verilog#移位寄存器#LFSR#FPGA#数字电路#零基础教程
附录:完整代码合集
A1. 所有题目完整代码
// ========== 题目1: 4-bit shift register ==========
module shift4(
input clk,
input areset,
input load,
input ena,
input [3:0] data,
output reg [3:0] q
);
always @(posedge clk or posedge areset) begin
if (areset)
q <= 4'b0;
else if (load)
q <= data;
else if (ena)
q <= q >> 1;
end
endmodule
// ========== 题目2: Left/right rotator ==========
module rotate100(
input clk,
input load,
input [1:0] ena,
input [99:0] data,
output reg [99:0] q
);
always @(posedge clk) begin
if (load)
q <= data;
else case (ena)
2'b01: q <= {q[0], q[99:1]}; // 右循环
2'b10: q <= {q[98:0], q[99]}; // 左循环
default: q <= q;
endcase
end
endmodule
// ========== 题目3: Arithmetic shift ==========
module shift18(
input clk,
input load,
input ena,
input [1:0] amount,
input [63:0] data,
output reg [63:0] q
);
always @(posedge clk) begin
if (load)
q <= data;
else if (ena) case (amount)
2'b00: q <= q << 1;
2'b01: q <= q << 8;
2'b10: q <= {q[63], q[63:1]};
2'b11: q <= {{8{q[63]}}, q[63:8]};
endcase
end
endmodule
// ========== 题目4: 5-bit LFSR ==========
module lfsr5(
input clk,
input reset,
output reg [4:0] q
);
always @(posedge clk) begin
if (reset)
q <= 5'h1;
else
q <= {1'b0^q[0], q[4], q[3]^q[0], q[2:1]};
end
endmodule
// ========== 题目5: 3-bit LFSR ==========
module mt2015_lfsr(
input [2:0] SW,
input [1:0] KEY,
output reg [2:0] LEDR
);
always @(posedge KEY[0]) begin
if (KEY[1])
LEDR <= SW;
else
LEDR <= {LEDR[1]^LEDR[2], LEDR[0], LEDR[2]};
end
endmodule
// ========== 题目6: 32-bit LFSR ==========
module lfsr32(
input clk,
input reset,
output reg [31:0] q
);
always @(posedge clk) begin
if (reset)
q <= 32'h1;
else begin
q <= {q[0]^1'b0, q[31:23], q[22]^q[0],
q[21:3], q[2]^q[0], q[1]^q[0]};
end
end
endmodule
// ========== 题目7: Shift register (m2014_q4k) ==========
module m2014_q4k(
input clk,
input resetn,
input in,
output reg out
);
reg [2:0] shift_reg;
always @(posedge clk) begin
if (!resetn) begin
shift_reg <= 3'b0;
out <= 0;
end else begin
shift_reg <= {in, shift_reg[2:1]};
out <= shift_reg[0];
end
end
endmodule
// ========== 题目8: Shift register (2014_q4b) ==========
module MUXDFF(
input clk,
input w, R, E, L,
output reg Q
);
// 第一级MUX:E选择w或Q
reg mux1;
always @(*) begin
if (E)
mux1 = w;
else
mux1 = Q;
end
// 第二级MUX:L选择R或mux1
reg mux2;
always @(*) begin
if (L)
mux2 = R;
else
mux2 = mux1;
end
// DFF:时钟上升沿更新
always @(posedge clk) begin
Q <= mux2;
end
endmodule
module top_module(
input [3:0] SW,
input [3:0] KEY,
output [3:0] LEDR
);
// 实例化4个MUXDFF,形成右移移位寄存器
// 注意:R的连接是SW[3]→LEDR[3], SW[2]→LEDR[2]...
MUXDFF MUXDFF_0(
.clk(KEY[0]),
.w(KEY[3]), // 最高位接收外部输入
.R(SW[3]), // 加载SW[3]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[3])
);
MUXDFF MUXDFF_1(
.clk(KEY[0]),
.w(LEDR[3]), // 从LEDR[3]接收
.R(SW[2]), // 加载SW[2]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[2])
);
MUXDFF MUXDFF_2(
.clk(KEY[0]),
.w(LEDR[2]), // 从LEDR[2]接收
.R(SW[1]), // 加载SW[1]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[1])
);
MUXDFF MUXDFF_3(
.clk(KEY[0]),
.w(LEDR[1]), // 从LEDR[1]接收
.R(SW[0]), // 加载SW[0]
.E(KEY[1]),
.L(KEY[2]),
.Q(LEDR[0])
);
endmodule
// ========== 题目9: 3-input LUT ==========
module ece241_2013_q12(
input clk,
input enable,
input S,
input A, B, C,
output reg Z
);
reg [7:0] q;
always @(posedge clk) begin
if (enable)
q <= {q[6:0], S};
end
assign Z = q[{A,B,C}];
endmodule
A2. 快速参考卡片
┌─────────────────────────────────────────┐
│ Shift Register Quick Reference │
├─────────────────────────────────────────┤
│ 右移: q <= q >> 1 │
│ q <= {1'b0, q[N-1:1]} │
│ │
│ 左移: q <= q << 1 │
│ q <= {q[N-2:0], 1'b0} │
│ │
│ 右循环: q <= {q[0], q[N-1:1]} │
│ 左循环: q <= {q[N-2:0], q[N-1]} │
│ │
│ 算术右移: q <= {q[N-1], q[N-1:1]} │
│ q <= q >>> 1 │
│ │
│ LFSR: 找本原多项式,复位到非0 │
└─────────────────────────────────────────┘
继续记录我的Verilog学习之路。如果你是路过的大佬,发现我哪里理解错了,请务必指出来!如果你也是正在入门的小伙伴,欢迎一起交流学习心得~




 浙公网安备 33010602011771号
浙公网安备 33010602011771号