完整教程：手写数字识别——单层神经网络

手写数字识别——单层神经网络（无 Sigmoid 版本）

• 1. 引言
• 2. 模型结构设计
• 3. 前向传播详解
• • • 3.1 线性变换（仿射映射）
    • 3.2 Softmax 归一化
• 4. 反向传播与梯度推导
• • • 4.1 损失函数定义
    • 4.2 关键梯度推导：$\frac{\partial \mathcal{L}}{\partial \mathbf{z}}$
    • 4.3 权重与偏置梯度
• 5. 与带 Sigmoid 版本的对比
• 6. 实验结果
• • 6.1 训练配置
  • 6.2 训练日志节选
  • 6.3 训练曲线
• 7. 全部代码
• 8. 总结
• 附：文章说明
• 参考文献

1. 引言

前文 MNIST 手写数字识别——单层神经网络 实现带 Sigmoid 激活的单层神经网络后，本文进一步优化模型结构，构建一个仅含线性层 + Softmax + 交叉熵损失的单层神经网络，完成对手写数字 MNIST 数据集¹的识别任务。

---

2. 模型结构设计

本文采用如下最简模型结构：

$$\begin{gathered} \mathbf{z}=\mathbf{XW}+\mathbf{b} \\ \mathbf{h}=\text{softmax}(\mathbf{z}) \\ \hat{y}=\arg \max (\mathbf{h}) \end{gathered}$$

其中：

• $\mathbf{X}\in {\mathbb{R}}^{N\times 784}$：输入数据，每行为一个展平的 28×28 手写图像（已归一化至 [0,1]）
• $\mathbf{W}\in {\mathbb{R}}^{784\times 10}$：可学习权重矩阵
• $\mathbf{b}\in {\mathbb{R}}^{1\times 10}$：偏置向量
• $\mathbf{z}\in {\mathbb{R}}^{N\times 10}$：线性输出（称为“logits”）
• $\mathbf{h}\in {\mathbb{R}}^{N\times 10}$：Softmax 后的概率分布，满足 ${\sum }_j{h}_{ij}=1$
• $\hat{y}\in \{0,1,\dots ,9\}$：预测类别

关键区别：与前一版本不同，此处省略了 Sigmoid 激活函数。模型直接对线性输出 $\mathbf{z}$ 应用 Softmax。这不仅简化了计算，还避免了 Sigmoid 带来的梯度饱和问题，同时使梯度推导更加简洁。

---

3. 前向传播详解

前向传播过程极为简洁，仅包含两个步骤：

3.1 线性变换（仿射映射）

$$\mathbf{z}=\mathbf{XW}+\mathbf{b}$$

• 每个样本 $x^{(i)}\in {\mathbb{R}}^{784}$ 被映射为 10 维 logits 向量 $z^{(i)}=W^{\top }{x}^{(i)}+b$
• 该变换是模型唯一的可学习部分

3.2 Softmax 归一化

$$h_j^{(i)}=\text{softmax}(z^{(i)}{)}_j=\frac{e^{z_j^{(i)}}}{{\sum }_{k=1}^{10}{e}^{z_k^{(i)}}},j=1,\dots ,10$$

• 将 logits 转换为概率分布
• 保证输出非负且和为 1，便于与 one-hot 标签比较

数值稳定性技巧：实际计算中，对每个样本的 logits 减去其最大值：
$${\tilde{z}}^{(i)}=z^{(i)}-\max (z^{(i)})$$
此操作不改变 Softmax 结果（因具有平移不变性），但能有效防止 $e^z$ 溢出。

---

4. 反向传播与梯度推导

Softmax 与交叉熵损失的组合具有极其简洁的梯度形式。

4.1 损失函数定义

交叉熵损失对单个样本 $i$ 定义为：
$$L^{(i)}=-\sum _{j=1}^{10}{y}_j^{(i)}\log h_j^{(i)}$$
其中 $y^{(i)}$ 是真实标签的 one-hot 编码（如标签为 3，则 $y^{(i)}=[0,0,0,1,0,\dots ,0]$）。

整体损失为批量平均：
$$\mathcal{L}=\frac{1}{N}\sum _{i=1}^N{L}^{(i)}$$

4.2 关键梯度推导：$\frac{\partial \mathcal{L}}{\partial \mathbf{z}}$

设 $\mathbf{Y}\in \{0,1{\}}^{N\times 10}$ 为 batch 的 one-hot 标签矩阵，$\mathbf{H}=\text{softmax}(\mathbf{Z})$ 为预测概率矩阵。

结论：
$$\frac{\partial \mathcal{L}}{\partial \mathbf{Z}}=\frac{1}{N}(\mathbf{H}-\mathbf{Y})$$

推导过程：

对单个样本 $i$，考虑第 $j$ 维输出：
$$\frac{\partial L^{(i)}}{\partial z_j^{(i)}}=\frac{\partial }{\partial z_j^{(i)}}\left(-\sum _k{y}_k^{(i)}\log h_k^{(i)}\right)=-\sum _k{y}_k^{(i)}\cdot \frac{1}{h_k^{(i)}}\cdot \frac{\partial h_k^{(i)}}{\partial z_j^{(i)}}$$

由 Softmax 导数性质：
$$\frac{\partial h_k^{(i)}}{\partial z_j^{(i)}}=\{\begin{array}{ll}{h}_j^{(i)}(1-h_j^{(i)}),& k=j\\ -h_k^{(i)}{h}_j^{(i)},& k\ne j\end{array}$$

代入并化简（利用 ${\sum }_k{y}_k^{(i)}=1$，且仅一个 $y_c^{(i)}=1$）：
$$\frac{\partial L^{(i)}}{\partial z_j^{(i)}}=h_j^{(i)}-y_j^{(i)}$$

因此，对整个 batch：
$$\frac{\partial \mathcal{L}}{\partial \mathbf{Z}}=\frac{1}{N}(\mathbf{H}-\mathbf{Y})$$

这一结果很重要：梯度直接等于“预测概率 - 真实标签”

4.3 权重与偏置梯度

由链式法则：
$$\frac{\partial \mathcal{L}}{\partial \mathbf{W}}={\mathbf{X}}^{\top }\cdot \frac{\partial \mathcal{L}}{\partial \mathbf{Z}}=\frac{1}{N}{\mathbf{X}}^{\top }(\mathbf{H}-\mathbf{Y})$$
$$\frac{\partial \mathcal{L}}{\partial \mathbf{b}}=\sum _{i=1}^N\frac{\partial L^{(i)}}{\partial \mathbf{b}}=\sum _{i=1}^N({\mathbf{h}}^{(i)}-{\mathbf{y}}^{(i)})={\frac{\partial \mathcal{L}}{\partial \mathbf{Z}}}^{\top }\cdot 1_N$$

在代码中，由于使用小批量（batch_size = $B$），梯度为：
$${\text{grad}}_W=\frac{1}{B}{X}_{\text{batch}}^{\top }(H_{\text{batch}}-Y_{\text{batch}})$$
$${\text{grad}}_b=\frac{1}{B}\sum _{i=1}^B(h^{(i)}-y^{(i)})$$

体现在代码中为：

grad_z = (y_pred - y_true_one_hot) / batch_size
grad_W = np.dot(X_batch.T, grad_z)
grad_b = np.sum(grad_z, axis=0, keepdims=True)

---

5. 与带 Sigmoid 版本的对比

项目	带 Sigmoid 版本	本文（无 Sigmoid）版本
模型结构	Linear → Sigmoid → Softmax	Linear → Softmax
最终性能	90.83%	92.34%

为何去掉 Sigmoid 反而效果更好？
Softmax 本身已是非线性激活函数，用于多分类输出。在 Softmax 前再加 Sigmoid 会导致输出被限制在 [0,1] 内，削弱 logits 的动态范围，反而降低模型表达能力。标准做法是直接对 logits 应用 Softmax。

---

6. 实验结果

6.1 训练配置

• Epochs: 100
• Learning rate: 0.1
• Batch size: 64
• 初始化: $W\sim \mathcal{N}(0,0.01^2)$

6.2 训练日志节选

Epoch 99/100 - val_loss: 0.2872 - val_accuracy: 0.9224
Epoch 100/100 - val_loss: 0.2876 - val_accuracy: 0.9210
Elapsed time: 26.14s
Final test accuracy: 0.9234, test loss: 0.2711

6.3 训练曲线

准确率曲线：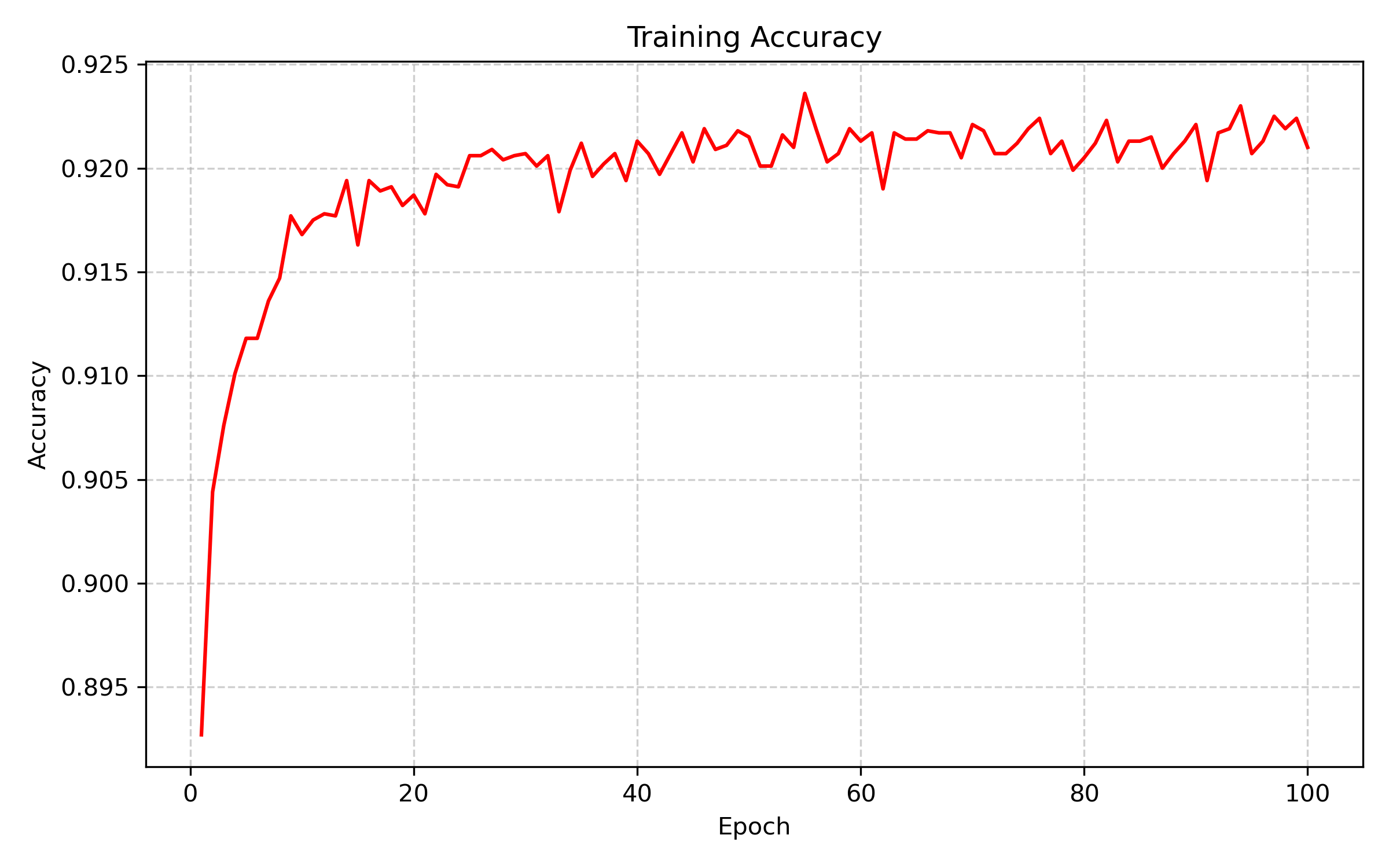

损失曲线：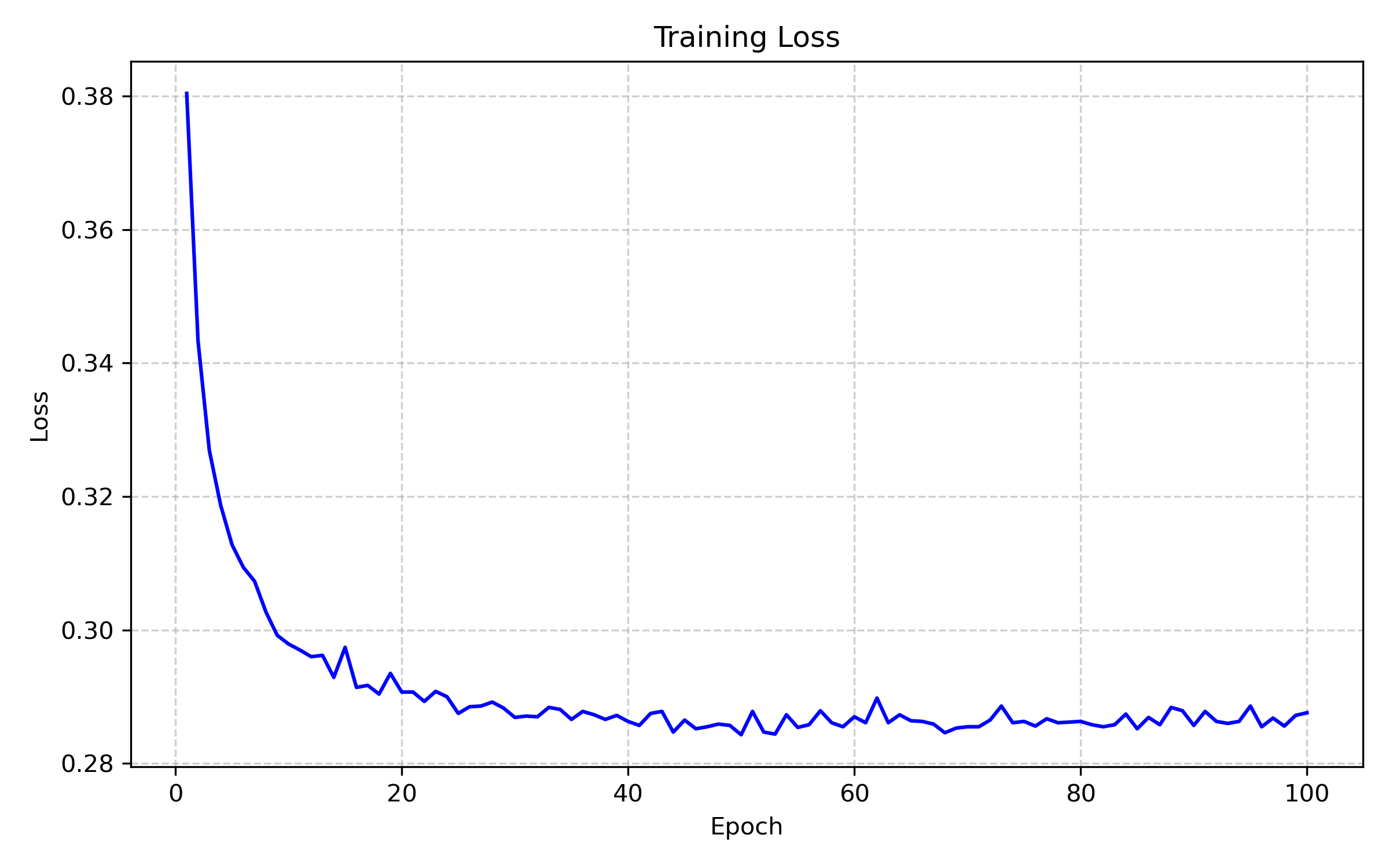

---

7. 全部代码

import os
import time
import pickle
import numpy as np
from sklearn.model_selection import train_test_split
def softmax(x):
"""带数值稳定性的 Softmax 函数"""
x_shifted = x - np.max(x, axis=1, keepdims=True)
exp_x = np.exp(x_shifted)
return exp_x / np.sum(exp_x, axis=1, keepdims=True)
def cross_entropy(y_pred, y_true, one_hot_matrix):
"""计算交叉熵损失"""
y_pred = np.clip(y_pred, 1e-15, 1.0)
y_true_one_hot = one_hot_matrix[y_true]
loss = -np.mean(np.sum(y_true_one_hot * np.log(y_pred), axis=1))
return loss
def load_mnist_data(train_path, test_path):
"""加载并预处理 MNIST 数据集"""
train_data = np.loadtxt(train_path, delimiter=',', skiprows=1)
test_data = np.loadtxt(test_path, delimiter=',', skiprows=1)
train_X = train_data[:, 1:] / 255.0
train_y = train_data[:, 0].astype(int)
test_X = test_data[:, 1:] / 255.0
test_y = test_data[:, 0].astype(int)
return train_X, train_y, test_X, test_y
def evaluate_model(X, y, W, b, one_hot_matrix):
"""在给定数据上评估模型：返回准确率和损失"""
z = np.dot(X, W) + b
probs = softmax(z)
preds = np.argmax(probs, axis=1)
accuracy = np.mean(preds == y)
loss = cross_entropy(probs, y, one_hot_matrix)
return accuracy, loss
def main():
# 文件路径配置
log_path = r'YOUR_LOG_DIR\mnist_simple_classifier_2.txt'
model_path = r'YOUR_MODEL_DIR\mnist_simple_classifier_best_model_2.pkl'
train_data_path = r'YOUR_DATA_DIR\mnist_train.csv'
test_data_path = r'YOUR_DATA_DIR\mnist_test.csv'
# 确保日志目录存在，并清空日志文件
os.makedirs(os.path.dirname(log_path), exist_ok=True)
with open(log_path, 'w', encoding='utf-8'):
pass
# 加载原始训练和测试数据
full_train_X, full_train_y, test_X, test_y = load_mnist_data(train_data_path, test_data_path)
# 划分训练集和验证集（80% train, 20% val）
train_X, val_X, train_y, val_y = train_test_split(
full_train_X, full_train_y,
test_size=0.2,
random_state=42,
stratify=full_train_y
)
# 初始化模型参数
input_dim = train_X.shape[1]  # 784
num_classes = 10
W = np.random.randn(input_dim, num_classes) * 0.01
b = np.zeros((1, num_classes))
# 预计算 one-hot 编码矩阵
one_hot_matrix = np.eye(num_classes)
# 超参数
learning_rate = 0.1
epochs = 100
batch_size = 64
# 跟踪最小验证损失
min_val_loss = float('inf')
start_time = time.perf_counter()
# 开始训练
for epoch in range(epochs):
# 打乱训练数据
indices = np.random.permutation(train_X.shape[0])
train_X = train_X[indices]
train_y = train_y[indices]
# 小批量训练
for i in range(0, train_X.shape[0], batch_size):
X_batch = train_X[i:i + batch_size]
y_batch = train_y[i:i + batch_size]
# 前向传播：线性 + softmax
z = np.dot(X_batch, W) + b
y_pred = softmax(z)
# 反向传播（Softmax + Cross-Entropy 的梯度）
y_true_one_hot = one_hot_matrix[y_batch]
grad_z = (y_pred - y_true_one_hot) / batch_size
grad_W = np.dot(X_batch.T, grad_z)
grad_b = np.sum(grad_z, axis=0, keepdims=True)
# 更新参数
W -= learning_rate * grad_W
b -= learning_rate * grad_b
# 每个 epoch 后在验证集上评估
val_acc, val_loss = evaluate_model(val_X, val_y, W, b, one_hot_matrix)
# 写入日志
log_line = f'Epoch {epoch + 1}/{epochs} - val_loss: {val_loss:.4f} - val_accuracy: {val_acc:.4f}'
with open(log_path, 'a', encoding='utf-8') as log:
log.write(log_line + '\n')
print(log_line)
# 保存验证损失最小的模型
if val_loss < min_val_loss:
min_val_loss = val_loss
best_model = {'w': W.copy(), 'b': b.copy()}
with open(model_path, 'wb') as f:
pickle.dump(best_model, f)
# 训练结束，加载最佳模型（基于最小验证损失）并在测试集上最终评估
with open(model_path, 'rb') as f:
best_model = pickle.load(f)
final_test_acc, final_test_loss = evaluate_model(test_X, test_y, best_model['w'], best_model['b'], one_hot_matrix)
elapsed = time.perf_counter() - start_time
print(f'\nElapsed time: {elapsed:.2f}s')
print(f'Final test accuracy: {final_test_acc:.4f}, test loss: {final_test_loss:.4f}')
# 将最终结果写入日志
with open(log_path, 'a', encoding='utf-8') as log:
log.write(f'\n[Best model selected by min val_loss = {min_val_loss:.4f}]\n')
log.write(f'Final test accuracy: {final_test_acc:.4f}\n')
if __name__ == '__main__':
main()

---

8. 总结

本文实现了一个无 Sigmoid 的单层神经网络。通过深入推导 Softmax 与交叉熵损失的梯度，我们发现：

1. 梯度形式极其简洁：${\nabla }_z\mathcal{L}=\frac{1}{N}(H-Y)$
2. 无需中间激活函数：Sigmoid 在此场景下是冗余的
3. 性能提升：准确率更高（90.83% vs 92.34%）

---

附：文章说明

本文仅为个人理解，仅做交流学习使用。若有不当之处，欢迎指正～

参考文献

---

1. LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. ↩︎