深入解析：SLAM文献之-Outlier-Robust Estimation: Hardness,Minimally Tuned Algorithms, and Applications(1)

摘要

机器人与计算机视觉中的非线性估计通常受到异常值困扰，这些异常值可能由错误的数据关联或信号处理与机器学习方法产生的错误检测引起。本文提出了两种统一的异常值鲁棒估计形式：广义最大一致性（Generalized Maximum Consensus, G-MC） 和 广义截断最小二乘（Generalized Truncated Least Squares, G-TLS），并研究了其基本极限、实用算法及应用。

本文的第一项贡献是证明异常值鲁棒估计不可逼近：在最坏情况下，即使运用比多项式时间更慢的算法（例如拟多项式时间算法），也无法（甚至近似地）找到异常值集合。

回顾并扩展两种通用算法。第一种算法就是第二项贡献Adaptive Trimming (ADAPT)为组合优化方法，适用于 G-MC；第二种算法Graduated Non-Convexity (GNC)基于同伦途径，适用于 G-TLS。我们将 ADAPT 和 GNC 扩展到用户不具备内点噪声统计知识（或噪声统计随时间变化）、并且无法猜测合理阈值以区分内点与异常值的情况（如 RANSAC 常用的阈值）。大家提出了首批最小调参算法（minimally tuned algorithms）来进行异常值剔除，这些算法能够动态决定如何区分内点和异常值。

第三项贡献是对所提出算法在机器人感知问题上的评估，包括：网格配准、基于图像的物体检测（形状对齐）以及位姿图优化。实验表明，ADAPT 和 GNC 可实时执行、具有确定性、性能优于 RANSAC，并能在高达 80–90% 异常值下保持鲁棒性。它们的最小调参版本同样优于现有技术，即便不依赖内点噪声的已知上限。

关键词：鲁棒估计、抗干扰感知、自主系统、计算机视觉、最大似然估计、算法、计算复杂性

---

I. 引言

现代感知系统（用于定位与建图）、物体姿态估计、运动估计与三维重建、形状分析、虚拟与增强现实以及医学成像等应用的核心支柱。就是非线性估计是机器人学与计算机视觉中的一个基础疑问，也

通过非线性估计能够被形式化为一个优化疑问，即寻找能够最好地解释观测测量值的估计结果。典型的感知流水线包括一个感知前端，用于从原始传感器材料（例如相机图像、激光雷达点云）中提取并匹配相关特征。这些潜在的特征匹配随后会传递到感知后端，利用非线性估计计算感兴趣的量（例如机器人的位置、外部物体的姿态）。在理想情况下，倘若所有特征匹配都是正确的，后端可以使用最小二乘形式进行估计：

$$\underset{x\in X}{\min }\sum _{i\in M}{r}^2(y_i,x)$$

其中，$x$是我们希望估计的变量（例如三维位姿），$X$是其定义域（例如所有位姿的集合），$M$是给定测量值的集合（例如属于某个物体的像素观测点），$y_i$ 是第 $i$ 个测量值，$r(y_i,x)\ge 0$ 是第 $i$个测量的残差，用于量化给定$x$ 与测量 $y_i$的拟合程度（例如线性标量测量时$r(y_i,x)=|y_i-a_i^{T}x|$）。当测量噪声服从高斯分布时，方程 (1) 的求解对应最大似然估计。然而，尽管形式上简单，该问题在全局上仍然难以求解，源于代价函数和定义域通常在机器人学应用中是非凸的。

在现实复杂环境下构建鲁棒的感知框架，要求设计抗异常值的估计方法。感知前端通常基于图像或信号处理办法，或者基于学习途径进行特征检测和匹配。然而，这些办法容易产生错误匹配，导致方程 (1) 中测量$y_i$完全错误，从而损害最终解的精度。在存在异常值的情况下计算鲁棒估计，一直是计算机视觉和机器人学中的核心问题。

对于低维估计挑战（例如基于图像或点云的物体姿态估计），研究者通常采用组合优化方法进行异常值剔除。特别地，一个流行的技巧是最大一致性（Maximum Consensus, MC）：寻找一个估计，使得尽可能多的测量值在给定的内点阈值$ϵ$内被解释（或等价地，最小化异常值数量）：

$$\underset{x\in X,O\subseteq M}{\min }|O|\text{s.t.}r(y_i,x)\le ϵ,\forall i\in M\setminus O$$

方程 (2) 中的 MC 疑问通常应用RANSAC 或 分支定界（Branch-and-Bound, BnB）非确定性的，需要最小求解器，并且仅适用于可以从少量测量计算估计的问题；BnB 在最坏情况下需要指数时间，难以扩展到大规模问题。就是方法求解。然而，RANSAC

对于高维估计问题（例如束调整、SLAM），研究者更多依赖M-估计来增强异常值鲁棒性。M-估计将方程 (1) 的最小二乘代价替换为对大残差不敏感的函数$\rho$：

$$\underset{x\in X}{\min }\sum _{i\in M}\rho (r(y_i,x),ϵ)$$

其中 $\rho$可以是 Huber、Cauchy 或 Geman-McClure 代价函数。M-估计的优势是得到一个连续优化问题（相比 MC 的组合优化），但由于代价函数和约束集通常非凸，全局求解仍然困难。机器人学应用中通常采用迭代局部求解器最小化 (3)，但局部求解器依赖良好的初始值（在应用中通常不可得）且容易陷入局部最优，得到不理想的估计。

总的来说，目前文献中缺少一种方法能够同时满足以下条件：

1. 高速且可扩展到大规模问题
2. 确定性
3. 无需初始估计

这种缺口导致现代感知框架在安全关键应用中脆弱，限制了感知在自动驾驶、无人机和航天器等领域的使用。

此外，现有鲁棒估计算法还依赖对期望（内点）测量噪声的已知信息，这在方程 (2) 和 (3) 中由参数$ϵ$表示。然而，很多问题中，准确标定该参数既耗时又繁琐（如需要在受控环境中收集数据），或依赖人工调参。这种方法也不适合长期操作，例如地面机器人进行长期 SLAM，噪声统计可能随时间变化（如轮胎漏气导致里程计噪声增加），使得工厂标定失效。

---

本文贡献

本文针对上述困难，从计算极限与算法设计两个方面提出了贡献：

1. 通用建模与不可逼近性分析

   • 提出两种统一的异常值鲁棒估计形式：广义最大一致性（G-MC） 和 广义截断最小二乘（G-TLS）。
   • G-MC 是组合优化形式，推广了传统 MC 和最小修剪平方（MTS）；G-TLS 是连续优化形式，推广了 M-估计中的截断最小二乘方法。
   • 给予概率解释：G-MC 可视作受似然约束的估计，G-TLS 是最大似然估计。
   • 献出必要与充分条件保证两者返回同解，但条件一般不满足，且 G-TLS 能剔除更多测量，但可能得到更精确的估计。
   • 证明 G-MC 和 G-TLS 即使使用拟多项式算法也不可逼近，反映其计算困难性。

2. 通用且最小调参算法

   • 提出两类通用算法：组合优化技巧ADAPT（适用于 G-MC）和连续优化方法GNC（适用于 G-TLS）。
   • 两者线性复杂度、确定性、无需初始估计。
   • 提出 ADAPT-MinT 和 GNC-MinT，能够自动调节参数进行鲁棒估计，无需先验内点噪声知识。

3. 机器人与视觉应用实验

   • 在网格配准、基于图像的物体检测（形状对齐）、位姿图优化三个任务上测试算法。
   • 在网格配准和形状对齐中，ADAPT 与 GNC 实时运行，性能优于 RANSAC，并能处理高达 80% 异常值。
   • 在位姿图优化中，ADAPT 与 GNC 优于局部优化和临时技术，可处理高达 90% 异常值。
   • 最小调参版本性能接近 ADAPT 与 GNC，但无需内点噪声上限知识。

---

与既有工作差异

• 本文扩展了 ADAPT 和 GNC 方法，并提出 G-MC 与 G-TLS 新形式，首次提供概率解释及关系分析。
• 提供 ADAPT 局部收敛性证明。
• 最小调参算法（ADAPT-MinT 与 GNC-MinT）为全新贡献。
• 实验覆盖 3D SLAM 问题，并补充了文献综述和手艺证明，说明贪心算法对异常值剔除的局限性。

---

II. 鲁棒估计：广义最大一致性与广义截断最小二乘

本节介绍**广义最大一致性（Generalized Maximum Consensus, G-MC）和广义截断最小二乘（Generalized Truncated Least Squares, G-TLS）**两种鲁棒估计框架。

• 第 II-A、II-B 节：提出 G-MC 和 G-TLS 的一般形式；
• 第 II-C 节：从概率角度对 G-MC 与 G-TLS 进行解释（命题 2–4）；
• 第 II-D 节：给出 G-MC 与 G-TLS 等价的条件（定理 7）。

我们使用以下记号：

• $x^{\circ }$：为要估计的真实变量值；
• $O^{\circ }$：为真实的离群点集合；
• 对任意 $I\subseteq M$，定义 $r(y_I,x)=[r(y_i,x){]}_{i\in I}$，即测量集合$i\in I$的残差向量。

---

A. 广义最大一致性（Generalized Maximum Consensus, G-MC）

我们第一给出广义最大一致性疑问的定义。

问题 1（G-MC）
求估计量 $x$，使得组合优化障碍成立：
$$\underset{x\in \mathcal{X},O\subseteq M}{\min }|O|\text{s.t.}|r(y_{M\setminus O},x)|\ast \ell \le \tau ,\text{\hspace{1em}(G-MC)}$$
其中 $\tau \ge 0$为给定的内点阈值，$|\cdot |\ast \ell$表示一般的向量范数（本文中$\ell \in 2,\infty$）。

由于离群点数量未知，G-MC 的思想是拒绝尽可能少的测量值，使剩余测量表现为内点。
其中：

• $O$表示被判定为离群点的测量集合；
• $M\setminus O$表示被视为内点的集合；
• 当存在某个 $x$，使得内点残差的累积误差$|r(y_{M\setminus O},x){|}_{\ell }$ 小于阈值 $\tau$ 时，组合 $M\setminus O$ 被认为是可行的。

G-MC 泛化了以往的多种离群点剔除方法。具体地，依赖于范数$\ell$ 与阈值 $\tau$的选择，G-MC 可退化为以下形式：

• 当 $\ell =\infty ,\tau =ϵ$ 时，G-MC 等价于最大一致性（MC）：
  $$|r(y_{M\setminus O},x){|}_{\infty }\le ϵ\Rightarrow |r(y_i,x)|\le ϵ,\forall i\in M\setminus O.$$

• 当 $\ell =2$ 时，G-MC 等价于最小截断平方（MTS）：
  $$\underset{x\in \mathcal{X},O\subseteq M}{\min }|O|\text{s.t.}\sum _{i\in M\setminus O}{r}^2(y_i,x)\le {\tau }^2.\text{\hspace{1em}(4)}$$

---

B. 广义截断最小二乘（Generalized Truncated Least Squares, G-TLS）

接着，我们提出广义截断最小二乘的定义，这是一种对 M-估计（M-estimation）中 TLS 的推广。

问题 2（G-TLS）
求估计量 $x$，解如下优化问题：
$$\underset{x\in \mathcal{X},O\subseteq M}{\min }{\nu }_{\ell }(O),|r(y_{M\setminus O},x)|\ast {\ell }^2+{ϵ}^2|O|,\text{\hspace{1em}(G-TLS)}$$
其中 $|\cdot |\ast \ell$为一般向量范数（$\ell \in 2,\infty$），
${\nu }_{\ell }(O)$、$ϵ>0$为给定的惩罚系数。
其中专门地：${\nu }_2(O)=1,{\nu }_{\infty }(O)=|M\setminus O|$。

G-TLS 通过分离内点与外点，寻求鲁棒的$x$ 估计：

• 内点残差以 ${\nu }_{\ell }(O),|r(y_{M\setminus O},x){|}_{\ell }^2$ 加权惩罚；
• 外点数量以 ${ϵ}^2|O|$ 加权惩罚。

当参数取特定值时，G-TLS 可退化为经典形式：

• 当 $\ell =2$ 时，G-TLS 变为：
  $$\underset{x,O}{\min }\sum _{i\in M\setminus O}{r}^2(y_i,x)+\sum _{i\in O}{ϵ}^2,\text{\hspace{1em}(5)}$$
  等价于经典的截断最小二乘（TLS）：
  $$\underset{x\in \mathcal{X}}{\min }\sum _{i\in M}\underset{w_i\in 0,1}{\min }\left[w_i{r}^2(y_i,x)+(1-w_i){ϵ}^2\right].\text{\hspace{1em}(TLS)}$$

• 当 $\ell =2,ϵ=+\infty$时，G-TLS 退化为标准最小二乘（LS）模型。

---

C. G-MC 与 G-TLS 的概率解释

大家给出两种广义鲁棒估计模型的概率基础，假设各测量噪声相互独立。

假设 1（独立噪声）
对于任意 $i\ne j,i,j\in M$，
残差 $r(y_i,x)$ 与 $r(y_j,x)$是相互独立的随机变量。

以下命题说明了在不同的分布假设下，G-MC 与 G-TLS 的概率意义。

---

命题 2（均匀分布的内点 → MC）

若对任意 $i\in M\setminus O^{\circ }$，
$$r(y_i,x^{\circ })\sim \text{Uniform}(0,ϵ),$$
则最大一致性（MC）可写为：
$$\underset{x,O}{\min }|O|\text{s.t.}\prod _{i\in M\setminus O}u(r(y_i,x),ϵ)>0,\text{\hspace{1em}(6)}$$
其中 $u(r,ϵ)$ 为区间 $[0,ϵ)$上的均匀分布概率密度函数。

因此，MC 等价于：寻找一个 $x$，使得所有内点的联合似然大于 0。

---

命题 3（正态分布的内点 → MTS）

若对任意 $i\in M\setminus O^{\circ }$，
$$r(y_i,x^{\circ })\sim \mathcal{N}(0,1),$$
则最小截断平方（MTS）等价于：
$$\underset{x,O}{\min }|O|\text{s.t.}\prod _{i\in M\setminus O}g(r(y_i,x))\ge e^{-{\tau }^2/2}{\left(\frac{\pi }{2}\right)}^{|M\setminus O|/2},\text{\hspace{1em}(7)}$$
其中 $g(r)=\sqrt{\frac{2}{\pi }}{e}^{-r^2/2}$，为限制在非负轴上的正态分布密度函数。

命题 3 表明，MTS 相当于假设内点服从正态分布下的似然约束估计。

---

接下来我们展示 G-TLS（独特是 TLS）的概率解释。若离群点数量已知，可将 TLS 视为最大似然估计器；若离群点数量未知，则可解释为混合分布（正态 + 均匀）模型。

命题 4（已知离群点数、正态分布 → TLS）

若对任意 $i\in M\setminus O^{\circ }$，
$r(y_i,x^{\circ })$服从正态分布，且$|O^{\circ }|$ 已知，
并且 $r(y_i,x^{\circ })<ϵ$，则 TLS 等价于：
$$\underset{x,O\subseteq M,|O|=|O^{\circ }|}{\max }\prod _{i\in M\setminus O}g(r(y_i,x)).\text{\hspace{1em}(8)}$$

---

命题 5（正态分布 + 均匀尾部 → TLS）

假设对任意 $i\in M$：

1. $r(y_i,x^{\circ })\le \alpha$；
2. $r(y_i,x^{\circ })$服从修改后的正态分布：
   $$\hat{g}(r)=\frac{1}{\beta }\{\begin{array}{llcc}g(r),& r<ϵ,g(ϵ),& r\in [ϵ,\alpha ],0,& \text{otherwise,}\end{array}\text{\hspace{1em}(9)}$$
   其中 $\beta$为归一化因子，使得${\int }_0^{\alpha }\hat{g}(r),dr=1$。

则 TLS 等价于最大似然估计：
$$\underset{x\in \mathcal{X}}{\max }\prod _{i\in M}\hat{g}(r(y_i,x)).\text{\hspace{1em}(10)}$$

在附录 3 中，TLS 还被解释为：在测量点被错误分类（将离群点当作内点或相反）的情况下，最小化估计误差概率，该概率可用 Weibull 分布的乘积表示。

---

D. G-MC 与 G-TLS 的关系

定理 6（当$\ell =\infty$时 G-MC = G-TLS）

当在 G-MC 与 G-TLS 中选择$|\cdot |\ast \ell =|\cdot |\ast \infty$，并令 $\tau =ϵ$，
若 G-MC 的最优解$(x_{G\text{-MC}},O_{G\text{-MC}})$ 满足：
$$|r(y_{M\setminus O_{G\text{-MC}}},x_{G\text{-MC}}){|}_{\infty }<ϵ,$$
则 G-MC 与 G-TLS 计算出的离群点集合相同。

由于测量数据为随机变量，上述不等式严格成立的概率为 1，因此在$\ell =\infty$ 的情况下，G-MC 与 G-TLS 等价的概率为 1。因此，后续仅关注$\ell =2$的情形（即 TLS）。

---

定理 7（当$\ell =2$时 G-MC 与 G-TLS 的关系）

定义：

• $(x_{\text{MTS}},O_{\text{MTS}})$：为 MTS 的最优解（即 G-MC 在$\ell =2$下的特例）；
• $(x_{\text{TLS}},O_{\text{TLS}})$：为 TLS 的最优解（即 G-TLS 在$\ell =2$、${\nu }_{\ell }(O)=1$下的特例）；
• $r_{\text{TLS}}^2(ϵ)=|r(y_{M\setminus O_{\text{TLS}}},x_{\text{TLS}}){|}_2^2$：内点残差平方和；
• $f_{\text{TLS}}(ϵ)=r_{\text{TLS}}^2(ϵ)+{ϵ}^2|O_{\text{TLS}}|$：TLS 的目标函数值。

则对任意 $ϵ>0$：

1. 若 $\tau =r_{\text{TLS}}(ϵ)$，则 $|O_{\text{TLS}}|=|O_{\text{MTS}}|$，且 $(x_{\text{TLS}},O_{\text{TLS}})$也是 MTS 的解；
2. 若 $\tau >r_{\text{TLS}}(ϵ)$，则 $|O_{\text{TLS}}|\ge |O_{\text{MTS}}|$；
3. 若 $\tau <r_{\text{TLS}}(ϵ)$，则 $|O_{\text{TLS}}|<|O_{\text{MTS}}|$，此时两者计算出的离群点集合不同。

---

例 8（有时少即是多）

考虑一个容易估计挑战：

• 真实变量 $x^{\circ }=0$；
• 三个测量：$y_1=y_2=0$（内点），$y_3=4$（外点）；
• 测量模型 $y_i=x+n_i,i=1,2,3$，其中 $n_i$为零均值单位方差高斯噪声。

设：

• TLS 中 $ϵ=2.58$，保证 $|n_i|\le ϵ$的概率约为 0.99；
• MTS 中 $\tau =11.35$，保证 $n_1^2+n_2^2+n_3^2\le \tau$的概率约为 0.99。

显然在真实值$x^{\circ }=0$ 时：
$$r(y_1,x^{\circ })=r(y_2,x^{\circ })=0,r(y_3,x^{\circ })=4.$$

在此情形下：

• MTS误判所有点为内点并给出错误估计：
  $$x=\frac{4}{3},r^2(y_1,x)+r^2(y_2,x)+r^2(y_3,x)=\frac{32}{3}\approx 10.67<\tau .$$
  因此 MTS 接受了所有测量（包括离群点）。

• TLS虽然剔除了更多测量（排除了第 3 个测量），却给出了正确估计$x=0$。

该例说明：TLS 可能拒绝更多测量，但能得到更准确的估计结果，因为它倾向于排除偏差较大的测量。

（TLS 与 MC 的更详细比较见 [4, Appendix C]。）

---

总结要点

模型	范数选择	等价形式	假设分布	主要思想
G-MC	$\ell \in 2,\infty$	MC / MTS	均匀或正态	约束似然、最少拒绝点
G-TLS	$\ell \in 2,\infty$	TLS / LS	混合分布	平衡残差与拒绝代价
等价性	当 $\ell =\infty$ 或特殊阈值	G-MC ≡ G-TLS	-	两者统一在似然约束框架内

---

III. G-MC 与 G-TLS 的不可近似性

本节说明 G-MC 与 G-TLS 在计算上是难以求解的，尤其是在最坏情况下，即便是准多项式时间算法也难以对它们的解进行有效近似。

我们先回顾计算复杂度理论中的$O(\cdot )$ 与 $\Omega (\cdot )$符号 [26]。

---

定义 9（O 符号）

设 $h:\mathbb{N}\to \mathbb{R}$ 和 $g:\mathbb{N}\to \mathbb{R}$。
若存在常数 $k>0$，使得当 $m$ 足够大时：
$$h(m)\le kg(m),$$
则记作 $h(m)=O(g(m))$。

---

定义 10（$\Omega$ 符号）

设 $h:\mathbb{N}\to \mathbb{R}$ 和 $g:\mathbb{N}\to \mathbb{R}$。
若存在常数 $k>0$，使得当 $m$ 足够大时：
$$h(m)\ge kg(m),$$
则记作 $h(m)=\Omega (g(m))$。

---

定义 11（$(\lambda ,p)$-可近似性）

设 $\lambda \ge 1$，$p\ge 0$。

• G-MC 称为$(\lambda ,p)$-可近似，若是存在一个算法可以找到 G-MC 的次优解$(x,O)$，使得：
  $$|O|\le \lambda |O_{G-\text{MC}}|,|r(y_{M\setminus O},x)|\ast {\ell }^2\le |r(y\ast M\setminus O_{G-\text{MC}},x_{G-\text{MC}})|\ast {\ell }^2+p,$$
  其中 $(x\ast G-\text{MC},O_{G-\text{MC}})$为 G-MC 的最优解。

• 同理，G-TLS 称为$(\lambda ,p)$-可近似，假如存在算法找到次优解$(x,O)$ 使得：
  $$|O|\le \lambda |O_{G-\text{TLS}}|,|r(y_{M\setminus O},x)|\ast {\ell }^2\le |r(y\ast M\setminus O_{G-\text{TLS}},x_{G-\text{TLS}})|\ast {\ell }^2+p,$$
  其中 $(x\ast G-\text{TLS},O_{G-\text{TLS}})$为 G-TLS 的最优解。

解释：定义 11 限制了近似解的次优程度。若$(x,O)$ 为 $(\lambda ,p)$-近似解，则：

1. $O$拒绝的离群点最多是最优解集合的$\lambda$ 倍；
2. 内点残差误差最多比最优解多$p$。

---

定理 12（G-MC 与 G-TLS 的不可近似性）

对任意 $\delta \in (0,1)$，除非 $NP\subseteq BPTIME(|M{|}^{\text{poly log}|M|})$，否则存在：

• $\lambda (|M|)=2^{\Omega ({\log }^{1-\delta }|M|)}$，
• 多项式函数 $p(|M|)$，
• 以及 G-MC 的实例，使得任何准多项式时间算法都无法使这些实例达到$(\lambda (|M|),p(|M|))$-可近似。

该结论即便在算法已知：

1. $|O_{G-\text{MC}}|$（最优离群点数），以及
2. 最优解满足 $|r(y_{M\setminus O_{G-\text{MC}}},x_{G-\text{MC}}){|}_{\ell }^2=0$

的情况下仍然成立。

同理，对于 G-TLS 也成立，即便算法已知：

1. $|O_{G-\text{TLS}}|$，以及
2. 最优解残差为零：$|r(y_{M\setminus O_{G-\text{TLS}}},x_{G-\text{TLS}}){|}_{\ell }^2=0$。

---

含义与解读

该定理体现了 G-MC 与 G-TLS 的极端困难性：

• 在最坏情况下，任何准多项式时间算法都无法在 $(\lambda ,p)$-意义下近似求解 G-MC 或 G-TLS；
• 甚至当算法已知最优的离群点数或最优残差为零时，结论仍成立；
• 近似质量依赖于定理 12 中的$\lambda$ 与 $p$，它们都随测量数量$|M|$增长；特别地，$\lambda$ 随 $|M|$指数增长（当$\delta \to 0$ 时，$\lambda \propto |M|$）；
• 因此，定理表明不存在准多项式时间算法能够为 G-MC 或 G-TLS 提供常数次优界。

该结论也强化了针对最大一致性（MC）的最近不可近似性结果，而这些结果仅关注多项式时间算法 [15]。

---

IV. 自适应裁剪（ADAPT）算法

我们提出 ADAPT，一种通用的、确定性的、线性时间算法，用于求解 G-MC，无需初始估计。

首先在 IV-A节介绍一个简单的贪心算法以建立直觉，然后在IV-B节引入 ADAPT。

---

A. 常规应用：贪心离群点剔除

我们先描述一个用于 G-MC 的简单贪心算法，以建立对 ADAPT 的直觉。

该算法从对整个测量集合求解类似于公式 (1) 的最小二乘障碍开始，并在每次迭代中剔除残差最大的测量。算法在满足 (G-MC) 中条件$|r(y_{M\setminus O},x){|}_{\ell }\le \tau$ 时停止。

虽然该贪心算法因其方便性和线性运行时间而具有吸引力，但存在两个问题：

1. 无法纠正过去的错误：一旦某个测量被剔除，它就不会被重新考虑；
2. 终止条件有限：算法在达到阈值$\tau$后停止，但并未检查是否所有离群点都已剔除，例如通过观察$|r(y_{M\setminus O},x){|}_2$ 是否收敛。

因此，该算法在某些情况下性能可能下降（参见第 VII-C 节的 SLAM 实验）。

---

B. 高级应用：ADAPT 算法

我们提出 自适应裁剪（ADAPT）算法来求解问题 1 中的 G-MC。

• 算法在每次迭代中处理所有测量，并剔除超过内点阈值的测量（阈值在每次迭代中自适应下降）。
• 算法的自适应性在于每次迭代动态决定阈值。
• ADAPT 并非贪心算法：它可以纠正之前的错误，即某次迭代被判定为离群点的测量可以在后续迭代中重新成为内点，反之亦然。
• ADAPT 还会借助检查$|r(y_{M\setminus O},x){|}_2$否所有离群点已被剔除。就是的收敛性来评估
• 与贪心算法每次仅剔除一个测量不同，ADAPT 可在每次迭代中剔除多个测量。
• 算法伪代码见算法 1。
  

---

初始化

1. 内点集合初始化：将假定内点集合设置为$I^{(0)}=M$（所有测量）；
2. 对于后续迭代$t=1,2,\dots$，集合 $I^{(t)}$ 仅包含在第 $t$次迭代中被分类为内点的测量；
3. 计算初始估计：
   $$x^{(0)}=\arg \underset{x\in X}{\min }|r(y_{I^{(0)}},x){|}_2^2,$$
   即假设所有测量都是内点时的估计。非最小解的非线性最小二乘问题可用非最小求解器求解 [27]。
4. 初始内点阈值：
   $${ϵ}^{(0)}=\text{ThrDiscount}\cdot \underset{i\in I^{(0)}}{\max }r(y_i,x^{(0)}),$$
   其中 ThrDiscount$<1$是一个乘法因子（本文固定为 0.99），确保至少一个测量在下一次迭代被判定为离群点。

---

主循环

ADAPT 的主循环开始离群点剔除（line 3），步骤如下：

a) 内点集合更新

• 在第 $t$次迭代，给定${ϵ}^{(t-1)}$，更新内点集合：
  $$I^{(t)}=i\in M\mid r(y_i,x^{(t-1)})<{ϵ}^{(t-1)}.$$
• 由于 ADAPT 检查所有测量，$I^{(t)}$可能包含先前被剔除的测量，也可能剔除先前被纳入的测量。
• $I^{(t)}$依赖于历史序列$(I^{(1)},\dots ,I^{(t-1)})$，因为 ${ϵ}^{(t-1)}$ 依赖于 $I^{(t-1)}$。
• 迭代过程中，序列$((I^{(1)},{ϵ}^{(1)}),\dots ,(I^{(t)},{ϵ}^{(t)}),\dots )$会逐步生成，即便初期分类有误，最终测量也能正确分类。

b) 变量更新

• 给定 $I^{(t)}$，计算新的估计$x^{(t)}$（line 5）。
• 该步骤仍为非最小二乘问题，可用非最小求解器求解 [27]。

c) 内点阈值更新

• 若当前估计对 G-MC 不可行，或$|r(y_{M\setminus O},x){|}_2$在 SamplesToConverg 次迭代内未收敛，则更新${ϵ}^{(t)}$（line 15），并进行下一次迭代。
• 阈值更新同初始化，通过乘以 ThrDiscount$<1$，使至少一个测量被剔除。

---

终止条件

ADAPT 在以下情况下终止：

1. 达到最大迭代次数（本文设置 MaxIterations = 1000）；
2. 找到 G-MC 的可行估计，并且在 SamplesToConverg 次迭代中$|r(y_{M\setminus O},x){|}_2$ 变化不超过 $\theta$（本文设置 SamplesToConverg = 3）。

终止后，返回当前估计$x^{(t)}$ 和内点集合 $I^{(t)}$（line 17）。

---

备注

Remark 13（线性运行时间）

• ADAPT 更新${ϵ}^{(t)}$ 的策略保证 $|I^{(t)}|\le |I^{(t-1)}|-1$，因此 ADAPT 最多在$|M|$次迭代内终止。

Remark 14（与 RANSAC 对比）

• RANSAC 是随机算法，ADAPT 是确定性算法；
• RANSAC 仅维持测量集的“局部视图”，通过最小测量集采样构建内点集；而 ADAPT 检查所有测量以选择内点集；
• RANSAC 依赖最小求解器，ADAPT 依赖非最小求解器；
• RANSAC 不适合高维问题，因为采样到无离群点集合的迭代次数随问题维度指数增长；ADAPT 则为线性时间，迭代次数最多等于测量数量。

---

V. 分阶段非凸性（GNC）算法

我们简要回顾在先前工作 [27] 中提出的GNC通过算法。我们展示了——在考虑 TLS 代价时——该算法可能在不使用 Black-Rangarajan 对偶的情况下简单解释。此外，我们给出一个新的局部收敛结果（下文定理 15），从而能够为算法给予更简单的终止条件。

我们将在 V-A节简要回顾分阶段非凸性概念，并在V-B节描述 GNC 算法。

---

A. 分阶段非凸性的预备知识

在介绍 GNC 算法前，我们回顾分阶段非凸性（Graduated Non-Convexity, GNC）的概念 [19, 27, 35, 36]。

求解 TLS 问题（已在公式 (TLS) 中引入）：就是本节目标
$$\underset{x\in X}{\min }\sum _{i\in M}\underset{w_i\in 0,1}{\min }[w_i{r}^2(y_i,x)+(1-w_i){ϵ}^2].\text{\hspace{1em}(11)}$$

求解公式 (11) 极其困难，因为 TLS 目标函数在残差$r$上高度非凸。实际上，公式 (11) 中的第$i$ 项：
$$\underset{w_i\in 0,1}{\min }[w_i{r}^2(y_i,x)+(1-w_i){ϵ}^2]$$
描述了一个截断二次函数，其非凸性如图 2(a) 所示。

分阶段非凸性通过同伦法（homotopy 或 continuation method）[36] 避免了这种非凸性。具体来说，GNC 通过用一个由参数$\mu$控制的代理函数“软化” TLS 的非凸性：
$$\underset{x\in X}{\min }\sum _{i\in M}\underset{w_i\in [0,1]}{\min }[w_i{r}^2(y_i,x)+\frac{\mu (1-w_i)}{\mu +w_i}{ϵ}^2].\text{\hspace{1em}(12)}$$

• 公式 (11) 中的正则项$(1-w_i){ϵ}^2$ 被替换为 $\mu (1-w_i){ϵ}^2/(\mu +w_i)$。
• 当 $\mu \to 0$时，公式 (12) 成为凸优化问题 [27]；
• 当 $\mu \to +\infty$ 时，$\mu (1-w_i){ϵ}^2/(\mu +w_i)\to (1-w_i){ϵ}^2$，即公式 (12) 恢复原始 TLS。

公式 (12) 中参数$\mu$所对应的代理函数族如图 2(b) 所示。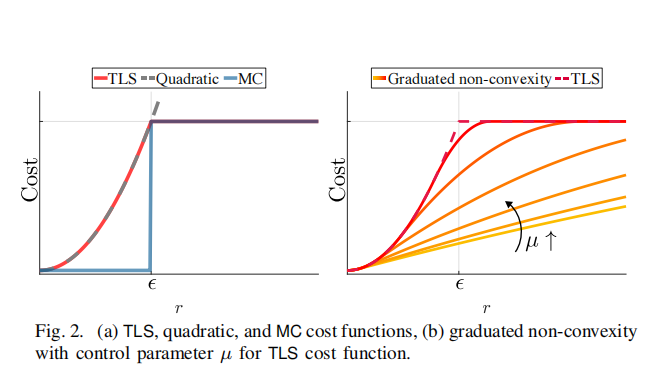

GNC 利用从小$\mu$开始求解 TLS 的凸近似，然后逐步增加$\mu$以恢复原始 TLS 的非凸性。每次迭代得到的估计用作下一次迭代的初始值，以降低陷入局部最小值的风险。

---

B. GNC-TLS 算法

GNC-TLS的伪代码见算法 2。

除了利用分阶段非凸性之外，每次迭代，GNC-TLS 通过交替优化$x$（固定 $w_i$）和 $w_i$（固定 $x$）来最小化公式 (12) 的代理函数。两步优化都可以高效求解。

---

初始化

1. 参数 $\mu$初始化为较小数值 [27]（line 1）；
2. 所有权重初始化为 1（即$w^{(0)}=1\ast M$，长度为 $|M|$的全 1 向量），并将$x$初始化为最小二乘解：
   $$x^{(0)}=\arg \min \ast x\in X\sum _{i\in M}{r}^2(y_i,x).\text{\hspace{1em}(13)}$$
   算法中记为 VariableUpdate(w0)。

---

主循环

初始化后，GNC-TLS 开始主要的离群点剔除循环（line 3）。

在第 $t$ 次迭代中：

1. 权重更新（line 4）：固定$x^{(t-1)}$ 和 ${\mu }^{(t-1)}$，更新权重 $w^{(t)}$：
   $$w^{(t)}=\arg \underset{w_i\in [0,1]}{\min }\sum _{i\in M}[w_i{r}_i^{(t)}+\frac{{\mu }^{(t-1)}(1-w_i)}{{\mu }^{(t-1)}+w_i}{ϵ}^2],\text{\hspace{1em}(14)}$$
   其中 $r_i^{(t)}=r(y_i,x^{(t)})$。
   该公式可分解为$|M|$个标量问题，并可用闭式解求解 [27]：
   $$w_i^{(t)}=\{\begin{array}{llcc}1,& r_i^{(t)}<ϵ\sqrt{\frac{{\mu }^{(t-1)}}{{\mu }^{(t-1)}+1}}0,& r_i^{(t)}>ϵ\sqrt{\frac{{\mu }^{(t-1)}+1}{{\mu }^{(t-1)}}}\frac{\sqrt{{\mu }^{(t-1)}({\mu }^{(t-1)}+1)}{r}_i^{(t)}-{\mu }^{(t-1)}}{\dots },& \text{otherwise.}\end{array}\text{\hspace{1em}(15)}$$

2. 变量更新（line 5）：固定$w^{(t)}$，更新 $x^{(t)}$：
   $$x^{(t)}=\arg \underset{x\in X}{\min }\sum _{i\in M}{w}_i^{(t)}{r}^2(y_i,x).\text{\hspace{1em}(16)}$$
   这是加权最小二乘困难，可用非最小求解器全局最优求解 [27]。

3. 增加非凸性：$\mu$ 更新（line 6）：每次迭代结束后，$\mu$乘以一个因子 MuUpdateFactor$>1$（本文取 1.4），逐步逼近原始 TLS 非凸代价。

---

终止条件

GNC-TLS 在以下情况下终止：

1. 达到最大迭代次数（本文 MaxIterations = 1000）；
2. 权重向量 $w^{(t)}$变为二进制向量（line 7）。

定理 15 给出了该条件的理论协助：

定理 15（权重向二进制向量收敛的概率为 1）
若 $t\to +\infty$，则
$$w_i^{(t)}\to w_i^{(\infty )}=\{\begin{array}{llcc}1,& r_i^{(\infty )}<ϵ0,& r_i^{(\infty )}>ϵ1/2,& r_i^{(\infty )}=ϵ\end{array}\text{\hspace{1em}(17)}$$
由于测量受到随机噪声影响，$r_i^{(\infty )}=ϵ$的概率为零。

公式 (17) 与 TLS 公式 (11) 一致：当测量$i$被视为内点时$w_i^{(\infty )}=1$，否则 $w_i^{(\infty )}=0$。

---

VI. 最小调参的 ADAPT 与 GNC：ADAPT-MinT 与 GNC-MinT

---

A. ADAPT-MinT 算法

ADAPT-MinT与 ADAPT 类似，但引入了一种无需内点阈值的终止条件。
与依赖给定 $\tau$（区分内点和离群点）而终止的 ADAPT 不同，ADAPT-MinT：

1. 根据当前估计$x^{(t)}$查看所有测量的残差；
2. 将残差聚类为两组：低幅值残差的“内点”组（图 3 左侧）和高幅值残差的“离群点”组（图 3 右侧）；
3. 当两组的“质心距离”($\delta$) 收敛到稳定状态时终止。
   

为了将所有残差分为两组，并计算质心及质心间距离，ADAPT-MinT 调用附录 6（算法 5）中的子程序 ClustersSeparation。

伪代码见算法 3。

---

初始化

• 行 1-2 与 ADAPT 相同，初始化$I^{(0)}$ 和 $x^{(0)}$；
• 行 3 新增：根据$x^{(0)}$ 初始化 ${\delta }^{(0)}$，即内点与离群点质心之间的初始距离。
• 后续迭代 $t=1,2,\dots$ 中，${\delta }^{(0)}$ 用作 ${\delta }^{(t)}$的归一化因子（line 8）。

---

内点集合、变量与阈值更新

• 行 5、6、7 与 ADAPT 相同，用于更新内点集合、变量和内点阈值。

---

内点/离群点聚类分离更新

• ADAPT-MinT 更新${\delta }^{(t)}$ 为当前 $x^{(t)}$下内点和离群点聚类间的距离，并用${\delta }^{(0)}$归一化（line 8）。
• 归一化作用见下方 Remark 16。

---

终止条件

ADAPT-MinT 在以下情况下终止：

1. 达到最大迭代次数（line 4 中的“for”循环）；
2. ${\delta }^{(t)}$收敛到稳定值，表示内点和离群点聚类已收敛。

具体来说，当连续MinSamples