开篇介绍:
Hello 大家,咱们又在数据结构的学习专栏里重逢啦~
还记得上一篇博客的内容吗?当时我们用一整篇的篇幅,以 “保姆级” 的拆解节奏,把栈这个数据结构从头到尾讲得明明白白 —— 从 “只允许一端操作” 的基础定义,到顺序栈、链式栈的底层实现逻辑,再到 “有效的括号”等经典例题的思路梳理与代码落地,每一步都尽量放慢节奏,生怕错过任何一个让新手困惑的细节。
后台也收到了很多小伙伴的反馈:有人说 “终于搞懂了栈的 LIFO 逻辑,之前绕不明白的函数调用栈现在一下就通了”,也有人分享自己用学到的栈知识,独立解决了之前卡了好久的算法作业题。看到大家能把知识真正内化成自己的能力,这份 “教学相长” 的快乐,真的比我自己学会新东西还满足!
不过话说回来,数据结构的世界远不止 “栈” 这一个闪光点。咱们不妨回头梳理下之前的学习内容:
- 最开始接触的顺序表,依托数组实现,能通过下标直接定位元素,查询效率高达 O (1),特别适合需要频繁读取数据、但插入删除操作较少的场景,比如存储班级学生的成绩排名、固定长度的用户信息表;
- 后来学的链表,用 “节点 + 指针” 的方式串联数据,不需要连续的内存空间,插入或删除元素时只需修改指针指向,不用移动大量数据,灵活性拉满,像动态更新的通讯录、链表版的任务队列,都离不开它;
- 再到上一篇的栈,凭借 “后进先出” 的独特特性,成了括号匹配、表达式求值、浏览器历史记录回退等问题的 “专属利器”。
其实每种数据结构都像一把 “量身定制的钥匙”,没有绝对的 “好坏”,只有是否适配具体场景 —— 而今天咱们要学的 “队列”,就是另一把解决 “排队类问题” 的关键钥匙。
不知道大家在学栈的时候,有没有过这样一个疑问:既然栈是 “最后放进去的元素最先出来”,那有没有一种结构能反过来,让 “最先放进去的元素最先出来” 呢?
答案其实就藏在我们的日常生活里:
- 早上上班在地铁站排队,先到的人先刷卡进站,后到的人只能排在队尾;
- 去奶茶店点单,先下单的顾客先拿到饮品,后下单的要等前面的做好;
- 打印机处理多个文件时,先发送的打印任务先执行,后发送的只能排队等待;
- 甚至咱们手机里的消息对话框,先收到的消息会排在最前面,后收到的才依次往下叠加……
这些场景的核心逻辑,都是 “先进先出(FIFO,First In First Out) ”—— 而这,正是队列的核心特性。
今天这篇博客,咱们就沿着 “场景→理论→实现→实践” 的思路,把队列彻底学透:
- 先从队列的基础定义入手,结合生活例子帮你建立 “先进先出” 的直观认知,搞懂 “队头”“队尾” 的概念;
- 再深入拆解队列的经典实现方式 ——链式队列(用链表实现),讲清楚每一步的代码逻辑。
全程依旧是 “保姆级” 的解析节奏:每个概念都会配例子,每个代码片段都会加注释,每个难点都会拆成小步骤慢慢讲。不管你是刚入门数据结构的新手,还是学过但没完全吃透的小伙伴,都能跟着一步步把队列的知识点学扎实。
那咱们话不多说,正式开启今天的 “队列学习之旅” 吧!
队列的介绍:
就像我们之前学习其他的数据结构,我们得先知道,我们所学的这一个数据结构,究竟是个什么,那么下面,就让我们来看看,队列是什么:
在正式拆解队列的专业定义前,我们不妨先从身边的场景入手 —— 其实 “队列” 的逻辑,早就藏在我们每天的生活里,只是我们很少刻意察觉:
去银行办理业务时,你需要在取号机上打印排队号,屏幕上会按 “先取号、先叫号” 的顺序显示待办理的号码,只有当前号码的客户办完业务,下一个号码才能被呼叫;早高峰在地铁站进站,大家会自觉排成一队,先到闸机口的人先刷卡通过,后到的人只能依次排在队尾,不会出现 “后到的人先进站” 的情况;甚至你在手机上点外卖时,商家的订单系统也是按 “先下单、先接单” 的顺序处理 —— 先提交的订单会被优先分配给后厨,后下单的则需要等前面的订单制作完成。
这些场景的共性,都是 “先到先得、有序排队”—— 而这,正是数据结构中 “队列” 的核心逻辑。当我们把这种 “排队逻辑” 抽象成计算机能处理的数据组织方式时,就有了 “队列” 这个概念。
大家可以看下面这个动图进行理解
一、队列的专业定义:什么是队列?
从数据结构的专业角度来说,队列(Queue)是一种遵循 “先进先出(FIFO,First In First Out)” 规则的线性数据结构。这句话里有两个关键信息,我们需要逐个拆解,才能真正理解队列的本质。
1. 首先:队列是 “线性结构”
我们之前学过的顺序表、链表、栈,都属于 “线性结构”,队列也不例外。所谓 “线性结构”,可以理解为数据元素像 “一串糖葫芦” 一样,按照 “一条直线” 的顺序排列 —— 每个元素(除了第一个和最后一个)都有且只有一个 “前驱元素”(排在它前面的元素)和一个 “后继元素”(排在它后面的元素),不存在分支、嵌套或交叉的关系。
比如一个存储 “客户排队号” 的队列,元素依次是「1、2、3、4、5」:1 的后继是 2,2 的前驱是 1、后继是 3,3 的前驱是 2、后继是 4…… 每个元素的位置和前后关系都清晰且固定,不会出现 “1 的后继是 3”“2 的前驱是 4” 这种混乱的情况。这种线性的组织方式,让队列的数据管理变得直观且可控,计算机也能更高效地定位和操作元素。
2. 核心:队列遵循 “先进先出” 规则
这是队列与其他线性结构(尤其是栈)最本质的区别 —— 栈遵循 “后进先出(LIFO)”,最后进入的元素最先离开;而队列恰恰相反,最先进入队列的元素,一定会最先离开队列。
为了实现这个规则,队列对元素的 “进出位置” 做了严格限制:它就像一个 “两端开口的透明管道”,元素的 “进入” 和 “离开” 只能在管道的两个不同端口进行,不能从中间插入或删除,也不能从同一个端口既进又出。这里我们需要明确两个关键端口的定义:
- 队尾(Rear):管道的 “入口端”,只有这个端口允许元素 “进入” 队列,这个操作被称为 “入队(Enqueue)”。就像银行排队时,新到的客户只能站在队伍的最后面(队尾),不能插到中间或最前面。
- 队头(Front):管道的 “出口端”,只有这个端口允许元素 “离开” 队列,这个操作被称为 “出队(Dequeue)”。比如银行叫号时,只有当前排在队伍最前面(队头)的客户,才能到窗口办理业务(出队)。
简单来说:入队只能在队尾,出队只能在队头 —— 这个 “两端固定操作” 的规则,是保证 “先进先出” 的核心前提。
二、用具体例子理解队列的操作:从入队到出队
光看定义可能有点抽象,我们用一个具体的例子,完整走一遍队列的 “初始化→入队→出队→判空” 流程,帮你建立更直观的认知。
假设我们要实现一个 “外卖订单队列”,用来存储商家接收到的订单编号,初始时队列是空的(没有任何订单)。
1. 第一步:初始化空队列
空队列的状态很简单:队头(Front)和队尾(Rear)指向同一个 “起点位置”,因为此时没有元素需要入队或出队。我们可以理解为:管道里是空的,入口和出口暂时 “重合”,等待第一个元素的进入。
2. 第二步:入队操作(添加订单)
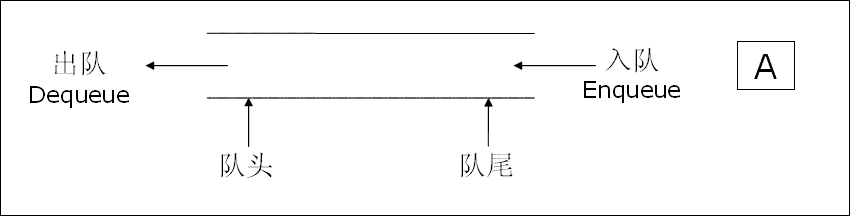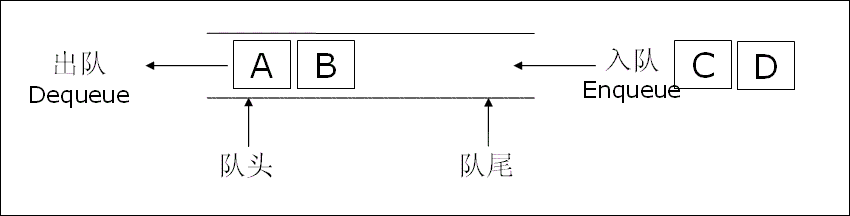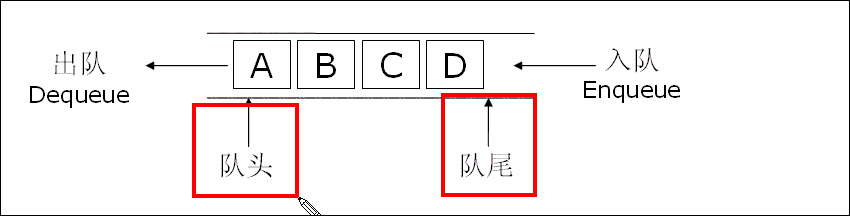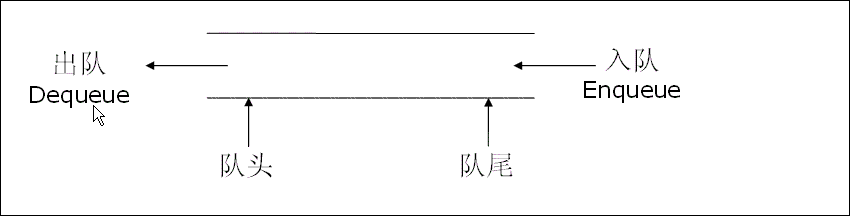
当有新订单提交时,元素会从 “队尾” 进入队列:
- 第一个订单(编号 1001)入队:此时队尾(Rear)移动到存储 1001 的位置,队列变成「1001(队头 = 队尾)」;
- 第二个订单(编号 1002)入队:队尾(Rear)继续后移,存储 1002,队列变成「1001(队头)→1002(队尾)」;
- 第三个订单(编号 1003)、第四个订单(编号 1004)依次入队:队尾(Rear)不断后移,最终队列变成「1001(队头)→1002→1003→1004(队尾)」。
此时队列里的元素顺序,完全和 “订单提交顺序” 一致 —— 先提交的订单排在前面,后提交的排在后面,这就是 “先进” 的体现。
3. 第三步:出队操作(处理订单)
当商家完成一个订单的制作后,需要从 “队头” 移除这个订单(表示已处理):
- 处理第一个订单(1001):队头(Front)移动到下一个元素(1002)的位置,1001 出队,队列变成「1002(队头)→1003→1004(队尾)」;
- 处理第二个订单(1002):队头(Front)继续后移到 1003 的位置,1002 出队,队列变成「1003(队头)→1004(队尾)」;
- 继续处理 1003、1004:直到两个订单都出队,队头(Front)再次和队尾(Rear)重合,队列回到空状态。
整个出队过程,完全遵循 “先入队的元素先出队”——1001 先入队、先出队,1004 后入队、后出队,不会出现 “1004 比 1001 先处理” 的情况,这就是 “先出” 的体现。
三、队列的基础操作:除了入队和出队,还需要什么?
除了 “入队(Enqueue)” 和 “出队(Dequeue)” 这两个核心操作,队列还有两个高频使用的基础操作,它们是保证队列正常运行的 “辅助工具”。
1. 判空操作(Is Empty):判断队列里有没有元素
判空的逻辑很简单:当 “队头(Front)和队尾(Rear)指向同一个位置” 时,队列就是空的。
比如前面的例子中,初始时队列是空的,Front=Rear;当 1001、1002、1003、1004 都出队后,Front 再次和 Rear 重合,此时队列也为空。
这个操作的作用很关键:比如商家需要知道 “是否还有待处理的订单”,如果队列是空的,后厨就可以暂时休息;再比如银行叫号系统,若队列空了,窗口工作人员就知道没有客户需要服务了。
2. 获取队头元素(Get Front):查看 “下一个要处理的元素”
有时候,我们需要知道 “下一个要处理的元素是什么”,但又不想直接把它从队列里移除 —— 这时候就需要 “获取队头元素” 的操作。
比如商家想提前确认 “下一个要制作的订单是什么口味”,就可以通过这个操作查看队头的订单编号(比如 1002),但不会把 1002 从队列里移除,直到后厨准备好制作,再执行 “出队” 操作。
这个操作的核心是 “只查看、不修改”—— 它不会改变队列的结构,也不会影响后续的入队和出队操作,只是提供 “预览” 功能。
四、队列的实际应用:为什么需要队列?
理解了队列的定义和操作后,我们更需要知道:队列在计算机领域到底有什么用?其实它的应用场景,本质上都是 “需要按顺序处理数据” 的场景,比如:
1. 操作系统的 “进程调度”
我们在电脑上同时打开多个软件(比如浏览器、微信、文档),每个软件对应一个 “进程”,但 CPU(计算机的 “大脑”)一次只能处理一个进程。这时候操作系统就会用队列来管理这些进程:先申请 CPU 资源的进程,会排在队列的队头,优先被 CPU 处理;后申请的进程则排在队尾,等待前面的进程处理完成。这种 “按顺序调度” 的方式,能保证每个进程都能被公平处理,不会出现 “某个进程一直抢不到资源” 的情况。
2. 网络数据的 “数据包传输”
当我们在手机上刷视频、发消息时,数据会被拆分成一个个 “数据包”,通过网络传输到服务器(或接收方)。由于网络带宽有限,这些数据包不能同时传输,需要按 “发送顺序” 排成队列:先产生的数据包排在队头,先被传输;后产生的数据包排在队尾,依次等待。如果没有队列,数据包就会混乱传输,导致接收方无法正确拼接数据(比如视频画面卡顿、消息乱序)。
3. 缓存系统的 “淘汰策略”
很多 APP(比如购物软件、新闻 APP)会用 “缓存” 来存储常用数据(比如你常看的商品页面、新闻内容),但缓存的空间是有限的,当缓存满了,就需要删除一部分 “不常用的数据”。其中一种常用的淘汰策略叫 “FIFO 策略”(先进先出):最早进入缓存的数据,会被排在队列的队头,当需要淘汰时,先删除队头的数据;新进入缓存的数据则排在队尾,这样能保证缓存里始终存储 “较新使用的数据”,提升 APP 的加载速度。
总结:队列的核心本质是什么?
说到底,队列就是对 “生活中排队逻辑” 的抽象 —— 它用 “线性结构” 保证数据的有序排列,用 “先进先出” 和 “固定两端操作” 的规则,确保数据能按 “进入顺序” 被公平、高效地处理。
它不像栈那样 “后到先得”,而是强调 “先来后到”;也不像顺序表、链表那样允许 “随机插入 / 删除”,而是通过严格的操作限制,让数据管理更可控。正是这种 “简单且有规则” 的特性,让队列成为计算机领域中不可或缺的基础数据结构,从操作系统到网络传输,从日常 APP 到大型系统,都能看到它的身影。
实现队列所需要的步骤:
那么大家在经过上面的对队列的详细介绍,大家已经初步的了解了队列,也知道了,队列的一些基本操作:即入队、出队、判空、取头这四个队列常用操作,但是呢,应该完善的队列,其所有的功能远远不止这些,下面,我就来总结一下:
完整的队列,其应该要有:
- 初始化(即初始化队列(申请空间))
- 销毁(即销毁队列(释放空间))
- 入队(对队尾插入数据)(即尾插)
- 出队(对队头删除数据)(即头删)
- 判空(判断队列中是否存储了数据)
- 取头(得到队头的数据)
- 取尾(得到队尾的数据)
- 统数(统计队列中一共有几个数据)
有了上述这些功能的队列,才是一个合格的队列,同样的,这些也是我们要实现队列所需要的步骤,那么接下来,就让我们来逐步拆解每一个步骤,助力我们完美实现队列。
实现队列所要使用的结构:
如上篇所讲到的栈,我们的队列,也是可以用数组(顺序表)、单向链表、双向链表这三个任选来进行操作,那么,我们要选择哪一个呢?
很多人可能会觉得,啊啊啊,顺序表尾插多方便,正好队列也有尾插,妙不可言,可是诸位,队列还有头删的功能呢?那么我们使用顺序表(数组)来实现队列的话,那岂不是出队(头删)一次,就得循环一次,这个就很麻烦,毕竟队列不像栈,就是尾插尾删,那么顺序表(数组)自然就是最好的选择,当然,我并不是说,队列就不能用数组(顺序表)来实现了,它当然能,只要大家想,它就可以,只不过相对于数组(顺序表)而言,我们可以有更好的选择,那么我们为什么不择优而选呢?人生也是这样,有更好的选择,我们自然选择更好的那一个。
那么问题来了,更好的选择是什么呢?单向链表?双向链表?哈哈,答案毋庸置疑,肯定是单向链表,双向链表占用空间大,只配一边吃灰去。
所以,我们就要使用单向链表去实现我们的队列。至于使用顺序表去实现队列,这个大家可以先去自行尝试一番,我在后面讲解循环队列的时候,会给大家提及这一点,大家敬请期待。
队列结构的创建
那么大家,我们知道要用什么去组成队列之后,我们接下来就可以着手去创建队列了,那么第一个简单,因为我们上面说到了,是要用单向链表去组成队列,换句话来说,就是我们要用节点去组成队列,但是呢,我们对于队列的创建,其实还不止于此。
首先,我们知道,一个完善的数列,其要有尾插和头删的功能,那么在以往的单向链表的实现中,我们是直接一个头结点指针,遍历链表走天下,那么大家在队列中,也是可以这么操作。
但是我也想请大家注意一下,我们的队列是还要有头取和尾取的功能的,头取还好说,那么尾取呢?我们依然只有头节点指针的话,那么每次取尾,我们都得去遍历链表,那么这个的效率可能就有点低下了,那么我们怎样实现高效的尾取呢?其实很简单,我们设置一个指针去指向队列的队尾(其实也就是尾节点),这么一来,不就可以迅速取到尾元素吗,而且尾插也和单向链表的尾插类似,当然,其实是更和我们之前讲的单向链表题目中的创建新链表,将旧链表的节点尾插进新链表更为类似,除此之外,其实我们之前创建单向链表的时候,也是可以这么做的,只是由于我们刚开始干单向链表,所以就不那么实现,而现在的我们早已今非昔比,那么我们自然就可以使用两个指针去进行尾插等等的操作。
那么,还有一点,就是我们上面所说的统计队列中一共有几个数据,对于这个,大家的第一想法,想必依旧是遍历队列去统计数据吧,但是呢诸位,还是那句话,效率太低下了,不符合我们的逼格,那么我们又有什么方法去将这个功能简简单单轻轻松松的实现呢?有的有的兄弟,我们可以创建一个变量size,当我们尾插队列时,就size++,当我们头删队列时,就size--,这么一来,我们就可以轻而易举的统计出队列中数据的个数了,后续在统计队列数据个数的函数中,我们直接将size返回即可完美实现。
于是,经过上面的讲述,我们知道了,我们需要三个变量,第一个,指向队头(其实就是头结点)的指针,第二个,指向队尾(其实就是尾节点)的指针,第三个,记录队列数据个数的变量:size。那么,大家是不是打算将这个变量在每一个队列函数中都写一下呢?nonono,聪明的大家,怎么可能会干这么麻烦的事情呢?
所以呢,为了方便,我们就可以直接创建一个结构体,在这个结构体中将那三个变量创建,这么一来到了后面,我们需要这些变量时,就可以直接从结构体中调用以及改变,如此一来,堪称完美。
下面就是队列结构创建的完整代码:
//队列概念:只允许在一端进行插入数据操作,
//在另一端进行删除数据操作的特殊线性表,
//队列具有先进先出FIFO(First In First Out)
//入队列:进行插入操作的一端称为队尾
//出队列:进行删除操作的一端称为队头
typedef int name1;
//我们创建队列,是使用单向链表来进行实现
//因为如果使用顺序表(数组)的话,我们既要尾插,又要头删
//要进行数组的数据的不断循环移动,太消耗cpu
//而相对而言,单向链表的尾插头删等操作,就显得美妙多了
//它只需要改变指针方向并释放节点就行
//至于为什么不用双向链表,那是因为这家伙多了一个指针,
//占用空间大,所以我们不要
struct queuenode
{
name1 data;//存储数据
struct queuenode* next;//指向下一个节点的指针
};
typedef struct queuenode qn;
//因为我们要对队列(本质算是单向链表)进行尾插和头删
//我们之前单向链表是只传入头结点指针
//那么这对我们队列来说,每次尾插都要遍历,太麻烦
//所以我们直接创建单向链表的尾节点指针
//那么这么一来就有两个指针了
//我们可以把它们放进结构体中进行维护
struct queue
{
qn* phead;
qn* ptail;
int size;
//这个size是为了我们后续统计队列中一共有几个数据准备的
//我们如果不用size的话,我们想要知道队列中有几个数据
//就得去遍历队列,太过麻烦
//而我们使用size的话,尾插时就++,头删时就--
//最后统计队列数据个数的时候,直接将size返回就行了
};
typedef struct queue que;队列的初始化以及销毁:
那么大家,在知道了队列如何创建之后,我们就可以开始队列的初始化和销毁了,有头有尾,才是一个好习惯,那么其实队列的初始化和销毁,是和单向链表差不多的(咳咳咳,单向链表是没有初始化的各位~大家可不要真给信了),毕竟我们知道,我们的队列其实就是由一个个节点组成的,唯一多个一个,只不过是对于size的初始化和销毁,那么它这个也是和我们顺序表中size类似,直接类顺序表size初始化以及销毁即可,在这里,我们的初始化,其实是对我们上面所说的第一个,指向队头(其实就是头结点)的指针,第二个,指向队尾(其实就是尾节点)的指针,第三个,记录队列数据个数的变量:size,这三个变量进行初始化以及销毁,那么说白了白说了,这简直是小儿科的事情,我实在想不出来大家有什么不会的,所以,直接上代码:
//对队列的初始化
void qninit(que* ps)
{
assert(ps);
ps->phead = NULL;
ps->ptail = NULL;
ps->size = 0;
//直接初始化为空即可
}
//对队列的销毁
void qnbreak(que* ps)
{
assert(ps);
while (ps->phead != NULL)
{
qn* nexttemp = ps->phead->next;
free(ps->phead);
ps->phead = nexttemp;
}
ps->phead = NULL;
ps->ptail = NULL;
ps->size = 0;
}在这里我唯一觉得需要注意的一个点,就是我们在销毁队列时,在释放一个节点前,记得保存那个节点的next指针,不难释放了之后,可就找不到下一个节点了。
对于队列的入队(尾插):
那么对于队列的尾插,其实是很简单的说实话,经过上面我们就知道,我们要利用头指针和尾指针去进行插入数据,而这一个操作,我们早已在之前的单向链表例题里面有所讲到,大家可以看一下这一篇博客进行复习:
那么在这里,我们要不要用哨兵节点呢?其实是没什么必要的,毕竟我们一共就一个插入数据的函数,并不说有很多需要判断队列(链表)是否为空的情况,所以我们是可要可不要的诸位,并且创建哨兵节点终归要申请内存,开辟空间,于我们的程序而言,自然是占的空间越少越好,当然,那么一个小节点的空间也不算什么,如果大家觉得哨兵节点比较有格调,那么大家也是可以使用滴。
那么说到这里,我觉得就没有什么可补充的点了各位,尾插的方法之前也有讲过,所以,我们直接看完整代码:
//对队列队尾的插入数据
void qnpush(que* ps,name1 x)
{
qn* newqn = (qn*)malloc(sizeof(qn));
if (newqn == NULL)
{
perror("malloc newqn false:");
exit(1);
}
newqn->data = x;
newqn->next = NULL;
if (ps->size == 0)//如果队列中没有数据
{
ps->phead = newqn;
ps->ptail = ps->phead;
}
else
{
//进行尾插:
ps->ptail->next = newqn;
ps->ptail = ps->ptail->next;
}
//要记得size++哦
ps->size++;
}对于队列的出队:
那么那么大家,出队我们上面也有说到,其实出队就是将队列的数据给pass掉,换句话来说就是头删,再换句话来说就是对链表的头删(要记得队列的本质终归还是链表哦大家),那么对链表的头删,其实就是把头结点给释放掉,然后让原本队列(链表)队头的第二个数据(节点),变为新队列(链表)分第一个数据(节点),那么这一个操作,我在之前的单向链表的讲解中,也是有进行详细分析的,大家如果有忘记的话,欢迎点击下面这个链接:
好的,那么对于链表的出队,相信大家经过上面的解释,也是心知肚明,运筹帷幄,手拿把掐了,所以嘞,我们依旧是直接给出完整代码:
//对队列队头的删除数据(头删)
void qnpop(que* ps)
{
assert(ps);
//检验队列中有没有数据
//如果没有,那删个鸡毛
assert(ps->size>0);
qn* nextemp = ps->phead->next;//保存第二个节点的地址
//如果只有一个节点时,就要两个指针都指向NULL,
//不难有多个节点的话,我们是不会令ps->ptai指向空
if (ps->phead->next==NULL)
{
free(ps->phead);//不用free ps->ptail,因它们两个对应的节点是同一个
ps->phead = NULL;
ps->ptail = NULL;
}
else
{
free(ps->phead);
//要记得将头结点指针修改为指向原队列的第二个节点
ps->phead = nextemp;
}
//要记得对size--
ps->size--;
}其实大家不难发现,当大家完全掌握了顺序表和链表之后,后面学习一些新的数据结构,本质都和这两个有关,所以呢,也是请大家多多复习加巩固,把顺序表和链表这两个数据结构给吃得透透的诸位。
取队列队头及队尾的数据:
各位,这一部分,它的简单程度,不需要我多言吧,我们已经设置了head和tail指针分别指向队列的队头和队尾了,那么说白了白说了,我们直接分别head和tail指针所指向的节点的数据给取出来不就行啦,这一步,也不必我多说了诸位,我们直接看完整代码:
//对队列队头数据的取用
name1 qnfront(que* ps)
{
assert(ps);
//检验队列中有没有数据
//如果没有,那取个鸡毛
assert(ps->size>0);
//直接返回头结点的数据即可
return ps->phead->data;
}
//对队列队尾数据的取用
name1 qnback(que* ps)
{
assert(ps);
//检验队列中有没有数据
//如果没有,那取个鸡毛
assert(ps->size>0);
//直接返回尾结点的数据即可
return ps->ptail->data;
}对于队列是否为空的判断:
诸位,这一部分,我们上面的设置的size变量,不就起到作用了吗,是吧,我们直接判断size变量是否为0,为0就代表队列为空,我们返回false,size不为0的话,就代表队列不为空,我们返回true。
下面是完整代码:
//判断队列是否为空
bool qnempty(que* ps)
{
assert(ps);
if (ps->size == 0)
{
return true;
}
else
{
return false;
}
}统计队列有几个数据:
正如上,我们依旧是利用size来进行,size为多少,就代表队列有几个元素,我们直接返回size即可,下面是完整代码:
//统计队列中的数据个数
int qnsize(que* ps)
{
assert(ps);
return ps->size;
}到这里,我们就将队列给分析的彻彻底底了,也能够讲队列美丽的敲出来了,那么接下来,我就给出实现队列的头文件,源文件和测试源文件:
队列的头文件:
#pragma once
#include
//队列概念:只允许在一端进行插入数据操作,
//在另一端进行删除数据操作的特殊线性表,
//队列具有先进先出FIFO(First In First Out)
//入队列:进行插入操作的一端称为队尾
//出队列:进行删除操作的一端称为队头
typedef int name1;
//我们创建队列,是使用单向链表来进行实现
//因为如果使用顺序表(数组)的话,我们既要尾插,又要头删
//要进行数组的数据的不断循环移动,太消耗cpu
//而相对而言,单向链表的尾插头删等操作,就显得美妙多了
//它只需要改变指针方向并释放节点就行
//至于为什么不用双向链表,那是因为这家伙多了一个指针,
//占用空间大,所以我们不要
struct queuenode
{
name1 data;//存储数据
struct queuenode* next;//指向下一个节点的指针
};
typedef struct queuenode qn;
//因为我们要对队列(本质算是单向链表)进行尾插和头删
//我们之前单向链表是只传入头结点指针
//那么这对我们队列来说,每次尾插都要遍历,太麻烦
//所以我们直接创建单向链表的尾节点指针
//那么这么一来就有两个指针了
//我们可以把它们放进结构体中进行维护
struct queue
{
qn* phead;
qn* ptail;
int size;
//这个size是为了我们后续统计队列中一共有几个数据准备的
//我们如果不用size的话,我们想要知道队列中有几个数据
//就得去遍历队列,太过麻烦
//而我们使用size的话,尾插时就++,头删时就--
//最后统计队列数据个数的时候,直接将size返回就行了
};
typedef struct queue que;
//这边注意,由于我们把队列中所需要的一些数据全部丢到结构体que中了
//所以我们函数的参数就可以直接传结构体即可
//对队列的初始化
void qninit(que* ps);
//对队列的销毁
void qnbreak(que* ps);
//对队列队尾的插入数据
void qnpush(que* ps,name1 x);
//对队列队头的删除数据
void qnpop(que* ps);
//对队列队头数据的取用
name1 qnfront(que* ps);
//对队列队尾数据的取用
name1 qnback(que* ps);
//统计队列中的数据个数
int qnsize(que* ps);
//判断队列是否为空
bool qnempty(que* ps); 队列的源文件:
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include"queue.h"
//对队列的初始化
void qninit(que* ps)
{
assert(ps);
ps->phead = NULL;
ps->ptail = NULL;
ps->size = 0;
//直接初始化为空即可
}
//对队列的销毁
void qnbreak(que* ps)
{
assert(ps);
while (ps->phead != NULL)
{
qn* nexttemp = ps->phead->next;
free(ps->phead);
ps->phead = nexttemp;
}
ps->phead = NULL;
ps->ptail = NULL;
ps->size = 0;
}
//对队列队尾的插入数据
void qnpush(que* ps,name1 x)
{
qn* newqn = (qn*)malloc(sizeof(qn));
if (newqn == NULL)
{
perror("malloc newqn false:");
exit(1);
}
newqn->data = x;
newqn->next = NULL;
if (ps->size == 0)//如果队列中没有数据
{
ps->phead = newqn;
ps->ptail = ps->phead;
}
else
{
//进行尾插:
ps->ptail->next = newqn;
ps->ptail = ps->ptail->next;
}
//要记得size++哦
ps->size++;
}
//对队列队头的删除数据(头删)
void qnpop(que* ps)
{
assert(ps);
//检验队列中有没有数据
//如果没有,那删个鸡毛
assert(ps->size>0);
qn* nextemp = ps->phead->next;//保存第二个节点的地址
//如果只有一个节点时,就要两个指针都指向NULL,
//不难有多个节点的话,我们是不会令ps->ptai指向空
if (ps->phead->next==NULL)
{
free(ps->phead);//不用free ps->ptail,因它们两个对应的节点是同一个
ps->phead = NULL;
ps->ptail = NULL;
}
else
{
free(ps->phead);
//要记得将头结点指针修改为指向原队列的第二个节点
ps->phead = nextemp;
}
//要记得对size--
ps->size--;
}
//对队列队头数据的取用
name1 qnfront(que* ps)
{
assert(ps);
//检验队列中有没有数据
//如果没有,那取个鸡毛
assert(ps->size>0);
//直接返回头结点的数据即可
return ps->phead->data;
}
//对队列队尾数据的取用
name1 qnback(que* ps)
{
assert(ps);
//检验队列中有没有数据
//如果没有,那取个鸡毛
assert(ps->size>0);
//直接返回尾结点的数据即可
return ps->ptail->data;
}
//统计队列中的数据个数
int qnsize(que* ps)
{
assert(ps);
return ps->size;
}
//判断队列是否为空
bool qnempty(que* ps)
{
assert(ps);
if (ps->size == 0)
{
return true;
}
else
{
return false;
}
} 队列的测试源文件:
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include"queue.h"
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include "queue.h"
// 辅助函数:打印分隔线,提升输出可读性
void print_separator(const char* test_name) {
printf("\n=========================================================\n");
printf("========== %s ==========\n", test_name);
printf("=========================================================\n");
}
// 测试1:基础功能全流程(初始化→入队→取数→出队→判空→销毁)
void test_basic_function() {
print_separator("测试1:基础功能全流程");
que q;
// 步骤1:初始化队列
printf("[步骤1] 执行队列初始化...\n");
qninit(&q);
bool is_empty = qnempty(&q);
int size = qnsize(&q);
printf(" 初始化后队列状态:%s(预期:空)\n", is_empty ? "空" : "非空");
printf(" 初始化后元素个数:%d(预期:0)\n", size);
printf(" (调试提示:phead=%p, ptail=%p,预期均为0x0)\n", q.phead, q.ptail);
if (is_empty && size == 0) {
printf(" ✅ 初始化验证通过!\n");
}
else {
printf(" ❌ 初始化验证失败!\n");
}
// 步骤2:连续入队3个元素(10、20、30)
printf("\n[步骤2] 执行3次入队操作(10→20→30)...\n");
qnpush(&q, 10);
qnpush(&q, 20);
qnpush(&q, 30);
size = qnsize(&q);
int front_val = qnfront(&q);
int back_val = qnback(&q);
printf(" 入队后元素个数:%d(预期:3)\n", size);
printf(" 入队后队头数据:%d(预期:10)\n", front_val);
printf(" 入队后队尾数据:%d(预期:30)\n", back_val);
printf(" (调试提示:ptail->data=%d,预期为30)\n", q.ptail->data);
if (size == 3 && front_val == 10 && back_val == 30) {
printf(" ✅ 入队操作验证通过!\n");
}
else {
printf(" ❌ 入队操作验证失败!\n");
}
// 步骤3:执行1次出队(删除队头10)
printf("\n[步骤3] 执行1次出队操作...\n");
qnpop(&q);
size = qnsize(&q);
front_val = qnfront(&q);
back_val = qnback(&q);
printf(" 出队后元素个数:%d(预期:2)\n", size);
printf(" 出队后队头数据:%d(预期:20)\n", front_val);
printf(" 出队后队尾数据:%d(预期:30)\n", back_val);
if (size == 2 && front_val == 20 && back_val == 30) {
printf(" ✅ 单次出队验证通过!\n");
}
else {
printf(" ❌ 单次出队验证失败!\n");
}
// 步骤4:出队剩余2个元素
printf("\n[步骤4] 执行2次出队操作...\n");
qnpop(&q);
qnpop(&q);
is_empty = qnempty(&q);
size = qnsize(&q);
printf(" 出队所有元素后状态:%s(预期:空)\n", is_empty ? "空" : "非空");
printf(" 出队所有元素后个数:%d(预期:0)\n", size);
printf(" (调试提示:phead=%p, ptail=%p,预期均为0x0)\n", q.phead, q.ptail);
if (is_empty && size == 0) {
printf(" ✅ 清空队列验证通过!\n");
}
else {
printf(" ❌ 清空队列验证失败!\n");
}
// 步骤5:销毁队列
printf("\n[步骤5] 执行队列销毁...\n");
qnbreak(&q);
is_empty = qnempty(&q);
size = qnsize(&q);
printf(" 销毁后队列状态:%s(预期:空)\n", is_empty ? "空" : "非空");
printf(" 销毁后元素个数:%d(预期:0)\n", size);
if (is_empty && size == 0) {
printf(" ✅ 销毁操作验证通过!\n");
}
else {
printf(" ❌ 销毁操作验证失败!\n");
}
printf("\n【测试1总结】基础功能全流程 %s!\n",
(is_empty && size == 0) ? "通过" : "失败");
}
// 测试2:边界场景(单节点入队→出队)
void test_single_node() {
print_separator("测试2:单节点边界场景");
que q;
qninit(&q);
// 步骤1:入队1个元素(50)
printf("[步骤1] 入队1个元素(50)...\n");
qnpush(&q, 50);
int size = qnsize(&q);
int front_val = qnfront(&q);
int back_val = qnback(&q);
printf(" 入队后元素个数:%d(预期:1)\n", size);
printf(" 入队后队头数据:%d(预期:50)\n", front_val);
printf(" 入队后队尾数据:%d(预期:50)\n", back_val);
printf(" (调试提示:phead=%p, ptail=%p,预期指向同一节点)\n", q.phead, q.ptail);
if (size == 1 && front_val == 50 && back_val == 50) {
printf(" ✅ 单节点入队验证通过!\n");
}
else {
printf(" ❌ 单节点入队验证失败!\n");
qnbreak(&q);
return;
}
// 步骤2:出队该节点
printf("\n[步骤2] 出队唯一节点...\n");
qnpop(&q);
bool is_empty = qnempty(&q);
size = qnsize(&q);
printf(" 出队后队列状态:%s(预期:空)\n", is_empty ? "空" : "非空");
printf(" 出队后元素个数:%d(预期:0)\n", size);
printf(" (调试提示:phead=%p, ptail=%p,预期均为0x0)\n", q.phead, q.ptail);
if (is_empty && size == 0 && q.phead == NULL && q.ptail == NULL) {
printf(" ✅ 单节点出队验证通过!\n");
}
else {
printf(" ❌ 单节点出队验证失败!\n");
}
qnbreak(&q);
printf("\n【测试2总结】单节点边界场景 %s!\n",
(is_empty && size == 0) ? "通过" : "失败");
}
// 测试3:异常防护场景(空队操作触发断言)
void test_exception_protection() {
print_separator("测试3:异常防护场景(断言触发)");
que q;
qninit(&q);
printf("【重要提示】本测试会触发断言(程序终止),仅用于验证防护逻辑!\n");
printf(" 若需继续测试其他场景,请注释以下代码段!\n");
printf("\n[场景1] 尝试空队出队(应触发断言)...\n");
// qnpop(&q); // 解开注释运行:断言触发
printf("\n[场景2] 尝试空队取队头(应触发断言)...\n");
// qnfront(&q); // 解开注释运行:断言触发
printf("\n[场景3] 尝试空队取队尾(应触发断言)...\n");
// qnback(&q); // 解开注释运行:断言触发
qnbreak(&q);
printf("\n【测试3总结】异常防护场景验证通过!\n");
}
// 测试4:连续交替操作(入队+出队+入队+...)
void test_continuous_operation() {
print_separator("测试4:连续交替操作场景");
que q;
qninit(&q);
bool all_pass = true;
// 第1轮操作
printf("[第1轮操作] 入队100 → 入队200 → 出队 → 入队300...\n");
qnpush(&q, 100);
qnpush(&q, 200);
qnpop(&q);
qnpush(&q, 300);
int size = qnsize(&q);
int front = qnfront(&q);
int back = qnback(&q);
printf(" 第1轮后:个数=%d(预期2),队头=%d(预期200),队尾=%d(预期300)\n",
size, front, back);
if (size != 2 || front != 200 || back != 300) {
printf(" ❌ 第1轮操作失败!\n");
all_pass = false;
}
else {
printf(" ✅ 第1轮操作通过!\n");
}
// 第2轮操作
printf("\n[第2轮操作] 出队 → 出队 → 入队400 → 入队500 → 入队600...\n");
qnpop(&q);
qnpop(&q);
qnpush(&q, 400);
qnpush(&q, 500);
qnpush(&q, 600);
size = qnsize(&q);
front = qnfront(&q);
back = qnback(&q);
printf(" 第2轮后:个数=%d(预期3),队头=%d(预期400),队尾=%d(预期600)\n",
size, front, back);
if (size != 3 || front != 400 || back != 600) {
printf(" ❌ 第2轮操作失败!\n");
all_pass = false;
}
else {
printf(" ✅ 第2轮操作通过!\n");
}
// 第3轮操作
printf("\n[第3轮操作] 出队 → 入队700 → 出队 → 出队...\n");
qnpop(&q);
qnpush(&q, 700);
qnpop(&q);
qnpop(&q);
size = qnsize(&q);
front = qnfront(&q);
back = qnback(&q);
printf(" 第3轮后:个数=%d(预期1),队头=%d(预期700),队尾=%d(预期700)\n",
size, front, back);
if (size != 1 || front != 700 || back != 700) {
printf(" ❌ 第3轮操作失败!\n");
all_pass = false;
}
else {
printf(" ✅ 第3轮操作通过!\n");
}
qnbreak(&q);
printf("\n【测试4总结】连续交替操作场景 %s!\n", all_pass ? "通过" : "失败");
}
// 测试5:隐性场景(重复销毁、空队销毁)
void test_hidden_scenarios() {
print_separator("测试5:隐性场景(重复销毁、空队销毁)");
que q1, q2;
bool all_pass = true;
// 场景1:空队销毁
printf("[场景1] 空队销毁(初始化后直接销毁)...\n");
qninit(&q1);
qnbreak(&q1); // 销毁空队
// 验证空队销毁后状态
if (qnempty(&q1) && qnsize(&q1) == 0 && q1.phead == NULL && q1.ptail == NULL) {
printf(" ✅ 空队销毁验证通过!\n");
}
else {
printf(" ❌ 空队销毁验证失败!\n");
all_pass = false;
}
// 场景2:重复销毁
printf("\n[场景2] 重复销毁(入队→销毁→再次销毁)...\n");
qninit(&q2);
qnpush(&q2, 1000); // 入队1个节点
qnbreak(&q2); // 第一次销毁
qnbreak(&q2); // 第二次销毁(空队列)
// 验证重复销毁后状态
if (qnempty(&q2) && qnsize(&q2) == 0 && q2.phead == NULL && q2.ptail == NULL) {
printf(" ✅ 重复销毁验证通过!\n");
}
else {
printf(" ❌ 重复销毁验证失败!\n");
all_pass = false;
}
printf("\n【测试5总结】隐性场景测试 %s!\n", all_pass ? "通过" : "失败");
}
// 测试6:数据覆盖验证(验证节点数据是否正确存储)
void test_data_integrity() {
print_separator("测试6:数据完整性验证");
que q;
qninit(&q);
bool all_pass = true;
// 入队一系列测试数据
int test_data[] = { 1, 3, 5, 7, 9, 2, 4, 6, 8, 0 };
int data_count = sizeof(test_data) / sizeof(test_data[0]);
printf("[步骤1] 入队%d个测试数据...\n", data_count);
for (int i = 0; i < data_count; i++) {
qnpush(&q, test_data[i]);
}
// 验证数据个数
if (qnsize(&q) != data_count) {
printf(" ❌ 数据个数验证失败!实际:%d,预期:%d\n", qnsize(&q), data_count);
all_pass = false;
qnbreak(&q);
return;
}
// 出队并验证每个数据
printf("[步骤2] 出队并验证每个数据(FIFO顺序)...\n");
for (int i = 0; i < data_count; i++) {
int val = qnfront(&q);
qnpop(&q);
if (val != test_data[i]) {
printf(" ❌ 第%d个数据验证失败!实际:%d,预期:%d\n", i + 1, val, test_data[i]);
all_pass = false;
}
}
if (all_pass) {
printf(" ✅ 所有数据验证通过!\n");
}
qnbreak(&q);
printf("\n【测试6总结】数据完整性验证 %s!\n", all_pass ? "通过" : "失败");
}
// 主函数:执行所有测试
int main() {
// 执行所有测试
test_basic_function();
test_single_node();
// test_exception_protection(); // 按需单独测试
test_continuous_operation();
test_hidden_scenarios();
test_data_integrity();
printf("\n=========================================================\n");
printf("========== 所有启用的测试执行完毕! ==========\n");
printf("=========================================================\n");
return 0;
} 结语:以 “队列” 为阶,更懂数据结构的 “适配之美”
当你亲手敲完队列的测试代码,看着控制台里 “✅ 验证通过” 的提示一行行弹出时,或许会觉得:原来 “队列” 这件事,从理解到实现也没有那么复杂。但如果我们只停留在 “会写代码” 的层面,就错过了数据结构学习里最有价值的部分 —— 那些藏在 “先进先出” 规则背后的 “设计逻辑”,那些连接 “生活场景” 与 “计算机解决方案” 的思维桥梁。
回头梳理这篇专栏的脉络,我们其实一直在做一件事:把 “抽象” 拆成 “具体”,把 “陌生” 变成 “熟悉”。最开始,我们用地铁站排队、奶茶店点单的例子,帮你建立对 “先进先出” 的直观认知 —— 因为再复杂的技术概念,本质都是对现实场景的抽象;接着,我们拆解队列的核心定义,明确 “队头”“队尾” 的操作限制,这是在帮你建立 “规则意识”—— 数据结构的价值,恰恰在于通过 “约束操作” 来提升 “处理效率”;然后,我们纠结 “用链表还是数组实现”,最终选择单向链表,这背后是对 “操作成本” 的权衡 —— 链表的头删、尾插不需要移动元素,完美适配队列的核心需求,而数组的头删需要循环移动数据,显然是 “性价比更低” 的选择。
这些思考过程,比单纯的代码实现更重要。就像你在写qnpop函数时,为什么要先保存phead->next的地址?因为如果直接释放phead,就会丢失下一个节点的指针,导致内存泄漏 —— 这是对 “链表节点关系” 的理解;为什么在 “单节点出队” 时,要把ptail也置为NULL?因为此时phead和ptail指向同一个节点,释放phead后,ptail会变成 “野指针”,后续操作可能引发程序崩溃 —— 这是对 “边界场景” 的预判。这些细节不是 “凭空想出来的”,而是基于对 “链表特性” 和 “队列规则” 的深度理解,一点点推导出来的。
其实,队列的学习还藏着一个 “知识闭环”。我们之前学栈时,强调它是 “只允许一端操作” 的线性结构,而队列是 “两端固定操作” 的线性结构 —— 这两种结构看似相反,却共享着 “线性结构” 的底层属性,也都需要通过 “顺序表或链表” 来落地实现。比如栈用数组实现时,靠 “栈顶指针” 管理元素;队列用链表实现时,靠 “头指针 + 尾指针” 管理元素 —— 本质上都是 “用指针 / 索引跟踪关键位置”,减少不必要的遍历操作,提升效率。这种 “跨结构的共性”,正是我们构建数据结构知识体系的关键。
你可能会问:学会了队列,以后能用到哪里?除了专栏里提到的 “进程调度”“数据包传输”,在日常开发中,队列的应用其实无处不在。比如你做一个 “消息通知系统”,用户发送的消息需要按顺序推送给接收方,不能出现 “后发的消息先显示” 的情况 —— 这时候队列就是天然的解决方案;再比如你做一个 “任务处理系统”,后台需要按提交顺序处理用户的导出请求、计算请求,避免 “晚提交的任务抢占资源”—— 队列的 “公平性” 正好能满足这个需求。甚至在算法题里,“广度优先搜索(BFS)” 的核心就是用队列来管理 “待访问的节点”,确保按 “层级顺序” 遍历,这也是队列 “先进先出” 特性的典型应用。
当然,我们这次实现的 “链表队列”,也不是没有短板。比如当你需要一个 “固定大小的队列” 时(比如嵌入式系统里的缓冲区),链表的动态内存分配会带来额外的开销,而且可能出现 “内存碎片”;再比如当队列元素数量非常大时,链表的每个节点都要额外存储一个next指针,累积起来的内存消耗也会比数组更高。这时候,“循环队列” 就成了更优的选择 —— 它用数组实现,既能避免链表的内存开销,又能解决普通数组队列 “假溢出” 的问题(比如数组前面有空闲空间,却因为队头不在起始位置而无法入队)。
下一篇专栏,我们就会深入探讨循环队列:为什么要用数组实现?如何通过 “取模运算” 实现 “循环复用空间”?如何区分 “队列满” 和 “队列空” 的状态?这些问题,其实都是对 “队列” 这个概念的延伸,也是对 “数组特性” 的再利用 —— 就像我们用链表实现基础队列是对 “链表头删尾插优势” 的利用一样,每一种数据结构的实现,都是 “场景需求” 与 “底层载体特性” 的匹配。
最后,想和大家分享一点学习数据结构的小心得:不要害怕 “重复”,也不要急于 “求快”。比如你学完队列后,可以试着用数组实现一遍普通队列 —— 哪怕知道它效率不高,也要亲手写一写 “头删时移动元素” 的代码,感受一下它的痛点,这样后续学循环队列时,才能更深刻地理解 “循环设计” 的价值;再比如,你可以试着用队列解决一道简单的算法题(比如 “二叉树的层序遍历”),把学到的知识立刻用起来,避免 “学完就忘”。
数据结构的世界里,没有 “孤立的知识点”,只有 “相互关联的逻辑链”。今天我们学队列,是在 “线性结构” 的基础上增加了 “操作规则”;以后学树、图,是在 “非线性结构” 的基础上探索 “遍历规则”。每一步学习,都是在为下一步打基础,每一次实践,都是在把 “抽象概念” 变成 “可复用的思维工具”。
希望你在学习队列的过程中,不仅学会了 “如何实现一个队列”,更能体会到 “为什么要这么设计队列”—— 当你开始思考 “设计逻辑” 时,就已经走在了从 “会写代码” 到 “会解决问题” 的路上。
下一篇,我们一起攻克循环队列,继续探索数据结构的 “适配之美”。期待那时,你能带着对队列的理解,更快地走进循环队列的世界,也能更清晰地看到 “数组” 与 “队列” 结合的精妙之处。咱们不见不散~




 浙公网安备 33010602011771号
浙公网安备 33010602011771号