目录
宽度优先搜索的核心思想
想象一下你在玩一个迷宫游戏,你站在起点,想知道最快到达终点的路线。BFS的策略是:
首先探索所有起点直接相连的位置(第一层)。
然后探索所有与第一层位置直接相连的、且未被访问过的位置(第二层)。
接着探索所有与第二层位置直接相连的、且未被访问过的位置(第三层)。
... 以此类推,直到找到终点或者遍历完所有能到达的点。
这种“由近及远”的搜索方式,保证了一旦找到目标,所用的步数(或路径长度)一定是最短的。
算法实现步骤
BFS通常使用一个队列(Queue) 这种数据结构来辅助实现。队列的特点是“先进先出”(FIFO),这正好符合我们“先访问的节点,其邻居也先被访问”的需求。
步骤分解:
初始化:选择一个起始节点,将其标记为“已访问”。将该起始节点放入队列。
循环执行以下步骤,直到队列为空:
a. 出队:从队列的头部取出一个节点(我们称它为“当前节点”)。
b. 处理:访问该节点(例如,检查它是否是目标节点,或者进行其他操作)。
c. 探索邻居:检查当前节点的所有“未访问”的邻居节点。
* 将每一个未访问的邻居节点标记为“已访问”。
* 将这些邻居节点依次放入队列的尾部。结束:当队列为空时,说明所有从起点可达的节点都已经被访问过了,算法结束。
一个生动的例子
0
/ \
1 2
/ \ \
3 4 5步骤模拟:
| 步骤 | 队列状态 (队首<- ... <-队尾) | 当前节点 | 访问顺序 | 动作说明 |
|---|---|---|---|---|
| 初始 | [0] | - | - | 将起点0放入队列 |
| 1 | [1, 2] | 0 | 0 | 取出0,访问它。将0的未访问邻居1, 2加入队列。 |
| 2 | [2, 3, 4] | 1 | 1 | 取出1,访问它。将1的未访问邻居3, 4加入队列。 |
| 3 | [3, 4, 5] | 2 | 2 | 取出2,访问它。将2的未访问邻居5加入队列。 |
| 4 | [4, 5] | 3 | 3 | 取出3,访问它。3没有未访问的邻居。 |
| 5 | [5] | 4 | 4 | 取出4,访问它。4没有未访问的邻居。 |
| 6 | [] | 5 | 5 | 取出5,访问它。5没有未访问的 |
最终的访问顺序(BFS遍历序列)是:0, 1, 2, 3, 4, 5。你可以看到,这正是一层一层输出的结果。
BFS的特点和应用场景
特点:
完备性:如果解存在,BFS一定能找到。
最优性:在无权图中,BFS找到的路径一定是最短路径。
空间复杂度高:在最坏情况下,需要存储一整层的节点,对于分支因子为b的树,第d层有b^d个节点,空间复杂度为O(b^d)。
应用场景:
图的连通性:判断两个节点是否连通。
最短路径:在无权图中求两点间的最短路径。
迷宫求解:找到从起点到终点的最短路径。
社交网络:查找“度”关系(例如,寻找三度好友)。
序列变换(如单词接龙问题)。
树的层序遍历。
BFS 在树结构的应用
层序遍历

解析:采用深度优先搜索,但难点是不知道每层具体有多少结点,也就不知道要把多少结果放在数组的同一行,解决方法是在遍历队列之前用一个变量先记录一下队列的长度,然后执行长度次访问队头的操作,执行完后,再次记录队列的长度,下一次遍历队列时就访问长度次......以此类推。
class Solution {
public:
vector> levelOrder(Node* root) {
queue q;
vector> ret;
if(root) q.push(root);
int i = 0;
while(!q.empty())
{
ret.resize(i + 1); // 为下一次记录结果开辟空间
int sz = q.size(); // 记录这一层的结点个数
while(sz--)
{
// 访问对头
ret[i].push_back((q.front())->val);
// 把对头的子结点加入队列
for(auto j : (q.front())->children)
{
q.push(j);
}
// 对头已经访问完了,出队列
q.pop();
}
i++;
}
return ret;
}
}; 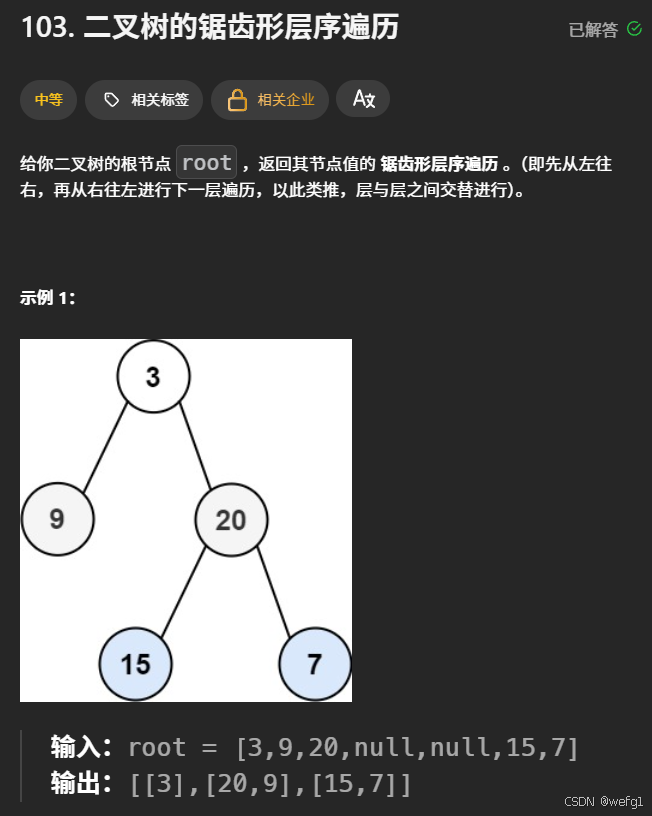
解析:先进行二叉树的层序遍历,最后将结果数组的对应部分进行逆序
class Solution {
public:
vector> zigzagLevelOrder(TreeNode* root) {
vector> ret;
queue q;
int sz = 0;
int i = 0;
if(root) q.push(root);
while(!q.empty())
{
sz = q.size();
ret.resize(i + 1);
while(sz--)
{
TreeNode* top = q.front();
ret[i].push_back(top->val);
q.pop();
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
i++;
}
for(int j = 1; j < ret.size(); j += 2)
{
reverse(ret[j].begin(),ret[j].end());
}
return ret;
}
}; 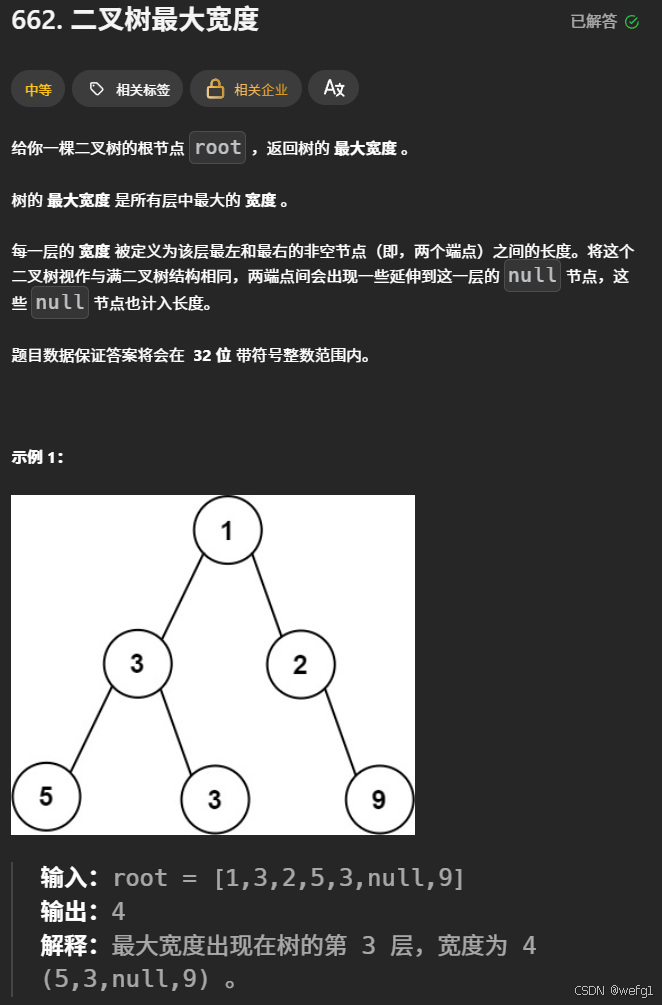
解析:以从左到右,从上到下,从根结点开始为 1,依次对非空结点进行编号,可以发现如果根结点的编号为 n ,那么它的左孩子和右孩子的编号分别为 2*n 和 2*n + 1,树某行的宽度 = 最右边的结点编号 - 最左边结点编号 + 1。对树进行层序遍历,队列中每个元素存储结点和结点的编号。
lass Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
queue> q;
if(root) q.push(make_pair(root,1));
unsigned maxlen = 0;
while(!q.empty())
{
pair front = q.front();
pair back = q.back();
if(back.second - front.second + 1 > maxlen)
maxlen = back.second - front.second + 1;
int sz = q.size();
while(sz--)
{
pair front = q.front();
if((front.first)->left)
q.push(make_pair((front.first)->left,front.second * 2));
if((front.first)->right)
q.push(make_pair((front.first)->right,front.second * 2 + 1));
q.pop();
}
}
return maxlen;
}
}; 



 浙公网安备 33010602011771号
浙公网安备 33010602011771号