目录
树结构
一、Huffman树(最优二叉树)
1、基本概念
(1)路径长度:路径上的分支数目
(2)树的路径长度:从树根到每一结点的路径长度之和
(3)带权路径长度:结点到根的路径长度与结点上权的乘积
(4)树的带权路径长度:树中所有叶子结点的带权路径长度之和
2、Huffman树的定义
哈夫曼树(Huffman Tree),又称最优二叉树,是一类带权路径长度(Weighted Path Length, WPL)最短的二叉树,其核心特性是:对于给定的一组带权值的叶子节点,通过特定特定构造方法使树的总带权路径长度最小。哈夫曼树是 “最优树” 的典型代表,广泛应用于数据压缩、编码等领域。
核心概念:
使该值最小。就是(1)带权路径长度(WPL)指树中所有叶子节点的权值与该节点到根节点的路径长度(边的数量)的乘积之和,公式为:WPL=∑i=1n(wi×li)其中,wi 是第 i 个叶子节点的权值,li 是该叶子节点到根节点的路径长度。哈夫曼树的目标
(2)叶子节点与非叶子节点哈夫曼树中,权值仅存在于叶子节点,非叶子节点的权值由其左右子树的权值之和构成(用于构建树的中间过程)。
3、构建哈夫曼算法
哈夫曼树经过贪心策略构建,步骤如下:
(1)初始化:将所有带权值的叶子节点视为独立的单节点树,组成一个森林(集合)。
(2)迭代合并:
① 从森林中选取权值最小的两棵树,作为新树的左、右子树(左、右顺序不影响 WPL,通常权值小的放左)。
② 新树的根节点权值为两棵子树的权值之和。
③ 将新树加入森林,同时移除参与合并的两棵树。
(3)终止条件:当森林中只剩下一棵树时,该树即为哈夫曼树。
代码示例:
class HuffmanNode:
"""哈夫曼树节点类"""
def __init__(self, weight, char=None, left=None, right=None):
self.weight = weight # 节点权重(叶子节点为字符频率,非叶子节点为子树权重和)
self.char = char # 叶子节点对应的字符(非叶子节点为None)
self.left = left # 左子树
self.right = right # 右子树
# 定义比较方法,用于优先队列排序(按权重从小到大)
def __lt__(self, other):
return self.weight < other.weight
def build_huffman_tree(char_weights):
"""
构建哈夫曼树
:param char_weights: 字符-权重字典(如 {'A':5, 'B':9, ...})
:return: 哈夫曼树的根节点
"""
import heapq # 利用堆实现优先队列,高效获取最小权重节点
# 1. 初始化:将所有字符转为叶子节点,加入优先队列(小根堆)
heap = []
for char, weight in char_weights.items():
node = HuffmanNode(weight, char)
heapq.heappush(heap, node)
# 2. 迭代合并:每次取两个最小权重节点,合并为新节点
while len(heap) > 1:
# 取出权重最小的两个节点
left_node = heapq.heappop(heap)
right_node = heapq.heappop(heap)
# 构建新节点(权重为两节点之和,无字符)
merged_weight = left_node.weight + right_node.weight
merged_node = HuffmanNode(merged_weight, left=left_node, right=right_node)
# 将新节点加入优先队列
heapq.heappush(heap, merged_node)
# 3. 剩余的最后一个节点即为哈夫曼树的根节点
return heap[0] if heap else None
def calculate_wpl(root, depth=0):
"""计算哈夫曼树的带权路径长度(WPL)"""
if root is None:
return 0
# 叶子节点:累加 权重×深度
if root.left is None and root.right is None:
return root.weight * depth
# 非叶子节点:递归计算左右子树的WPL之和
return calculate_wpl(root.left, depth + 1) + calculate_wpl(root.right, depth + 1)
# 示例使用
if __name__ == "__main__":
# 字符及其频率(权重)
char_weights = {'A': 5, 'B': 9, 'C': 12, 'D': 13, 'E': 16, 'F': 45}
# 构建哈夫曼树
huffman_root = build_huffman_tree(char_weights)
# 计算WPL
wpl = calculate_wpl(huffman_root)
print(f"哈夫曼树的带权路径长度(WPL):{wpl}") # 输出:269(与之前示例一致)4、示例说明
示例1:给定叶子节点权值:[5, 9, 12, 13, 16, 45],构建哈夫曼树的过程:
(1)初始森林:{5, 9, 12, 13, 16, 45}。
(2)第一次合并:选最小的 5 和 9,合并为根权值 14 的树,森林变为 {12, 13, 14, 16, 45}。
(3)第二次合并:选 12 和 13,合并为根权值 25 的树,森林变为 {14, 16, 25, 45}。
(4)第三次合并:选 14 和 16,合并为根权值 30 的树,森林变为 {25, 30, 45}。
(5)第四次合并:选 25 和 30,合并为根权值 55 的树,森林变为 {45, 55}。
(6)第五次合并:选 45 和 55,合并为根权值 100 的树,森林只剩一棵树,即哈夫曼树。
最终树的 WPL 计算:5×4+9×4+12×3+13×3+16×3+45×2=20+36+36+39+48+90=269,为所有可能二叉树中最小的 WPL。
示例2:

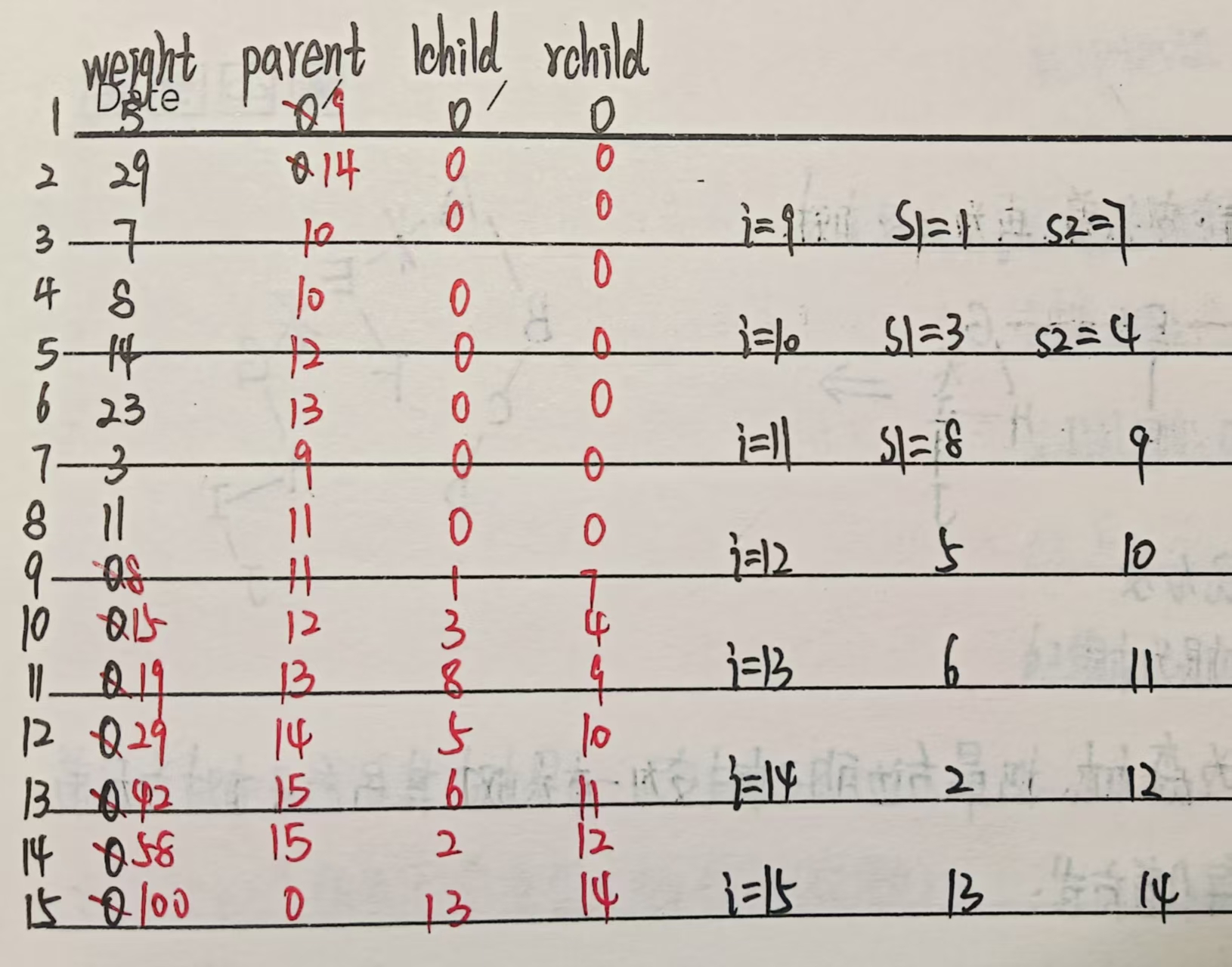
5、结构特点
(1)权值越大的叶子节点,距离根节点越近(贪心策略的体现,减少高权值节点的路径长度)。
(2)没有度为 1 的节点(所有非叶子节点均有左右子树,即 “严格二叉树”)。
(3)若叶子节点数量为 n,则哈夫曼树的总节点数为 2n−1(因每次合并增加 1 个节点,共需 n−1 次合并)。
6、应用:哈夫曼编码
哈夫曼树的典型应用是哈夫曼编码(数据压缩算法),原理如下:
(1)对字符(叶子节点)按出现频率(权值)构建哈夫曼树。
(2)从根到叶子的路径中,左分支标记为 “0”,右分支标记为 “1”,叶子节点的路径编码即为该字符的哈夫曼编码。
(3)特性:高频字符编码短,低频字符编码长,且编码无歧义(前缀编码,任一编码不是其他编码的前缀),从而实现高效压缩。
二、哈夫曼编码的简单介绍
1、哈夫曼编码的定义
哈夫曼编码是基于哈夫曼树(最优二叉树)的一种前缀编码,核心是为高频字符分配短编码、低频字符分配长编码,从而实现信息的高效压缩,且无编码歧义。
2、核心原理
(1)以频率为权值构建哈夫曼树将得编码的字符视为 “叶子节点”,其出现频率作为节点 “权值”,按哈夫曼树的构建规则(反复合并权值最小的两棵树)生成哈夫曼树。
(2)路径即编码从哈夫曼树的根节点出发,向左子树走标记为 “0”,向右子树走标记为 “1”;每个叶子节点(字符)从根到自身的路径序列,就是该字符的哈夫曼编码。
3、关键特性
(1)前缀编码:任一字符的编码都不是其他字符编码的前缀,避免解码时产生歧义。例如 “01” 和 “010” 不能同时存在,基于前者是后者的前缀。
(2)压缩高效:高频字符编码短、低频字符编码长,整体编码总长度最短,压缩率高于固定长度编码(如 ASCII 码)。
4、简单示例
假设字符及出现频率如下:
| 字符 | A | B | C | D |
|---|---|---|---|---|
| 频率 | 5 | 9 | 12 | 13 |
(1)构建哈夫曼树:按频率(权值)合并,最终生成哈夫曼树(过程参考哈夫曼树构建)。
(2)生成编码:
① A(频率 5):路径为 “000”,编码 = 000
② B(频率 9):路径为 “001”,编码 = 001
③ C(频率 12):路径为 “01”,编码 = 01
④ D(频率 13):路径为 “1”,编码 = 1
(3)编码与解码:原文 “ABDC” 的编码为 “000 001 1 01”(合并后为 “000001101”);解码时,从根出发按 “0/1” 路径找叶子节点,即可还原为原字符。
5、应用场景
无损数据压缩的基础,广泛用于:就是哈夫曼编码
(1)材料压缩格式(如 ZIP、GZIP)。
(2)图像压缩(如 JPEG 的 entropy coding 阶段)。
(3)通信传输中的数据编码,减少传输带宽。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号