磁共振成像原理（理论）21：K空间采样 (Sampling of k-Space) - k空间信号的采样要求 - 详解

一个多维采样困难。然而，在实践中，通常分别处理每个维度上的采样，从而将其简化为一维采样问题。由此产生的采样模式并非最优，但它保证了底层连续就是k空间的采样 $k$ 空间信号的“完美”重建。因此，大家采用这种常规处理方法来确定两种流行成像方案（直角坐标采样和极坐标采样）的MRI数据采集参数的采样要求。这里我们只考虑二维成像，因为如果需要，可以轻松地将处理办法扩展到更高维的情况。

我们首先考虑直角坐标采样的情况。假设被成像的物体被一个宽度为 $W_x$ 和 $W_y$ 的矩形所限定，如下图所示。那么，根据采样定理，在 $k$ 空间中的采样间隔需满足：
$\Delta k_x \leq \frac{1}{W_x} \quad \text{和} \quad \Delta k_y \leq \frac{1}{W_y} \tag{5.122}$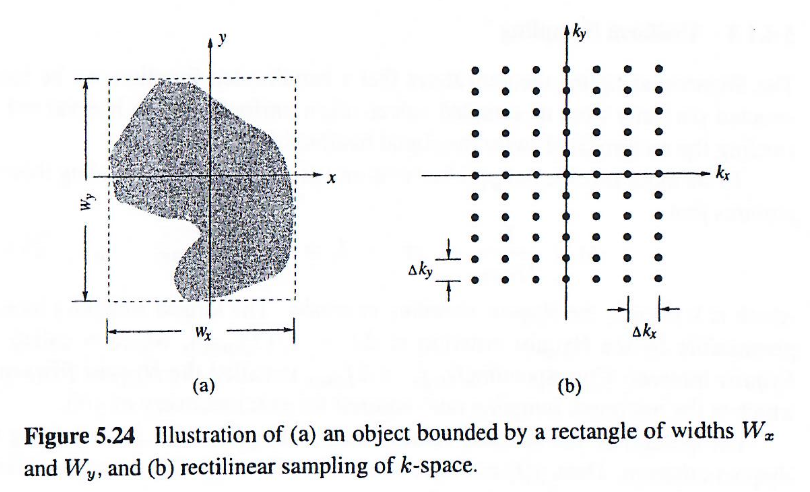

我们进一步假设沿 $x$ 方向使用频率编码，沿 $y$ 方向利用相位编码。那么， $k$ 空间的采样间隔与序列参数的关系为：
$\begin{cases} \Delta k_x = \gamma |G_x| \Delta t \\ \Delta k_y = \gamma \Delta G_y T_{pe} \end{cases} \tag{5.123}$

其中：

$G_x$ ：频率编码梯度
$Δt\Delta t$ ：读出采样时间间隔
$ΔGy\Delta G_y$ ：相位编码梯度步长
$T_{pe}$ ：相位编码时间间隔

将方程 (5.123) 代入方程 (5.122)，大家立即得到对数据采集参数的以下要求：
$\begin{cases} \Delta t \leq \frac{2\pi}{\gamma |G_x| W_x} \\ \Delta G_y \leq \frac{2\pi}{\gamma T_{pe} W_y} \end{cases} \tag{5.124}$

接下来我们考虑极坐标采样的情况，如下图所示。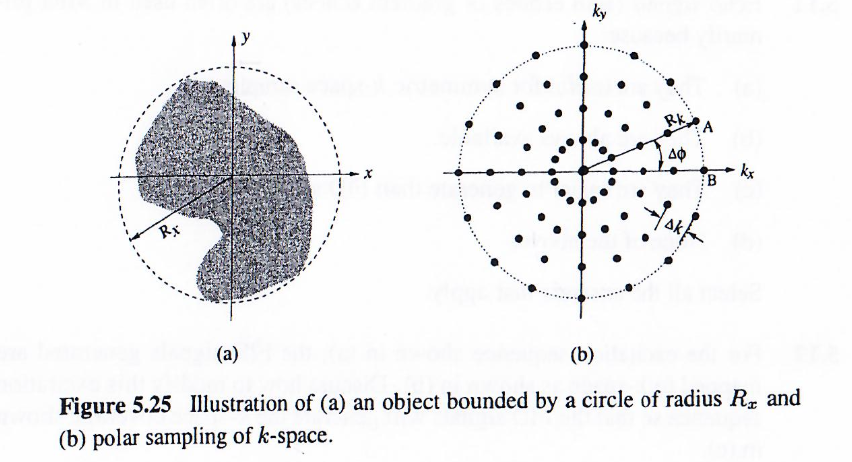

在这种成像方案中，有两个基本的数据采集参数： $Δk\Delta k$ 和 $Δϕ\Delta \phi$ 。为了获得对这些参数的要求，需要做出以下两个标准假设：

(a) 空间有限性：
$\rho(x, y) = 0 \quad \text{当} \quad \sqrt{x^2 + y^2} \geq R_x \tag{5.125}$

(b) 频率有限性：
$S(k_x, k_y) = \mathcal{F}{\rho\\} = 0 \quad \text{当} \quad \sqrt{k_x^2 + k_y^2} \geq R_k \tag{5.126}$

第一个假设是有效的，因为实际物体的函数是空间有限的。第二个假设只是一个近似，因为一个函数不可能同时是空间和频率有限的。然而，该假设是必要的，它使我们能够推导出沿 $ϕ\phi$ 方向的最小采样要求。

根据假设 (a)，对于每个固定的 $ϕ\phi$ ，沿 $k$ 通过方向的采样要求能够很容易地确定。具体来说，容易证明：
$\Delta k = \gamma G \Delta t \leq \frac{1}{2 R_x} \tag{5.127}$

或者
$\Delta t \leq \frac{\pi}{\gamma G R_x} \tag{5.128}$

其中 $\sqrt{G_x^2 + G_y^2}$ 。

确定沿 $ϕ\phi$ 方向的最小采样要求比确定沿 $k$ 方向的要求更为复杂。因为对于给定的 $k$ ， $Sp(k,ϕ)S_p(k, \phi)$ 是 $ϕ\phi$ 的周期函数，大家可以用傅里叶级数将其表示为：
$S_p(k, \phi) = \sum_{n=-\infty}^{\infty} c_n(k) e^{-i n \phi} \tag{5.129}$

其中
$c_n(k) = \frac{1}{2\pi} \int_{-\pi}^{\pi} S_p(k, \phi) e^{i n \phi} d\phi \tag{5.130}$

方程 (5.129) 中傅里叶级数的重要项数决定了 $Sp(k,ϕ)S_p(k, \phi)$ 所允许的最大角度采样间隔 $Δϕ\Delta \phi$ 。对于一个圆对称的物体， $Sp(k,ϕ)S_p(k, \phi)$ 在 $ϕ\phi$ 上是常数，该级数将只有一个直流项。通常，重要项的数量随着 $∣ k ∣$ 的增加而增加。

关于这个问题的一个结果在《Sampling the 2-D Radon Transform》中给出，该结果指出 $Sp(k,ϕ)S_p(k, \phi)$ 相对于 $ϕ\phi$ 是带限的，其带宽为 $Rx2π∣k∣+1R_x 2\pi |k| + 1$ 。换句话说，方程 (5.129) 中的傅里叶级数系数 $c_n(k)$ 对于 $[R_x 2\pi |k|] + 1$ 是不核心的，其中方括号表示将 $Rx2π∣k∣R_x 2\pi |k|$ 四舍五入到下一个更高的整数。基于方程 (5.126) 中所述的频率有限性假设，如果 $[2\pi R_x R_k] + 1$ ，则对于任何测量的 $k$ 值， $c_n$ 都可以被忽略。因此，根据带限周期函数采样的结果，对于所有采样的 $k$ 值满足奈奎斯特准则的角度采样间隔由下式给出：
$\Delta \phi \leq \frac{2\pi}{2([2\pi R_x R_k] + 1) + 1} \tag{5.131}$

基于方程 (5.131) 可以推导出一个更有指导意义的关系，它将径向线的数量（或投影数），记为 $NϕN_\phi$ ，直接与每条线上的样本数，记为 $N_k$ ，联系起来。更具体地说，考虑到在 $\Delta \phi$ 和 $\Delta \phi + \pi$ 同时采集的，我们可以将就是处的信息 $NϕN_\phi$ 表示为：
$N_\phi = \frac{\pi}{\Delta \phi} \geq [2\pi R_x R_k] + 1.5 \tag{5.132}$

用以下关系式替换 $R_x$ 和 $R_k$ ：
$R_x = \frac{1}{2 \Delta k} \tag{5.133}$
和
$R_k = \frac{N_k}{2} \Delta k \tag{5.134}$

我们立即得到：
$\frac{N_\phi}{N_k} \approx \frac{\pi}{2} \tag{5.135}$

方程 (5.135) 表明，所需的投影数大致等于每个投影的样本数。

有趣的是，方程 (5.135) 的结果也可以凭借将最差情况的方位角分辨率和径向分辨率设置为大致相同来获得。观察上图可知，最差情况的方位角分辨率由下式给出：
$\overline{AB} = \Delta \phi R_k = \frac{\pi}{N_\phi} \frac{N_k}{2} \Delta k \tag{5.136}$

令 $AB‾≈Δk\overline{AB} \approx \Delta k$ 立即得到方程 (5.135)。

到目前为止，我们一起推导了从微观磁矩 $μ⃗\vec{\mu}$ 到 $k$ 空间数据 $S(k⃗)S(\vec{k})$
$\vec{\mu}\longrightarrow\vec{M}\longrightarrow\vec{M}_{xy}\longrightarrow S(t)\longrightarrow S(\vec{k})$

在后面的分享中，会重点关注，如何由 $k$ 空间数据 $S(k⃗)S(\vec{k})$ 到图像 $I(x⃗)I(\vec{x})$
$S(\vec{k})\longrightarrow I(\vec{x})$

期待在后续的分享中再见。

发表于 2025-11-07 14:21 jzssuanfa 阅读(22) 评论(0) 收藏举报

刷新页面返回顶部

磁共振成像原理（理论）21：K空间采样 (Sampling of k-Space) - k空间信号的采样要求 - 详解

导航