目录
一、参数与结构
参数与结构主要是包含:
网络层数
不同隐含层个数
不同激活函数(隐含层的Sigmoid() 函数,Relu() 函数。注:输出层是统一的softmax()函数))
不同超参数(包含随机初始化权重值,学习率,训练(迭代)次数)
优化方法
二、网络层数
2.1 网络层数:
越来越深,输入层和输出层神经元个数不变,一个输入层一个输出层。保持学习率,隐含层神经元个数,激活函数、初始化权重值,训练次数不变。
| layer | 结果 |
|---|---|
| [784, 100, 10] | 收敛过程
|
| 学习结果
|
| 泛化能力 | |
| [784, 100, 75, 10] | 收敛过程:
|
| 学习结果
|
| 泛化能力 | |
| [784, 100, 75, 50,10] | 收敛过程
|
| 学习结果
| |
| 泛化能力 |
结论:网络越深,收敛的越慢,一定的深度增加测试集合的准确率和验证集的准确率。
2.2 不同隐含层神经元个数
增加隐含层神经元的个数,使用四层网络的结构,保持训练次数500,学习率0.01,使用relu激活函数。
| layer | 结果 |
|---|---|
| [784, 100, 75, 10] | 收敛过程
|
| 学习结果
| |
| 泛化能力 | |
| [784, 200, 150, 10] | 收敛过程
|
| 学习结果
| |
| 泛化能力 | |
| [784, 300,225,10] | 收敛过程
|
| 学习结果
| |
| 泛化能力 |
结论:随着隐含层的神经元个数的增加,
2.3 不同激活函数
(1)Sigmoid() 函数:
函数表达式:Sigmoid(x)=\frac{1}{1+e^{-x}}
代码实现:
def sigmoid(Z):
A = 1/(1+np.exp(-Z))
cache = Z
return A, cache其导函数为:f(x)=1+e−x1=ex+1ex=1−(ex*+1)−1
代码实现:
def sigmoid_backward(dA, cache):
Z = cache
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1-s)
return dZ(2)Relu() 函数:
函数表达式:f\left( x \right) \,\,=\,\,Max\left( 0,x \right) 代码实现:
def relu(Z):
A = np.maximum(0,Z)
cache = Z
return A, cache其导函数为: f\left( x \right) ' =\,\,\begin{cases} 0 , x\,\,=\,\,0;\\ 1 , x\,\,\ne \,\,0;\\ \end{cases}
代码实现:
def relu_backward(dA, cache):
Z = cache
dZ = np.array(dA, copy=True)
dZ[Z <= 0] = 0
return dZ(3) 两个激活函数的对比
再相同的网络结构、参数下进行训练:[784, 100, 75, 10]
结果:
| relu() | sigmoid() | |
|---|---|---|
|
| |
| 收敛过程: |
|
|
| 学习结果与泛化能力: |
|
|
总结:一开始sigmoid()函数收敛快,但是到某一点的时候,收敛速度陡然下降,并几乎为一个常数。relu()函数则从开始到最后都保持一个很好的稳定性。且在MINIST数据集上,sigmod函数效果比relu函数的差。
2.4 不同超参数
(1)随机初始化权重值 (通过改变np.random.seed(3)随机种子值来设置初始化权重参数)
def init_W(layers_dims):
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for l in range(1, L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1])
parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
return parameters(2)学习率
改变代码中的learning_rate=0.0075(默认),改变学习率。
def deepnet(X, Y,net_layers,learning_rate=0.0075, num_iterations=3000,step =1, print_cost=False, isPlot=True):
np.random.seed(1) #设计种子
costs = [] #用于画图
parameters = init_W(net_layers)
for i in range(0, num_iterations):
# 迭代
AL, caches = L_forword(X, parameters)
costi = cost(AL, Y) #这里的Y是标准化的Y
grads = L_model_backward(AL, Y, caches,"softmax")
parameters = update_parameters(parameters, grads, learning_rate)
if i % step == 0:
# 记录成本
costs.append(costi)
# 是否打印成本值
if print_cost:
print("第", i, "次迭代,成本值为:", np.squeeze(costi))
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# plt.savefig(fnme = "cast"+str(datetime.datetime.now())+".jig")
return parameters使用网络结构为[784, 50,35,10],500的迭代次数。
| learning_rate | 结果 |
|---|---|
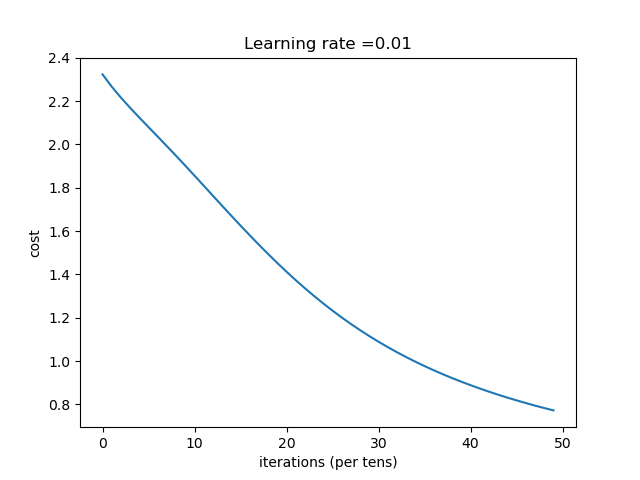
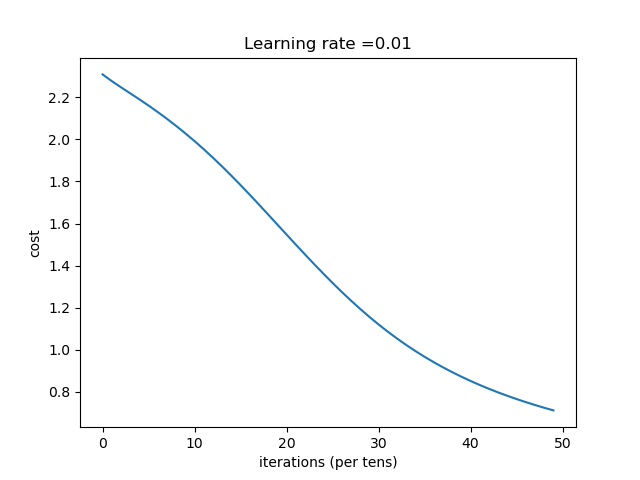
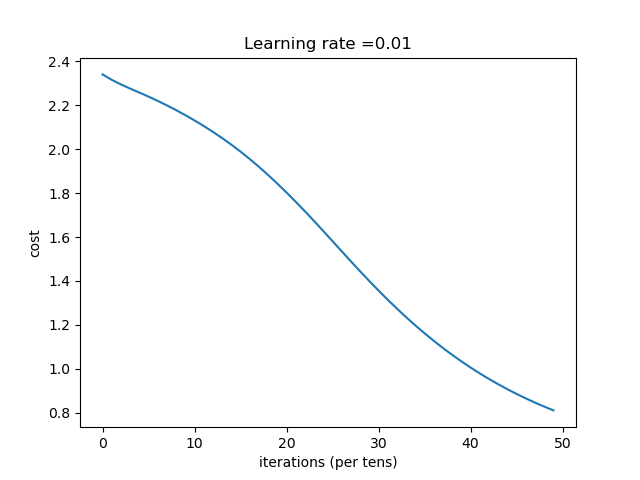
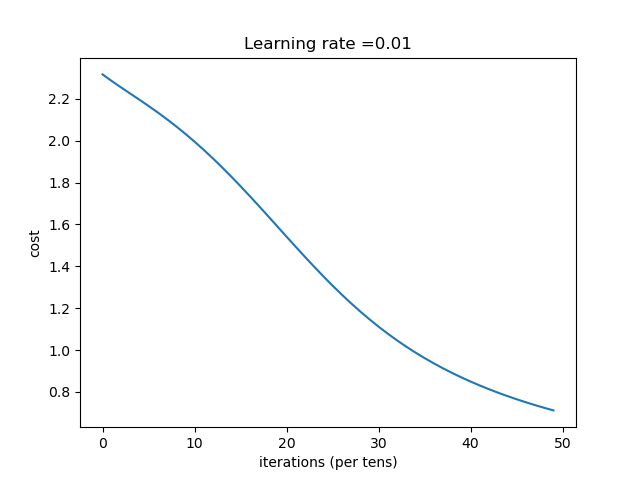
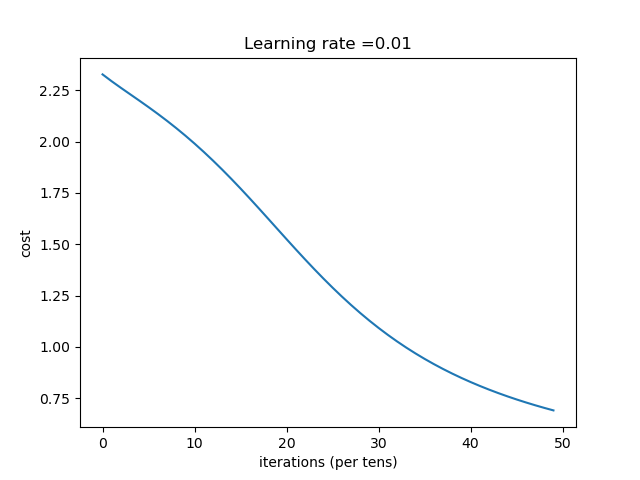
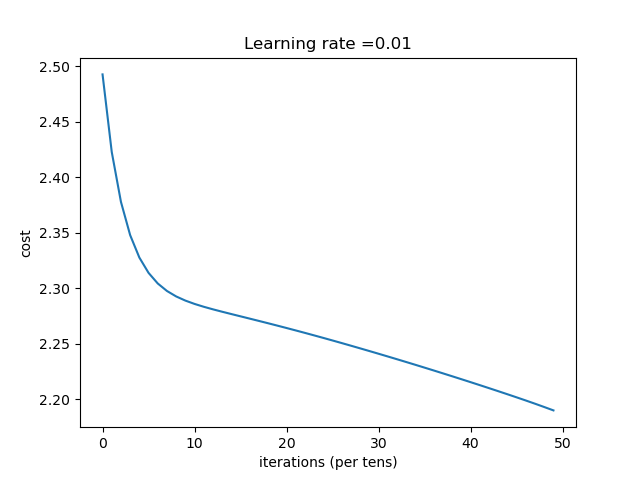
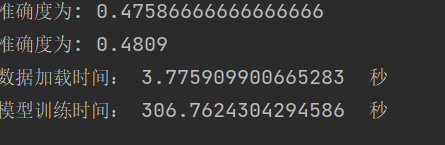
| 0.01 | 收敛过程
|
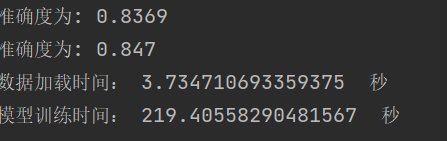
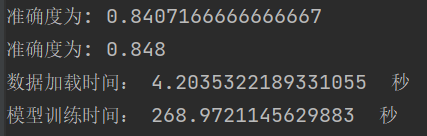
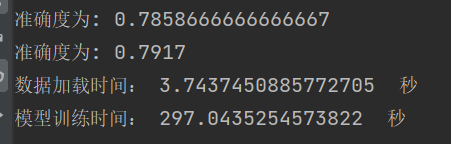
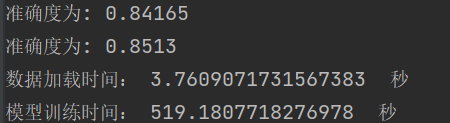
| 学习结果
| |
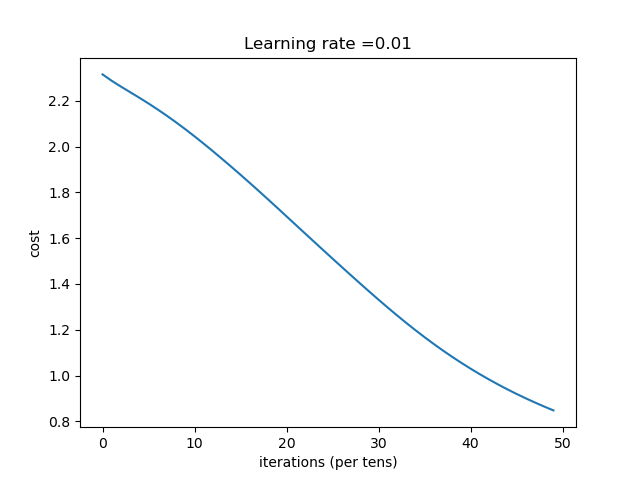
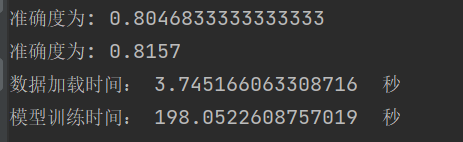
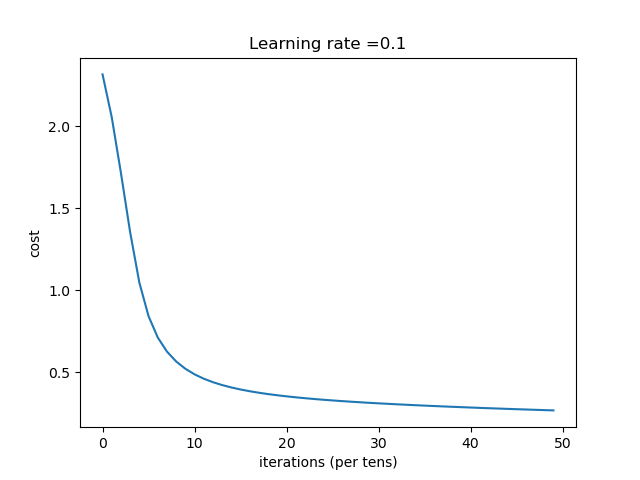
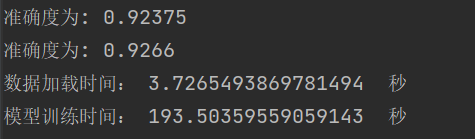
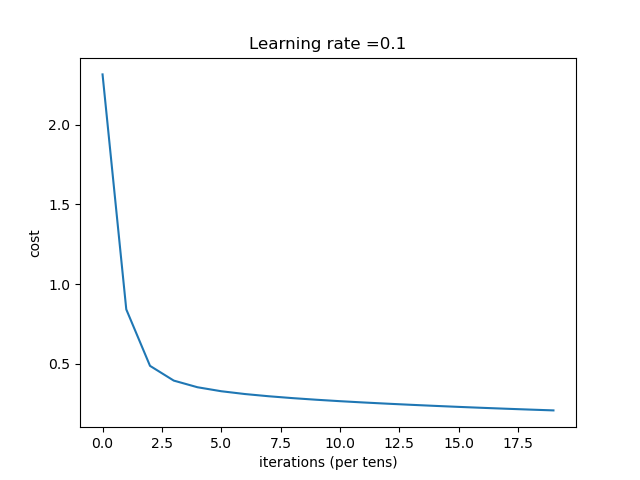
| 0.1 | 收敛过程
|
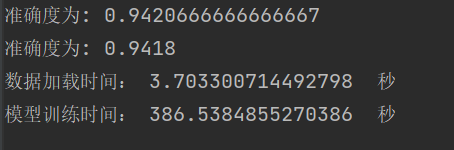
| 学习结果与泛化能力
| |
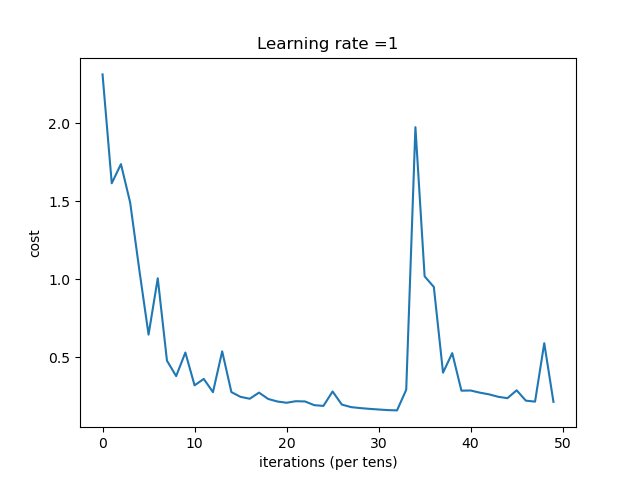
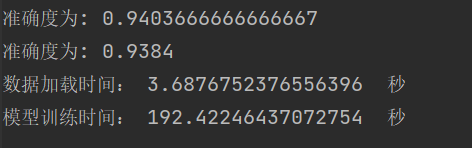
| 1 | 收敛过程
|
| 学习结果泛化能力
| |
总结:学习率选择合适对网络非常重要,过小等于0.01时,收敛慢,过大等于1时导致在最优值左右摆动。
(3)训练(迭代)次数
改变代码中的num_iterations=3000,改变训练(迭代)次数。
def deepnet(X, Y,net_layers,learning_rate=0.0075, num_iterations=3000,step =1, print_cost=False, isPlot=True):
np.random.seed(1) #设计种子
costs = [] #用于画图
parameters = init_W(net_layers)
for i in range(0, num_iterations):
# 迭代
AL, caches = L_forword(X, parameters)
costi = cost(AL, Y) #这里的Y是标准化的Y
grads = L_model_backward(AL, Y, caches,"softmax")
parameters = update_parameters(parameters, grads, learning_rate)
if i % step == 0:
# 记录成本
costs.append(costi)
# 是否打印成本值
if print_cost:
print("第", i, "次迭代,成本值为:", np.squeeze(costi))
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# plt.savefig(fnme = "cast"+str(datetime.datetime.now())+".jig")
return parameters[784, 50,35,10]
| num_iterations | 结果 |
|---|---|
| 500 | 收敛过程 第 490 次迭代,成本值为: 0.21306134142390626
|
| 学习结果
| |
| 泛化能力 | |
| 1000 | 收敛过程 第 950 次迭代,成本值为: 0.2089563048185612
|
| 学习结果
| |
| 泛化能力 |
总结:在正常情况下,随着迭代次数的增多,网络效果越好。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号