Q:聊一下数据结构
所谓的聊一下!就是没错,很多面试官就是这么问的,没有更细节的问题了......就
思考:
如此简单的疑问,简直让人无法开口,到底怎样的回答才能突显出自己的实力呢?
如果回答后,关于数据结构这个问题开始变成了扯皮大战,面试官和自己开始一问一答那么迟早会回答不出来的.
所以我们得一锤定音,一次回答后满足面试官在数据结构这块对自己的所有好奇心,最好是吊打面试官!
方案:
从三个方向来阐述 数据结构 该话题
- 常见的数据结构
与特定语言无关,但是和理论知识储备有关,此处体现自己的知识广度 - 相同数据结构类型中的明显差异
加分项,此处体现自己的知识深度 - Java中达成的数据结构
贴近编码生活,看看java是怎么实现常见的数据结构
常见的数据结构-图示
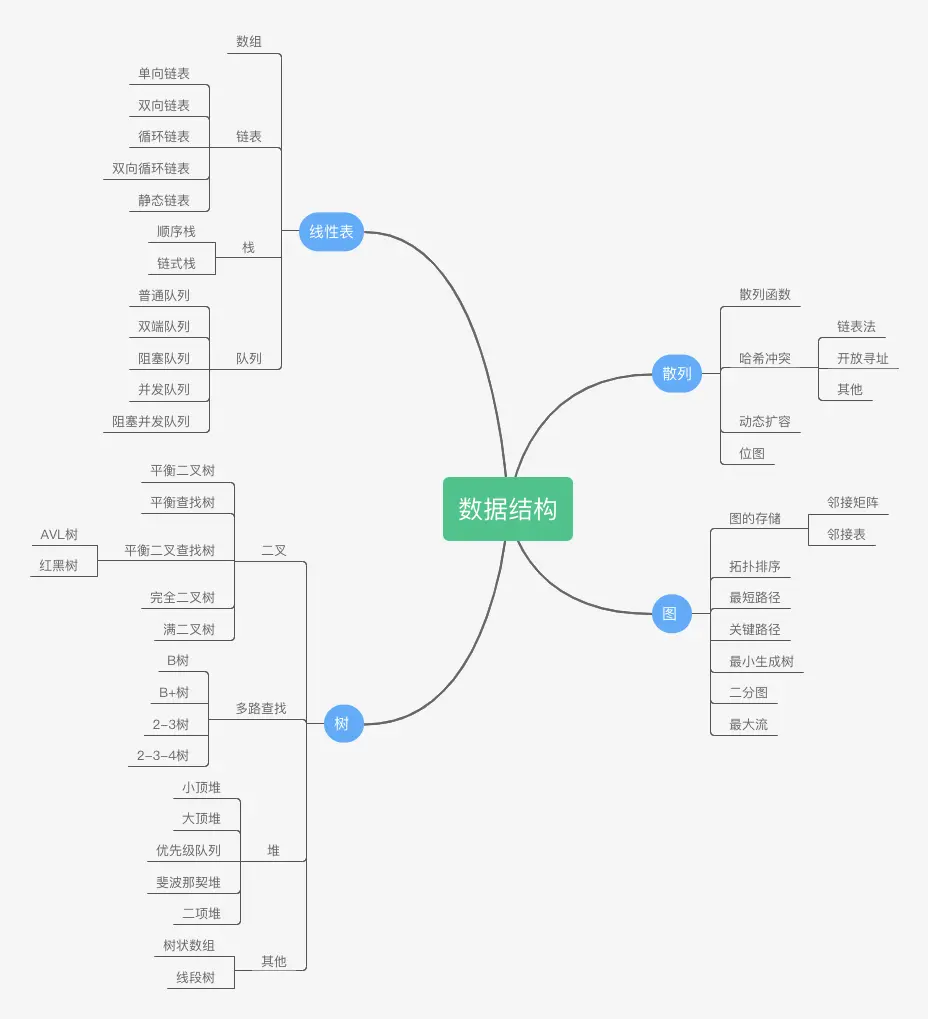
常见的数据结构-图示
常见的数据结构在类型上包括:线性表,散列,树和图.
线性表中常见的数据结构有:数组,链表,栈和队列.
链表又分为单向,双向,循环,双向循环和静态链表.
栈的建立可以用数组实现顺序栈也可以用链表实现为链式栈.
队列有普通队列,双端队列,阻塞队列,并发队列以及阻塞并发队列.
树结构中常见的有二叉树,多路查找树和堆
相同数据结构类型中的明显差异
数组和链表的区别,数组存储需要一块连续的内存空间,对内存要求较高.链表许可使用零散的内存块存储.
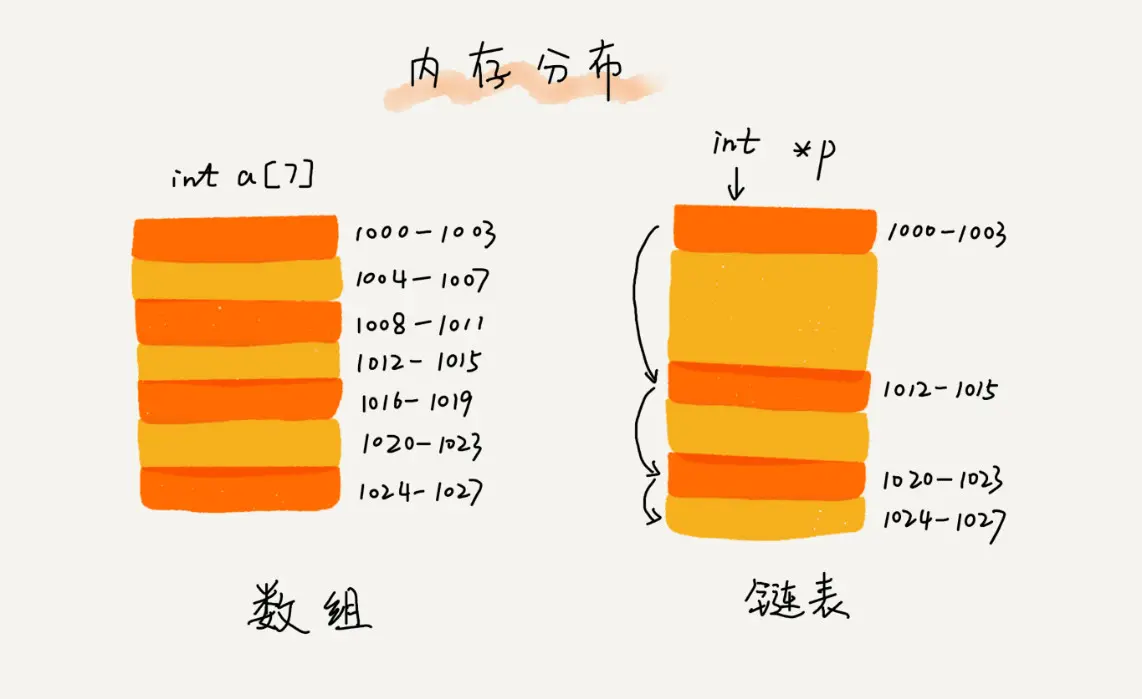
数组和链表性能区别
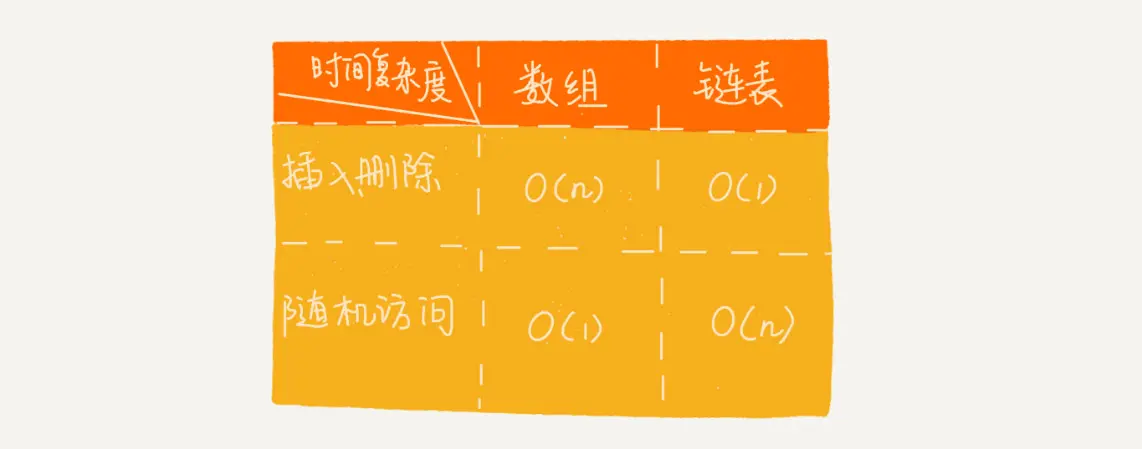
单向链表,双向链表,循环链表,双向循环链表,静态链表的区别.
单向链表中,node中只引用下一个node.
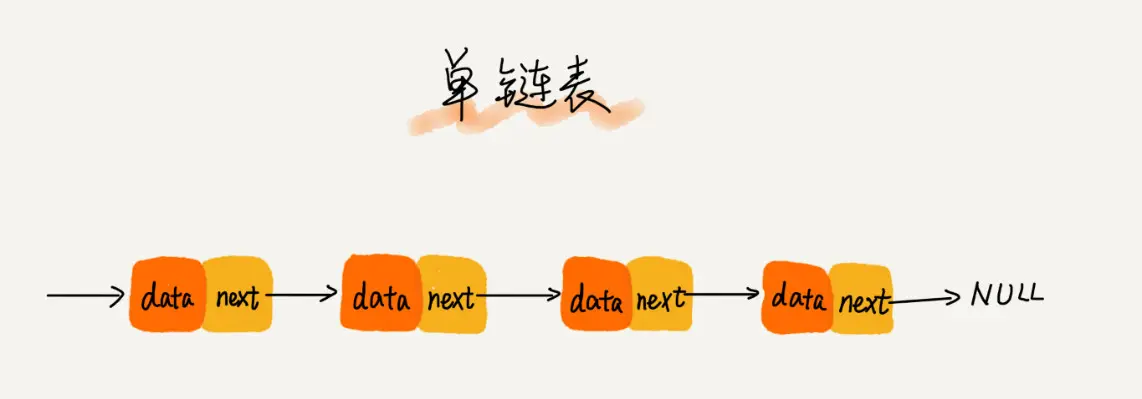
双向链表中,node中引用了上一个和下一个node.
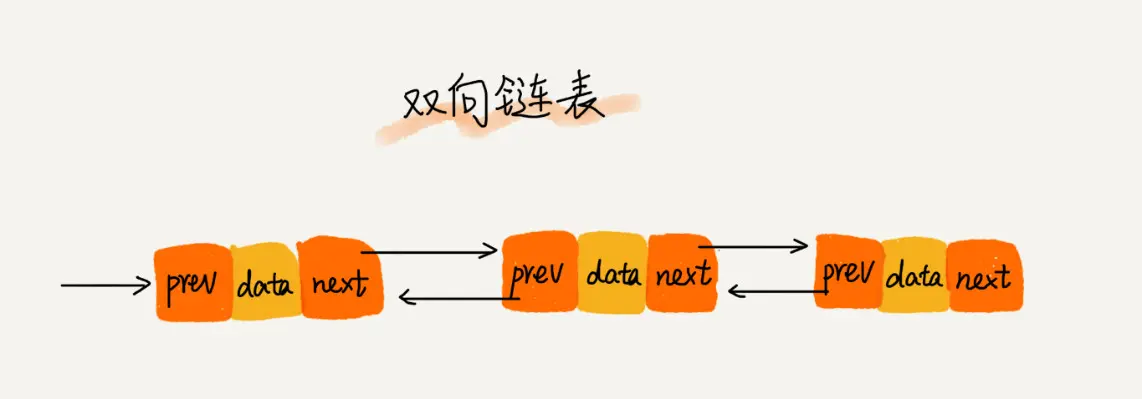
循环链表的最后一个node的下一个node就是头结点.
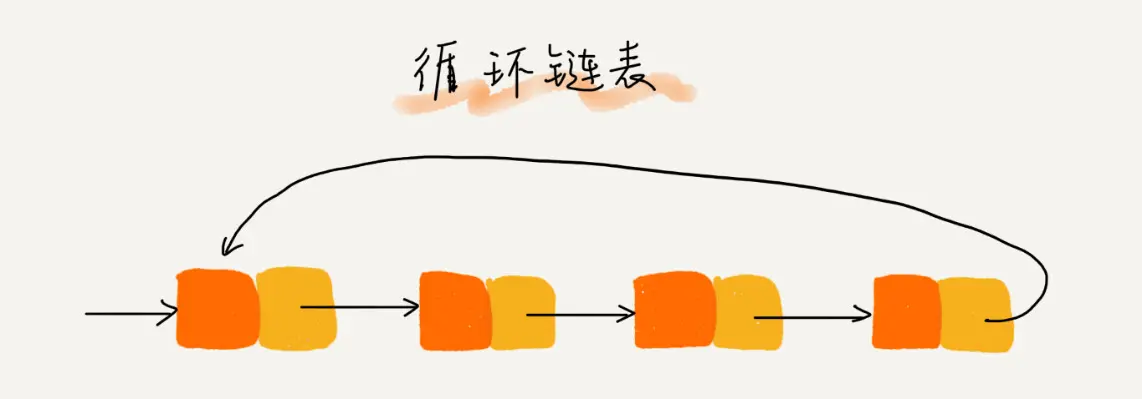
双向循环链表的头结点的上一个结点是尾结点,尾结点的下一个节点是头结点.
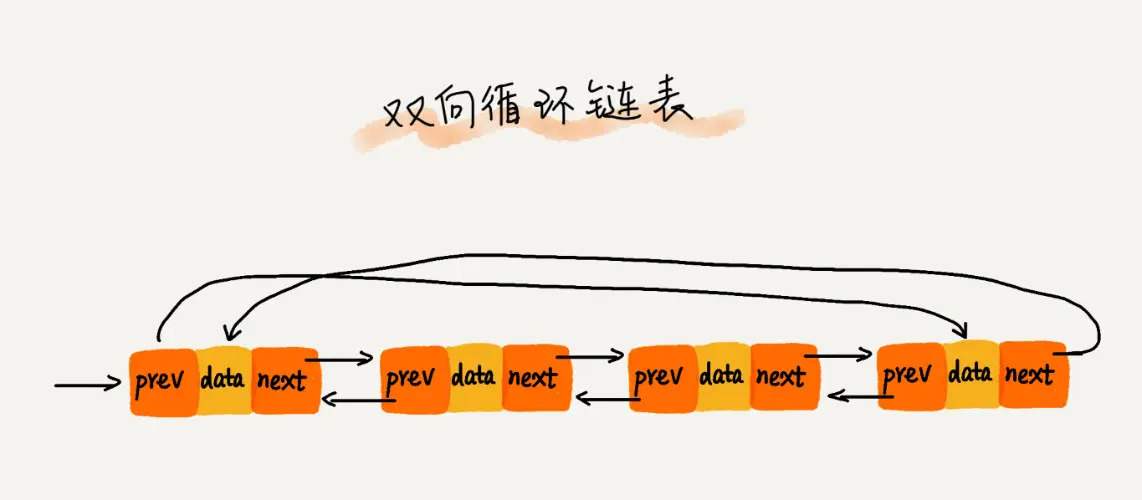
栈: 顺序栈和链式栈的区别
用数组实现的栈,大家叫作顺序栈,用链表建立的栈,我们叫作链式栈。
队列: 普通队列,双端队列,阻塞队列,并发队列,并发阻塞队列
用数组实现的队列叫顺序队列,用链表实现的交链式队列.
顺序队列
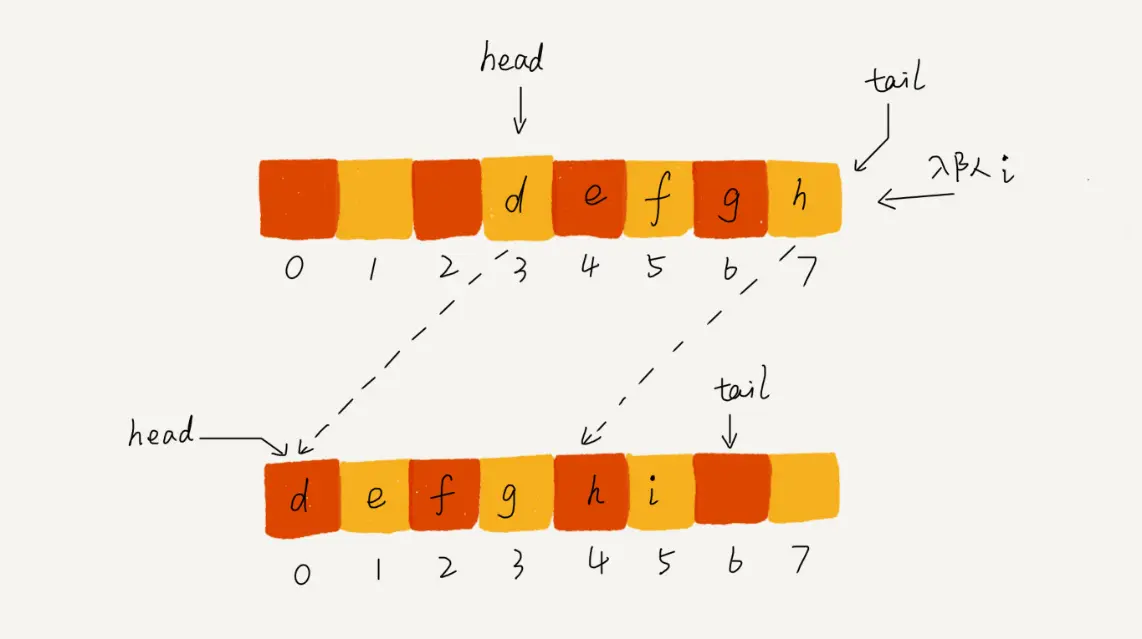
链式队列
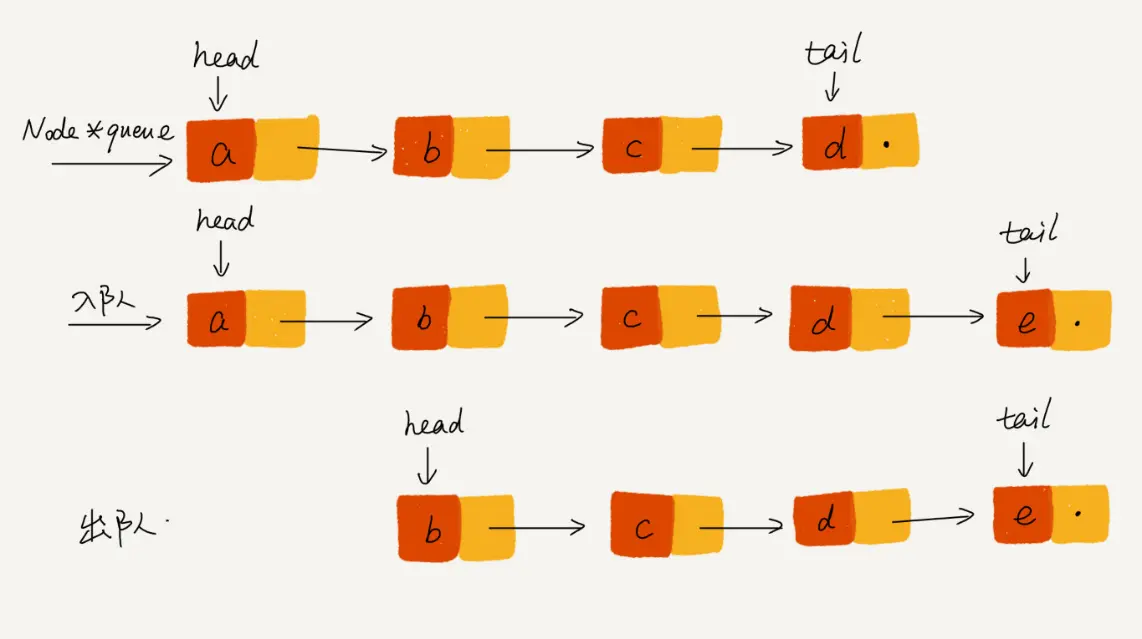
循环队列
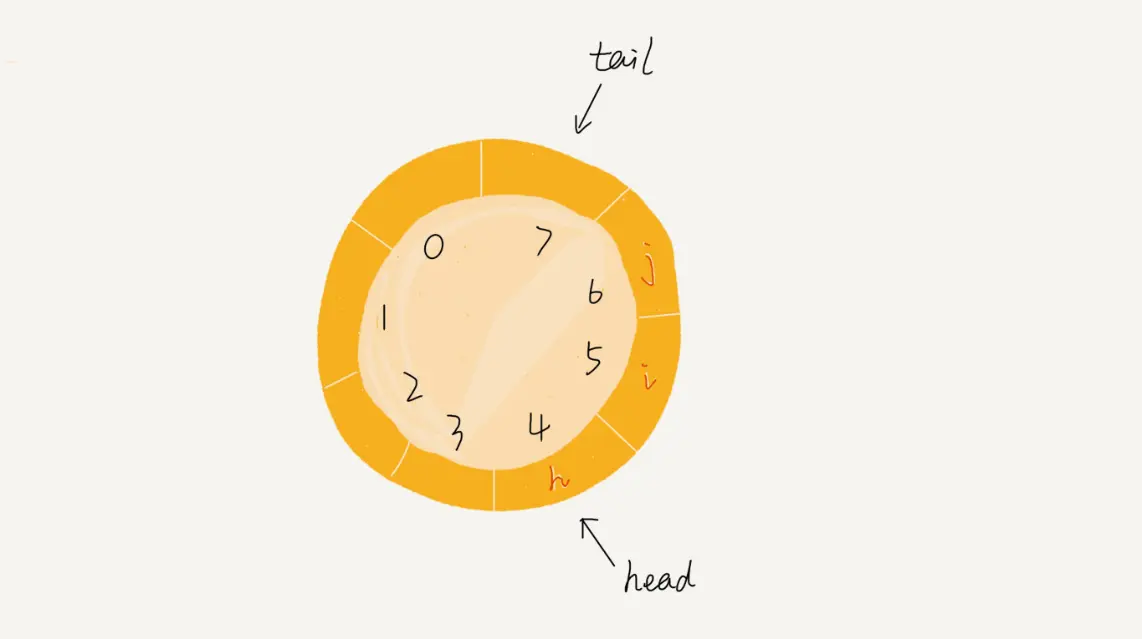
阻塞队列
当队列中元素为空时,进行出队运行将会阻塞,直到有新的元素入队.
当队列中元素满了时,进入入队处理将会阻塞,直到有元素被出队.
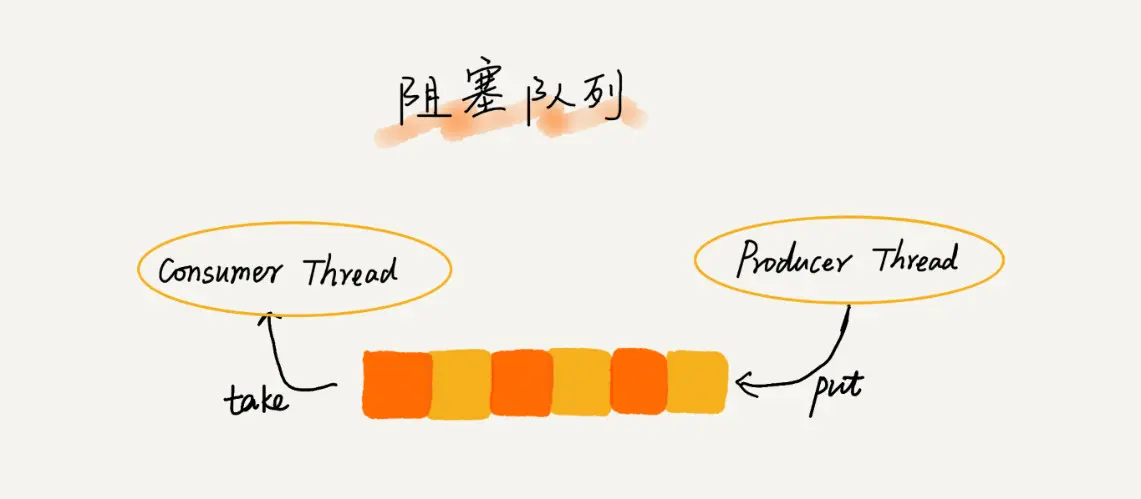
并发队列
基于数组的顺序循环队列在enqueue()和dequeue()上使用CAS原子管理,并发性能十分高效,这也是为什么比链式队列应用更广的原因.
队列满了该怎么办?
可以通过数组搭建一个无界的队列(unbounded queue),将准备入队的元素加入其中,但是这可能会导致大量元素积压,入队和出队时间都很久,对于时间比较敏感的系统是不合适的.
可以通过链表实现一个有界队列bounded queue,有界队列满了时就抛弃元素,但是有界队列过小则无法充分利用系统资源发挥最大性能.
树: 二叉树,多路查找树,堆
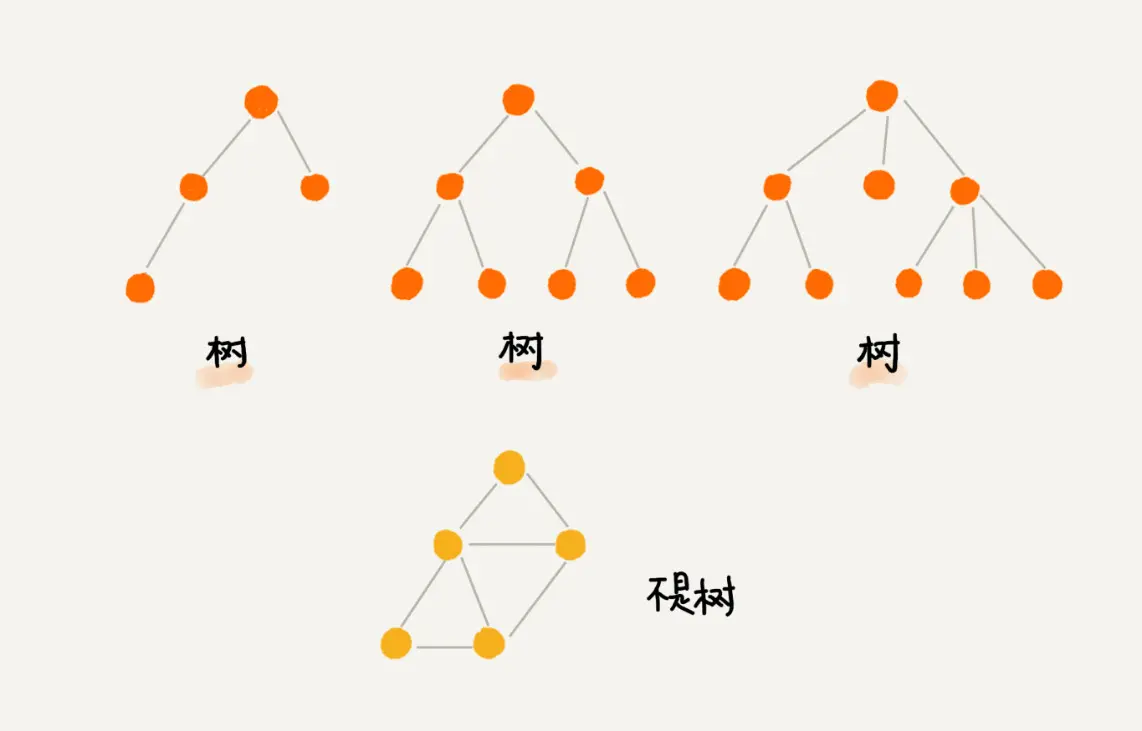
父节点,子节点,兄弟节点,叶节点
A 节点就是 B 节点的父节点,B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点,所以它们之间互称为兄弟节点。我们把没有父节点的节点叫做根节点,也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点,比如图中的 G、H、I、J、K、L 都是叶子节点。
image.png节点高度,深度,层
image.pngimage.png
满二叉树,完全二叉树
编号 2 的二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫做满二叉树。
编号 3 的二叉树中,叶子节点都在最底下两层,最终一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫做完全二叉树image.png
二叉树的存储
链式存储
我们先来看比较简单、直观的链式存储法。从图中你应该允许很清楚地看到,每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。我们只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来。这种存储方式我们比较常用。大部分二叉树代码都是借助这种结构来完成的。image.png
顺序存储
我们再来看,基于数组的顺序存储法。我们把根节点存储在下标 i = 1 的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置。以此类推,B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
总结一下,如果节点 X 存储在数组中下标为 i 的位置,下标为 2 * i 的位置存储的就是左子节点,下标为 2 * i + 1 的位置存储的就是右子节点。反过来,下标为 i/2 的位置存储就是它的父节点。经过此种方式,我们只要知道根节点存储的位置(一般情况下,为了方便计算子节点,根节点会存储在下标为 1 的位置),这样就行通过下标计算,把整棵树都串起来。
不过,刚刚举的例子是一棵完全二叉树,因此仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树,其实会浪费比较多的数组存储空间。image.png完全二叉树适用于使用数组存储,允许做到空间利用最大化,非完全二叉树则会浪费较多数组空间.
image.png
所以,假设某棵二叉树是一棵完全二叉树,那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样,要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因,也是为什么完全二叉树要求最后一层的子节点都靠左的原因。
二叉树的遍历
如何将所有节点都遍历打印出来呢?经典的办法有三种,前序遍历、中序遍历和后序遍历。其中,前、中、后序,表示的是节点与它的左右子树节点遍历打印的先后顺序。
前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,末了打印它的右子树。
中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。image.png实际上,二叉树的前、中、后序遍历就是一个递归的过程。比如,前序遍历,其实就是先打印根节点,然后再递归地打印左子树,最后递归地打印右子树。
二叉树时间复杂度:
从前面画的前、中、后序遍历的顺序图,可能看出来,每个节点最多会被访问两次,于是遍历操控的时间复杂度,跟节点的个数 n 成正比,也就是说二叉树遍历的时间复杂度是 O(n)。
二叉树还可以按层数遍历(广度优先)
第1层有1个元素, 最左边的是1
第2层有2个元素, 最左边的是2
4就是第3层有4个元素, 最左边的
8就是第4层有8个元素, 最左边的
第5层有16个元素,最左边的是16
第n层有2^(n-1)个元素,最左边的是 2^(n-1)image.png
二叉查找树
二叉查找树是二叉树中最常用的一种类型,也叫二叉搜索树。顾名思义,二叉查找树是为了实现快速查找而生的。不过,它不仅仅支持快捷查找一个数据,还拥护快速插入、删除一个信息。
这些都依赖于二叉查找树的特殊结构。二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。image.png
二叉查找树操作
第一,我们看如何在二叉查找树中查找一个节点。我们先取根节点,假如它等于我们要查找的数据,那就返回。假设要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。
image.png
二叉查找树插入操作
如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新信息直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的资料比节点数值小,并且节点的左子树为空,就将新材料插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
image.png
二叉查找树删除操控
二叉查找树的查找、插入操作都比较简单易懂,但是它的删除操作就比较复杂了 。针对要删除节点的子节点个数的不同,我们需要分三种情况来处理。
第一种情况要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。就是是,若比如图中的删除节点 55。
第二种情况是,假如要删除的节点只有一个子节点(只有左子节点或者右子节点),大家只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就允许了。比如图中的删除节点 13。
第三种情况最小节点了),所以,我们行应用上面两条规则来删除这个最小节点。就是是,如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。接着再删除掉这个最小节点,缘于最小节点肯定没有左子节点(要是有左子结点,那就不比如图中的删除节点 18。image.png
二叉查找树其他操作
除了插入、删除、查找处理之外,二叉查找树中还可以拥护快速地查找最大节点和最小节点、前驱节点和后继节点。
二叉查找树除了支持上面几个操作之外,还有一个要紧的特性,就是中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n),非常高效。因此,二叉查找树也叫作二叉排序树。
支持重复数据的二叉查找树
一个包含很多字段的对象。我们利用对象的某个字段作为键值(key)来构建二叉查找树。我们把对象中的其他字段叫作卫星数据。就是前面讲二叉查找树的时候,我们默认树中节点存储的都是数字。很多时候,在实际的软件开发中,我们在二叉查找树中存储的,
前面我们讲的二叉查找树的管理,针对的都是不存在键值相同的情况。那如果存储的两个对象键值相同,这种情况该怎么处理呢?我这里有两种解决方法。
第一种方法比较容易。二叉查找树中每一个节点不仅会存储一个数据,因此我们通过链表和支持动态扩容的数组等数据结构,把值相同的数据都存储在同一个节点上。
说,把这个新插入的数据当作大于这个节点的值来处理。就是第二种方法比较不好理解,不过更加优雅。每个节点仍然只存储一个数据。在查找插入位置的过程中,如果碰到一个节点的值,与要插入数据的值相同,我们就将这个要插入的数据放到这个节点的右子树,也就image.png当要查找数据的时候,遇到值相同的节点,我们并不停止查找管理,而是继续在右子树中查找,直到遇到叶子节点,才停止。这样就可以把键值等于要查找值的所有节点都找出来。
image.png
对于删除操作,大家也需要先查找到每个要删除的节点,然后再按前面讲的删除操作的方法,依次删除。image.png
Java中完成的数据结构
平台声明:文章内容(如有图片或视频亦包括在内)由作者上传并发布,文章内容仅代表作者本人观点,简书系信息发布平台,仅提供信息存储服务

喜欢的朋友记得点赞、收藏、关注哦!!!




















 浙公网安备 33010602011771号
浙公网安备 33010602011771号