文章目录


LeetCode 100，判断两棵二叉树是否相同【难度：简单；通过率：63.4%】，这道题是理解二叉树递归遍历的绝佳入门练习

一、 题目描述

给你两棵二叉树的根节点 p 和 q，请你写一个函数来检验它们是否相同

若是两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的

示例:

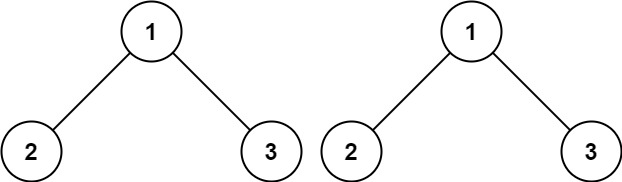
输入: p = [1,2,3], q = [1,2,3]
输出: true
解释: 两棵树结构相同，节点值也相同

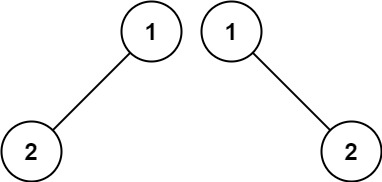
输入: p = [1,2], q = [1,null,2]
输出: false
解释: 两棵树结构不同

二、 核心思路：递归地比较

判断两棵树是否相同，我们可以从它们的根节点开始，一步步地进行比较。这自然引出了递归的思路：

  1. 比较根节点：起初，判断两棵树的根节点是否相同
  2. 递归比较左子树：然后，判断第一棵树的左子树和第二棵树的左子树是否相同
  3. 递归比较右子树：终于，判断第一棵树的右子树和第二棵树的右子树是否相同

只有当这三个条件（根节点相同，左子树相同，右子树相同）都满足时，大家才能说这两棵树是相同的

三、 递归的终止条件 (Base Cases)

在递归函数中，正确设置终止条件至关重要。对于判断两棵树是否相同，有以下几种情况需考虑：

  • 情况一：两个节点都为空
    • 如果 p 和 q 都指向 null（即都是空节点），那么它们当然是相同的。返回 true
  • 情况二：一个节点为空，另一个不为空
    • 如果 p 为 null 而 q 不为 null，或者 p 不为 null 而 q 为 null，那么它们显然是不同的。返回 false
  • 情况三：两个节点都不为空，但值不同
    • 如果 p 和 q 都不为 null，但 p.val != q.val，那么它们的值不同，树也不同。返回 false

四、 代码实现与解析

【一种参考代码】：

/**
* Definition for a binary tree node.
* public class TreeNode {
*     int val;
*     TreeNode left;
*     TreeNode right;
*     TreeNode() {}
*     TreeNode(int val) { this.val = val; }
*     TreeNode(int val, TreeNode left, TreeNode right) {
*         this.val = val;
*         this.left = left;
*         this.right = right;
*     }
* }
*/
class Solution {
// 主入口函数，直接调用辅助递归函数
public boolean isSameTree(TreeNode p, TreeNode q) {
return isSameNode(p, q);
}
/**
* 递归辅助函数，判断以 p 和 q 为根的两棵子树是否相同
* @param p 第一棵树的当前节点
* @param q 第二棵树的当前节点
* @return 如果两棵子树相同，则返回 true；否则返回 false
*/
public boolean isSameNode(TreeNode p, TreeNode q) {
// 1. 处理递归终止条件：当至少有一个节点为空时
// 这种写法合并了两种情况：
// (p == null && q == null) -> true (都为空，相同)
// (p == null && q != null) -> false (一个为空，一个不为空，不同)
// (p != null && q == null) -> false (一个为空，一个不为空，不同)
if (p == null || q == null) {
return p == null && q == null;
}
// 2. 如果两个节点都不为空，但它们的值不同，则直接返回 false
// 结构相同，但值不同，也不算相同
if (p.val != q.val) {
return false;
}
// 3. 如果当前节点值相同，则递归比较它们的左右子树
// 只有当左子树和右子树都完全相同，整个树才相同
boolean leftSame = isSameNode(p.left, q.left);
boolean rightSame = isSameNode(p.right, q.right);
return leftSame && rightSame;
// 也可以更简洁地写成：
// return isSameNode(p.left, q.left) && isSameNode(p.right, q.right);
}
}

五、 关键点与复杂度分析

  • 递归思维：将大问题（判断两棵树是否相同）分解为小问题（判断子树是否相同），直到达到最简单的基本情况（节点为空或值不同）
  • Base Case 的重要性编写正确递归函数的关键。将所有空节点和值不匹配的情况都考虑在内，并能正确终止递归就是：准确地定义递归的终止条件
  • 时间复杂度：O(N)其中 N 是两棵树中较小的那棵树的节点数。因为我们最多只需要遍历两棵树中较小的那棵树的所有节点。每个节点只会被访问一次，进行常数次比较处理
  • 空间复杂度：O(H)通过其中 H 是两棵树中较小的那棵树的高度。这主要是递归调用栈的空间开销。最坏情况下（树退化为链表），H 能够达到 N，所以空间复杂度为 O(N)

六、 总结与拓展

LeetCode 100 展示了如何借助递归将复杂的数据结构问题分解为更小、更易于管理的挑战；极其典型且易懂的递归思维

思路相似的题目：LeetCode101. 对称二叉树 - 力扣（LeetCode）

LeetCode 100 是判断两棵树是否“一模一样”否就是，那么 LeetCode 101 则是判断一棵树“左右对称”，核心思路与此题异曲同工，只是递归比较的子树方向有所调整

解析与两题对比参考：leetcode101.对称二叉树树（递归练习题）