P3901 数列找不同 查询莫队

解题思路

这是一个典型的离线查询问题，可以使用莫队算法高效解决。莫队算法的核心思想是通过对查询进行分块排序，然后利用滑动窗口的思想来处理查询，从而减少重复计算。

关键步骤：

分块处理：将查询按照左端点所在的块进行排序，同一块内的查询按右端点排序。

滑动窗口维护：使用双指针L和R维护当前区间，通过移动指针来调整区间范围。

 

统计元素出现次数：使用数组cnt记录当前区间内每个元素的出现次数，变量now记录当前区间内不同元素的数量。判断结果：对于每个查询，如果区间长度等于now，则说明区间内元素互不相同。

 

主体部分及输出：

预处理查询编号，用四个while移动指针顺便处理。

在这里着重说下四个while

 

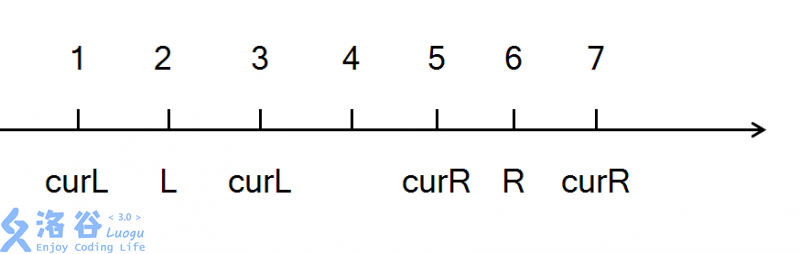
我们设想有一条数轴: 

当curL < L 时，我们当前curL是已经处理好的了。所以del时先去除当前curL再++

当curL > L 时，我们当前curL是已经处理好的了。所以 add 时先 -- 再加上改后的curL

当curR > R 时，我们当前curR是已经处理好的了。所以del时先去除当前curR再 --

当curR < R 时，我们当前curR是已经处理好的了。所以 add 时先++再加上改后的curR

代码注释

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;

// 定义查询结构体，存储每个查询的左右端点和查询编号
struct node{
    int l,r,id;
};

node t[N]; // 存储所有查询
int n,m,bcnt,L,R,a[N],cnt[N],now; // bcnt: 块大小; L,R: 当前区间左右指针; a: 原始数组; cnt: 计数数组; now: 当前区间内不同元素数量
int ans[N]; // 存储每个查询的结果

// 比较函数，用于对查询进行排序
bool cmp(node a,node b)
{
    // 如果左端点在同一块内，按右端点升序排序
    if(a.l / bcnt == b.l / bcnt) return a.r < b.r;
    // 否则按左端点升序排序
    else return a.l < b.l;
}

// 删除位置pos的元素
void del(int pos)
{
    cnt[a[pos]]--; // 减少该元素的计数
    if(cnt[a[pos]] == 0) now--; // 如果计数减到0，不同元素数量减1
}

// 添加位置pos的元素
void add(int pos)
{
    cnt[a[pos]]++; // 增加该元素的计数
    if(cnt[a[pos]] == 1) now++; // 如果计数从0增加到1，不同元素数量加1
}

int main()
{
    // 输入数据
    scanf("%d%d",&n,&m);
    bcnt = sqrt(n); // 计算块大小，通常取sqrt(n)
    for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
    
    // 输入查询
    for(int i = 1; i <= m; i++)
    {
        scanf("%d%d",&t[i].l,&t[i].r);
        t[i].id = i; // 记录查询编号
    }
    
    // 对查询进行排序
    sort(t + 1,t + 1 + m,cmp);
    
    // 初始化当前区间指针，可能也不用初始化？（雾）
    L = 1;
    R = 0;
    
    // 处理每个查询
    for(int i = 1; i <= m; i++)
    {
        int tl = t[i].l,tr = t[i].r;
        
        // 调整左指针L
        while(L < tl) del(L++); // 左指针右移，删除左边元素
        while(L > tl) add(--L); // 左指针左移，添加左边元素
        
        // 调整右指针R
        while(R < tr) add(++R); // 右指针右移，添加右边元素
        while(R > tr) del(R--); // 右指针左移，删除右边元素
        
        // 判断当前区间内元素是否互不相同
        if(tr - tl + 1 == now)
            ans[t[i].id] = 1; // 区间长度等于不同元素数量，说明互不相同
    }
    
    // 输出结果
    for(int i = 1; i <= m; i++)
        if(ans[i]) puts("Yes");
        else puts("No");
        
    return 0;
}