MCOI-2503月赛L3/L4选择题 解析
MCOI-2503月赛L3/L4选择题
一、单选题(5题,每题4分,共20分)
1、 在求最长上升子序列中,初始化动态规划数组f[i]为?
A. 1
B. 0
C. inf
D. -inf
解析:A.每个数字可以以自己为结尾,长度为1的上升子序列
2、 在求最长上升子序列中,设有序列数组a[]和动态规划数组f[],双重循环中外层循环i从1到n,内嵌套j从1到i-1,请问以下哪个条件满足上升趋势,以及状态转移方程?
A. if(a[i] > a[i - 1]) f[i] = max(f[i],f[i - 1] + 1);
B. if(a[i] > a[j]) f[i] = max(f[i],f[j] + 1);
C. if(a[i] > a[j]) f[j] = max(f[j],f[j] + 1);
D. if(a[i] < a[i - 1]) f[i] = max(f[i],f[i - 1] + 1);
解析:B. 读题可以知道i在右边,j在左边,上升趋势必然是右边大于左边,ai > aj;而构成的子序列应该是由fj+1得到fi的新长度做比较,所以是f[i] = max(f[i],f[j] + 1);
3、 在二维数组中,可向右、向下移动的情况下,从左上角(1,1)走到右下角(n,m)可有的方案数,以下描述正确的是:
A. 初始化f[1][1]为1,状态转移为f[i][j] = f[i][j + 1] + f[i + 1][j]
B. 初始化f[1][1]为0,状态转移为f[i][j] = f[i][j - 1] + f[i - 1][j]
C. 初始化f[1][1]为1,状态转移为f[i][j] = f[i][j - 1] + f[i - 1][j]
D. 初始化f[1][1]为0,状态转移为f[i][j] = f[i][j + 1] + f[i + 1][j]
解析:C. 二维移动dp,f[i][j]的意思是到达i行j列的方案数,则起点到达起点的方案数为1,所以f[1][1]为1,因为可以向右、下移动,则想要到达(i,j),必然从左边或者上边走过来,所以是f[i][j] = f[i][j - 1] + f[i - 1][j]
4、 关于背包问题,以下描述正确的是:
A. 01背包的特征是物品只能拿一次,状态转移可以为:f[容量j] = max(f[j],f[j - 重量w[i]] + 价值v[i]),其中j的循环是从w[i]到最大容量m正序循环;
B. 完全背包的特征是物品只能拿一次,状态转移可以为:f[容量j] = max(f[j],f[j - 重量w[i]] + 价值v[i]),其中j的循环是从w[i]到最大容量m正序循环;
C. 完全背包的特征是物品能拿不限次数,状态转移可以为:f[容量j] = max(f[j],f[j - 重量w[i]] + 价值v[i]),其中j的循环是从最大容量m到w[i]逆序循环;
D. 01背包的特征是物品只能拿一次,状态转移可以为:f[容量j] = max(f[j],f[j - 重量w[i]] + 价值v[i]),其中j的循环是从最大容量m到w[i]逆序循环;
解析:D.
01背包的特点是每个物品只能选一次,因此状态转移时,j必须逆序循环(从m到w[i]),避免重复计算。
完全背包的特点是物品可以选无限次,因此j必须正序循环(从w[i]到m),允许重复计算。
5、 以下图从节点1开始分别进行DFS、BFS,请分别列举出从小到大的DFS、BFS的编号顺序

A. 123654,125346
B. 125346,123654
C. 123456,125346
D. 123654,123456
解析:答案:A
● DFS(深度优先搜索):优先深入遍历,顺序如 1→2→3→6→5→4(123654)。
● BFS(广度优先搜索):按层次遍历,顺序如 1→2→5→3→4→6(125346)。
二、 程序阅读题(10题,每题4分,共40分)
题目(5倍经验):现在有 n 个好友,m个药剂,你将与好友们pk,有些朋友打败TA需要一定的药剂。给定失败时可获得的经验、胜利时可获得的经验,打败他至少需要的药量。
要求求出最大经验 s,输出 5s。
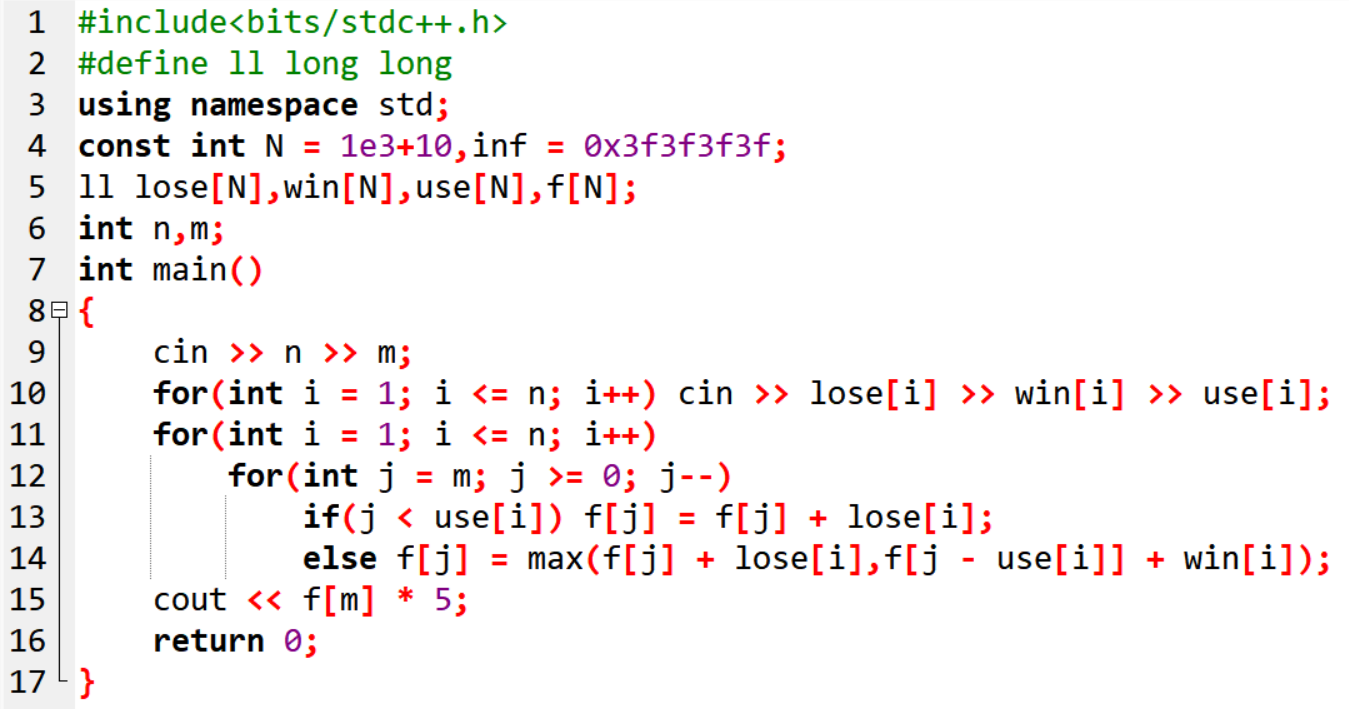
6、 该程序的时间复杂度为:
A. O(n)
B. O(n2)
C. O(m2)
D. O(n * m)
解析:答案:D
● 题目是01背包变种,外层循环n个好友,内层循环m个药剂容量,因此时间复杂度为 O(n * m)。
7、 在程序中,f[j]更契合的状态意思为:
A. 使用j个药时的最大经验
B. 使用j个药时的最小经验
C. 使用j个药时的平均经验
D. 使用j个药时的失败次数
解析:答案:A
● f[j] 是背包DP的经典定义,表示使用j个药时的最大经验值。
8、 当输入数据为以下的数据时,输出结果应为:
|
6 8 21 52 1 21 70 5 21 48 2 14 38 3 14 36 1 14 36 2 |
A. 212
B. 1060
C. 4080
D. 5300
解析:答案:B
● 题目要求输出 5倍经验,计算后应为 1060(即 212 * 5)。
9、 根据01背包的一维模板,第12行修改为for(int j = m; j >= use[i]; j--)也是可以得到正确结果
A. 正确
B. 错误
解析:答案:B
● 本题 < use[i]时意为失败,根据题意失败也会获得经验,所以不可以只>=use[i]
10、 若将f数组扩展到二维,f[i][j]描述为:挑战前i个好友且只使用j个药剂时的最大经验,则以下哪个状态转移是挑战胜利时的状态转移方程:
A. f[i][j]=max(f[i-1][j-use[i]]+win[i],f[i-1][j-1]+lose[i])
B. f[i][j]=max(f[i][j-use[i]]+win[i],f[i][j]+lose[i])
C. f[i][j]=max(f[i-1][j-use[i]]+win[i],f[i-1][j])
D. f[i][j]=max(f[i-1][j-use[i]]+win[i],f[i-1][j]+lose[i])
解析:答案:D
● 胜利时,消耗 use[i] 药,获得 win[i] 经验,因此状态转移为 f[i-1][j-use[i]] + win[i]。
● 失败时,不消耗药,获得 lose[i] 经验,因此状态转移为 f[i-1][j] + lose[i]。
题目(图的存储):阅读以下邻接表的存储程序,回答问题
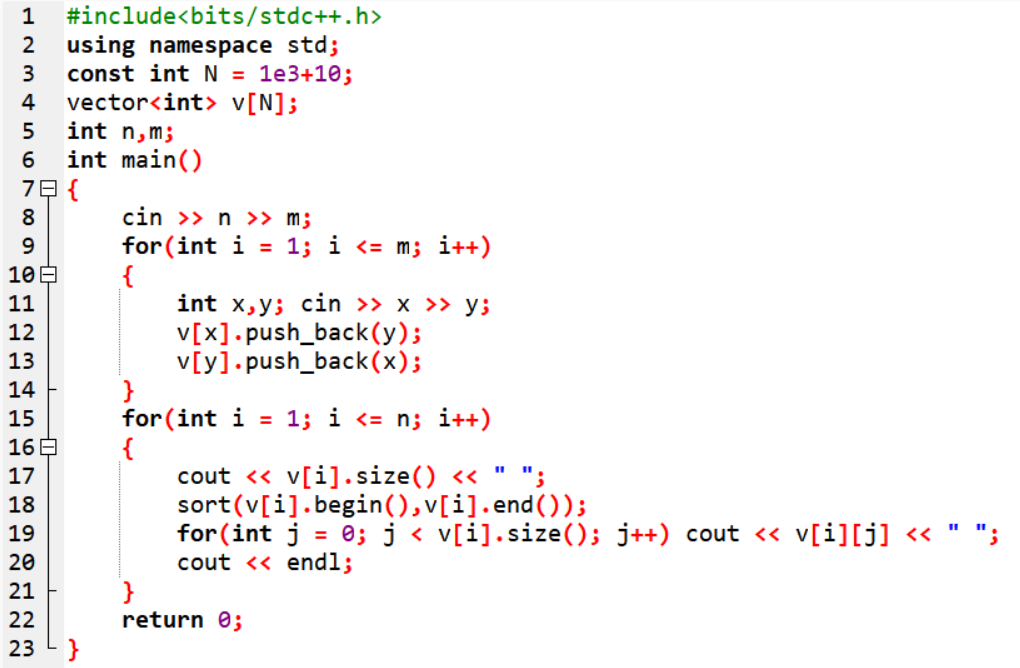
11、 在程序中,v[x].push_back(y)的作用是什么?
A. 将节点 y从节点 x 的邻接表中移除
B. 将节点 y 添加到节点 x 的邻接表中
C. 将节点 x 添加到节点 y 的邻接表中
D. 将节点 x 和节点 y 的邻接表合并
解析:
● v[x].push_back(y) 表示将节点 y 添加到节点 x 的邻接表,即建立 x→y 的边。
● 由于程序中还有 v[y].push_back(x),说明这是一个无向图(双向存储)。
答案:B
12、 程序中使用了sort(v[i].begin(), v[i].end()),其目的是?
A. 对节点 i 的邻接表进行降序排序
B. 对节点 i 的邻接表进行升序排序
C. 删除节点 i 的邻接表中的重复元素
D. 计算节点 i 的邻接表的大小
解析:
● sort(v[i].begin(), v[i].end()) 默认按升序排序(从小到大)。
● 目的是让邻接表的节点编号有序,方便后续处理(如 BFS/DFS 遍历)。
答案:B
13、 在程序中,v[i].size()表示什么?
A. 节点 i 的度数 B. 节点 i 的权重
C. 节点 i 的编号 D. 节点 i 的深度
解析:
● v[i].size() 表示节点 i 的邻接表大小,即与节点 i 直接相连的边数,也就是度数。
答案:A
14、 如果输入的图是一个完全图,程序输出的每个节点的度数是多少?
A. n - 1
B. n
C. m
D. m - 1
解析:
● 完全图中,每个节点与其他所有节点相连,因此度数为 n - 1(n 是总节点数)。
● 例如,3 个节点的完全图,每个节点的度数为 2。
答案:A
15、 在程序中,v[y].push_back(x)的作用是什么?
A. 确保图是有向图
B. 确保图是无向图
C. 确保图是连通图
D. 确保图是完全图
解析:
● 程序中同时存在 v[x].push_back(y) 和 v[y].push_back(x),表示双向存储边,因此是无向图。
● 如果只有 v[x].push_back(y),则是有向图。
答案:B
三、 程序填空题(10题,每题4分,共40分)
题目(登山):一座山有n个排成一排的景点高度,第i个景点的高度为a[i],现在登山队的成员会从左往右选择任意一个景点开始浏览,成员们会依次经历上山和下山两个阶段,上山时,成员们浏览的下一个景点高度必须比当前景点高度高(即a[i+1] > a[i]);下山时,成员们浏览的下一个景点高度必须比当前景点高度低(即a[i+1]<a[i]),请你计算成员们依次经历上山和下山后,最多可以浏览的景点个数

16、 在程序中,f[i] 和 g[i] 的初始值应该是什么?(空①)
A. 0
B. 1
C. a[i]
D. n
解析:
● f[i] 表示以 a[i] 结尾的最长上升子序列长度,初始时每个景点自身构成长度为 1 的序列。
● g[i] 同理,表示以 a[i] 结尾的最长下降子序列长度,初始值也应为 1。
答案:B
17、 在计算 f[i] 时,内层循环的条件应该是什么?(空②)
A. for(int j = 1; j < i; j++)
B. for(int j = i + 1; j <= n; j++)
C. for(int j = 1; j <= n; j++)
D. for(int j = i; j >= 1; j--)
解析:
● f[i] 是以 a[i] 结尾的最长上升子序列,需要检查 a[i] 之前的所有 a[j](即 j < i)。
● 因此,内层循环应为 for(int j = 1; j < i; j++)。
答案:A
18、 在计算 g[i] 时,条件判断应该是什么?(空③)
A. a[i] == a[j]
B. a[i] < a[j]
C. a[i] > a[j]
D. a[i] <= a[j]
解析:
● g[i] 是以 a[i] 结尾的最长下降子序列,需要满足 a[i] < a[j](即当前景点高度比后续景点低)。
● 但题目描述中,下山阶段要求 a[i+1] < a[i],因此 g[i] 的条件应为 a[i] > a[j](逆序检查)。
答案:C
19、 在计算最终答案时,ans 的更新条件应该是什么?(空④)
A. f[i] + g[i]
B. f[i] + g[i] - 1
C. f[i] - g[i]
D. f[i] * g[i]
解析:
● 题目要求上山 + 下山的最长路径,即 f[i](上升)和 g[i](下降)的总和。
● 但 a[i] 被重复计算了一次(既是上升的终点,也是下降的起点),因此需要减 1。
答案:B
20、 程序的最终输出应该是什么?(空⑤)
A. ans
B. ans + 1
C. ans - 1
D. ans * 2
解析:
● 根据题目逻辑,ans 已经是 f[i] + g[i] - 1 的最大值,直接输出即可。
答案:A
题目(图的遍历):给定n个点m条有向边<x,y>,点的编号从1到n,根据编号从小到大输出该图的广度优先搜索BFS的遍历编号
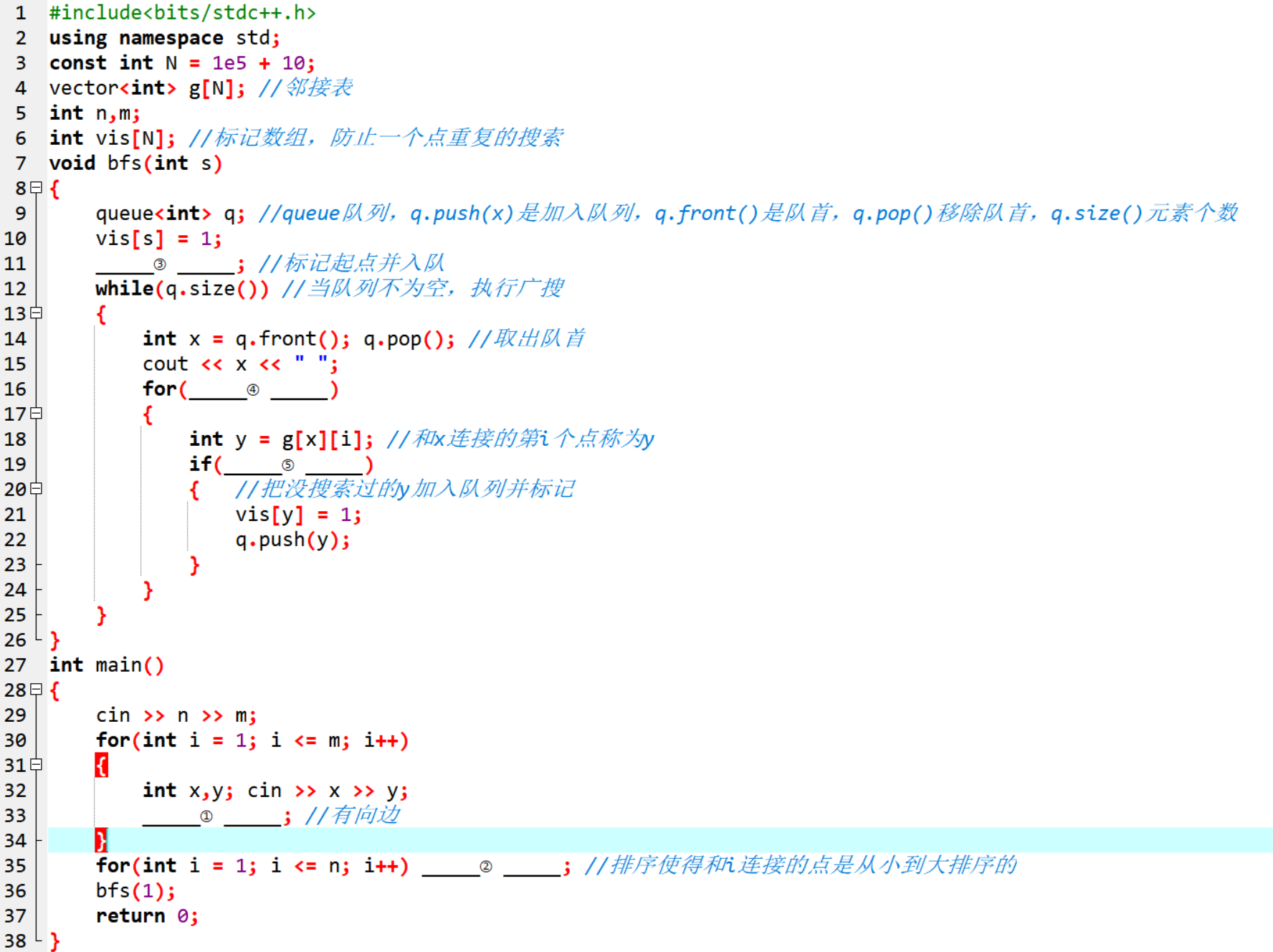
21、 在程序中,如何表示有向边的连接关系?(空①)
A. g[x].push_back(y);
B. g[y].push_back(x);
C. g[x].push_back(y); g[y].push_back(x);
D. g[y].push_back(x); g[x].push_back(y);
解析:
● 有向图只需单向存储边,即 x→y,因此只需 g[x].push_back(y)。
● 若为无向图,则需要双向存储(选项C/D)。
答案:A
22、 在程序中,如何对每个节点的邻接表进行排序?(空②)
A. sort(g[i].begin(), g[i].end());
B. sort(g[i].rbegin(), g[i].rend());
C. reverse(g[i].begin(), g[i].end());
D. g[i].sort();
解析:
● 题目要求按编号从小到大遍历邻接点,需用 sort(g[i].begin(), g[i].end()) 升序排序。
● 选项B是降序,C是逆序(不保证有序),D语法错误。
答案:A
23、 在BFS函数中,如何标记起点后将其入队?(空③)
A. q.push(s);
B. q.pop(s);
C. q.front(s);
D. q.size(s);
解析:
● BFS的起点 s 需先标记(vis[s]=1),再通过 q.push(s) 加入队列。
● 其他选项:pop 是移除队首,front 是访问队首,size 是查询大小,均不符合。
答案:A
24、 在BFS函数中,如何遍历与节点 x 相连的所有节点?(空④)
A. for(int i = 1; i < g[x].size(); i++)
B. for(int i = 1; i <= g[x].size(); i++)
C. for(int i = 0; i <= g[x].size(); i++)
D. for(int i = 0; i < g[x].size(); i++)
解析:
● C++中向量索引从 0 开始,因此循环应为 for(int i = 0; i < g[x].size(); i++)。
● 选项A/B的起始索引错误,选项C会越界。
答案:D
25、 在BFS函数中,如何判断节点 y是否未被访问过?(空⑤)
A. if(vis[y] > 0)
B. if(vis[y] == 1)
C. if(vis[y] != 0)
D. if(vis[y] == 0)
解析:
● vis[y] == 0 表示未访问,vis[y] == 1 表示已访问。
● 题目要求判断未被访问,因此条件是 vis[y] == 0。
答案:D




 浙公网安备 33010602011771号
浙公网安备 33010602011771号