一、实验结论:
1.实验任务5:
vectorint.hpp:
#include <iostream> #include <iomanip> using namespace std; class vectorint { public: vectorint(int n) : size{n} { cout << "constructor 1 called." << endl; p = new int[size]; } vectorint(int n, int value) : size{n} { cout << "constructor 2 called." << endl; p = new int[size]; int i; for (i = 0; i < size; i++) p[i] = value; } ~vectorint() { cout << "destructor called." << endl; delete[] p; } int &at(int index) { if (index >= 0 && index < size) return p[index]; } vectorint(const vectorint &v1) : size{v1.size} { cout << "copy constructor called." << endl; p = new int[size]; int i; for (i = 0; i < size; i++) p[i] = v1.p[i]; } int get_size() const { return size; } friend int output(vectorint &v) { int i; for (i = 0; i < v.size; i++) cout << v.p[i] << " "; cout << endl; } private: int size; int *p; };
task5.cpp:
#include <iostream> #include "vectorint.hpp" void test() { using namespace std; int n; cin >> n; vectorint x1(n); for(auto i = 0; i < n; ++i) x1.at(i) = i*i; output(x1); vectorint x2(n, 42); vectorint x3(x2); output(x2); output(x3); x2.at(0) = 77; output(x2); output(x3); } int main() { test(); }
运行结果:
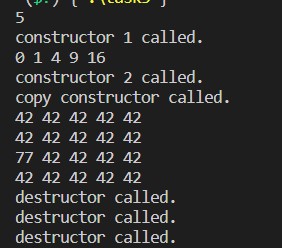
2.实验任务6:
Matrix.hpp:
#pragma once #include <iostream> using namespace std; class Matrix { public: Matrix(int n) : lines{n}, cols{n} { p = new double*[lines]; int i; for (i = 0; i < lines;i++) p[i] = new double[cols]; } // 构造函数,构造一个n*n的矩阵 Matrix(int n, int m) : lines{n}, cols{m} { p = new double *[lines]; int i; for (i = 0; i < lines; i++) p[i] = new double[cols]; } // 构造函数,构造一个n*m的矩阵 Matrix(const Matrix &X) { lines = X.lines; cols = X.cols; p = new double *[lines]; int i,j; for (i = 0; i < lines; i++) p[i] = new double[cols]; for (i = 0; i < lines; i++) for (j = 0; j < cols; j++) p[i][j] = X.p[i][j]; } // 复制构造函数,使用已有的矩阵X构造 ~Matrix() { delete[] p; } // 析构函数 void set(const double *pvalue) { int i, j; for (i = 0; i < lines; i++) for (j = 0; j < cols; j++) p[i][j] = *(pvalue + i * cols + j); } // 用pvalue指向的连续内存块数据按行为矩阵赋值 void set(int i, int j, int value) { p[i][j] = value; } // 设置矩阵第i行第j列元素值为value double &at(int i, int j) { return p[i][j]; } // 返回矩阵第i行第j列元素的引用 double at(int i, int j) const { return p[i][j]; } // 返回矩阵第i行第j列元素的值 int get_lines() const { return lines; } // 返回矩阵行数 int get_cols() const { return cols; } // 返回矩列数 void print() const { int i, j; for (i = 0; i < lines; i++) { for (j = 0; j < cols; j++) cout << p[i][j] << " "; cout << endl; } cout << endl; } // 按行打印输出矩阵 private: int lines; // 矩阵行数 int cols; // 矩阵列数 double **p; // 指向存放矩阵数据的内存块的首地址 };
task6.cpp(数据1):
#include <iostream> #include "Matrix2.hpp" void test() { using namespace std; double x[] = {1, 2, 3, 4, 5, 6}; Matrix m1(3, 2); // 创建一个3×2的矩阵 m1.set(x); // 用一维数组x的值按行为矩阵m1赋值 m1.print(); // 打印矩阵m1的值 cout << "the first line is: " << endl; cout << m1.at(0, 0) << " " << m1.at(0, 1) << endl; // 输出矩阵m1第1行两个元素的值 cout << endl; Matrix m2(2, 3); m2.set(x); m2.print(); cout << "the first line is: " << endl; cout << m2.at(0, 0) << " " << m2.at(0, 1) << " " << m2.at(0, 2) << endl; cout << endl; Matrix m3(m2); // 用矩阵m2构造新的矩阵m3 m3.set(0, 0, 999); // 将矩阵m3第0行第0列元素值设为999 m3.print(); } int main() { test(); }
数据1运行结果:
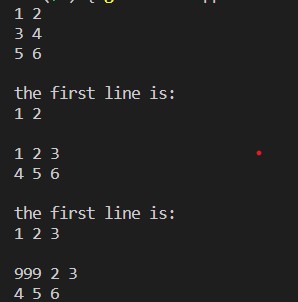
task6.cpp(数据2,只展示改动部分代码):
double x[] = {1, 2, 3, 4, 5, 6,7,8,9,10,11,12}; Matrix m1(4, 3); // 创建一个4×3的矩阵 m1.set(x); // 用一维数组x的值按行为矩阵m1赋值 m1.print(); // 打印矩阵m1的值 cout << "the first line is: " << endl; for (int i = 0; i < 3;i++) cout << m1.at(0, i) << " " ; // 输出矩阵m1第1行3个元素的值 cout << endl; Matrix m2(2, 6); m2.set(x); m2.print(); cout << "the first line is: " << endl; for(int i = 0; i < 6; i++) cout<< m2.at(0, i) << " "; cout << endl;
数据2运行结果:
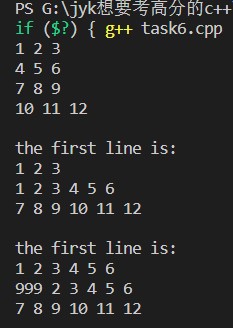
二、实验总结:
1.在此次实验中书写类的过程中,部分之前学过的内容如友元函数已经忘记,需要及时复习。
2.在实验任务6中,我将private接口中p的声明改成了double **p,目的是让p指向一个存储元素为指向一维数组指针的一维数组,这样便将二维数组转化成了一维数组求解。(啊这样写应该是可以的吧(小声)(擦汗))


