【ACWING】数论2

1 欧拉函数

f(n)：表示1-n中与n互质的数的个数

1.1 欧拉定理

定理 设m是任意大于1的整数，gcd(a,m)=1,即a、m互质,则

          a^φ(m)≡1（mod m）----->同余定理

1. 当m=质数的时候，φ(m)=m-1，从而引出费马定理：a^m-1 ≡1（mod m）

2 快速幂

快速求出来（Ologk）a^k % p的结果，1 <= a,p,k <= 1e9

预处理过程： 前一个的结果的平方，再mod p

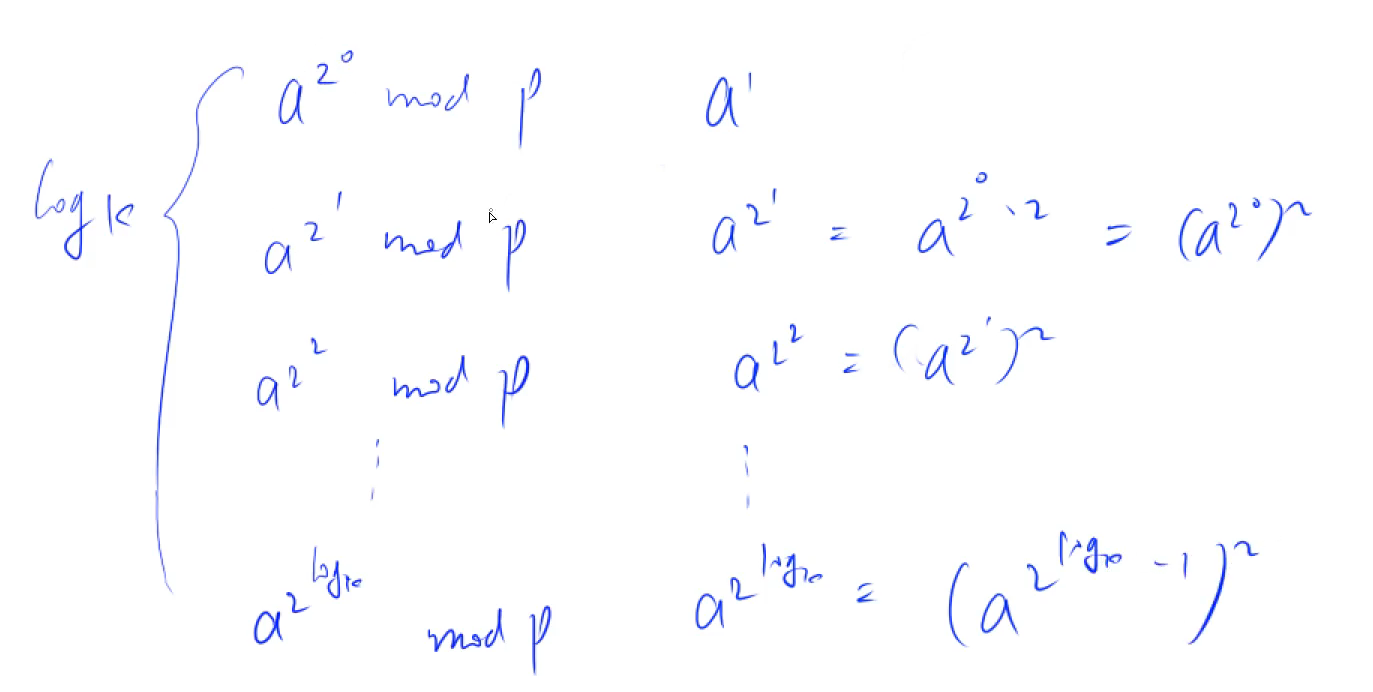
LL qmi(int a, int k, int p)
{
	LL res = 1;
    while(k)
    {
        if(k&1) res = (LL) res * a % p;		// 如果末位为1
        k>>1;
        a = (LL)a*a %p;	// a的平方
    }
    return res;
}

3 裴蜀定理/贝祖定理

对任何整数a,b，关于未知数x和y的线性丢番图方程(称为裴蜀等式):ax+by=c，方程有整数解当且仅当c是gcd(a,b)的倍数。裴蜀等式有解时必然有无穷多个解。解的形式如下

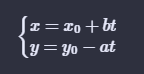
由上面的描述可知：已知某个最大公约数d = gcd(a,b), 则必然存在一组整数（可以为负数）x，y满足ax + by = d

1. 换一种说法，对于任意正整数a,b，一定存在整数x,y，使得ax+by=gcd(a,b)
2. 也就是说，用a,b的组合去凑一个新的数出来。并且gcd(a,b)是他们凑出来的最小正整数

证明就很简单了，a和b是gcd(a,b)的倍数，那么显然a,b的组合也会是gcd(a,b)的倍数

4 拓展欧几里得定理

该方法是用来求解gcd的，但是！ 他能够在求gcd的过程中，给出上面裴蜀定理的一组解

建议直接看这个题解

我们来分情况讨论一下扩展欧几里得定理：

即当我们用扩展欧几里得定理求x和y时，欧几里得定理每递归一次x不用变,y->y-a/b * x即可
如果我们求出x和y的一对，我们记为x0和y0
那么其他的x和y可以通过x0，y0表示:
令a’=a/gcd(a,b) , b’=b/gcd(a,b);

那么其他的x和y可以表示为：x=x0+kb’,y=y0-ka’;

这个通解 = 特解 + 齐次解，这里齐次解由 解ax+by=0得到的，反正带进去=0就对了

求得一组解之后，能够很容易构造出通解的形式，如下图

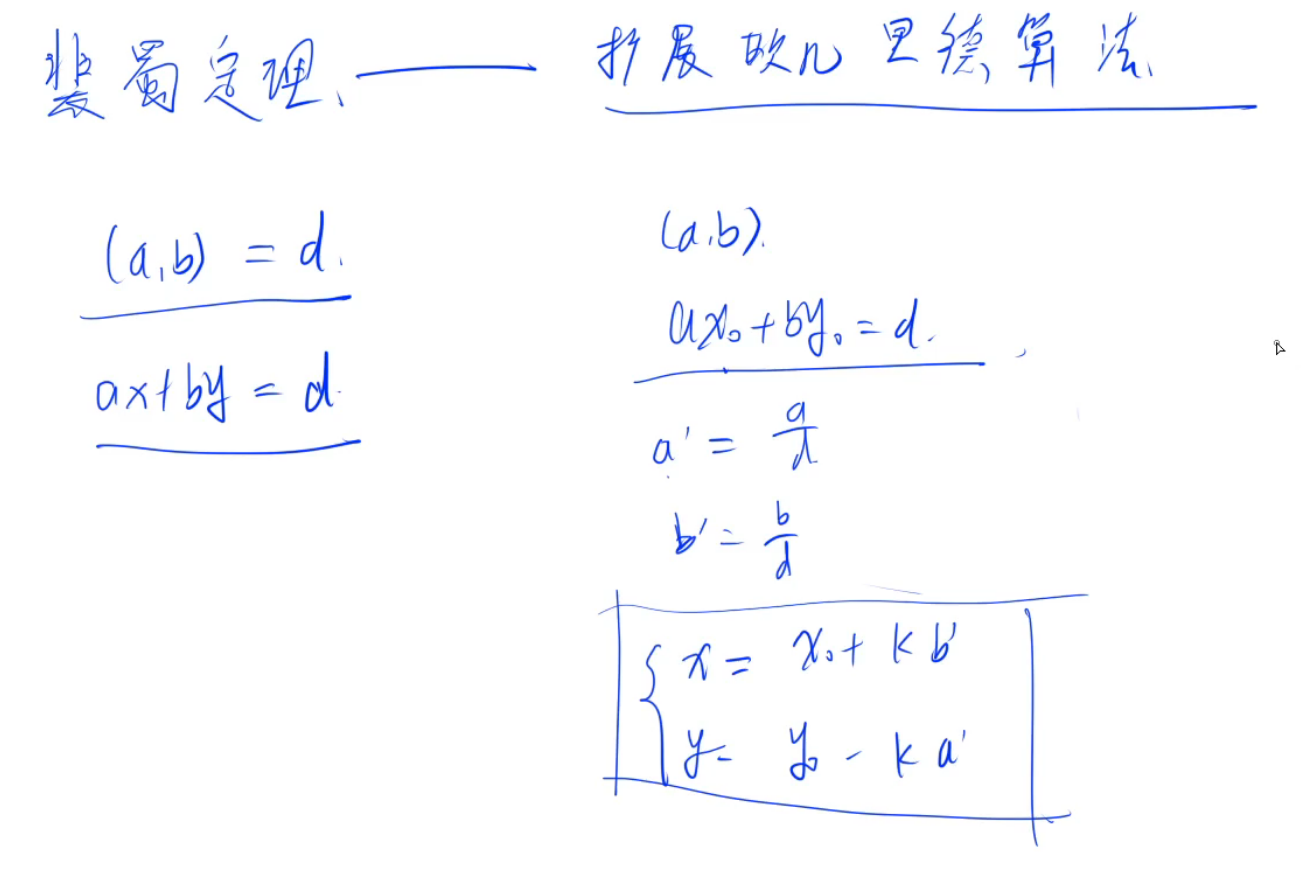
int exgcd(int a, int b, int &x, int &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);    //辗转相除
    y -= a/b * x;
    return d;
}

5 中国剩余定理

求 a的逆 相当于解ax=1(mod m), 用扩展欧几里得就行