【ACWING】数论1

1 质数

1.1 质数的判定 -- 试除法O(n)

bool is_prime(int n)
{
	if(n < 2) return false;
    //for(int i = 2; i < n; i++)	// 这个最简单，但是复杂度高
	for(int i = 2; i <= n / i; i ++) 	// 实际上只枚举了sqrt(n)次
    	if(n%i == 0) return false;
    
    return true;
}

在上述优化中，推荐写成i<=n/i，不推荐i * i < n，因为i*i会爆int，也不推荐sqrt(n)，因为每次循环都会算一次

1.2 分解质因数----试除法

首先由算术基本定理可知，任何整数都能分解成若干个质因子的乘积。

void divide(int n)
{
	for(int i = 2; i <= n; i++)		// 从2开始枚举，2是第一个质数 
        if(n%i ==0)	   //发现能整除 i 
        {
            int s = 0;		// 统计除了几次i 
            while(n%i==0)	// 只要还能除i，就继续除 
            {
                n/=i;
                s++;
            }
            printf("%d %d\n",i,s);
        }
}
 
// 下面这个写法好像更好
void divide(int n)
{
    unordered_map<int,int> primes;
    for(int i = 2; i <= n/i; i++){
		while(n%i==0)
        {
            n/=i;
            primes[i]++;
        }
    }
    if(n>1) primes[n]++;    // 剩余一个大于n/i的质因子
}

优化1---O(sqrt(n))

n中最多只包含一个大于sqrt(n)的质数

void divide(int n)
{
	for(int i = 2; i <= n / i; i++)		// 只枚举到sqrt(n) 
	if(n%i ==0)	   //发现能整除 i 
	{
		int s = 0;		// 统计除了几次i 
		while(n%i==0)	// 只要还能除i，就继续除 
		{
			n/=i;
			s++;
		}
		printf("%d %d\n",i,s);
	}
    
    if(n>1) printf("%d %d\n",n,1);	// 最后仅剩的大于sqrt(n)的质因子
}

1.3 质数筛

最朴素版本

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)		// 从2开始判断
    {
        if(!st[i]) {
           primes[cnt++] = i;	// 如果i这个数没有被筛掉，说明i是质数，primes存的是质数表
        }
        for(int j = i + i; j <= n; j += i) st[j] = true;
    }
}

埃式筛

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)		// 从2开始判断
    {
        if(!st[i]) {
           	primes[cnt++] = i;	// 如果i这个数没有被筛掉，说明i是质数，primes存的是质数表
        	for(int j = i + i; j <= n; j += i) st[j] = true;	// 把这个放进循环里面了，相当于只筛质数
        }
    }
}

欧拉筛

void get_primes(int n)
{
	for(int i = 2; i <= n; i++)          // 对2-n这些数一个个处理
    {
        if(!st[i]) primes[cnt++] = i;    // st[] = false，表示这个数没有被筛掉
        for(int j = 0; primes[j] <= n/i; j++)      // 用[质数*i]得到的数一定不是质数，筛掉（保证这个数<n）
        {
            st[primes[j] * i] = true;          // 
            if(i % primes[j] == 0) break;
        }
    }
}

2 约数

2.1 试除法求约数

因为约数是成对出现的，假设n能被d整除，那么n同样能够被n/d整除，所以枚举的时候有d<=n/d，所以d<=sqrt(n)

vector<int> get_divisors(int n)
{
	vector<int> res;
    for(int i = 1; i <= n/i; i ++)
    {
        if(n%i==0)		// 能整除，说明i是n的约数
        {
            // 约数成对出现，加入数组
         	res.push_back(i);
            if(i!= n/i) res.push_back(n/i);
        }
    }
    sort(res.begin(),res.end());
    return res;
}

2.2 约数个数 约数之和

由算术基本定理来推

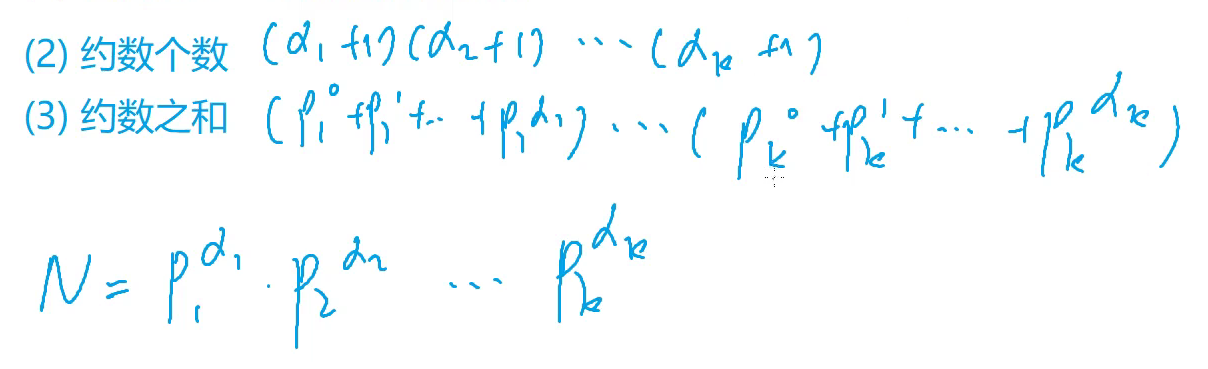
2.3 欧几里得算法/辗转相除法法

原理：gcd(a,b) = gcd(b,a%b) 辗转相除

int gcd(int a, int b)
{
    return b ? gcd(b,a % b) : a;
}

同时可知，最小公倍数lcm = a*b / gcd(a,b)