搜索与图论3

0 前言

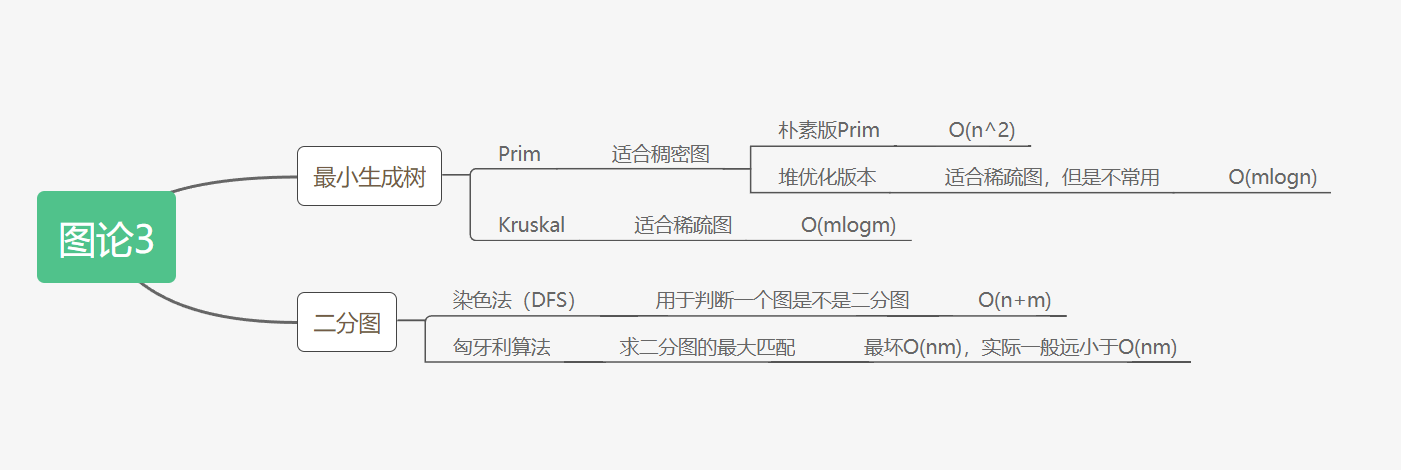
1 最小生成树算法

1.1 Prim算法

算法思路：

1. 初始化距离为正无穷
2. n次迭代，每次选一个点进入到生成树集合中
 	1. 找到集合外距离最近的点`t`
 	2. 用`t`更新其他点到集合的距离（集合就是指当前生成的连通图/生成树）
 	3. `st[t] = true`，表示将`t`加入集合中

int prim()
{
	memset(dist,0x3f,sizeof dist);	// 距离全部初始化为＋∞
   
    int res = 0;		// 存最小生成树所有边权之和
    
    for(int i = 0; i< n; i++)	// n次迭代，每次能选中一个点
    {
        // 找打距离最小生成树集合的最小的点
        int t = -1;
        for(int j = 1; j<=n; j++)
       		if(!st[j] && (t==-1 || dist[t] > dist[j]))		// 点j不在集合中，且距离更小 
                t = j;
        
        // 如果不是第一个点，且距离INF，则无法生成最小生成树
        if(i && dist[t] == INF) return INF;
        if(i) res += dist[t];		
        
        // 用t的值更新其他点的值。注意和g[t][j]比就好了。
        // 因为dist存的是到集合的距离，那么每个点到这个集合的距离，实际上就是这个集合的出边的边长
        for(int j = 1; j<=n; j++) dist[j] = min(dist[j],g[t][j]);
        
        st[t] = true;	// 表示将该点加入生成树集合中了
    }
    return res;
}

1.2 Kruskal算法

1. 将所有边按权重从小到大排序-------------算法的瓶颈（O(mlogm)）
2. 枚举每条边，如果这条边能使得图连通，就将这条边加入到集合中

Kruskal只需要对边处理，所以可以像bellman-ford一样，用结构体存边就好了。

---

2 二分图

二分图就是，我可以将图中的点分割为两个互不相交的子集（点可以不平均分割），边的话只存在两个子集之间，子集内部没有边

2.1 染色法-判断二分图

一个图是二分图，当且仅当图中不含奇数环

2.2 匈牙利算法--求二分图最大匹配