【ACWING】前缀和、差分

前缀和

直接看模板题就好啦

前缀和

设有一个数列{a1,a2,a3...an},前缀和Sn=a1+a2+a3+...+an，就是数列的前n项和，其中，要求其下标从1开始，规定S0=0

1. 如何求前缀和 ：递归==> S[n]=S[n-1]+a[i]
2. 前缀和有什么用：求一段数组的和，比如求[l,r]数列之和，即S[r]-S[l-1]

//数列初始化
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
//前N项和初始化
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];

//区间和公式
int l,r;
cout<<s[r]-s[l-1]<<endl;

二维前缀和

求子矩阵的和

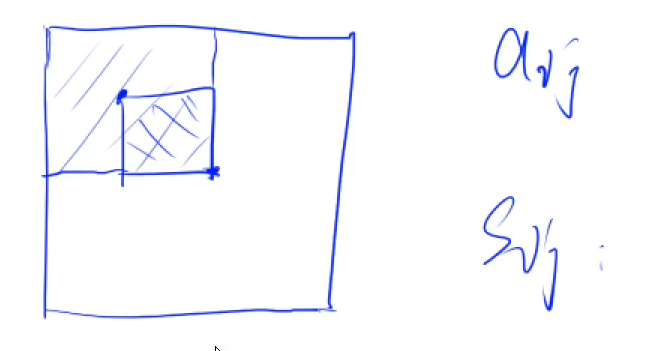
求(X1,Y1)到(X2,Y2)的大小

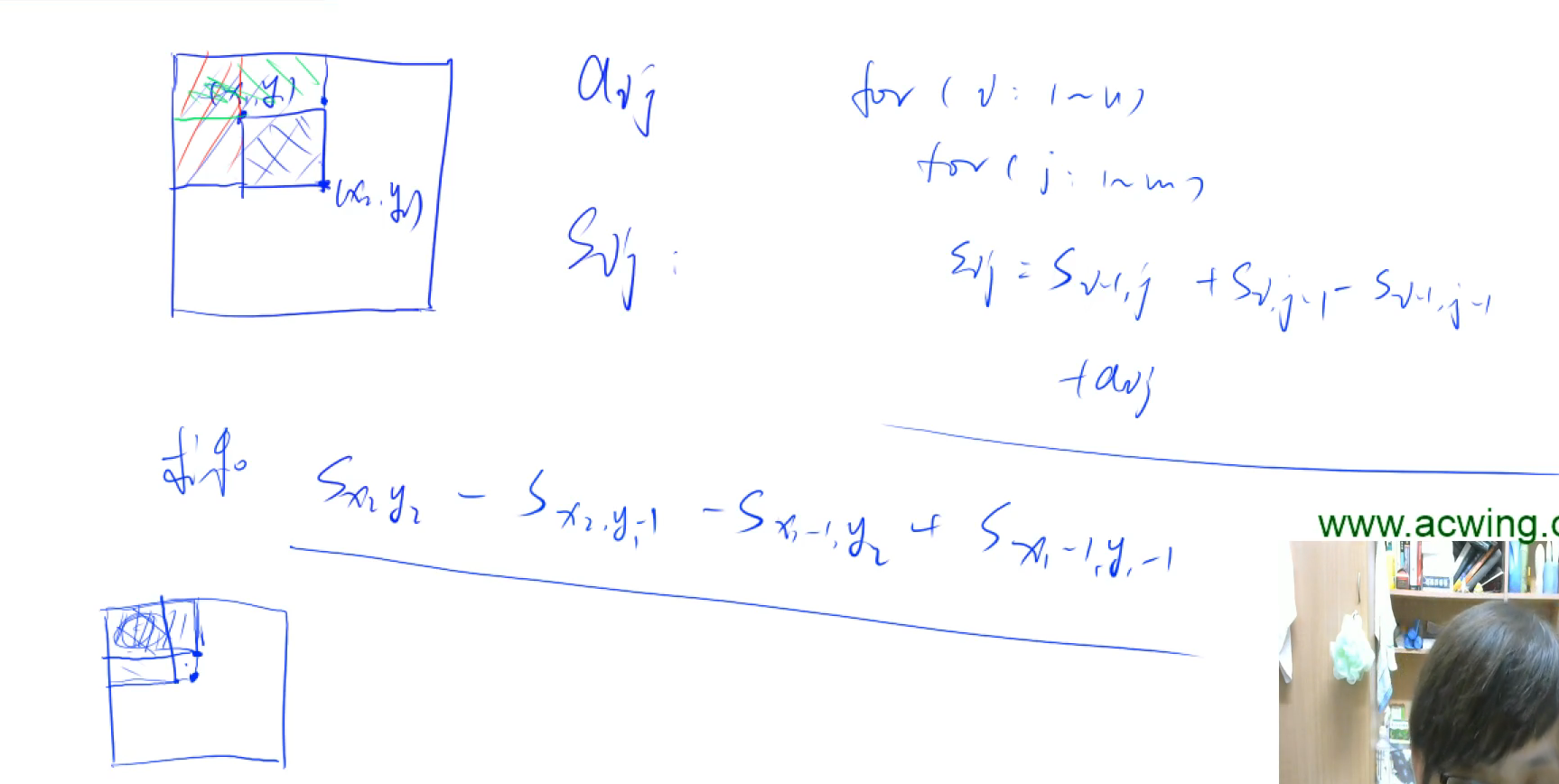
//二位矩阵的初始化，以及二维前缀和
for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
        scanf("%d",&a[i][j]);

for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
        s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];

//计算子矩阵
int x1,x2,y1,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d/n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);

注意事项

1. 注意，这两种前缀和，我们习惯性下标从1开始

2. 关于全局数据的初始化和局部数组的初始化问题：对于全局数组，编译器默认初始化内容为0；对于局部数组（比如在main函数里的数组），默认初始化为随机数。所以如果我们采用全局数组，那么可以不写a[0]=0 S[0]=0 s[0][0]=0

---

差分(前缀和的逆运算)

已知有数列a[1],a[2],a[3]...a[n] 构造数列b[1],b[2],b[3]...b[n]使得a[i]=b[1]+b[2]+...+b[i]，此时，b称为a的差分。

显然，a是b的前缀和，如果我们知道b数组，那么就在O(n)时间能求得a数组

差分的用途：看模板题797

当然，这里我们不需要细想如何去构造b数组，可以假想a数组全为0，然后不断+a1,+a2,+a3....得到的