【ACWING】 数论

1 求最大公约数（gcd）/欧几里得算法/辗转相除法

基于公式gcd(a,b) = gcd(b, a%b), 当b=0时，最大公约数是b本身

补充一点小细节，0与任何数的gcd等于这个数本身

int gcd (int a, int b)
{
    return b ? gcd (b, a % b) : a;
}

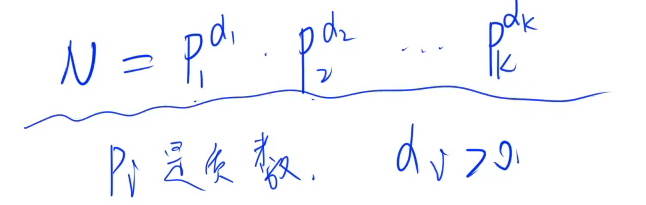
2 算术基本定理（公理）

所有整数都能够分解成若干个质因子乘积的形式

3 欧拉筛/筛法求素数

复杂度O(n)
算法演示视频

int primes[N], cnt, minp[N];    //primes存质数结果，cnt用来索引，minp[x]表示数x的最小质因子是什么
bool st[N];
// 产生从2-n-1的所有
void get_primes(int n )
{
    for(int i = 2; i < n; i ++)
    {
         if(!st[i])    // 如果i没有被筛掉，说明i是质数
         {
             primes[cnt++] = i;    //i存在primes里
             minp[i] = i;          // i这个数的最小质因子是他本身      
         }   
         for(int j = 0; 1LL*primes[j] * i <= n; j++)    // 遍历已经产生的质数数组，筛掉以他为最小质因子的合数
                                                        //（乘法那里有可能爆int，乘个1LL，转成LL，或者写成除法形式）
         {
              int t = primes[j] * i;
              st[t] = true;              // 筛掉合数
              minp[t] =  primes[j];      // 合数t的最小质因子是primes[j]
              if(i % primes[j] == 0) break;    // 合数只能被其最小质因子晒掉，不是最小质因子的时候，跳出循环
    }

}

4 约数和定理

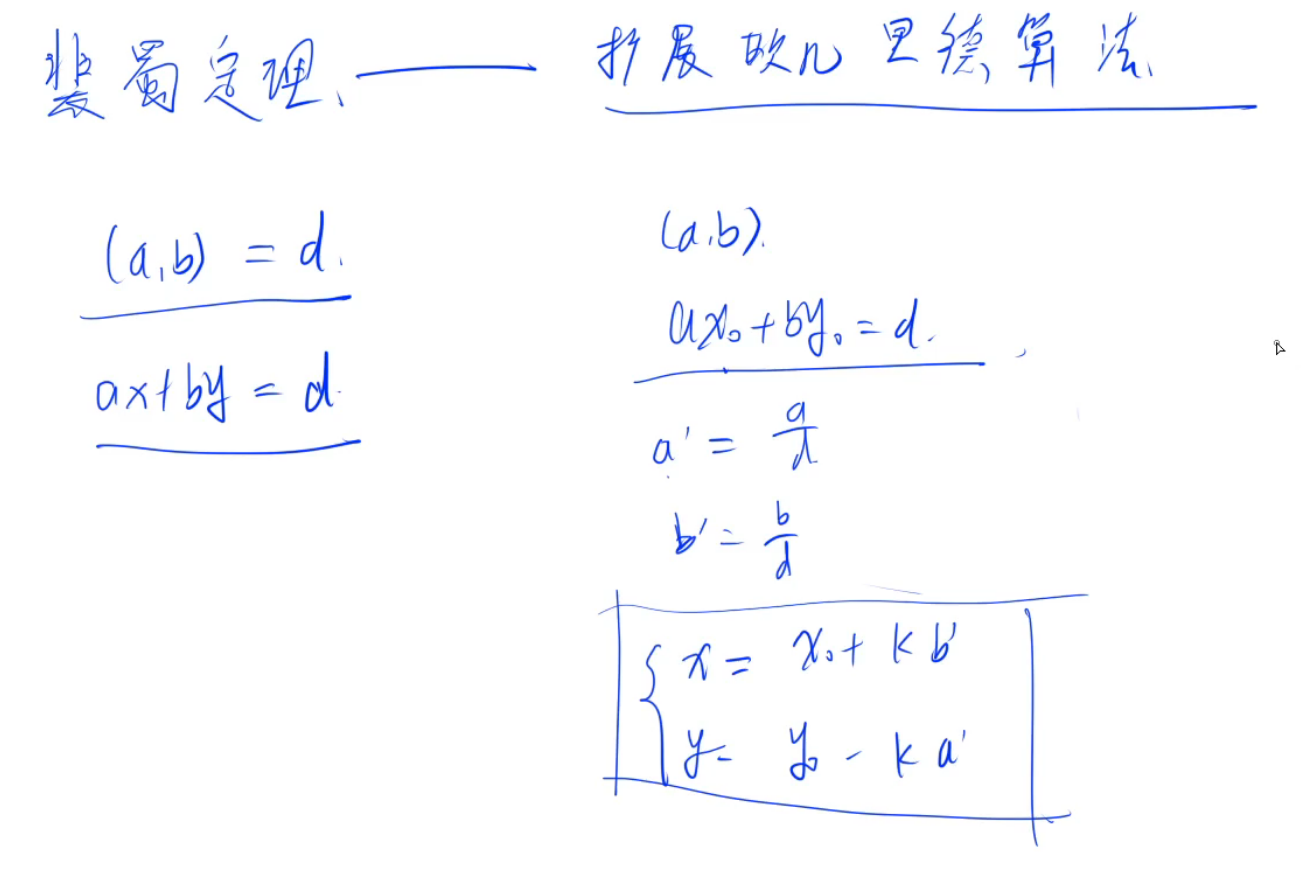
5 裴蜀定理/贝祖定理

对任何整数a,b，关于未知数x和y的线性丢番图方程(称为裴蜀等式):ax+by=c，方程有整数解当且仅当c是gcd(a,b)的倍数。裴蜀等式有解时必然有无穷多个解。

则必然有最大公约数d = gcd(a,b), 则必然存在一组整数（可以为负数）x，y满足ax + by = d

6 拓展欧几里得定理

该方法是用来求解gcd的，但是！ 他能够在求gcd的过程中，给出上面裴蜀定理的一组解

我们来分情况讨论一下扩展欧几里得定理：

1. 当b = 0时，a和b的最大公约数为a.则x = 1;
2. 当b ≠ 0时，by+(a mod b)x = gcd(a,b)
   ->by+(a - a/b * b)x = gcd(a,b)
   ->ax+b(y - a/b * x) = gcd(a,b)
   即当我们用扩展欧几里得定理求x和y时，欧几里得定理每递归一次x不用变,y->y-a/b * x即可
   如果我们求出x和y的一对，我们记为x0和y0
   那么其他的x和y可以通过x0，y0表示:
   令a’=a/gcd(a,b) , b’=b/gcd(a,b);

那么其他的x和y可以表示为：x=x0+kb’,y=y0-ka’;

求得一组解之后，能够很容易构造出通解的形式，如下图

int exgcd(int a, int b, int &x, int &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);    //辗转相除
    y -= a/b * x;
    return d;
}