【ACWING】 搜索和图论(一)

1 DFS BFS

1.1 对比

1. 两种算法都能对应一个搜索树，h表示树的深度，意味着根节点到这个一层要h步

2. 最优性当路径权重为1时，就是最短路

算法	数据结构	空间复杂度	最优性
DFS	stack	O(h)	无最优性
BFS	queue	O(2^h)	有最优性

BFS适合最短路求解，DFS适合对空间要求高的，或者各种奇怪的BFS解不了的

1.2 DFS

DFS可以当成栈理解，写题的时候想清楚搜索树就行。大多数DFS的题，都可以参考全排列问题的思路进行操作

其他的可能就涉及剪枝问题。

最优剪枝 或者 可行性剪枝

注意递归之后，一定要恢复递归前的现场

1.3 BFS

一层一层搜索，从距离根节点1开始，2，3...

2 树与图的存储

树是无环连通图，所以只理解图的存储就好了。

图分为无向图和有向图，但是我们可以在建立的时候，将无向图a-b表示为a->b a<-b，也就可以统一用有向图来存储

2.1 有向图的存储

1. 邻接矩阵（就是二维数组）-------g[a][b] == a->b,可以存权重值

比较少用，空间复杂度高(n^2)，不能存重复边。

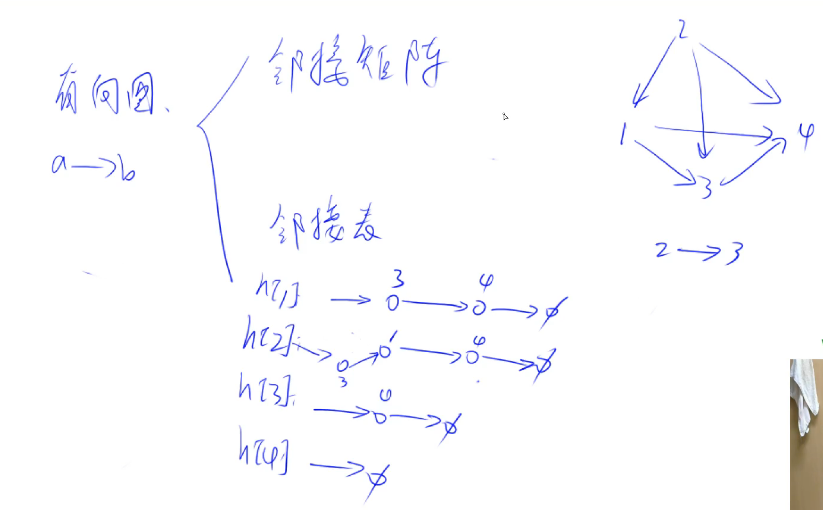
2. 邻接表（单链表）

比较常用，类似拉链法的hash存储

const int N = 100;
int h[N], e[N], ne[N], idx;
//h[N]是单链表头节点，e[]存值,ne[]存下一个节点索引
 
//邻接表添加元素都是头部节点添加
void add(int a, int b)
{
    //先存节点
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
 
int main(){
    //初始化，都指向空节点
    memset(h,-1,sizeof h);
    return 0; 
}

3 树与图的DFS

树和图的DFS/BFS时间复杂度为O(n+m)的，与点数和边数成线性关系

基于上面邻接表存储实现的DFS代码

//定义一个标志位，记录是否已经被访问过了
bool st[N];
 
void dfs(int u) //从u节点开始dfs
{
    st[u] = true;
    for (int i = h[u]; i!= -1; i =ne[i])
    {
        int j = e[i];
        if(!st[j]) dfs(j);
    }
}

4 树与图的BFS---按BFS队列框架写就行

5 拓扑排序

拓扑序列：若一个由有向图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列

拓扑序列是针对有向图的 有向无环图一定存在拓扑序列，有环必然没有拓扑序列，所以有向无环图也叫拓扑图