5.20学习总结

最优化基础理论与方法第四章 约束规划的最优性条件

4.1 基本概念

可行域：

 

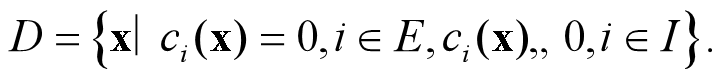
定义 4.1.1 对于约束规划问题 (4.1), 若对x^∗∈D，存在ε>0， 使得当x∈D，且‖x−x^∗‖⩽ε时，总有 f(x)⩾f(x^∗), 则称 x^∗为约束规划问题 (4.1) 的局部解, 或简称x^∗为解，若当 x∈D，且0<‖x−x^∗‖⩽ε时，总有 f(x)>f(x^∗), 则称x^∗为约束规划问题 (4.1) 的严格局部解。

定义4.1.2 对于约束规划问题(4.1),若对x^∗∈D,总有 f(x)⩾f(x^∗), 则称x^∗为约束规划问题(4.1)的全局解. 若当x∈D,x≠x^∗时，总有 f(x)>f(x^∗), 则称x^∗为约束规划问题(4.1)的严格全局解. 显然,全局解必是局部解,但反之不然.特别地,若D=R^n，则以上有关解的定义便是无约束规划问题相应解的定义.

4.2 约束规划问题局部解的必要条件

设x*是约束规划问题(4.1)的可行点，0≠d∈Rn. 若存在正数α使得

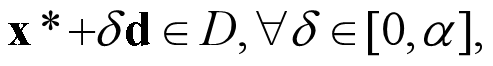
则称d为x*处的可行方向（Feasible Direction）.

记

 

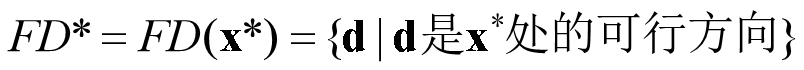
为x*处的全体可行方向的集合.

定义4.2.1 设x ̂是一般约束规划问题(4.1)的可行点. 当i∈I时,对某个约束, 若c_i(x ̂)=0, 则称c_i(x)⩽0为x ̂处的有效约束 ( activeconstraints); 若c_i(x ̂)<0，则称c_i(x)⩽0为x ̂处的非有效约束. 定义有效约束指标集 I(x ̂)={i∣c_i(x ̂)=0,i∈I}, 简称I(x ̂)为x ̂处的有效集(active set).

设x^∗是约束规划问题(4.1)的可行点, 定义 LD^∗=LD(x^∗)

 

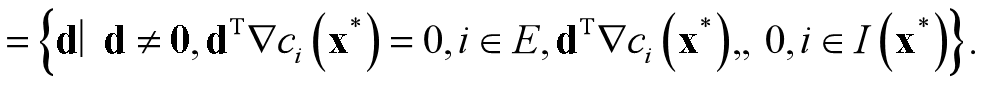
  显然, LD^∗∪{0}是一个锥, 称为x^∗处的线性化锥. 方便计算

在某些条件下,LD^∗=FD^∗。任何一个保证LD^∗=FD^∗成立的条件称为约束限制条件( constraint qualification). 在预备知识中谈过,对于目标函数f(x),若沿方向d的一阶方向导数小于0,则该方向是下降方向,记

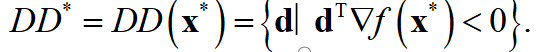
定理4.2.2 若x^∗是约束规划问题(4.1)的局部解,则

 

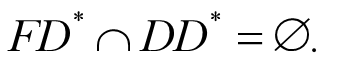
定理4.2.3(Farkas引理) 设 和 . 系统I :

 

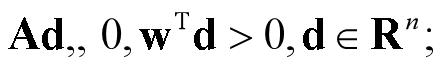
系统II:

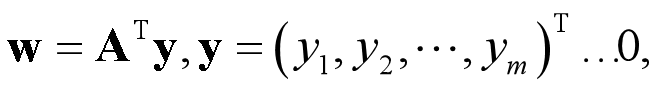
y⩾0表示y的每个分量 均大于等于0; 则两系统有且仅有一个有解.

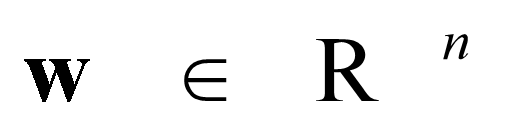
定理4.2.4 （约束问题局部解的一阶必要条件）设约束问题(4. 1)中的 f (x), ci(x)(i=1, 2, …, l+m)具有连续的一阶偏导数，若x*是约束问题(4. 1)的局部解，并且在x*处约束限制条件成立(即LD*=FD*)，则存在λ^∗=(λ_1^∗,λ_2^∗,…,λ_l+m^∗) ^T, 使得

 

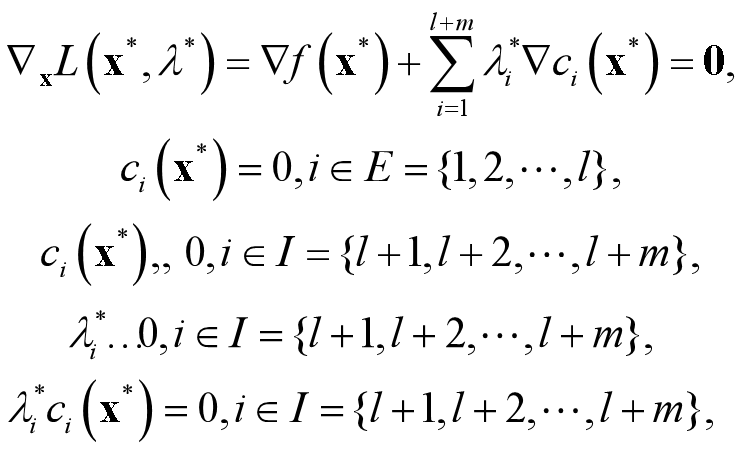
此条件又称为Kuhn-Tucker条件，简称K-T条件。对应点成为K-T点。 L为Lagrange函数，λ为x处的Lagrange乘子。

考虑：约束规划问题      min{f(x)=x_1^}; ■(&@&s.t.      c_1(x)=x_2^−x_1^3⩽0,@&c_2(x)=−x_2⩽0) x*=(0, 0)T 是约束问题的局部解，由前面例题可知LD*≠FD*, 约束限制条件不成立，x* 是不是K-T点。

Lagrange函数：

 

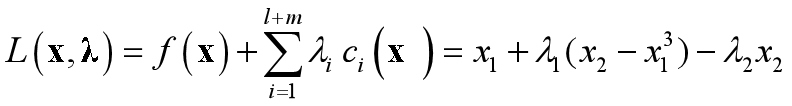
对于一切λ=(λ1,λ2)T,

 

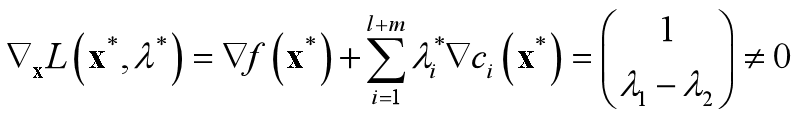
x*=(0, 0)T 不是K-T点。

定理4.2.5 若在约束问题(4. 1)的局部解x^∗处下述两条件之一成立: (1) 是线性函数; (2) 线性无关; 则在x^∗处有FD^∗=LD^∗

定理4.2.6 设x^∗是问题(4.1)的一个局部解， c_i(x)(i∈E∪I(x^∗))是 线性函数或 线性无关，则必存在λ^∗ ,使得K-T条件 (4.2.4)成立.

4.3 二阶充分条件

定理4.3.1(约束问题局部解的二阶充分条件) 考虑约束问题(4.1),设f(x),c_i(x)(i∈E∪I)具有连续的二阶偏导数.若存在x^∗满足下列条件: (1) K-T条件成立, 即存在 , 使得

 

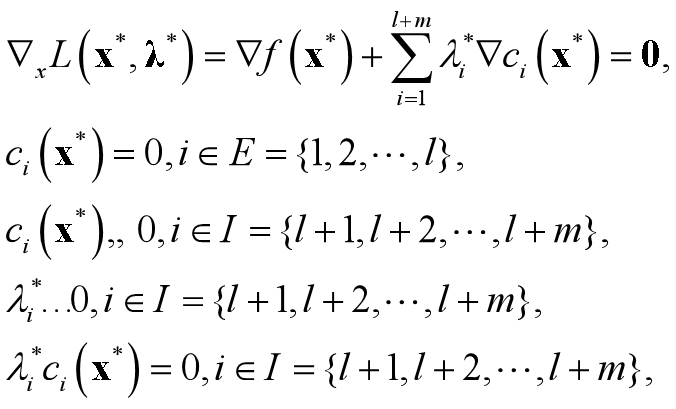
且λ_i^∗和c_i(x^∗)(i∈I)不同时为0(称为严格松弛互补条件);

(2)对于任意的d∈M,有

 

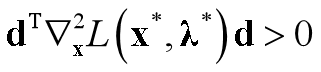
(4.3.1) 其中

 

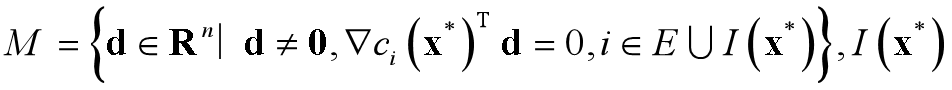
是x^∗处的有效约束指标集; 则x^∗是约束问题(4.1)的严格局部解.

4.4 凸规划的最优性条件

对于一般的非线性规划(4.1),若目标函数 f (x)是凸函数，可行域D是凸集，则称非线性规划(4.1)为凸规划。 若(4.1)中只含不等式约束，又ci(x) (i∈I)是凸函数，则 D是凸集。 对混合约束问题，若ci(x) (i∈E)是线性函数， ci(x) (i∈I)是凸函数，则D是凸集。

定理4.4.1 凸规划的局部解必是全局解. 定理4.4.2 设目标函数f(x)和约束函数c_i(x)一阶连续可微,并且c_i(x)(i∈E)是线性函数，c_i(x)(i∈I)是凸函数. 若凸规划(4. 1)的可行点x^∗是K-T点,则x^∗必是全局解.