5.17学习总结
最优化基础理论与方法第一章 最优化基础
1.1 最优化问题分类与实例
(1)最优化问题的数学模型:

![]() -- 决策变量, n 维列向量 n 维列向量
-- 决策变量, n 维列向量 n 维列向量 ![]()
![]() --目标函数 ci(x)=0 -- 等式约束 min--求目标函数极小值
--目标函数 ci(x)=0 -- 等式约束 min--求目标函数极小值
![]() -- 约束函数 ci(x)≤0 -- 不等式约束 s. t. – 受限于/受
-- 约束函数 ci(x)≤0 -- 不等式约束 s. t. – 受限于/受
可行域:
![]()
根据实际问题的不同要求, 最优化模型有不同的形式,都可以转换成前述一般的形式
例如, 对于求目标函数 f (x) 极大的问题 max f (x) 可转换成求- f (x) 极小的问题 min - f (x)
同样,对于不等式约束 ci(x) ≥ 0 可转换为 − ci(x) ≤ 0
(2)最优化问题分类:
① 约束/无约束优化
本质上,依据可行域 D进行划分:D ∈ Rn 无约束优化 D ∈ {x | ci(x)=0, i ∈ E ; ci(x) ≤ 0, i ∈ I } 约束优化
② 线性/非线性归化,二次非线性规划
线性规划:目标函数、约束函数都是变量x=(x1, x2, ⋯, xn)T 的线性函数。
二次规划:目标函数是变量x的二次函数,所有的约束函数都是x的线性函数
非线性规划:目标函数、约束函数中, 任有一个是变量x的非线性函数。 非线性最优化问题是最一般的最优化问题, 而线性规划和二次规划问题却是相当重要的特殊的最优化问题。
③ 离散/连续优化,整数/整数混合规划
离散最优化:可行域内点的个数有限 连续最优化:可行域含有无穷多个点,且点连续变化 整数规划:针对离散优化,变量均取整数 混合整数规划:针对离散优化,部分变量取整数,另一部分连续变化
④单/多目标规划
单目标归化:目标函数仅是一个数量函数
多目标规划:目标函数为向量函数
⑤ 其他分类:随机规划、模糊规划、确定规划等(自行了解)
1.2 线性代数基础知识
(1)线性空间基本定义
n维向量空间记为Vn , 空间中的元素为n维列向量 ,如下 x=(x1, x2, … , xn) T y =(y1, y2, … , yn) T
向量空间的基本运算为 和 x+ y = (x1 + y1, x2 + y2, … , xn + yn) T 数量乘 λx = (λ x1, λ x2, … , λ xn) T
若两种基本运算满足下列8个条件:
① x+y=y+x
② (x+y)+z=x+(y+z);
③ 存在一个0元, 使得0+x=x;
④ 存在−x∈V,称为x的负元,使得x+(−x)=0;
⑤ 1x=x
⑥ λ(μx)=(λμ)x
⑦ (λ+u)x=λx+ux
⑧ λ(x+y)=λx+λy
则称Vn为实数域上的线性空间
设 α1, α2,⋯,αn 为Vn 中 的n个向量则称 x = λ1α1 + λ2 α2 +⋯+ λn αn 为α1, α2,⋯,αn 的线性组合
若:存在不全零的 λi 满足 λ1α1 + λ2 α2 +⋯+ λn αn =0 则称 α1, α2,⋯,αn 线性相关, 否则, 线性无关
(2)线性空间的基与维数
定义1:在线性空间 Vn 中,如果存在 n 个元素 α1, α2,⋯,αn 满足:
(1) α1, α2,⋯,αn 线性无关;
(2) V中任一元素α 总可由α1, α2,⋯,αn可线性表示; 那么,α1, α2,⋯,αn 就称为线性空间Vn的一个基 ,n为线性空间的维数
定义2
![]()
![]()
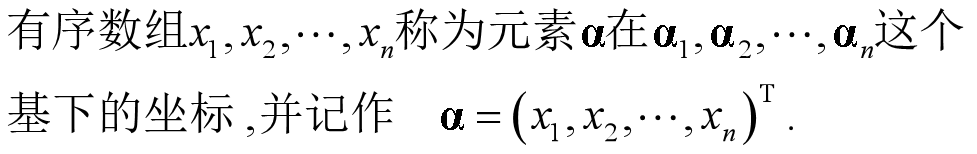
(3)欧氏空间
定义:两个n 维向量
![]()
![]()
![]()
![]()
定义了内积的n维实向量空间R称为n维欧氏空间
向量的内积具有如下基本特性:
![]() 交换律
交换律
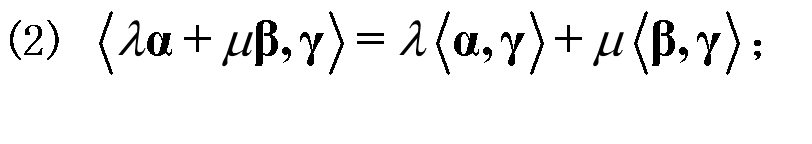 分配律
分配律
![]()
![]() 非负性
非负性
n维欧式空间中向量的长度(2范数)定义为
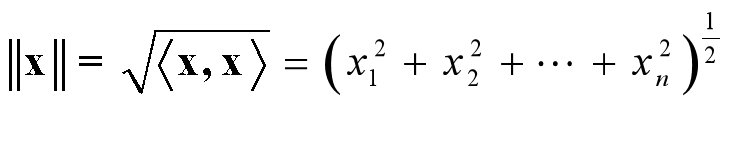
向量长度的性质:
![]()

![]()
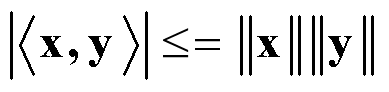
![]()
设x, y为两个向量,若⟨x,y⟩=0, 则称x, y正交,记作x⊥y
如果欧氏空间V中不含零向量的向量组中的向量两两正交,则称该向量组为一个正交向量组。
如果正交向量组中每个向量都是单位向量,则称其为单位正交向量组(或称标准正交向量组).
(4)矩阵
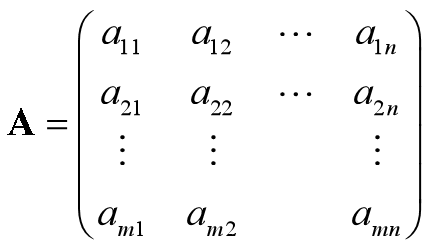
为m×n矩阵,记为Am×n
① 矩阵的秩记为 rank(A) 若 rank(A) = min{m, n} 则 称A为满秩矩阵
② 若m=n,A为方阵,若满秩, 则A为非奇异矩阵 若方阵A满足 AT=A,称其 为对称方阵 对于任意向量x≠0,方阵A均满足 xT Ax > 0 称A为正定矩阵 xT Ax ≥ 0 称A为半正定矩阵
矩阵的初等变换: (1)互换矩阵的两行(列); (2) 用一个非零常数乘以矩阵的某一行(列); (3)将矩阵某一行的k倍加到另一行上去(列);
矩阵秩的定义:设在矩阵A中有一个不等于0的r阶子式D 且所有r1阶子式(如果存在的话)全等于0 那么D称为矩阵A的最高阶非零子式 数r称为矩阵A的秩 记作rank(A) 并规定零矩阵的秩等于0
矩阵秩的计算:任何矩阵经过有限次初等行(列)变换将它变为最简行(列)梯形阵,梯形矩阵中非零行(列)的行(列)数 记为矩阵的秩。
矩阵的特征值及特征向量
定义: 设A为n阶方阵, λ是一个数, 若存在非零列向量x ,使得
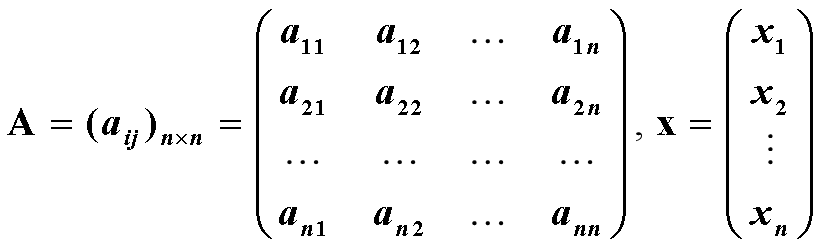
则称 λ 为 A 的一个特征值,非零向量x 称为矩阵 A 的对应于特征值λ的特征向量,简称为 A 的特征向量。
特征值与特征向量的方法:
第一步: 令特征多项式
![]() 求特征值
求特征值![]()
第二步: 对于每一个![]() 求
求![]() 基础解系.
基础解系.
第三步: 基础解系的非零线性组合为A对应于![]() 的全部特征向量.
的全部特征向量.
行列式计算方法总结
方法一:化上三角行列式
这是求行列式的最基础的方法,一般就是一列(行)乘上一个数加到某一列(行),使其转化为上(下)三角形行列式。
方法二:连加法
特征:当你发现行列式每一行(列)的值加起来都相等且不等于0时,试试把他们其余行(列)全部加到第一行(列)去,然后再把这个和提出来,从而第一行(列)就全是1了,从而简化行列式。
方法三:滚动消去法
特征:当你发现,相邻的行(列)长得比较相似,很多项长得一样时。不妨试试滚动相减。即:最后一行(列)开始的每一行(列)都减去上一行(列)。
四:逐行(列)相加减法
该方法是将第一行(列)加(减)到第二行,获得的新的第二行再拿去加(减)第三行。
特征:发现前(后)一行(列)中的元素如果去掉“某个元素”后,再和下一行(列)相加减,就能把下一行(列)的某些元素消去,而不带来新的元素。并且前一行(列)中的那个想要去掉的 “某个元素” 能用同样的方法事先先消掉。
当然值得注意的是:从最后一行开始和从第一行开始,结果往往会不一样,需要读者在做题的时候,选择好到底应该从哪开始。
五:拆分行列式
把一个行列式拆成几个好算的行列式之和
特征:来个简单点的自己感受
六:直接按一行(列)展开
七:按拉普拉斯公式,多行展开
在算矩阵时,可挖洞后再算,以简化计算。
八:加边法
当每一行有较多相同元素时,可考虑按一行展开的反向操作,加多一行,然后用新加的行去减其他的行,来简化行列式
九:加边法和范德蒙德行列式一起用
方法十:归纳法
该方法多用于证明行列式的值等于某个式子,或对于已经知道结果的行列式使用。同数学归纳法。先证明阶为2 时成立,再从 n-1成立推出n阶也成立。
方阵特征值的性质
1)![]() 为
为![]() 的特征值.
的特征值.
2)![]() 为
为![]() 的特征值
的特征值
3)![]() 为
为![]() 的特征值.
的特征值.
![]()
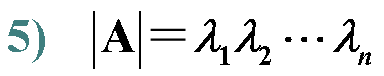
![]()
![]()
相似矩阵:A与B为n阶方阵,若存在一个可逆矩阵 使得![]() 称A与B相似,记作
称A与B相似,记作![]()
若:方阵A与B相似,则A与B有相同的特征值.
若:A相似于一个对角形矩阵, 则称A可对角化.
定理:方阵A相似于一个对角形矩阵的充要条件:A有n个线性无关的特征向量.
推论1:设n阶方阵A有n个互异的特征值λ1,λ2 ,⋯,λn , 则A~diag(λ1,λ2 ,⋯,λn ).
推论2:n阶方阵A与对角形矩阵相似的充要条件是对于每一个n_i重特征值λ_i,矩阵(λ_iI−A)的秩为n−n_i。
1.3 多元函数分析
(1)梯度
定义:设n元函数f(x)对自变量x=(x1, x2, …, xn)T 的各分量xi的偏导数(i=1, 2, …, n)都存在,则称函数
![]()
f(x)在x处一阶可导,并称向量 为函数f(x)在x处的一阶导数或梯度。
梯度几何意义
函数在一点的梯度垂直于该点等值面(或等值线) ,指向函数增大的方向.
(2)Hesse矩阵
定义:设n元函数f(x)对自变量x=(x1, x2, …, xn)T 的各分量xi的二阶偏导数∂^2f(x)/∂x_i∂x_j(i=1, 2, …, n; j=1,2, …, n)都存在,则称函数f(x)在x处二阶可导,并称矩阵
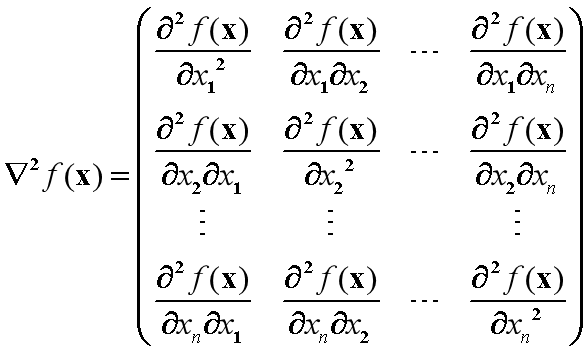
为函数f(x)在x处的二阶导数或Hesse矩阵。
若 f (x) 对x 各变元的所有二阶偏导数都连续,
├ ∂^2f(x)/∂x_i∂x_j=├ ∂^2f(x)/∂x_j∂x_i
此时,∇^2f(x) 为对称矩阵
(3)Jacobi矩阵
定义:设向量函数F(x)= ( f1(x), f2(x), …, fm(x)) 的各分量函数fi(x) (i=1, 2, …, m)对自变量x=(x1, x2, …, xn)T 的各分量的偏导数 ├ ∂f_i(x)/∂x_j, i=1,2, …, m; j=1,2, …, n 都存在,则称F(x)在点x处一阶可导,并称下面矩阵为向量函数F(x)在x处的Jacobi矩阵
Jacobi矩阵

(4)方向导数
若函数![]() 在点
在点![]() 处可微,则函数
处可微,则函数![]() 在点
在点![]() 处沿任一方向
处沿任一方向![]() 的方向导数存在,且
的方向导数存在,且
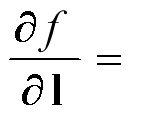
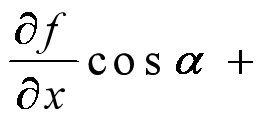
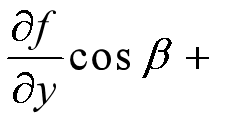
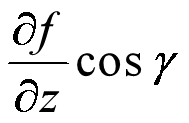
其中, 各导数∂f/∂x, ∂f/∂x, ∂f/∂x均为在点![]() 处的值.
处的值.

方向导数几何意义:函数f(x) 在x ̅处沿d(单位化:l=d/||d||)方向的变化率。 若∂f/∂d>0, 沿方向d增加时,函数数值上升; 若∂f/∂d<0, 沿方向d增加时,函数数值下降; 若方向d=∇f(x ̅) 是在x ̅处使得方向导数达到最大的方向,称其为最快上升方向。 若方向d=−∇f(x ̅) 是在x ̅处使得方向导数达到最小的方向,称其为最快下降方向。
二阶方向导数及几何意义
定义:设n元函数f(x)具有连续的二阶偏导数,则它在x ̅处沿方向d处的二阶方向导数为
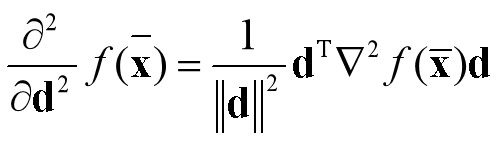
几何意义:描述函数f(x)在x ̅处沿方向d的凹凸性和弯曲程度。
(5)n元函数的Taylor展开
定理1.3.3 (1) 设函数 f(x): Rn→R. 若f(x)在点x ̅处的某个邻域N(x ̅)内一阶连续可微,则存在𝜽∊(0, 1), 使得 (拉格朗日中值定理)
![]()
(2) 设函数 f(x): Rn→R. 若f(x)在点x ̅处的某个邻域N(x ̅)内一阶连续可微,则 :
![]()
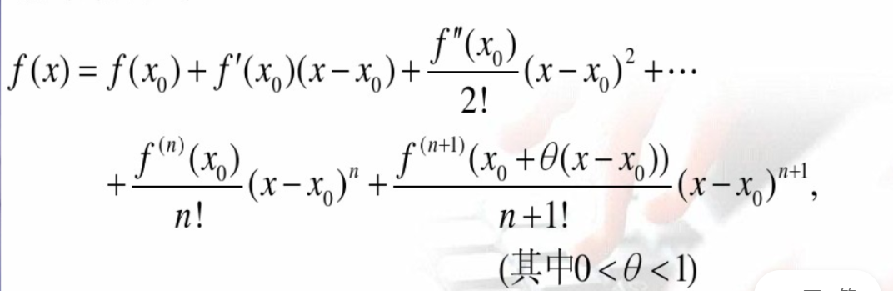
(3) 设函数 f(x): Rn→R. 若f(x)在点x ̅处的某个邻域N(x ̅)内二阶连续可微,则存在𝜽∊(0, 1), 使得:
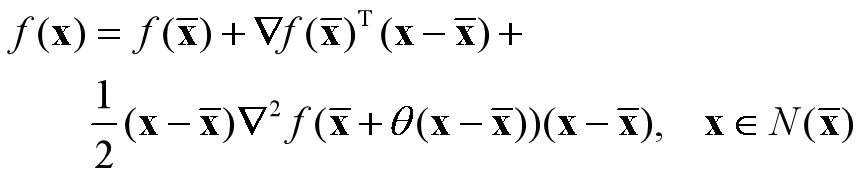
(4) 设函数 f(x): Rn→R. 若f(x)在点x ̅处的某个邻域N(x ̅)内二阶连续可微,则 :
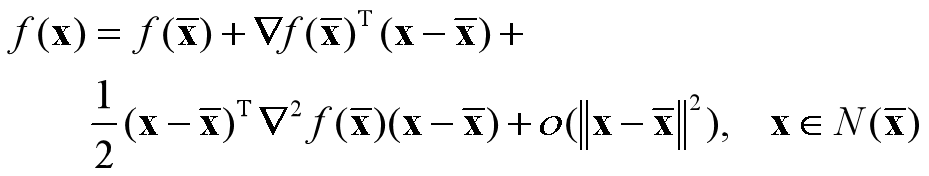
1.4 凸集与凸函数
(1)定义
凸集和凸函数在非线性规划的理论中具有重要作用,下面给出凸集和凸函数的一些基本知识。
定义1 设集合D ∊Rn,若对D 中任意两点x 和y,连接这两点的线段仍属于D;换言之,对于任意x ,y ∊ D, ∀α[0,1], 恒有 α x+(1- α )y ∊ D 则称集合D为凸集
几何意义:若两点属于此集合,则两点连线上的任意一点均属于此集合。
(2)性质
定理1.4.1: 设D1, D2 ∈Rn是凸集,α∊R, 则
![]()
![]()
![]()
![]()
定理1.4.2: D是凸集的充分必要条件是:对任意的m≥2, 任意给x1, x2, …, xm ∊ D 和 实数α1, α2,…, αm, 且αi ≥0 (i=1, …,m; ∑_i=1^m▒α_i),均有
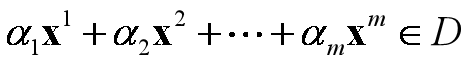
证明:数学归纳法,见教材18页
定义1.4.2: 给定凸集D⸦Rn,x∊Rn. 若存在x的δ邻域N δ(x)={y | ||y-x|| < δ } ⸦D,则称x为D的内点;所有内点组成的集合记为intD. 若x的任意δ邻域中既包含D中的点,又包含不属于D的点,称x为D的边界点;所有边界点组成的集合记为∂D. 若对任意δ>0均有N δ(x)∩D≠ϕ, 则称x属于集合D的闭包,记为x ∊clD. 根据以上定义可知,集合D的闭包clD= DU ∂D, 它是包含集合D的最小的闭集.
定理1.4.3: 设D1,D2是两个非空集合, α ∈ Rn,β ∈R, 若有
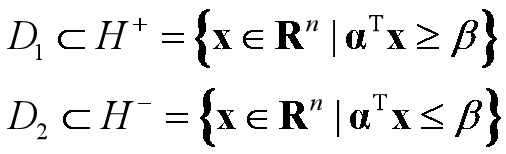
称超平面H={x∈R^n| α^Tx=β}分离集合D1和D2. 进而,若有D1UD2 ⊄H,则称H正常分离D1和D2. 若有
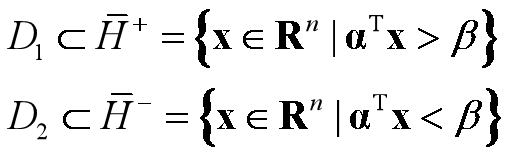
则称H严格分离D1和D2.
定理1.4.3(投影定理,自行学习): 设D⊂R^n是非空闭凸集, y ∈ Rn, y∉D,则
(1)存在唯一的点x ̅ ∈D,使得x ̅是y到D的距离最小的点,即
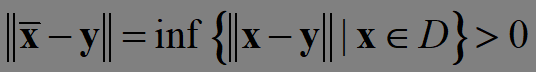
其中,inf 为下确界。 (2) x ̅是y到D的距离最小的点的充要条件是
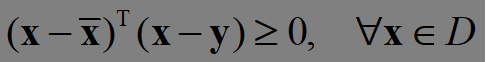
(3)凸函数

若有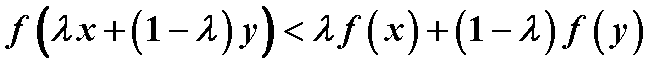 则称 f (x) 为凸集D上的严格凸函数。
则称 f (x) 为凸集D上的严格凸函数。
若 −f(x)为凸函数,则称 f 为凹函数; 若若 −f(x)为严格凸函数,则称 f 为严格凹函数
凸函数几何意义: 当x为单变量时,凸函数的任意两点间的曲线段总在弦的下方,凹函数总在弦的上方
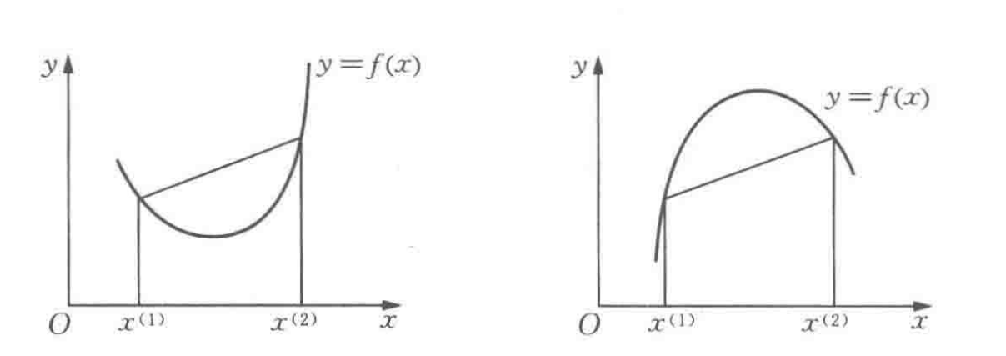
下列函数在 Rn 上的凸函数:
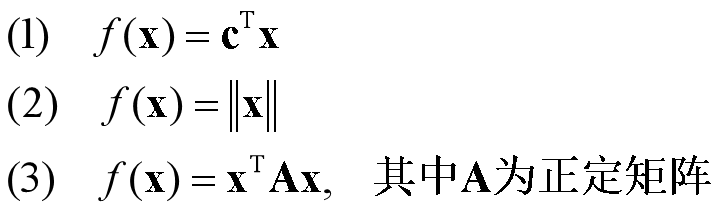
凸函数性质

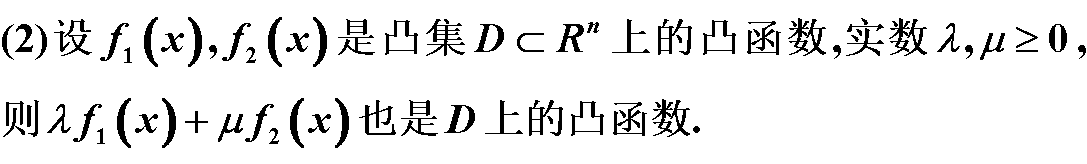
定义1.4.5 设 f (x) 是定义在 D ⊂R^n上的函数, α∈ R ,集合
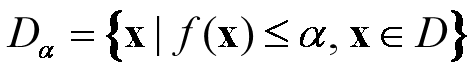
称为函数 f 的 α 水平集。
凸函数判别定理:
定理1.4.7 f(x) 是凸函数的充要条件是对任意的x,y ∈ R^n,一元函数 φ(α) = f(x+ αy) 是关于的α凸函数。
凸函数判别定理: 定理1.4.8 设 D⸦Rn 是非空开凸集,f :D⸦ R^n→R,且f(x) 在D上一阶连续可微,则 (1) f(x) 是D上的凸函数的充要条件是 f(y) ≥ f(x) + ∇ f(x)T(y-x),∀x, y ∈ D (2) f(x) 是D上的严格凸函数的充要条件是 f(y) ≥ f(x) + ∇ f(x)T(y-x),∀x, y ∈ D, 且x ≠ y
凸函数判别定理: 定理1.4.9 设 D⸦Rn 是非空开凸集,f :D⸦ R^n→R,且f(x) 在D上二阶连续可微,则f(x) 是D上的凸函数的充要条件是f(x) 的Hesse矩阵 ∇2 f(x) 在D上是半正定的。 定理1.4.10 设 D⸦Rn 是非空开凸集,f :D⸦ R^n→R,且f(x) 在D上二阶连续可微, 如果f(x)的Hesse矩阵 ∇2 f(x) 在D上是正定的,则f(x)是D上的严格凸函数; 反之,如果f(x)是D上的严格凸函数,则 ∇2 f(x) 在D上是半正定的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号