tarjan（割点，割边）

割点 ：删掉这个点和这个点有关的边,图就不是连通图,分裂成为了多个不相连的子图

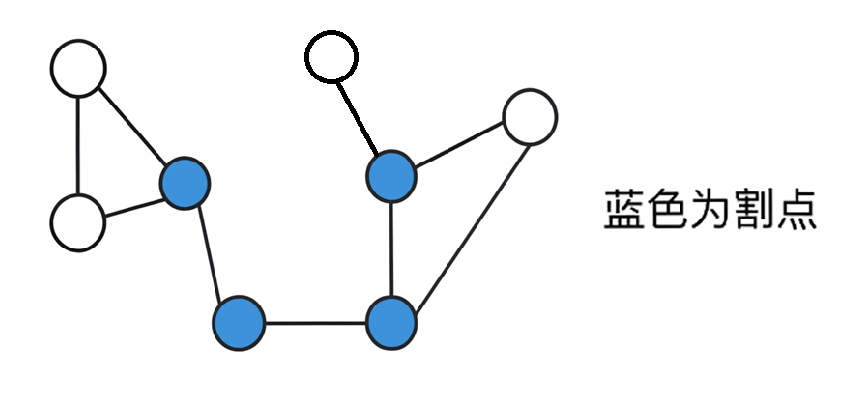
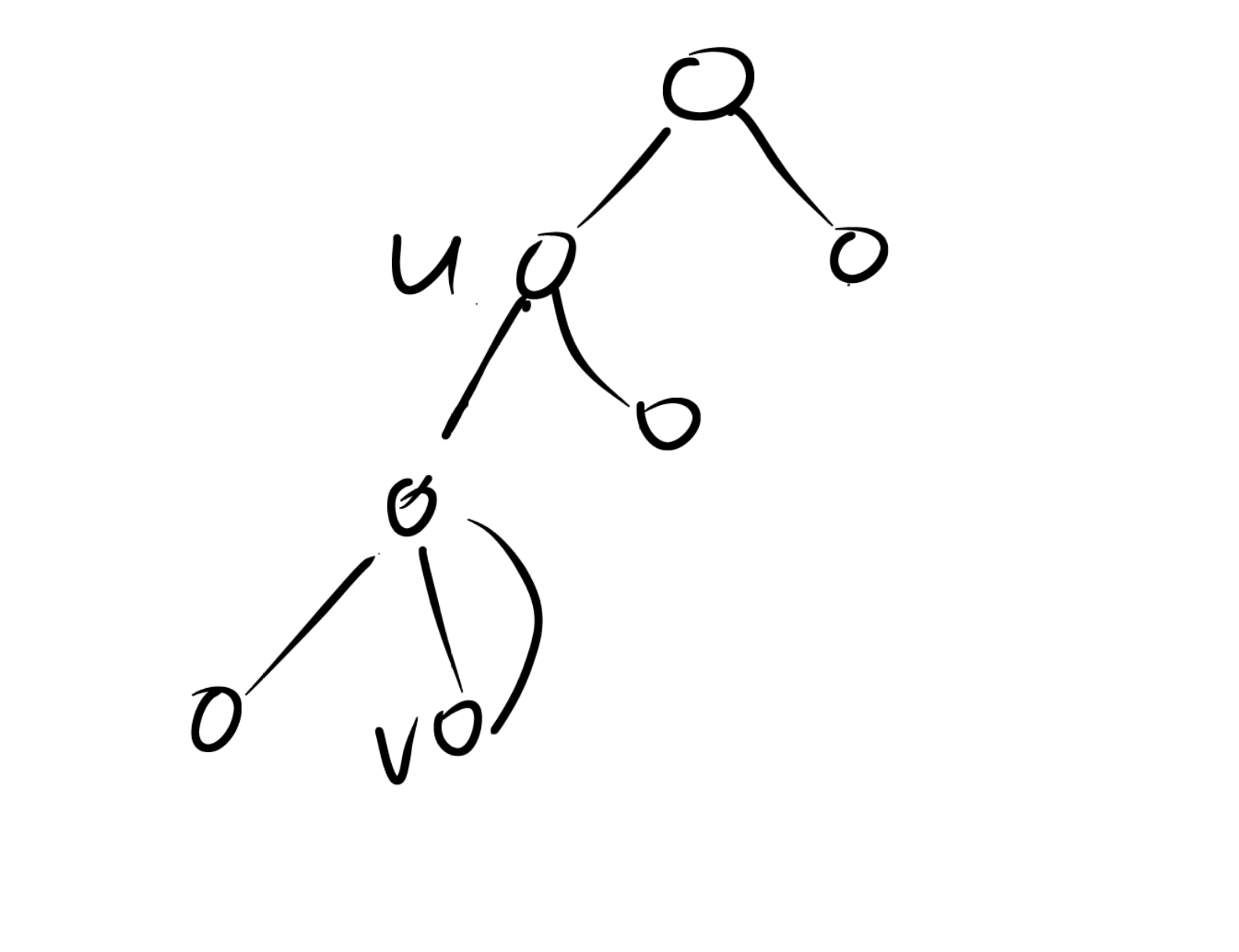
判断方法：如果有点v， u（非根结点）满足 dfn(u)<=low(v)，那么就可以说u是一个割点
如果 u是根的话，那么还要保证他至少有两个儿子
可以这么想，如果v这个点走一条返祖边所能到达的最远的点，都在u的后面，那我必须走u才能到根节点，我把u删掉后，v就走不到根节点了，图不联通了，所以u是一个割点

割边：删掉这个边，图就不是连通图,分裂成为了多个不相连的子图

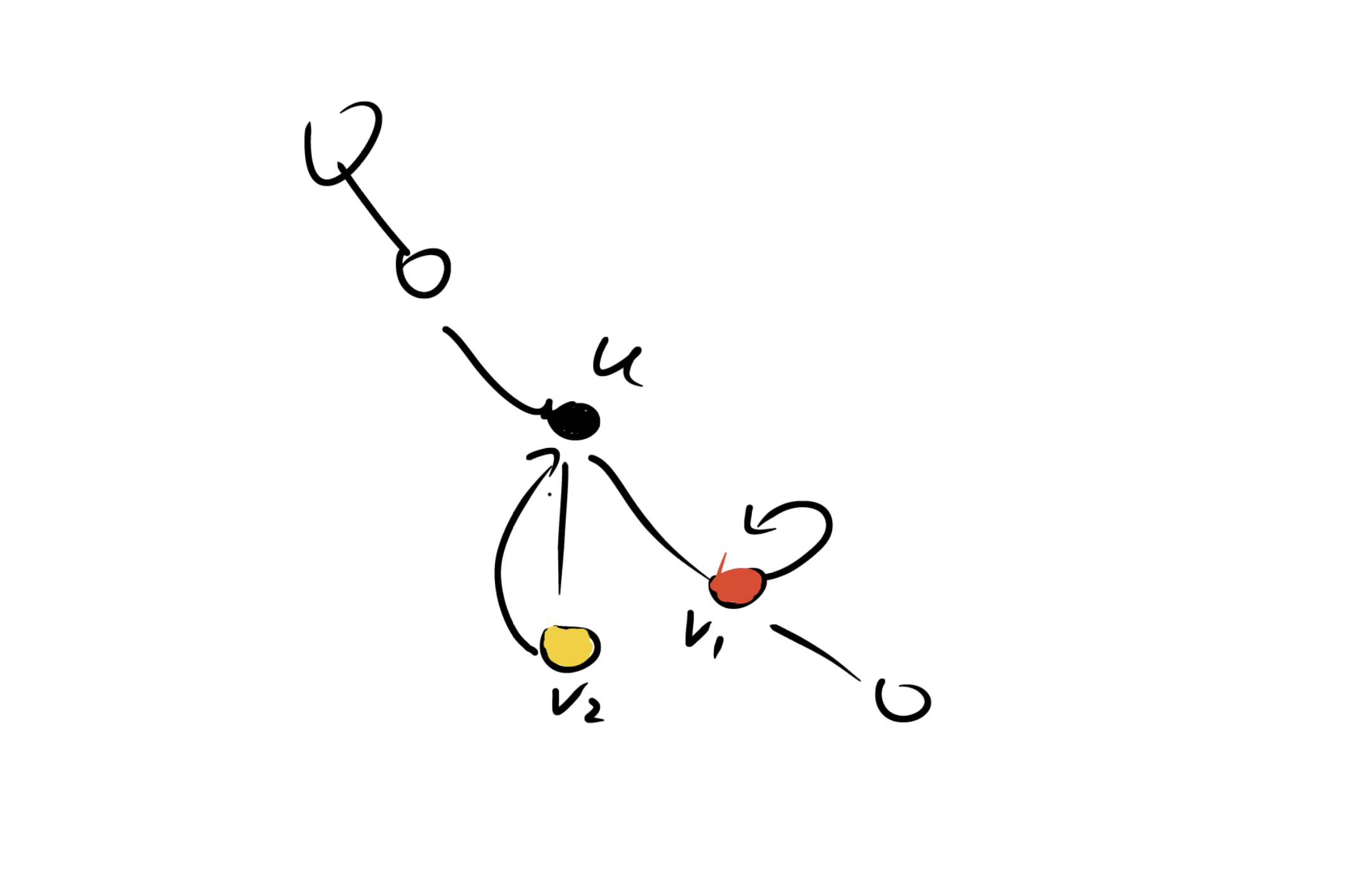
判断方法：如果存在v，u满足dfn(u)<low(v)，那么就可以说u-v是一条割边
割点和割边唯一的区别就是取等问题
看图，low(v1)<dfn(u)，删去u-v1分成两个子图，low(v2)=dfn(u)，我即使删去这个u-v2，图依然联通

特别注意：

在无向图中
low(v)=min(low(v),dfn(u))，他会尝试去更新dfn(u)的值，
如果更新到dfn(u)的话，对于割点来说dfn(u)<=low(v)，是没有影响的，但是对于割边dfn(u)<low(v)，却会少计算割边

模板割点
代码

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
#define swp(a,b) a^=b^=a^=b
const int N=2e5+10;
using namespace std;
vector<int>e[N];
int dfn[N],low[N],tim=0,rt;
int n,m;
int tot=0,cut[N];
bool cmp(int x,int y){
	return x<y;
}
void dfs(int f,int x){
	int cnt=0;
	dfn[x]=low[x]=++tim;
	for(int i=0;i<e[x].size();i++){
		int y=e[x][i];
		if(y==f)continue;
		if(!dfn[y]){
			cnt++;
			dfs(x,y);
			low[x]=min(low[x],low[y]);
			if(low[y]>=dfn[x]){
				if((x==rt&&cnt>=2)||(x!=rt)){
					cut[x]=1;
				}
			}
		}else{
			low[x]=min(low[x],dfn[y]);
		}
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int x,y;
		cin>>x>>y;
		e[x].push_back(y);
		e[y].push_back(x);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			rt=i;
			dfs(0,i);
		}
	}
	for(int i=1;i<=n;i++){
		if(cut[i])tot++; 
	}
	cout<<tot<<endl;
	for(int i=1;i<=n;i++){
		if(cut[i])cout<<i<<" "; 
	}
	return 0;
}

割边

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;

vector<int> e[N];
int dfn[N], low[N], tim;
vector<pair<int, int>> b;
int n, m;

void tarjan(int f, int x) {
    dfn[x] = low[x] = ++tim;
    for (int y : e[x]) {
        if (y == f) continue;
        if (!dfn[y]) {
            tarjan(x, y);
            low[x] = min(low[x], low[y]);
            if (low[y] > dfn[x]) {
                int a = min(x, y);
                int bb = max(x, y);
                b.push_back({a,bb});
            }
        } else {
            low[x] = min(low[x], dfn[y]);
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; ++i) {
        int x, y;
        cin >> x >> y;
        e[x].push_back(y);
        e[y].push_back(x);
    }

    for (int i = 1; i <= n; ++i) {
        if (!dfn[i]) {
            tarjan(-1, i);
        }
    }

    sort(b.begin(), b.end());

    for (int i=0;i<b.size();i++) {
        cout << b[i].first << " " << b[i].second << "\n";
    }

    return 0;
}