tarjan算法

给你一个图求强连通分量

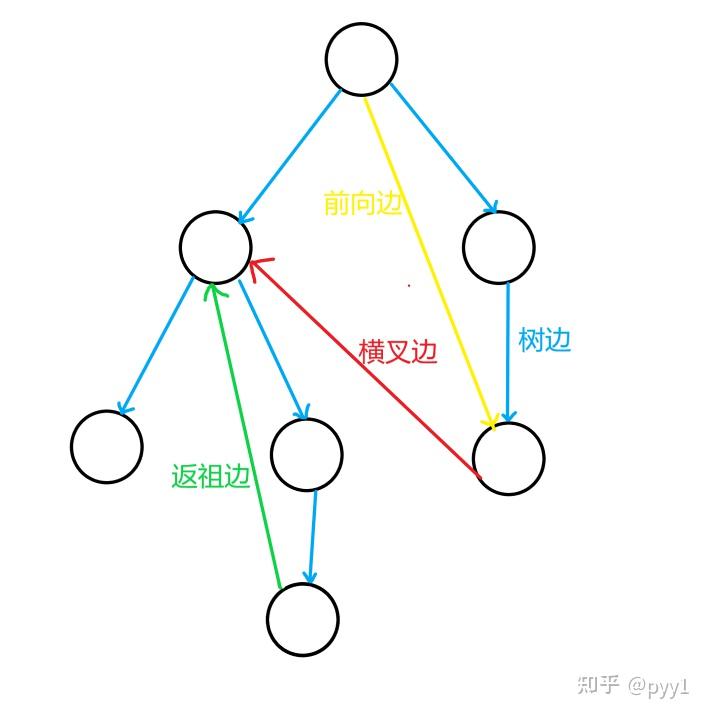
首先明确一点返祖边，横叉边，前向边。

1. 返祖边，首先自如其名就是，从下向上能走到他祖先的边。就是返祖边。
2. 横叉边，指向一个不是他的祖先也不是他的孩子节点的一条边就是横叉边。
3. 前向边。就是指向他的孩子节点的一条边就是前向边。

• tarjan 算法的核心，dfn和low

Dfn就是时间戳。就是你去对这个图进行DFS搜索的时候。第几个到达的节点，那么这个点的dfn就是他的顺序点。

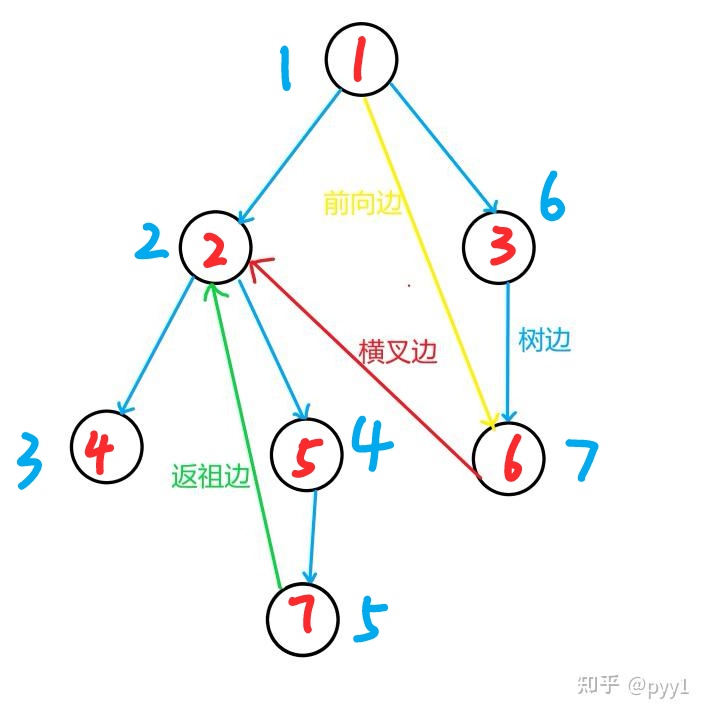
红色的是这个点的编号，蓝色点的是这个点的dfn。

low是这个点。走一条返祖边能到达的dfn最小的点，也就是走一条返祖边能走到最远的祖宗节点。

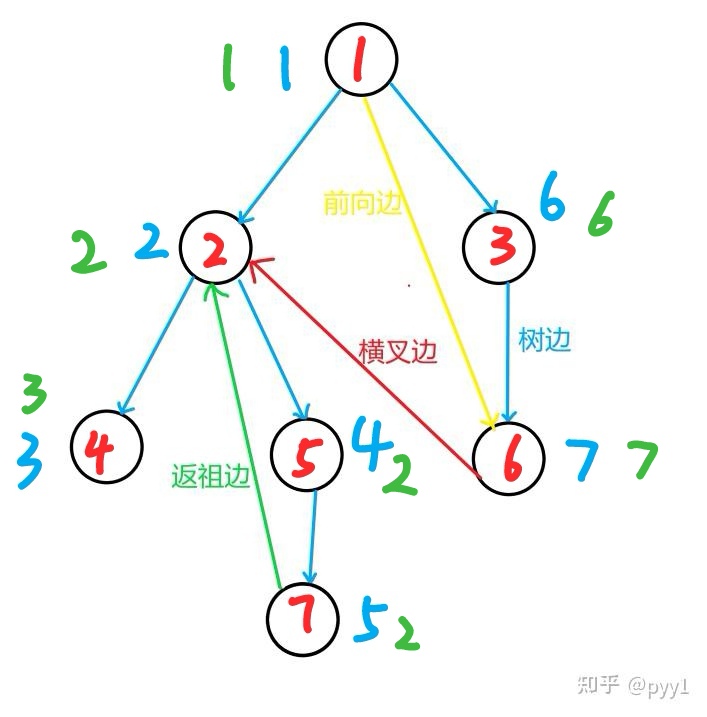
在这幅图中绿色的是它的low值，只有5号节点可以走到他的儿子节点7。然后走一条返祖边到达2，所以5号节点的low值。七号节点可以走一条返祖边到2，所以7号节点的low是2.

tarjan算法思路

1. 用一个stack去存你去做dfs的时候，每个点的前置节点。并计算出每一个点的Dfn和low。
   dfn[u]=low[u]=++tim
   更新low，需要分类讨论

2. 对于一个点，出边所连的节点如果是这个stack内已经存在的节点那么它形成了一个环，那么这个点的low值的计算方式是
   low[u]=min(low[u],dfn[v])

3. 对于一个点,如果他在回溯的过程中那么它的low的计算方式是
   low[u]=min(low[u],low[v])

如果存在一个点的,dfn=low.那么它一定是某一个强连通分量的起始节点。那么从这个点包括这个点往后的属于这个强连通分量的节点他的low都是等于这个节点的dfn,那么这一部分我们可以给他弹出战,标记成一个强连通分量。

所以我们可以在回溯的过程中去计算完low的同时去判断这个点能否作为以某一个强联通分量的起点。如果可以的话，那么我从栈顶依次弹出，一直弹到这个节点都是同一个强连通分量里的节点。

思考。会不会我在stack中的某一个强连通分量的起点后面，还会有一个强连通分量。
显然是不会的。我是在回溯的过程中去计算这个过程，也就是在这个点后面的值我都已经计算完了，所以在这点的后面不存在还会有另外一个强连通分量。`
at-scc模板

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
#define swp(a,b) a^=b^=a^=b
const int N=1e7+10;
using namespace std;
vector<int >e[N];
int n,m;
int dfn[N],low[N],tim=0;
int ins[N];
int p[N];
vector<int >scc[N];
int id=0;
stack<int >s;
void tarjan(int x){
	dfn[x]=low[x]=++tim;
	ins[x]=1;
	s.push(x);
	for(int i=0;i<e[x].size();i++){
		int y=e[x][i];
		if(!dfn[y]){
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}else if(ins[y]){
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(dfn[x]==low[x]){
		++id;
		scc[id].push_back(x);
		p[x]=id;
		while(s.top()!=x){
			int u=s.top();
			s.pop();
			scc[id].push_back(u);
			p[u]=id;
			ins[u]=0;
		}
		ins[x]=0;
		s.pop();
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int x,y;
		cin>>x>>y;
		e[x+1].push_back(y+1); 
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i])tarjan(i);
	}
	cout<<id<<endl;
	for(int i=id;i>=1;i--){
		cout<<scc[i].size()<<" ";
		for(int j=scc[i].size()-1;j>=0;j--){
			cout<<scc[i][j]-1<<" ";
		}
		cout<<endl;
	}
	return 0;
}