牛客寒假训练二（上）

按照做题、解题和补提的顺序。

一、H题（签到）

https://ac.nowcoder.com/acm/contest/9982/H

速度有点慢，所以A一题就排名到了一千之后

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;
int aa[1002][1002];
int main() {
    int n;
    cin >> n;
    char p;
    string s1 = "";
    for (int i = 0; i < n; i++) {
        if (i % 2 == 0)p = '0';
        else p = '1';
        s1 += p;
    }
    string s2 = "";
    for (int i = 0; i < n; i++) {
        if (i % 2 == 1)p = '0';
        else p = '1';
        s2 += p;
    }
    for (int i = 0; i < n; i++) {
        if (i % 2 == 0)cout << s1 << endl;
        else cout << s2 << endl;
    }
}

 

 

二、J题（强思维）

https://ac.nowcoder.com/acm/contest/9982/J

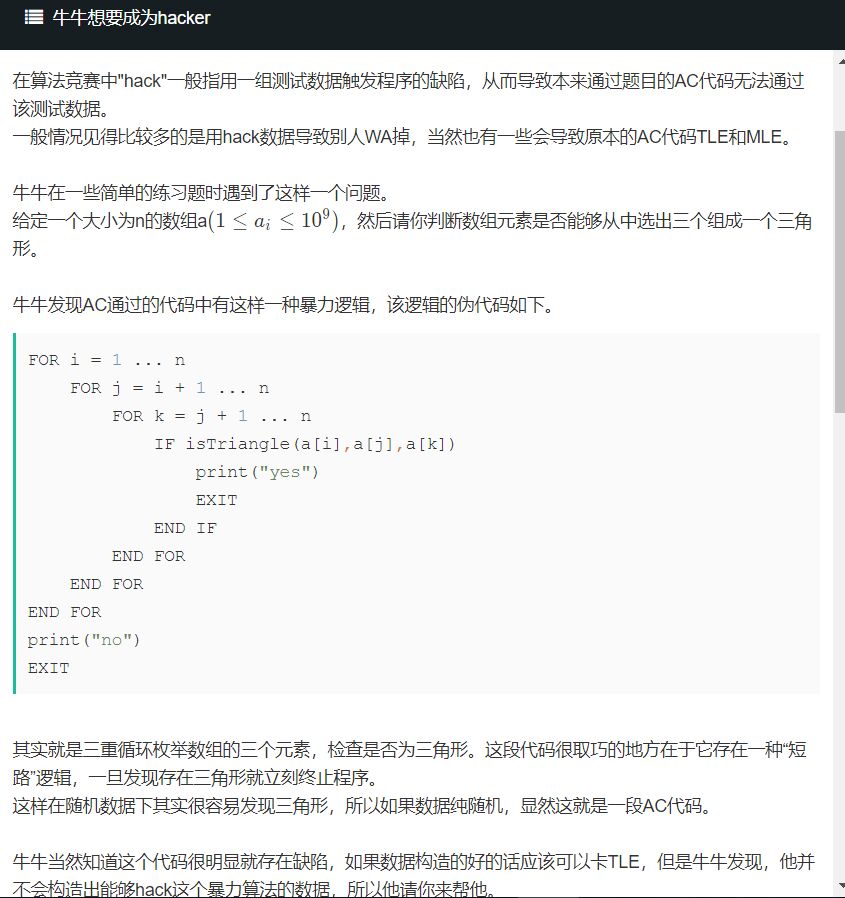
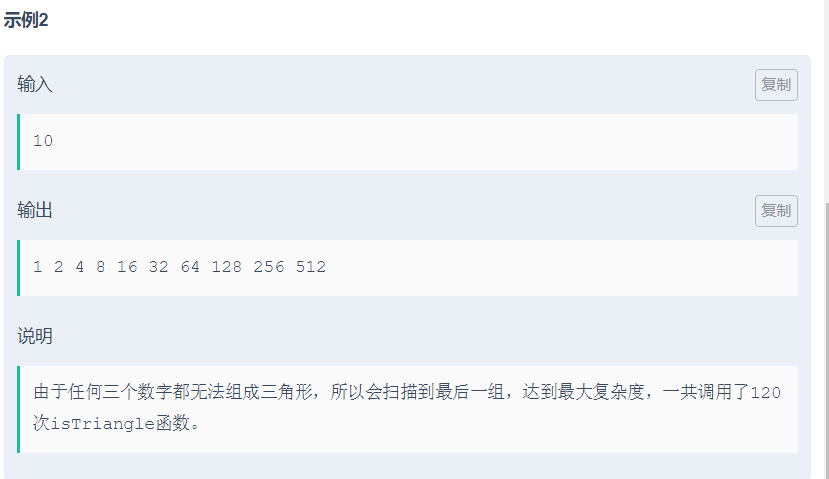
赛后才知道自己在后面的思路是错误的。看题之后就想到了斐波，然后比较了一下，C（3，n）和n^2long(2,n)，当n=35的时候刚好后面的复杂度是小的， 所以直接写出35之前的斐波（全部都不是三角形）。

 超过35的时候，我想的是直接F(35)依次+1，但是错了只过88.9%。还有就是前面的斐波我是从1开始的，这是不行的，得从2开始。毕竟斐波后面就全部都输出1。（就是开头的1那里想歪了）（在斐波那契段放弃使用1这个数字，这样非斐波段可以全部铺1铺满。）下面这个代码是从我的WA里面改写过来的AC，看了其他AC者的代码。

先k，再j，再i，所以起码要先i=1，j=1时，走一遍k，再j++，继续走，所以前面的数很关键，尽量不是三角形，后面的都是1才行

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;
ll aa[100008];
int t, n;
int main() {
    
    cin >> n;
    
    aa[1] = 2;
    aa[2] = 3;
    cout << 2 << " " << 3<<" ";

    if (n <= 35) {
        for (int i = 3; i <= n; i++) {
            aa[i] = aa[i - 1] + aa[i - 2];
            cout << aa[i]<<" ";
        }
        cout << endl;
    }
    else {
        for (int i = 3; i <= 35; i++) {
            aa[i] = aa[i - 1] + aa[i - 2];
            cout << aa[i] << " ";
        }
        int pp = aa[35];
        for (int i = 1; i <= n-35; i++) { 
            cout << 1 << " ";
        }
        cout << endl;
    }
}

还有另外一种逆序的写法，等待讲解。这样的简直起飞。

#include<bits/stdc++.h>
using namespace std;
int main(void){
    int i,n,x=1e9;
    scanf("%d",&n);
    for(i=1;i<=n;i++){
        printf("%d ",x);
        if(x>1) x=x/2;
    }
}

 

 

三、I题（线性筛+质因子特殊和）

https://ac.nowcoder.com/acm/contest/9982/I

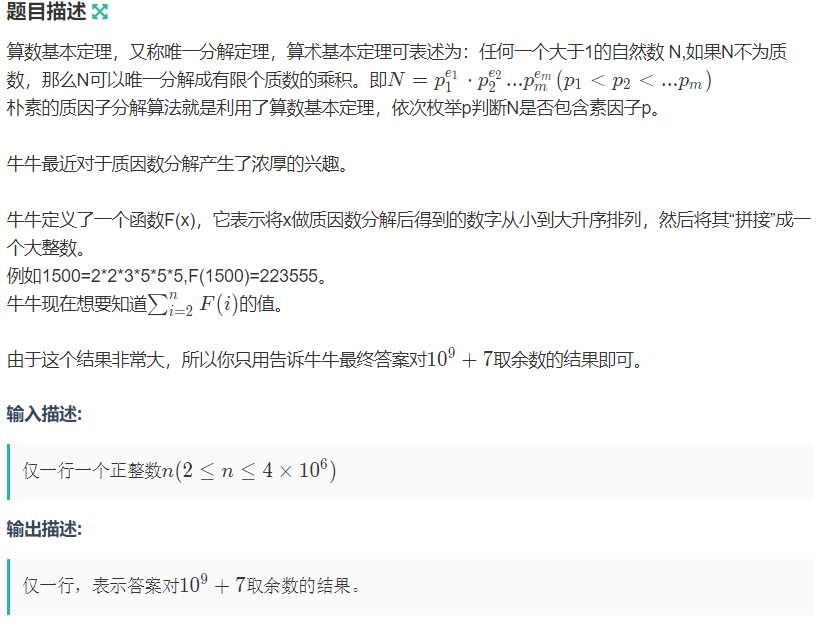
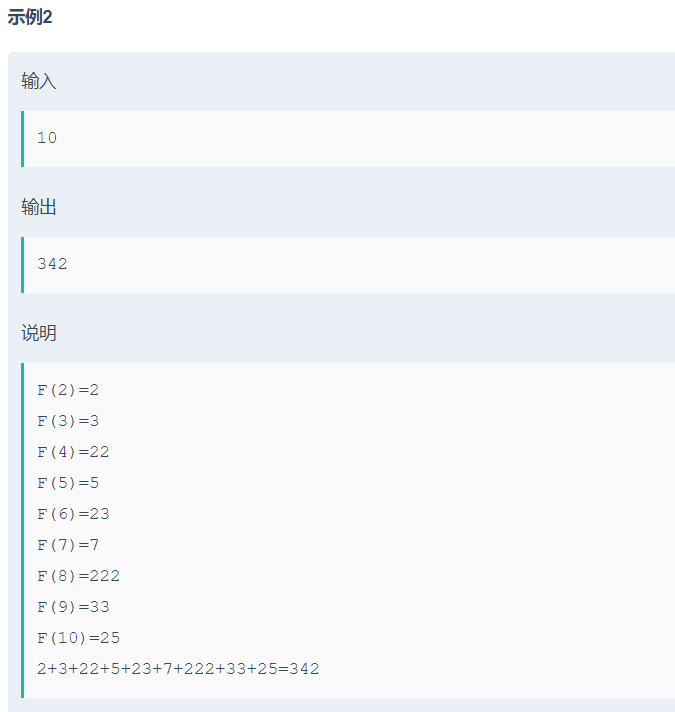
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
const int maxn = 4e6 + 7;
bool vis[maxn];
int prime[maxn], cnt = 0;
const int mod = 1e9 + 7;

void init() {//线性筛
    int m = maxn - 7;
    vis[1] = 0;
    for (int i = 2; i <= m; i++) {
        if (!vis[i])prime[ cnt++] = i;
        for (int j = 0, len = m / i; prime[j] <= len; j++) {
            vis[i * prime[j]] = true;
            if (i * prime[j] == 0)break;
        }
    }
}
int n;
int main() {
    init();
    cin >> n;
    ll res = 0;
    for (int i = 2; i <= n; i++) {
        int tmp = i;
        ll ans = 0;
        for (int j = 0; j < cnt; j++) {
            while (tmp % prime[j] == 0) {
                int temp = prime[j];
                while (temp)ans = (ans * 10) % mod, temp /= 10;
                ans = (ans + prime[j]) % mod;
                tmp /= prime[j];
            }
            if (tmp == 1)break;
            if (!vis[tmp]) {
                int temp = tmp;
                while (temp)ans = (ans * 10) % mod, temp /= 10;
                ans = (ans + tmp) % mod;
                tmp /= temp;
                break;
            }
        }
        res = (res + ans) % mod;
    }
    cout << res << endl;
}

 

 

四、D题（整块划分）

https://ac.nowcoder.com/acm/contest/9982/D

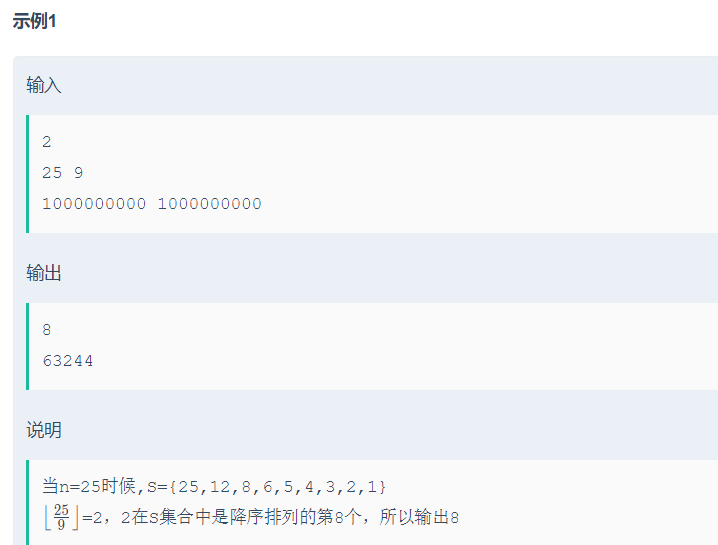
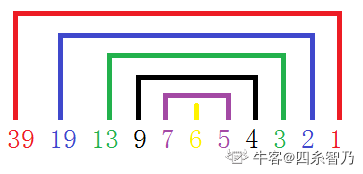
 这一题非常卡时间，只能O（n）才行，而且所有的cin与cout全部要换掉才行。

先看平方根开始两边扩开，但是需要注意一个点，就是假如n=42时，x=42是第12个，不是11，是因为7*6=42，所以6是与7搭配了的，所以后面要在判断一下

可惜了。

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
int t, n, x;
int main() {
    cin >> t;
    while (t--) {
        cin >> n >> x;
        int p = sqrt(n);
        if (x <= p)cout << x << endl;
        else {
            int y = p + (p - n / x);
            if (n / (p + 1) == p)y++;
            cout << y << endl;
        }
    }
    return 0;
}