背包基础
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define pub(n) push_back(n)
#define pob(n) pop_back(n)
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define PII pair<int,int>
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N = 110,mod=1e9+7;
int n,m;
int v[N][N],w[N][N],s[N];
int f[N];
int main()
{
ios;
sf(n),sf(m);
rep(i,1,n)
{
sf(s[i]);
rep(j,0,s[i]-1)
{
sf(v[i][j]),sf(w[i][j]);
}
}
rep(i,1,n)
{
pre(j,m,0)
{
rep(k,0,s[i])
{
if(j>=v[i][k])
{
f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
}
pf(f[m]);
return 0;
}
应我家小哥哥要求,将基础的动态规划写上,有一说一,写博客比敲这个代码时间还长
背包问题
01背包要点:1、物品多个,没有种类之分
2、一般思维就是选与不选的区别
3、优化做法就是由题目要求递推------------这里是由最大找最大-------------有时候也是可以由最小找最小
补充一下第三点:若要硬生生的追求优化之前和优化之后的联系,就是对优化之前的代码求同存异,找不同罢了,但是我一般喜欢理解成大大大,小小小(小鲤鱼,hh)

#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = b ; i >= a ; i --)
#define ll long long
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
typedef pair<int,int> PII ;
const int N = 1010,mod=1e9+7;
int v[N],w[N];
int f[N][N];
int n,m; // n==count m==V
int main(int argc,int *argv)
{
ios;
sf(n),sf(m);
//want to get max(w) init f to zero
rep(i,1,n) sf(v[i]),sf(w[i]);
rep(i,1,n)
{
rep(j,1,m)
{
f[i][j]=f[i-1][j];//not select i_th
if(j>=v[i])//select i_th
f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
pf(f[n][m]);
return 0 ;
}
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
typedef pair<int,int> PII ;
const int N = 1010,mod=1e9+7;
int v[N],w[N];
int f[N];
int n,m; // n==count m==V
int main(int argc,int *argv)
{
ios;
sf(n),sf(m);
//want to get max(w) init f to zero
rep(i,1,n) sf(v[i]),sf(w[i]);
rep(i,1,n)
{
pre(j,m,v[i])
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
pf(f[m]);
return 0 ;
}
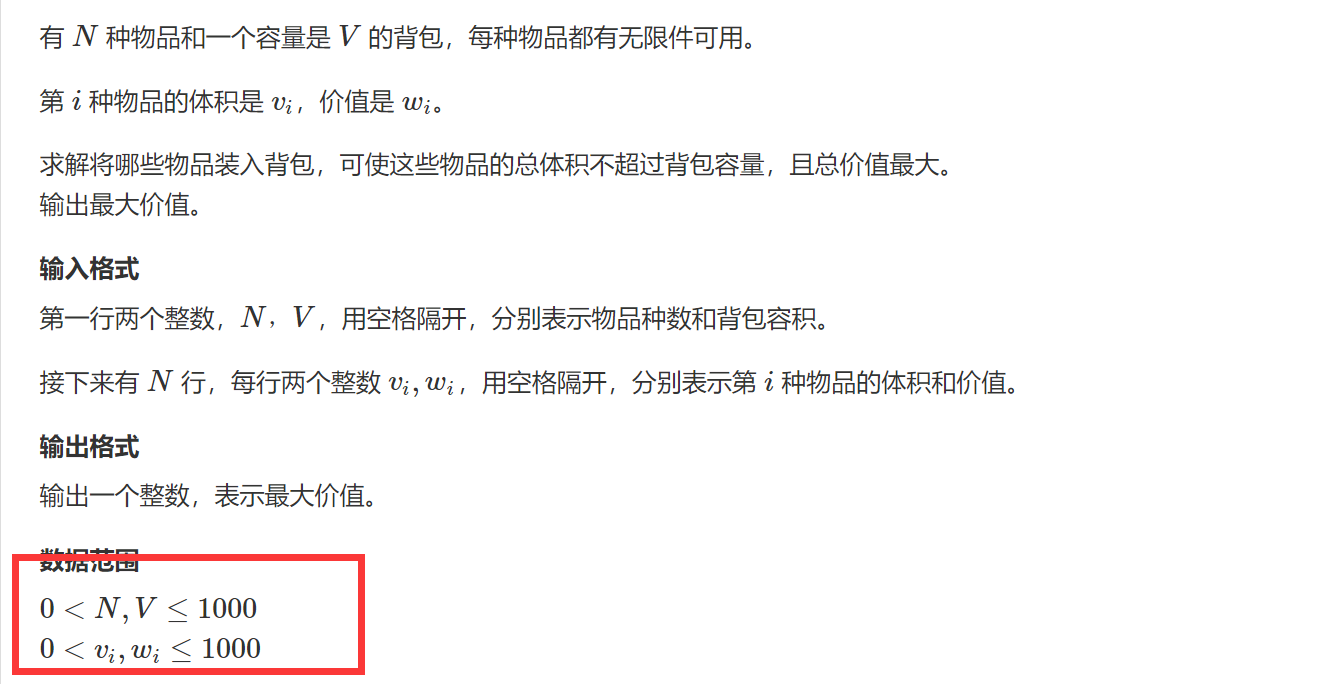
完全背包要点:1、除了种类不同之外,还有数量上的无限了
2、其实就是多了一个rep(k,,)的一个循环,让这个数尽可能的装下本种类的最多,然后又跟之前一样,有_i_的循环,可以选出最大值
3、多重背包这里需要进行牢记一下,优化过后是从小到大的,从大到小我尝试写过吗,但是发现错了
第一行去做的话
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
typedef pair<int,int> PII ;
const int N = 1010,mod=1e9+7;
int n,m; // n==species m==V
int v[N],w[N];
int f[N];
int main()
{
ios;
sf(n),sf(m);
rep(i,1,n) sf(v[i]),sf(w[i]);
/*firstly, we know complete dp dating to 01 dp
so,we can transform 2D to 1D-----f[]
*/
rep(i,1,n)
{
rep(j,v[i],m)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
pf(f[m]);
return 0;
}

多重背包理解一:1、就是在完全背包上的数量上被限制了
2、做法没有丝毫改变甚至有点想笑--------暴力解法
3、优化做法,按道理还是对空间进行优化----------具体理解到时候我打电话给你,这里面是有一个递推的过程的,他的优化先试经过滑动窗口,然后发现与f的第一位属性关系不大
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
typedef pair<int,int> PII ;
const int N = 110,mod=1e9+7;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main()
{
ios;
sf(n),sf(m);
rep(i,1,n) sf(v[i]),sf(w[i]),sf(s[i]);
rep(i,1,n)
{
rep(j,1,m)
{
for(int k=0;k*v[i]<=j && k <= s[i];k++)
{
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
pf(f[n][m]);
return 0;
}
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
typedef pair<int,int> PII ;
const int N = 110,mod=1e9+7;
int n,m;
int v[N],w[N],s[N];
int f[N];
int main()
{
ios;
sf(n),sf(m);
rep(i,1,n) sf(v[i]),sf(w[i]),sf(s[i]);
rep(i,1,n)
{
pre(j,m,0)
{
for(int k=1;k<=s[i] && k*v[i]<=j;k++)
{
f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
}
}
}
pf(f[m]);
return 0;
}

多重背包二理解:1、二进制优化,这个是模板提的二进制优化(有不理解的看官可以留言,不想写太多字,累了,写博客比敲代码时间还长)
其实就是对货物进行了打包,比如1024通常是要枚举1024次,但是二进制下只需要枚举10次了,降维打击
2、碰到的概率很低,因为,很少单独出一个多重背包,然后叫你优化一下
3、还是得强调一下,多重背包是有种类,有数量上的限制
4、上面的“陌生人”了是qq音乐的歌词,随机的,咋也不知道
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define pub(n) push_back(n)
#define pob(n) pop_back(n)
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define PII pair<int,int>
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N = 10100,mod=1e9+7;
int n,m;
int v[N],w[N];
int f[N];
int main()
{
ios;
sf(n),sf(m);
int cnt=1;
rep(i,1,n)
{
int a,b,s;
sf(a),sf(b),sf(s);
int k=1;
while(k<=s)
{
v[cnt]=a*k;
w[cnt]=b*k;
s-=k;
k*=2;
cnt++;
}
if(s>0) v[cnt]=s*a,w[cnt]=s*b,cnt++;
}
rep(i,1,cnt)
{
pre(j,m,v[i])
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
pf(f[m]);
return 0;
}

分组背包理解:1、已知种类,数量,但是没种选择的数量有限制
2、不优化的话直接按照思维走就好了
3、 优化的话也是按照01背包的方式进行优化
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define pub(n) push_back(n)
#define pob(n) pop_back(n)
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d\n",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld\n",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define PII pair<int,int>
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N = 110,mod=1e9+7;
int n,m;
int v[N][N],w[N][N],s[N];
int f[N][N];
int main()
{
ios;
sf(n),sf(m);
rep(i,1,n)
{
sf(s[i]);
rep(j,0,s[i]-1)
{
sf(v[i][j]),sf(w[i][j]);
}
}
rep(i,1,n)
{
pre(j,m,0)
{
f[i][j]=f[i-1][j];
rep(k,0,s[i])
{
if(j>=v[i][k])
{
f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
}
}
}
}
pf(f[n][m]);
return 0;
}
这里只是单个的总结,你先慢慢看吧,之后再把所有的背包联系起来,一些细节部分。有点困了
线性DP
区间DP
计数类DP
数位统计DP
状态压缩DP
树形DP
记忆化搜索


 浙公网安备 33010602011771号
浙公网安备 33010602011771号