区间选点-贪心-acwing

1、微扰：任何局部最优的微笑改变都会造成整体结果变差

2、范围缩放：任何对局部最优策略作用和范围的扩展都不会造成整体结果变差

3、决策包容性：局部最优策略提供的可能性包含其他所有策略提供的可能性

4、反证法

5、数学归纳法

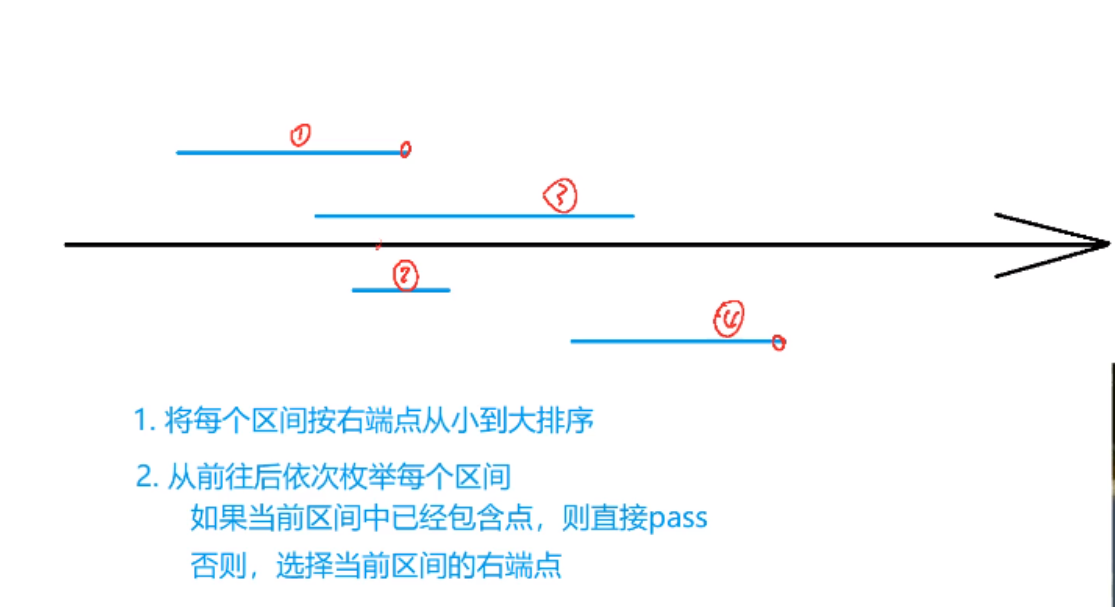
这道题目要求在数轴选点，使每个区间至少包含一个点，本质上是说，相交的区间选一点即可，不相交区间须选二点，其实也就是找到最大不相交区间数量
但是以我的理解就是求出的最小区间ans一定小于等于所有符合条件的可能的数量ans<=cnt

然后又因为在尽可能避免区间不想交的情况下ans>=cnt

思考：正确解释应该是可以对区间的端点进行排序，之后安排排序后的大小来查看当前需要抉择的区间是否有不想交或者或者已经有点的存在了

 

#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = b ; i >= a ; i --)
#define ll long long
#define inf 0x3f3f3f3f
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
typedef pair<int,int> PII ;
const int N=2e6+10,mod=998244353,p=233;

int n;
struct Range
{
    int l,r;
    bool operator< (const Range &w) const
    {
        return r<w.r;
    }
}range[N];

int main()
{
    ios;
    cin>>n;
    rep(i,0,n-1)
    {
        int l,r;
        cin>>l>>r;
        range[i]={l,r};
    }
    sort(range,range+n);

    int res=0,ed=-inf;
    rep(i,0,n-1)
    {
        if(range[i].l>ed)
        {
            res++;
            ed=range[i].r;
        }
    }
    cout<<res<<endl;
    return 0;
}