强迫风冷散热
风机的选型
具体的要求:
- 在给定条件下确定风量、风压以及抽风风机的适用范围、风扇噪声的考量;
- 通过经验公式估算风扇风量,进行风扇选型;
- 常用的有强迫风冷散热、TEC(Thermoelectric Cooler)热电冷却器(帕尔贴 Peltier 效应)。
1. 风机的分类
轴流风扇(Axial Fan)和离心风扇(Centrifugal Fan)两类。
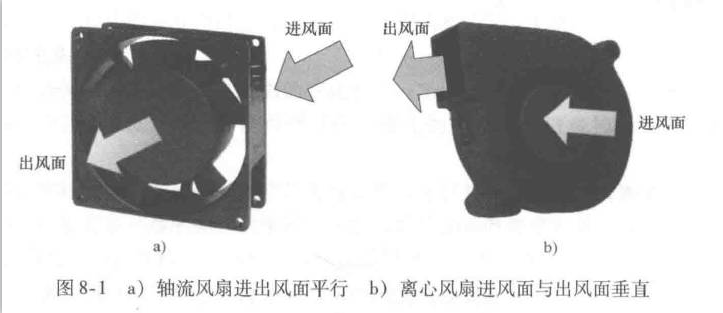
两者主要的区别除了外形上的区别外:
- 轴流风扇:风压小,风量大,适用于风阻小,风量要求大的系统;
- 离心风扇:风压大,风量小,适用于风阻大,风量要求小的系统(比如笔记本散热系统,由于出风口处的散热鳍片较密风阻较大,因此要选用离心风扇进行散热)。
选用风扇时要考虑的因素主要有:
- 风扇尺寸;
- 风量需求;
- 系统阻力以及风扇所需要的风压;
- 风扇转速控制方式;
- 噪声;
- 使用环境以及机器使用寿命;
- 成本。
2. 风扇的风量
定义:单位时间内流过系统的气体体积,同时也是表征风扇对空气的扰动强度。
单位:\(m^3/s\)
这里注意是流过 系统 的气体体积,而非流经风扇本身前后出风口的流量。
风量的确定依据是热力学第一定律——能量守恒定律,因此有估算公式,前提条件是:系统设备内部的散热量(kW)以及允许的最大温升(℃) 两者已知:
这里的空气物理性质根据不同的温度值来确定,如下表可参考该表为一个标注大气压下的数据,如果考虑海拔高度时,需要带入海平面空气的比热与密度的变化属性:
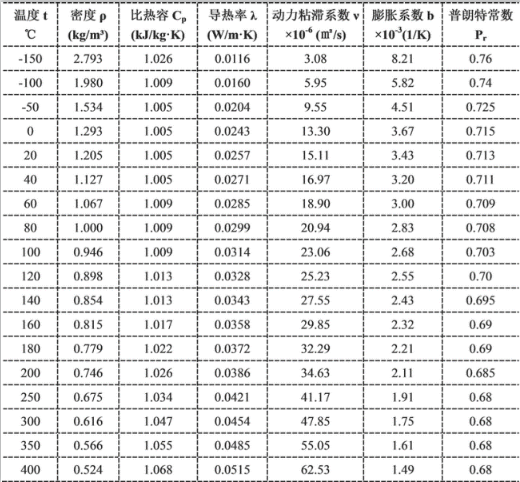
通过公式(1)得到的风量单位为\(m^3/s\),常用的单位还有 \(m^3/min\) 和 CFM,如果上面的功率单位为\(W\),则公式(1)需改成:
- 转换成 \(m^3/min\) 时,公式(2)变成:\(Q = \frac{60P}{1000\Delta T \rho C_p}\);
- 转换成\(CFM\)时,公式(2)变成:\(Q = \frac{2118.88P}{1000\Delta T \rho C_p}\)。
1 CFM = 1\(ft^3/min\):立方英尺每分钟,换算成\(m^3/s\) --> \(1m^3/s = 2118.88 \; CFM\).
1\(atm\)=\(101325 \, Pa\)=\(760mm \, Hg\)=\(10332.27mm \, H_2O\),1mm水柱\(\approx9.80665Pa\)
比如某风扇的规格参数:风压P=1.53mm水柱;最大风量Q=66.17CFM;转速R=1500 rpm;那么有:风压P=\(\frac{1.53}{10332.27} \times 101325 = 15.01Pa\);风量Q=\(\frac{66.17}{2118.88}\)=0.03123\(m^3/s\).
进一步就有:这里选择常温20℃时的标况,\(C_p = 1.005 ,\rho = 1.205kg/m^3\),风量单位为CFM时
由于系统阻力的存在,风扇的实际风量值要小于上面计算的值,上面计算的值是风扇产品的工作点对应的风量,并不是指满足系统散热要求的最大风量。在风扇进行选型时,风扇最大风量可按照1.5 ~ 2倍的计算值来选择。
风量初步确定之后,初选风扇之后,假设风扇框直径\(D_2\),Hub轴直径\(D_1\),计算通流面积,进一步得到无遮挡侧风速为:
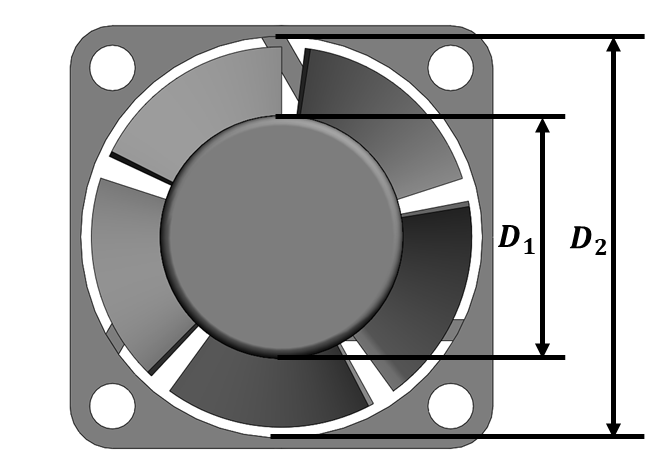
通风孔侧风速需要从噪音的角度考虑,对于室内产品来讲,一般风速低于5m/s最好,因此通风孔侧通流面积可以初选:\(A = \frac{Q}{5}\).
风量确定了,风压怎么确定呢?首先使用的风压大小取决于系统阻力,因此需要计算系统风阻,但是风阻计算比较复杂,因此一般的做法就是增加风量余量,因为系统散热能力主要由风量决定。
那么就有一种可行的方法,前提是能看出风扇工作点的风压和风量大小,即根据风量选择风扇,然后通过实际仿真确定工作点,进一步调整。如图,判断工作点的位置是否位于工作点区域即可:
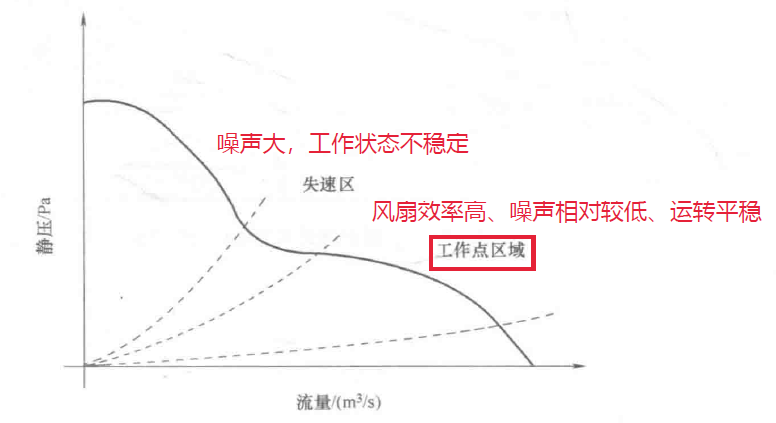
查看风机工作点的方法:由于风机的工作点仅与系统阻力有关,因此可以先进行不考虑热源的情况下进行仿真,通过获取流过风机的流量值,进一步与P-Q曲线对比判断工作点所处的位置。
如果风机工作点出于高风压、低风量区域,此时说明系统阻力过大,可以通过改变零件布局的方式来降低系统阻力,如果系统布局已经固定,那么可以降低风机风量,使工作点出于高效区域。
系统实际获得的风量是系统的阻抗曲线与风机\(PQ\)线的交点所对应的风量,其中\(P\)是指压力,\(Q\)指风量,均为标准国际单位。

通过上图可知,B点为该风扇在该系统中的实际工作点,并可以得知该风扇在该系统中工作时实际的风压与风量。
Note:P-Q曲线中,凹陷明显的位置处通常是风扇的失速区。失速区产生的主要原因是系统阻抗过高时,出风口静压增大,而进风口进气不足,扇叶进风面附近空气流速减小,在高静压作用下,气流边界层被破坏,叶片尾端出现涡流区,导致空气可能直接脱离叶面而导致扇叶振荡,产生噪音,这就是所谓的失速现象,在P-Q曲线上的表现就是凹陷区域。
因此避免风扇失速,风扇出风口处不要与零件距离太近。
3. 风扇的风压
风压一般指静压,为风扇出、入风口观测压力之差
Icepak中定义:\(P_{fs}=P_{discharge}-P_{intake}\), where \(P_{intake}\) is the pressure averaged over the face of the intake side of the fan, and \(P_{discharge}\) is the pressure averaged over the face of the discharge side of the fan.
-
对于机箱 Internal 内部的风扇,\(P_{discharge}\)和\(P_{intake}\) Icepak 会自动计算各自的值;
-
对于Intake(吹风)类型的风扇\(P_{discharge}\) 软件自动计算,\(P_{intake}\) 为外部环境压力,因为是自外部向系统内部送风,因此需要在
Basic parameters-->Ambient conditions中设置外部环境压力; -
对于Exhaust(抽风)类型的风扇,\(P_{discharge}\)为外部环境压力,\(P_{intake}\) 由软件自动计算得到。
外部环境压力默认为0,该压力值表示表压
确定风扇的风压首先需要确定系统的阻抗曲线,系统阻抗曲线最准确的获得方法时风洞测试,但是很难具备测试条件。一般通过仿真来获取,通常直接根据尺寸初选风扇进行仿真,结合仿真所得压力损失来得带选定合适的风扇。
对于风扇性能不足的情况可以采用串、并联风扇提高性能。
-
风扇的串并联等效PQ曲线
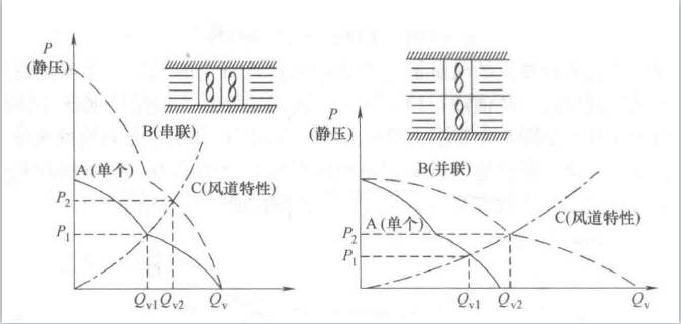
- 风扇串联:适用于高阻抗系统;
- 风扇并联:适用于低阻抗系统。
串联时在两风扇之间增加整流装置后,在零风量条件下静压甚至可以达到 \(1+1>2\) 的效果!
并联时由于两风扇之间会出现流场干扰,因此实际并联后的总风量小于两风量相加。
4.散热器
4.1 散热器设计原则
散热形式有自然冷却、强迫风冷、水冷、微通道、浸没式散热等形式,散热离不开散热器的结构。
散热器基板的厚度参数是影响散热器效率的重要因素之一。散热器基板较薄时,向远离热源肋片传递的热阻较大,会导致散热器上温度分布不均匀,且抗热冲击能力较弱。
增加基板厚度可以改善温度分布不均匀的问题,并且能提高抗热冲击能力,但是物极必反,基板过厚时,不仅仅会增加自重,主要的问题是会造成热量的累积,进而降低散热能力。
良好的基板厚度设计应该是热源部分厚,远离热源薄的结构,可以达到吸收足够多的热并向周围较薄的部分迅速传递。
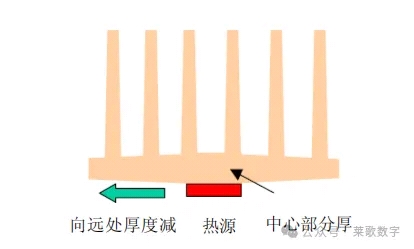
散热器中影响散热的参数有:散热器齿间距、厚度、高度。其也是确定散热器肋片数量、分布以及散热器展开面积的重要参数。
在散热的过程中,与流动方向相同的表面积散热效率高,与流动方向垂直的表面积附近的流体存在静止和漩涡流体,这部分表面积无法带走太多热量。
对于依靠自然对流散热的情况,依据小拇指原则:散热器鳍片之间可以容纳小拇指,或者肋片间距须在4mm以上才能保证自然对流顺利。这是因为对流散热的驱动力是温差,肋片附近的边界层厚度可达2mm,因此需要保证4mm以上的间距最好。
对于强迫风冷散热,翅片间的高速流动压缩边界层,较自然对流情况下小很多,那么此时翅片间的距离可以取4mm以下,但是受到加工手段、动力元件驱动的影响,也不能做的过小。
此外,翅片的高度和厚度的平衡也很重要,以某自然对流散热设计交换机的散热体积估算为例:

首先须知散热器的包络体积:散热器所占的体积,如上图所示。
定性的来讲,发热功率大,散热器的包络体积越大,定量的来讲,可以使用下面的经验公式来计算
式中:\(V\)为包络体积,单位为\(cm^3\),最小为1.5;Q为解热能力,单位为\(W\)。
在实际的加工过程中中间厚边缘薄的散热器很少见,一般都是均厚加工,基板厚度与散热器解热能力之间的关系式为
式中,\(t\)为基板厚度,单位\(mm\),最小厚度为2;\(Q\)为解热能力,单位为\(W\)。
对于自然对流问题,基板厚度为\(T\),翅片厚度为\(t\),翅片高度为\(h\),参考值如下表
| T(mm) | 2~4 | 4~6 | 6~8 | 8~10 | ≥10 |
|---|---|---|---|---|---|
| t(mm) | 1.5 | 2 | 2.5 | 3 | 4 |
| h(mm) | ≥6 | ≥8 | ≥8 | ≥10 | ≥10 |
为避免影响肋表面的对流,一般情况下,齿间距大于6mm。如果散热器肋高低于10mm,可以按照齿间距不小于1.2倍齿高来确定散热器的齿间距。
对于强迫散热,可以根据流过其空气的流速来调整齿间距,下表为空速与流向长度之间的关系
| 空气流速 | 75mm | 150mm | 225mm | 300mm |
|---|---|---|---|---|
| 1.0 m/s | 4 | 5 | 6 | 7 |
| 2.5 m/s | 2.5 | 3.3 | 4 | 5 |
| 5.0 m/s | 2 | 2.5 | 3 | 3.5 |
有了初步的尺寸之后,可以根据软件进行仿真来进一步优化散热器设计。
4.2 平行翅片散热器流阻计算
强迫风冷设计中的大部分散热器和液冷设计中的冷板中都会存在阵列式翅片结构,选择风扇时,除了要考虑流体流量,还要考虑相应流量下的流动阻力。
流动阻力产生的主要原因有:
- 实际的流体都具有黏性,在流经物面时,紧贴物面的流体质点会黏附在物面上,这些流体质点与物面之间的相对速度为0,但实际的流体流动速度并不为0,因此在物面附近会存在流动梯度,根据牛顿内摩擦定律可知,存在速度梯度的流体必定会存在流动阻力;
- 流体流经障碍物时,会遇到凸起表面等由此产生流体分离,进而产生倒流,会出现漩涡,漩涡的形成和存在会产生附加阻力;
流经散热器产生的流阻宏观体现在散热器两侧的压强差上,流动阻力的计算基于以下假设:
- 不考虑由于温度差导致的空气密度差;
- 散热器的各个翅片相互平行;
- 流态为发展充分的层流,对于平行平板间的流动,最小临界雷诺数通常被认为是1300,且适用于绝大多数散热器的工作状态。
典型的阵列翅片散热器以及对应参数如下图:
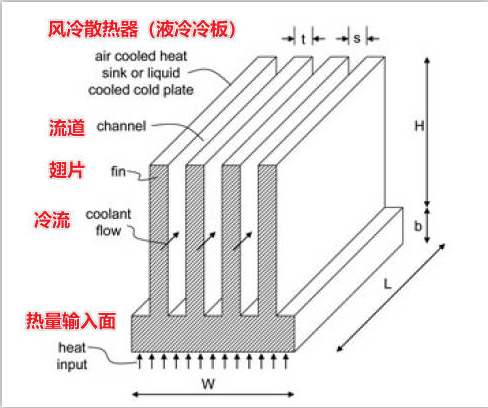
coolant flow: air or liquid
流动阻力的计算根据是否考虑出入口效应来展开。出入口效应是指,流体从开放区域进入散热器区域时,流体会突然收缩;当流体从散热器区域进入开放区域时,流体会突然扩张,流动空间的突变将会导致流速突变进而形成不同的速度梯度,诱发漩涡,漩涡进而会消耗能量。
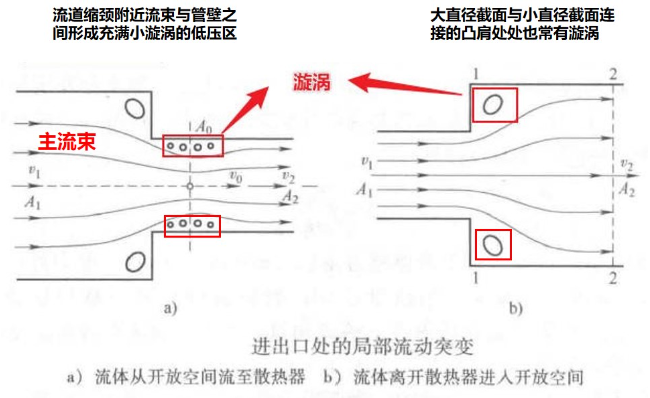
(1)不考虑出入口效应
此时阻力产生的主要原因是流体粘性所产生的内摩擦力,表征流动阻力的物理量为压降,压降使用范宁公式(Fanning Formula)计算:
其中:\(f:摩擦阻力系数;D_h:水力直径(特征尺寸);L:翅片长度;\rho:流体密度;u:流体流速\)。在流量已知,散热器参数已知时,未知量只有\(f\),在无限大平行平板层流流动时,摩擦阻力系数可以按照下式进行计算:
将式(4)带入式(3)就有:
特征尺寸\(D_h\)计算方法为:
特征长度/水力直径\(D_h\)的计算:\(D_h=4\frac{A}{C}\);式中,A为截面积;C为湿周,即流体与固体边界接触部分的周长。
在翅片高度H>>翅片间距S时,特征尺寸\(D_h \approx 2S\)。
(2)考虑出入口效应
其中:\(K_c和K_e分别为入口和出口的压降效应参数;f_{app}为表观摩擦系数\):
其中\(N_f\)为翅片数目。
这些仅仅是简化计算,实际的流动要更复杂,与流体接触的所有固体均会产生诱发流阻。单凭经验公式计算得到的流阻与实际的误差还是很大的,流阻无法确定,那么风扇的工作点也不确定,风扇的流速也无法确定。因此在实际的应用中,最常用的方法就是,首先假定一个流速,推算其流阻,然后校核此流阻与风扇在此工作风量下的风压是否匹配,如果不匹配重新假设流速,直至符合。
5. 风扇的抽风与吹风设计
| 设计风向 | 系统腔室压力属性 | 风扇入口侧热环境 | 风扇风口在系统侧流态 | 使用场景 | 注意事项 |
|---|---|---|---|---|---|
| 抽风设计 | 负压 | 入口高温 | 层流 | 使用热源比较分散的场景,结构紧凑、阻力较大的产品也适合 | 系统内部处于负压,因此会导致灰尘等小颗粒进入系统 |
| 吹风设计 | 正压 | 入口低温 | 湍流 | 适用于热量集中的产品 | 风扇出风口附近、Hub轴附近存在流动死区,高热风险器件避免在该位置;建议障碍物与风扇前缘隔开至少一个风扇厚度的距离;吹风设计时,目标出风口之外的开孔对散热是不利的 |
6. 风扇的转速控制
对风扇进行调速的目的在于在保证系统散热要求的前提下,降低风扇工作产生的噪声。风扇主要分为两线风扇、三线风扇和四线风扇。
- 两线风扇:两根线为正负极,无任何信号反馈,因此无法读取转速,只能通过调节电压来控制转速;
- 三线风扇:正负极加信号输出线,可以读取转速,但仍基于电压调速,控制精度与两线风扇相当;
- 四线风扇:正负极加信号输入输出线,通过PWM脉冲信号调节占空比来控制转速,控制精度要优于上述两者。
风扇调速的依据是系统的温度,因此需要温度传感器获取实时的温度,温度传感器对风扇调速的调整基准参考性顺序为:芯片内置温度传感器 > 板载温度传感器 > 可拔插式温度传感器 > 风扇内置温度传感器。
1)芯片内置温度传感器:选择热风险最高的芯片的温度传感器示值作为风扇调速依据,比如CPU散热风扇的调速依据就是CPU的核心温度,GPU散热风扇的调速依据就是GPU核心温度。
2)板载环境温度传感器:靠近设备入风口处,即受其他器件温度影响较小的位置。
3)板载芯片温度传感器:用于及时间接反应芯片的温度,置于芯片下风口处,距离5mm位置最佳。
4)可拔插式温度传感器:感温点置于风速大、不受其他器件影响的位置,最能反馈局部空气温度的位置。
(1)风扇转速与噪声的经验公式
其中:\(SPL(Sound \: Pressure \: Level)为声压级噪声;RPM(Round \: Per \: Minute)为风扇转速,RPM0表示最大转速\);\(K\)为经验参数,不同产品该参数各异,常用的风扇一般该值在50 ~ 60之间,常用55来进行评估。
(2)风扇转速控制方式
| 控制方式 | 操作方式 | |
|---|---|---|
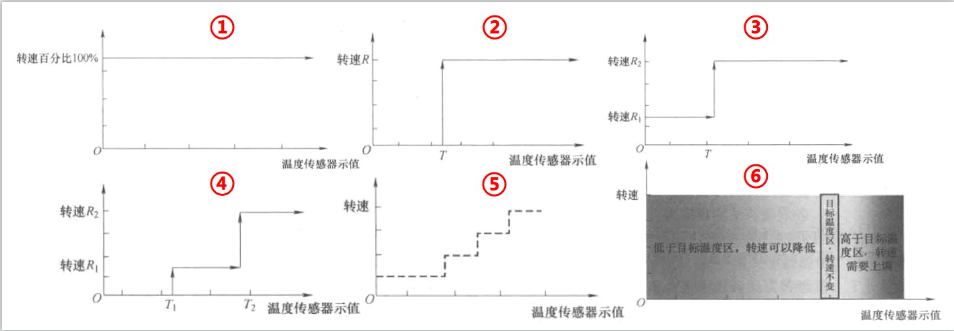
| ① | 全速 | 不做任何控制 |
| ② | 设置开、关两种状态 | 首先需要设定一个参考温度\(T_0\):如果实际温度\(T>T_0\),风扇按照预定转速运行;如果\(T<T_0\),风扇不运行 |
| ③ | 设置两种风速状态 | 参考温度\(T_0\),如果实际温度\(T<T_0\),以转速\(R_1\)运行;如果实际温度\(T>T_0\),以转速\(R_2\)运行 |
| ④ | 设置三种风速状态 | 实际温度\(T<T_0\),风扇不运行;如果\(T \in [T_0,T_1]\),风扇以转速\(R_1\)运行;如果\(T>T_1\),风扇以转速\(R_2\)运行 |
| ⑤ | 设置N种状态,划分多个温度区间 | 与上面类似,对于运行环境较为稳定的产品(服务器、大型通信设备等),施加一定负载,转速与最高温度呈稳定关系 |
| ⑥ | 以达到目标温度调节转速(目标控速) | 设置目标温度为一个范围,而不是一个准确的值,这是因为风扇转速的调节与对温度的作用效果之间存在一个延迟 |
(3)风扇调速策略整定
上面的控速方法中①~⑤均为转速与温度一一对应的关系,方法⑥则不是一一对应的关系。控速方案的设计主要包括以下步骤:
-
首先需要确定温控策略:是以芯片温度为参考还是以环境温度为参考;比如对于CPU、机箱电源以及GPU散热,显然是基于芯片温度进行调速的,因为温度过高会导致电脑无法正常运行或者严重影响电脑性能。而对于机箱外部辅助散热风扇则是基于板载温度传感器的温度来进行调速的,只需要负责机箱内部温度保持一定范围即可。
- 如果以环境温度为参考,测试在不同环境温度下,所能使环境温度降至要求温度时的风速和此时温度传感器的示数,作为算法的输入依据;
- 如果以芯片温度为参考,根据产品在不同环境温度下的噪声要求,测试对应芯片的温度和风扇转速,作为算法输入依据。
-
协同软件工程师编写算法,最终仍需要做进一步的验证,不行就重新执行上述步骤。
7. 风扇模型在Icepak中的定义
7.1 轴流风扇
(1)几何属性定义
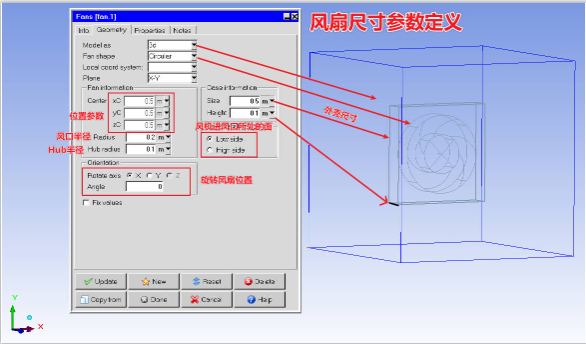
(2)风扇属性定义
① 风机PQ线
关于Fan flow属性中,分为线性、非线性和固定值,其中取固定值时,风扇必须放置在Cabinet(机箱)或者Hollow block(中空块)上,Intake 和 Exhaust 均可设置这三个参数,Inernal 类型的风扇不可设置固定值,只能是线性或者非线性PQ曲线。

-
线性:就相当于设置PQ曲线的两个典型点的值:(0,\(Q_{max}\))和(\(P_{max}\),0),即风量为0的时候风压的最大值、风压为0的时候风量的最大值,由此线性近似PQ线,根据这两点的坐标即可确定一条直线。
已知两点坐标可知直线方程:\(P = \frac{P_{max}-P}{P_0}Q_{max}\)
-
非线性:可以通过直接使用编辑表格的形式来定义PQ曲线坐标点,也可以直接通过点击点来确定坐标点。
在以文本形式定义坐标点时,注意风量 风压数值之间要以空格隔开;并且第一行和最后一行的数字必须为0,即必须输入风量为0时的最大风压、风压为0时最大风量。
② 风机转速(Swirl)
这里需要注意的是,如果设定了风扇在某一转速下的PQ曲线,那么这里就不用输入转速了。
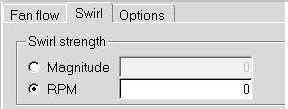
对于外部导入的CAD模型该参数不适用。
③ 其他Options
在实际的操作过程中,风扇在额定转速下的P-Q曲线是可以通过说明书获得的,但是如果换成其他转速时,风扇P-Q曲线该如何获得呢?
Icepak软件中可以自动获得,只需通过以下步骤进行正确设置:
-
设置额定转速下的P-Q曲线;
-
设定风扇的额定转速:
Swirl->RPM; -
在
Option中的Operating RPM中输入新的转速值,软件就会自动计算新转速下的P-Q曲线。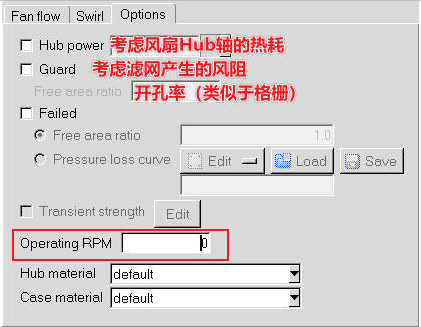
不同转速下的P-Q曲线计算方法:\(\frac{p_2}{p_1}=\frac{N_2^2}{N_1^2},\frac{Q_2}{Q_1}=\frac{N_2}{N_1}\)
④ 补充内容
第③节所用的原理就是风扇相似定理,风扇各项参数发生改变时,所存在的一些规律。
其中\(D\)为风扇直径;\(W\)为风扇功率;\(\rho\) 为流体介质密度。
第③节中,根据额定转速来确定新转速的的P-Q曲线时,曲线上的任意一点坐标值都可根据上式进行计算。同一风扇的风扇直径\(D\)相同,所以不同转速下的风量\(Q\)之比就是对应风速\(N\)之比。类似的,由于风扇位置没有发生改变,并且还是在原系统中,不考虑流体介质密度的变化,所以不同转速下的风压\(P\)之比就是对应风速\(N\)之比的平方。
对于同一系统、同一风扇就有 \(D、\rho\) 相同,假设\(N_1\)为额定转速,\(N_2\)为新定义的转速,那么式(8)就可改写成:
7.2 离心风扇
(1)离心风扇常见类型
如图所示为两种典型的风机模型示意图:
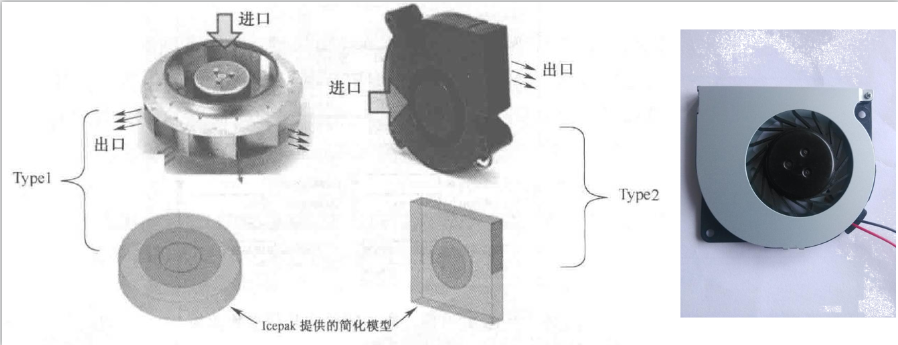
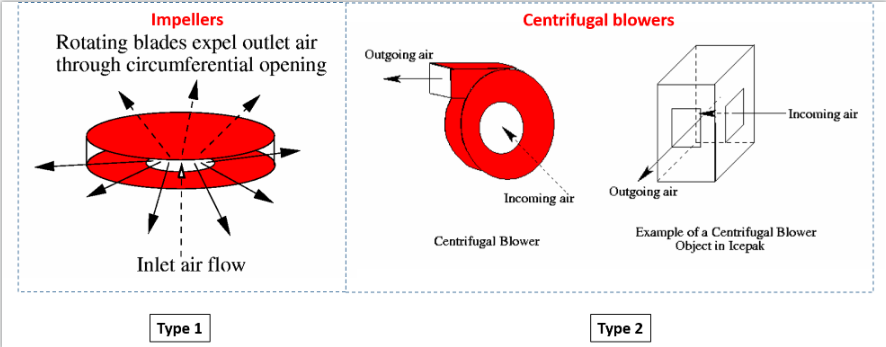
Icepak中的离心风扇就有上述两种类型:
- Type 1 的特点是风扇外形为圆柱状,并且出风口为圆柱的整个环形面;
- Type 2 由空心棱柱体、流体出口以及一个或者两个流体入口组成。
(2)离心风扇在Icepak中的属性
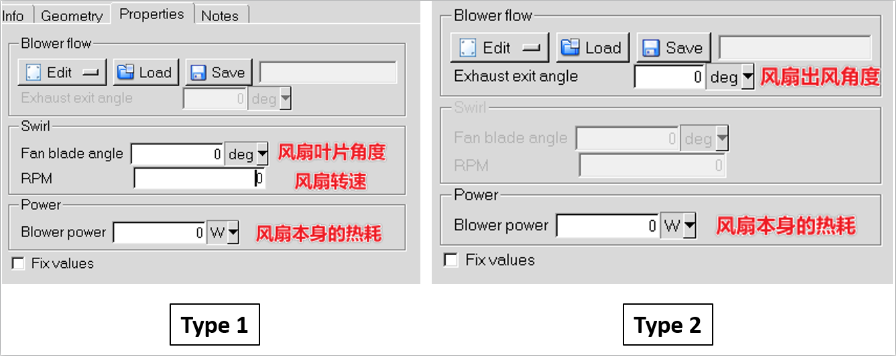
-
对于Type 1 中的 转速Swirl 设置,如果风扇按照顺时针旋转,那么RPM需指定为负值;如果按照逆时针方向旋转,RPM需指定为正值;
-
如果 Fan blade angle 不知道并指定为0值时,那么软件会默认为1弧度。
TEC热电冷却器
1. TEC原理简介
1.1 TEC工作原理
TEC工作原理发现于1834年,由Peltier发现,在不同材料的金属间施加直流电时,除产生焦耳热外,热量还会发生定向转移,即两种金属之间接触处出现温差,这就是热电冷却器工作原理,又称帕尔贴(Peltier)效应。本质原因是电子在不同材料的导体中具有不同的能级,电子进行能级跃迁时会带有能量的吸收和释放。由于半导体材料上的这种现象更加明显,热电冷却器大都是半导体冷却器,因半导体材料碲化铋具有优异的热电性能,是最常用的半导体材料。
常见热电冷却器是由多个P型和N型半导体材料结构件以电串联和热并联的方式组成。TEC的组成结构:基本元件是电偶,其由金属电桥链接两个电偶臂组成。金属电桥即导电层,铜质材料,一个电偶臂是P型半导体材料,另一个电偶臂是N型半导体材料。
- N型半导体:N即Negative,为了提高半导体的导电性,由本征半导体(不含杂质的纯度高的材料)中掺杂5价元素得到的半导体材料,由于硅原子之间通过共价键连接,其属于主族元素,主族元素的价电子为最外层电子,硅元素的价电子为4个,掺杂5价元素(磷或砷)后,形成共价键后仍会多出一个电子,因此对于N型半导体,电子的浓度要大于空穴,因此主要的载流子为电子;
- P型半导体:P即Positive,同理,向本征半导体材料中掺杂3价元素(硼或铝),价电子形成共价键的同时,有一个共价键会多出一个空穴,因此对于P型半导体,空穴的浓度要大于电子,因此主要的载流子为空穴,空穴是无法移动的。
如图所示电路中,在直流电的作用下,电子流经P型半导体时,电子与空穴复合,能级降低,因此释放能量;电子由P型半导体流入N型半导体时,能级跃升,因此需要吸收能量,这样就产生了冷端和热端。
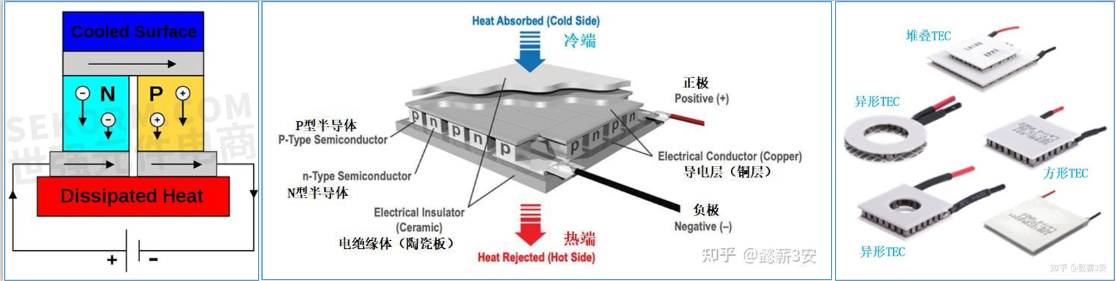
热电冷却器既能制热,又能制冷,制冷效率相对不高,制热效率很高永远大于1,通过改变电流方向即可实现制冷与制热的转换。
TEC可以理解成一个热泵,即用于输运热量的泵,其消耗的电能不是直接进行做功,而是用来“搬运”热量,\(Q_c\)值表示TEC制冷量,即TEC从冷端到热端的热量搬运量。制冷量计算公式:
其中\(\alpha\) 表示塞贝克系数(温差电动率系数)\(\alpha = \alpha_P - \alpha_N\),即与半导体材料本身有关,\(\pi = \alpha I\)称之为帕尔贴系数,\(I\)为工作电流,\(\Delta T\)为冷热面温差:\(\Delta T = T_h - T_c\),\(T_c\)为冷端温度,\(T_h\)为热端温度,\(R_{AC}\)为TEC内阻,\(K\)为冷热端之间的导热系数。因此可以通过适当增大电流、降低冷热端温差来提高制冷能力。那么在热端,就需要性能好的散热器使之与冷端的温差足够小,这样TEC的综合效率系数就会更大。
塞贝克效应:两种不同材料、不同温度的导体组成的回路中,接触点存在温度差\(\Delta T\),那么闭合回路中就会产生电流,同时导体两端会产生一个电动势\(\Delta U\),该电动势就是Seeback 电动势,这种效应就是塞贝克效应。
\[\Delta U = \alpha \Delta T \]可知,\(\Delta U\)正比于温差\(\Delta T\),且有温差不大时,\(\alpha\) 是一个常数,其由两种材料共同决定。
另外,由公式(10)可知,制冷量是电流的二次函数,且为开口向下的抛物线,因此存在一个电流值使得制冷量为最大值,通过求导计算的制冷量最大时:\(I=\frac{\alpha T_c}{R_{AC}}\),带入式(10)中,\(R_{AC}=\frac{\rho L}{A}\),\(K = \frac{kA}{L}\),最大制冷量与热电偶的横截面积成正比,与长度成反比,即横截面积额越大,长度越小时,越粗短的的电偶的制冷量越大;制冷系数与面长比无关,只于电阻率、导热系数和温差有关。
傅立叶效应:均匀介质中沿某个方向在单位时间内传到的热量。该热量的大小正比于该方向的温度梯度和垂直于该方向的面积的乘积:\(Q_k=\frac{kA}{L}\Delta T\),\(k\)表示导体热导率,\(K\)为总热导。
TEC的使用在小尺寸的电子产品中受限,因其制冷效率相对较低,导致整个系统的热耗增大,加重系统散热负担。因此在使用TEC时,要衡量保证局部低温的情况下,考虑整体系统的温升是否可以通过某些手段将其降至要求范围内。TEC由于热电效应,导致另一侧的温度急剧升高,使之与环境温度温差加大,热量传输动力更大,因此在某些情境下,加以引导,可能给电子产品的热设计带来创新空间。
热电冷却器的冷端接热源,热端一定要安装散热器,否则会烧坏热端材料!
1.2 理论推导
以图示回路为例,对TEC的原理进行理论解释:热结点温度\(T_H\),向外界释放的热量\(Q_H\);冷结点温度\(T_C\),从外界吸收的热量\(Q_C\);热电偶输入电压\(U\),输入电流\(I\),输入功率\(P=UI\)。

1.2.1 制冷量
根据热力学第一定律(能量守恒):热端释放的热量 = 冷端吸收的热量 + 热电偶输入功率
那么根据帕尔贴效应,吸收热量为冷端,释放热量为热端,吸收的热量称为帕尔贴热,则产生的帕尔贴热\(Q_P\)就有
理想情况下\(Q_P\)应该等于制冷量\(Q_C\),但是由于焦耳热和傅里叶效应的存在,实际的制冷量要小于帕尔贴热:\(Q_P = Q_C + Q_{Loss}\),假设外界对电偶不存在影响的情况下,将电偶视为一个横截面积为\(A\)、长度为\(L\)的长臂,导热系数为\(k\),电阻率为\(\rho\)时,根据焦耳定律和傅里叶效应在干长的方向进行积分得到
进一步就有实际的制冷量\(Q_C\)
TEC输入的功率包含内阻产生的热损耗和克服Seeback效应需要的功率,假设内阻为\(R\),克服塞贝克电动势\(\Delta U\),则输入功率\(P\)
则制冷系数(COP)为
如果使用TEC制热的话,制热系数为
这也就解释了为什么TEC制热效率大于1,要高于制冷效率。
1.2.2 最大制冷量
通过式(14)发现,制冷量是电流的二次函数,在冷端温度和温差不变时,帕尔贴热项正比于电流值,而焦耳热也正比于电流值,电流越大由内阻导致的热耗增大,因此存在最大值(抛物线开口向下),进一步对\(Q_C\)关于\(I\)求一阶导
令\(\frac{dQ_C}{dI}=0\),得\(I = \frac{(\alpha_P - \alpha_N) T_C}{R}\),带入式(14)中得\(Q_{Cmax}\)
1.2.3 最大制冷系数
通过式(16)发现,制冷片两侧的温差越小,傅立叶效应对制冷量的影响越小,制冷系数就越高。通入的电流过小或者过大制冷片都将无法制冷,该式中,制冷系数是电流的函数,且制冷系数还和温差有关。式(16)关于\(I\)的求导,得到制冷系数的极值,获得最大制冷系数
其中,\(T_m\)为平均温度;\(Z\)为优值系数,\(Z\)的值由材料的物料特性决定,令\(M = \sqrt{1+ZT_m}\),代入到式(20)中的\(I_{opt}\)
此时的工作电压为\(U_{opt}\)
此时TEC的输入功率\(P_{opt}\)
将\(I_{opt}\)代入效率公式中
可知,工作温度一定的情况下,Z值越高制冷性能越好,制冷效率越高,此时最大制冷量\(Q_{opt}\)
不同的温差对应不同的最佳制冷效率,与最大制冷量的电流相比,最优电流值要小于最大制冷量时的电流值。
1.2.4 最大温差
根据式(14)可知温差\(\Delta T\)
同样可知\(\Delta T\)是电流的函数,关于\(I\)求导可得
上式可得:\(I = \frac{(\alpha_P - \alpha_N) T_C}{R}\),得到最大温差\(\Delta T_{max}\)
Note:在对使用严格、对温度反应敏感的电子元器件、对精密的恒温器以及其他精密的测量仪器应用领域,为维持低温或者某一恒温而又间歇式工作的情况,通常采用最大制冷量设计,该方案所用电子元件较少、体积较小、制造成本较低,但是制冷效率低、耗电较多、热端散热量较大;对于便携式野外冷热箱等连续性工作的制冷器,通常采用最大制冷系数要求设计,该方案制冷效率高、运行经济型较好、耗电以及热端散热量较少,但所需电子元件多、体积较大、制造成本高。
2. 热电冷却器选型
2.1 热电冷却器参数
| 参数 | 说明 |
|---|---|
| \(Q_{cmax}\) | 冷热面温差为0\(℃\)时,热电冷却器能够转移的热量 |
| \(I_{max}\) | 热电冷却器通过的最大电流,工作电流建议不超过\(70\% \;I_{max}\) |
| \(V_{max}\) | 热电冷却器通过最大电流时,两端的电压,工作电压建议也不超过\(70\% \;V_{max}\) |
| \(DT_{max}\) | 热电冷却器通过最大电流时,并且无任何热量输入时,冷热面的最大温差 |
| \(COP\) | 综合性能指数,冷却热量值与输入能量之间的比值(\(Q_c / U \cdot I\)) |
| \(T_h\) | 热电冷却器热端温度 |
| \(R_{AC}\) | 热电冷却器电阻 |
其中 \(Q_{cmax}\) 的测试条件是:测试时,TEC的热端连接的散热器可将热端温度降至与冷端始终相同,确保产生的热量被瞬间移走,即测试时 \(\Delta T = 0\) ,不会对TEC产生额外的热负荷。这是因为热量总是从高温传向低温,TEC工作时就是将冷端的热量按照逆温度梯度的方向传递到热端。
Note:热电冷却器的电气参数随环境温度变化而异。
2.2 选型案例
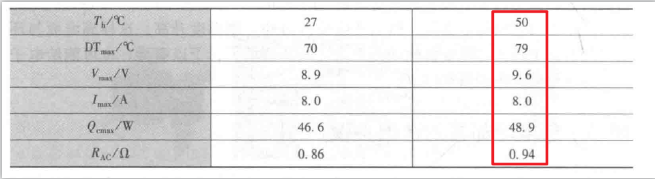
问题:如表为某TEC电气参数表(TEC规格书中也会给出电压、电流和温差线图),现取热端温度(连接散热器底端所能维持的温度)为50℃时的性能参数;应用场景为发热芯片20W,要求芯片温度控制在26℃,计算TEC的工作点(工作电压和工作电流)
(1)确定工作电流
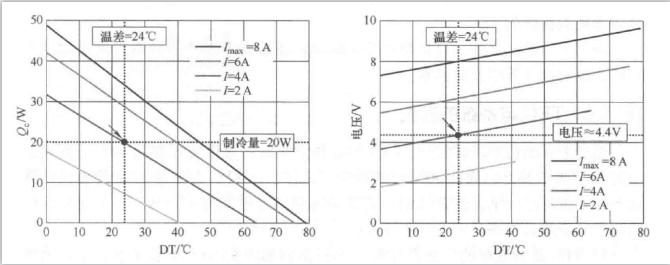
案例中,温差\(\Delta T=50-26=24 ℃\),查询制冷功率、电流、温差曲线图得,此时的工作电流为4A,在计算温差时忽略了两个因素:
- 忽略了TEC和芯片之间的接触热阻,因此在实际的设计中,冷端温度要保证低于芯片目标温度;
- 忽略了散热路径,散热路径非一维,这里假设所有的热量通过TEC吸收,这样制冷功率>发热量,保证满足实际使用要求。
(2)确定工作电压
(1)中确定了工作电流,根据温差、电压、电流曲线查的4A电流下、温差24℃时的电压为4.4V,因此工作电压为4.4V。那么可以计算\(COP\)综合效率系数的值:\(COP = \frac{Q_c}{UI} = \frac{20}{4 \times 4.4}=1.14\).
(3)确定COP值和选择高效TEC的迭代方式
COP值的确定也可以通过COP、电压、温差线图中查到,对于单层的TEC,COP通常介于0.4~0.7之间。对于TEC的迭代方案,要看其综合效率系数位于峰值点的哪一侧,根据这一点来优化选型方案:
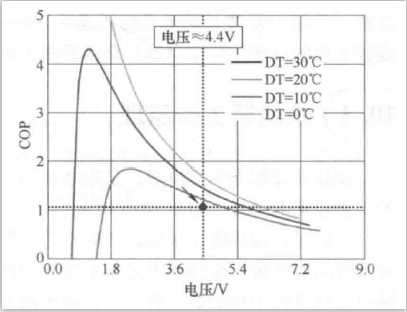
- 如果实际计算的COP点位于峰值左侧,那么说明输入功率过剩,即制冷能力过剩,可选用制冷能力稍弱的TEC;
- 如果实际计算的COP点位于峰值右侧,那么说明TEC制冷能力欠缺,需要选用制冷能力更强的TEC。
Note:COP值可以理解成单位功率下TEC所能“转移”的热量,当COP值较小时,系统能耗增加,同时还会增加散热器热负荷,加重系统的热量转移负担。
本文来自博客园,作者:code_wss,转载请注明原文链接:https://www.cnblogs.com/jxsme/p/18668061


 浙公网安备 33010602011771号
浙公网安备 33010602011771号