BUAA-OO-2021 第一单元作业
BUAA OO 第一单元总结
第一次作业
设计思路
总体思路
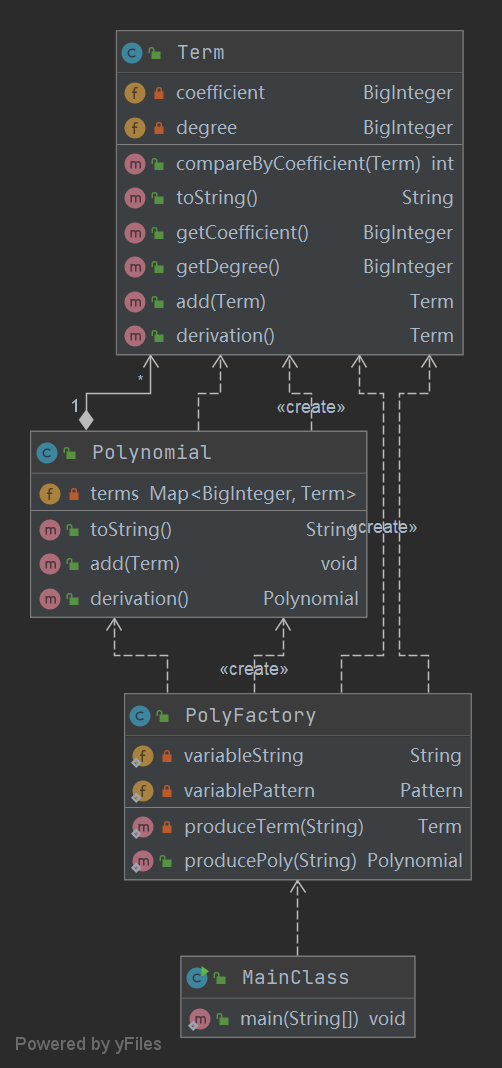
第一次作业还比较面向过程,本人采用PolyFactory 类用来处理输入同时生成Polynomial类和Term类。
Polynomial 类用来维护整个表达式,Term 类用了维护每个项的系数和幂次。
输入处理
PolyFactory 类中采用不断replace和split的方式分割了每个项,再对项分割因子。
求导思路
新建一个空的新Polynomial,对旧Polynomial的每个Term求导,再依次加入新Polynomial。
化简思路
- 合并同类项,这个用hashmap维护即可。
- 优先输出系数为正的项,这样可以省一个负号,toString的时候排个序就行了。
- \(x**1\to x\),toString的时候特判即可。
- \(1*x**k\to x**k,-1*x**k\to -x**k\),toString的时候特判即可。
- \(x**2\to x*x\),toString的时候特判即可。
类关系图
复杂度分析
方法复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| MainClass.main(String[]) | 0 | 1 | 1 | 1 |
| PolyFactory.producePoly(String) | 3 | 1 | 3 | 4 |
| PolyFactory.produceTerm(String) | 14 | 1 | 6 | 6 |
| Polynomial.Polynomial() | 0 | 1 | 1 | 1 |
| Polynomial.add(Term) | 4 | 1 | 3 | 3 |
| Polynomial.derivation() | 1 | 1 | 2 | 2 |
| Polynomial.toString() | 2 | 2 | 2 | 3 |
| Term.Term(BigInteger,BigInteger) | 0 | 1 | 1 | 1 |
| Term.add(Term) | 0 | 1 | 1 | 1 |
| Term.compareByCoefficient(Term) | 0 | 1 | 1 | 1 |
| Term.derivation() | 0 | 1 | 1 | 1 |
| Term.getCoefficient() | 0 | 1 | 1 | 1 |
| Term.getDegree() | 0 | 1 | 1 | 1 |
| Term.toString() | 9 | 2 | 5 | 6 |
类复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| MainClass | 1 | 1 | 1 |
| PolyFactory | 4.5 | 6 | 9 |
| Polynomial | 2.25 | 3 | 9 |
| Term | 1.71 | 6 | 12 |
代码行数

复杂度评价
整体来说这次作业难度较低,因此代码也比较简单,基本符合高内聚低耦合的设计准则。
其中PolyFactory的OCavg偏高,原因是PolyFactory的produceTerm函数写的比较复杂,用了很多特判,比较面向过程。
测试相关
本人强测与互测均未被发现BUG,并成功hack别人两次,hack时没有看别人代码而是进行黑盒测试。
hack数据为手动构造,主要利用爆栈hack了用了正则的代码。
自己写了自动测评机来找自己的BUG和hack别人的代码,但测评机没有成功hack到别人的代码。
第二次作业
设计思路
总体思路
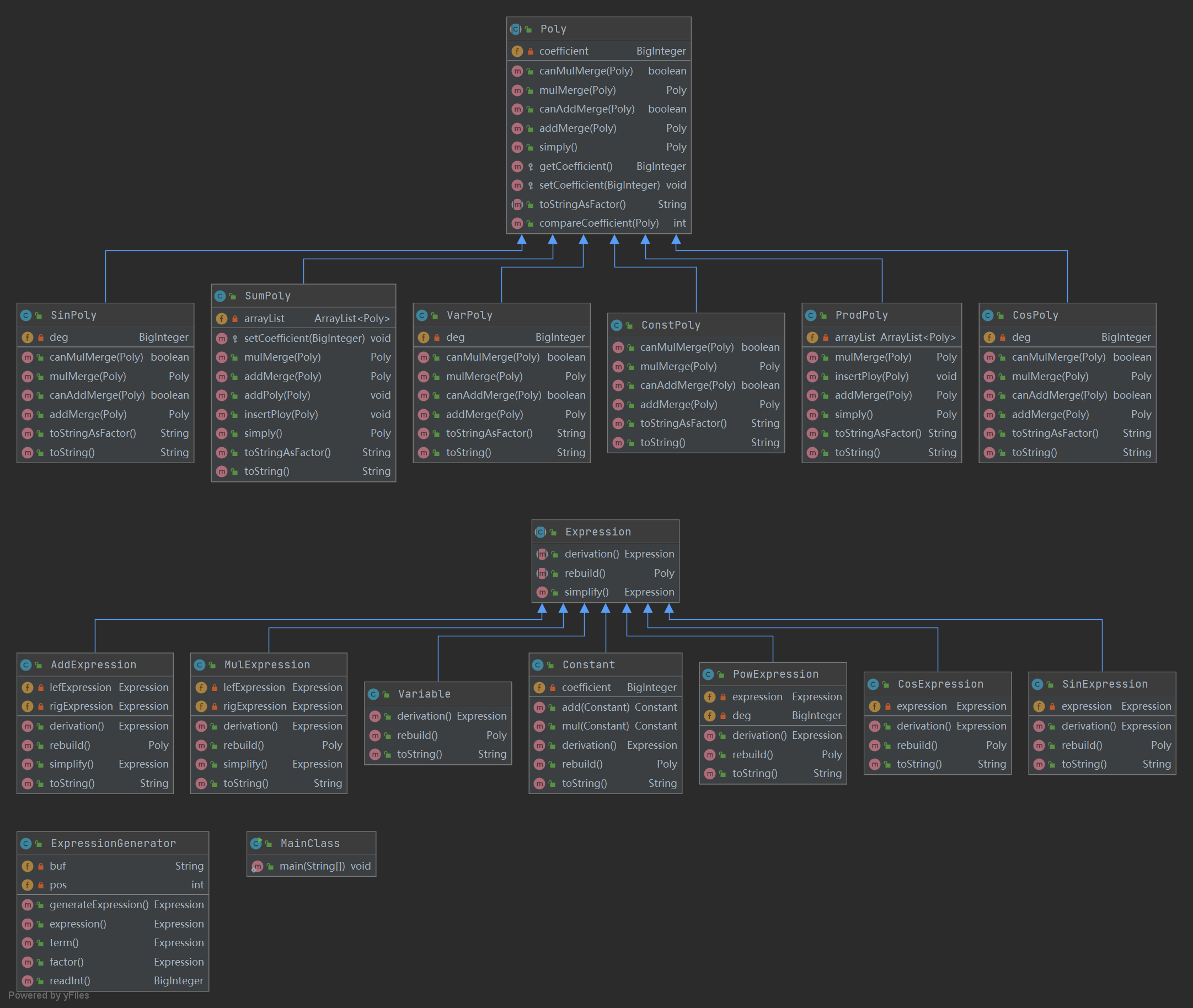
第二次作业开始面向对象了,其中ExpressionGenerator用于处理输入同时生成Expression类。
Expression类用于求导,Poly类用于化简。
输入处理
自学并实现了递归下降,处理式子前直接replace了空白字符和多重正负号,因此实现过程中暂时没有实现 Wrong Format的判定和处理。
求导思路
首先分析式子,发现式子仅包含常数,变量,\(\sin\) 函数,cos函数,幂函数,加法,减法,乘法。
归根到底,常量、变量、单/二元操作符。
而对于求导,不难发现,求导最底层一定是 \(常数'=0,x'=1\),然后通过各种单/二元操作符连接结果。
通过上述分析,很自然得到了对象的设计思路,对象即 \(x\) 和常数和所有单/二元操作符。
写一个抽象类 Expression,然后只需要 Expression 的所有子类支持求导即可,求导即按上述求导方法递归求解。
化简思路
- \(1*f(x)=f(x)\)
- \(0*f(x)=0\)
- \(f(x)^0=1\)
- \(f(x)^1=f(x)\)
- \(f(x)^a*f(x)^b=f(x)^{a+b}\)
- \(af(x)+bf(x)=(a+b)f(x)\)
- \((f(x))=f(x)\)
- \(x**2=x*x\)
- 正系数前移,例如 \(-x+x^2=x^2-x\)
专门为化简写了一个Poly类,Poly的每个子类支持化简simply,然后为每个类写一个加法合并函数addMerge和乘法合并函数mulMerge用于合并同类项。
类关系图
复杂度分析
方法复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| AddExpression.AddExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| AddExpression.derivation() | 0 | 1 | 1 | 1 |
| AddExpression.rebuild() | 0 | 1 | 1 | 1 |
| AddExpression.simplify() | 5 | 4 | 4 | 5 |
| AddExpression.toString() | 0 | 1 | 1 | 1 |
| ConstPoly.ConstPoly(BigInteger) | 0 | 1 | 1 | 1 |
| ConstPoly.addMerge(Poly) | 2 | 2 | 2 | 2 |
| ConstPoly.canAddMerge(Poly) | 0 | 1 | 1 | 1 |
| ConstPoly.canMulMerge(Poly) | 0 | 1 | 1 | 1 |
| ConstPoly.mulMerge(Poly) | 2 | 2 | 2 | 2 |
| ConstPoly.toString() | 0 | 1 | 1 | 1 |
| ConstPoly.toStringAsFactor() | 0 | 1 | 1 | 1 |
| Constant.Constant(BigInteger) | 0 | 1 | 1 | 1 |
| Constant.add(Constant) | 0 | 1 | 1 | 1 |
| Constant.derivation() | 0 | 1 | 1 | 1 |
| Constant.mul(Constant) | 0 | 1 | 1 | 1 |
| Constant.rebuild() | 0 | 1 | 1 | 1 |
| Constant.toString() | 0 | 1 | 1 | 1 |
| CosExpression.CosExpression(Expression) | 0 | 1 | 1 | 1 |
| CosExpression.derivation() | 0 | 1 | 1 | 1 |
| CosExpression.rebuild() | 0 | 1 | 1 | 1 |
| CosExpression.toString() | 0 | 1 | 1 | 1 |
| CosPoly.CosPoly(BigInteger) | 0 | 1 | 1 | 1 |
| CosPoly.CosPoly(BigInteger,BigInteger) | 0 | 1 | 1 | 1 |
| CosPoly.addMerge(Poly) | 6 | 4 | 4 | 4 |
| CosPoly.canAddMerge(Poly) | 2 | 2 | 2 | 2 |
| CosPoly.canMulMerge(Poly) | 0 | 1 | 1 | 1 |
| CosPoly.mulMerge(Poly) | 8 | 6 | 6 | 6 |
| CosPoly.toString() | 2 | 1 | 3 | 3 |
| CosPoly.toStringAsFactor() | 1 | 1 | 2 | 2 |
| Expression.Expression() | 0 | 1 | 1 | 1 |
| Expression.simplify() | 0 | 1 | 1 | 1 |
| ExpressionGenerator.ExpressionGenerator(String) | 0 | 1 | 1 | 1 |
| ExpressionGenerator.expression() | 3 | 1 | 3 | 3 |
| ExpressionGenerator.factor() | 19 | 6 | 11 | 13 |
| ExpressionGenerator.generateExpression() | 0 | 1 | 1 | 1 |
| ExpressionGenerator.readInt() | 1 | 1 | 2 | 2 |
| ExpressionGenerator.term() | 2 | 1 | 2 | 2 |
| MainClass.main(String[]) | 3 | 3 | 2 | 3 |
| MulExpression.MulExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| MulExpression.derivation() | 0 | 1 | 1 | 1 |
| MulExpression.rebuild() | 0 | 1 | 1 | 1 |
| MulExpression.simplify() | 7 | 5 | 6 | 7 |
| MulExpression.toString() | 2 | 1 | 1 | 3 |
| Poly.Poly(BigInteger) | 0 | 1 | 1 | 1 |
| Poly.addMerge(Poly) | 0 | 1 | 1 | 1 |
| Poly.canAddMerge(Poly) | 0 | 1 | 1 | 1 |
| Poly.canMulMerge(Poly) | 0 | 1 | 1 | 1 |
| Poly.compareCoefficient(Poly) | 0 | 1 | 1 | 1 |
| Poly.getCoefficient() | 0 | 1 | 1 | 1 |
| Poly.mulMerge(Poly) | 0 | 1 | 1 | 1 |
| Poly.setCoefficient(BigInteger) | 0 | 1 | 1 | 1 |
| Poly.simply() | 0 | 1 | 1 | 1 |
| PowExpression.PowExpression(Expression,BigInteger) | 0 | 1 | 1 | 1 |
| PowExpression.derivation() | 3 | 3 | 3 | 3 |
| PowExpression.rebuild() | 4 | 4 | 1 | 4 |
| PowExpression.toString() | 3 | 3 | 3 | 3 |
| ProdPoly.ProdPoly() | 0 | 1 | 1 | 1 |
| ProdPoly.addMerge(Poly) | 2 | 2 | 2 | 2 |
| ProdPoly.insertPloy(Poly) | 7 | 4 | 4 | 4 |
| ProdPoly.mulMerge(Poly) | 4 | 1 | 3 | 3 |
| ProdPoly.simply() | 6 | 3 | 5 | 5 |
| ProdPoly.toString() | 4 | 2 | 5 | 5 |
| ProdPoly.toStringAsFactor() | 0 | 1 | 1 | 1 |
| SinExpression.SinExpression(Expression) | 0 | 1 | 1 | 1 |
| SinExpression.derivation() | 0 | 1 | 1 | 1 |
| SinExpression.rebuild() | 0 | 1 | 1 | 1 |
| SinExpression.toString() | 0 | 1 | 1 | 1 |
| SinPoly.SinPoly(BigInteger) | 0 | 1 | 1 | 1 |
| SinPoly.SinPoly(BigInteger,BigInteger) | 0 | 1 | 1 | 1 |
| SinPoly.addMerge(Poly) | 6 | 4 | 4 | 4 |
| SinPoly.canAddMerge(Poly) | 2 | 2 | 2 | 2 |
| SinPoly.canMulMerge(Poly) | 0 | 1 | 1 | 1 |
| SinPoly.mulMerge(Poly) | 8 | 6 | 6 | 6 |
| SinPoly.toString() | 2 | 1 | 3 | 3 |
| SinPoly.toStringAsFactor() | 1 | 1 | 2 | 2 |
| SumPoly.SumPoly() | 0 | 1 | 1 | 1 |
| SumPoly.SumPoly(BigInteger,ArrayList |
0 | 1 | 1 | 1 |
| SumPoly.addMerge(Poly) | 0 | 1 | 1 | 1 |
| SumPoly.addPoly(Poly) | 4 | 1 | 3 | 3 |
| SumPoly.insertPloy(Poly) | 6 | 4 | 4 | 4 |
| SumPoly.mulMerge(Poly) | 4 | 4 | 4 | 4 |
| SumPoly.setCoefficient(BigInteger) | 1 | 1 | 2 | 2 |
| SumPoly.simply() | 5 | 3 | 4 | 4 |
| SumPoly.toString() | 2 | 2 | 2 | 3 |
| SumPoly.toStringAsFactor() | 2 | 2 | 2 | 3 |
| VarPoly.VarPoly(BigInteger) | 0 | 1 | 1 | 1 |
| VarPoly.VarPoly(BigInteger,BigInteger) | 0 | 1 | 1 | 1 |
| VarPoly.addMerge(Poly) | 6 | 4 | 4 | 4 |
| VarPoly.canAddMerge(Poly) | 2 | 2 | 2 | 2 |
| VarPoly.canMulMerge(Poly) | 0 | 1 | 1 | 1 |
| VarPoly.mulMerge(Poly) | 8 | 6 | 6 | 6 |
| VarPoly.toString() | 2 | 1 | 3 | 3 |
| VarPoly.toStringAsFactor() | 4 | 1 | 3 | 3 |
| Variable.Variable() | 0 | 1 | 1 | 1 |
| Variable.derivation() | 0 | 1 | 1 | 1 |
| Variable.rebuild() | 0 | 1 | 1 | 1 |
| Variable.toString() | 0 | 1 | 1 | 1 |
类复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| AddExpression | 1.6 | 4 | 8 |
| ConstPoly | 1.29 | 2 | 9 |
| Constant | 1 | 1 | 6 |
| CosExpression | 1 | 1 | 4 |
| CosPoly | 2.5 | 6 | 20 |
| Expression | 1 | 1 | 2 |
| ExpressionGenerator | 3.33 | 12 | 20 |
| MainClass | 3 | 3 | 3 |
| MulExpression | 2.2 | 5 | 11 |
| Poly | 1 | 1 | 9 |
| PowExpression | 2.75 | 4 | 11 |
| ProdPoly | 2.86 | 5 | 20 |
| SinExpression | 1 | 1 | 4 |
| SinPoly | 2.5 | 6 | 20 |
| SumPoly | 2.6 | 4 | 26 |
| VarPoly | 2.62 | 6 | 21 |
| Variable | 1 | 1 | 4 |
代码行数
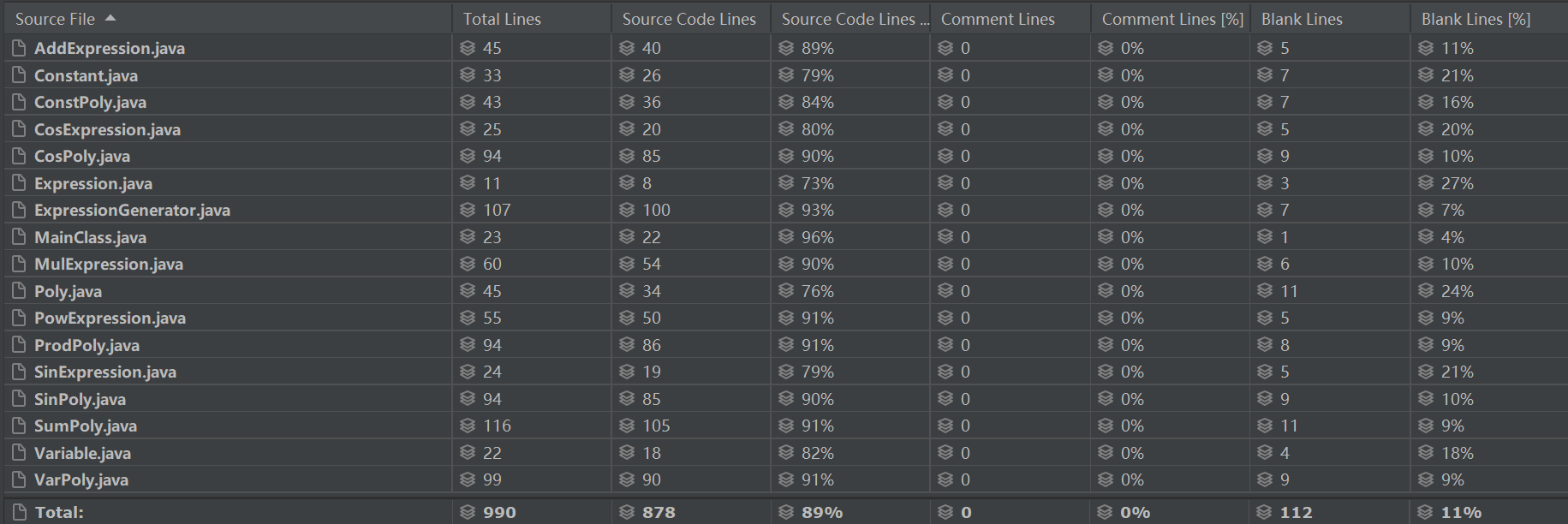
复杂度评价
用于Poly类的设计不佳,导致合并同类项的过程异常繁琐,需要各种判定,导致Poly类中各个子类的addMerge和mulMerge函数的圈复杂度普遍偏高,同时代码量也直线上升。
同时本次作业采用二叉树求导和多叉树化简,同时需要实现二者之间的相互转换,这也导致了代码量的上升。
另外ExpressionGenerator类的复杂度也较大,主要原因是在递归下降中用了过多的条件判断语句。
测试相关
本人强测与互测均未被发现BUG,并成功hack别人三次,hack时没有看别人代码而是进行黑盒测试。
hack数据为手动构造,主要利用表达式套娃hack成功两次,另外通过 \(\sin^2(x)+\cos^2(x)\) hack到别人一次,估计是别人忘了判定表达式求导并化简后为空的情况。
自己写了自动测评机来找自己的BUG和hack别人的代码,但测评机没有成功hack到别人的代码。
第三次作业
设计思路
总体思路
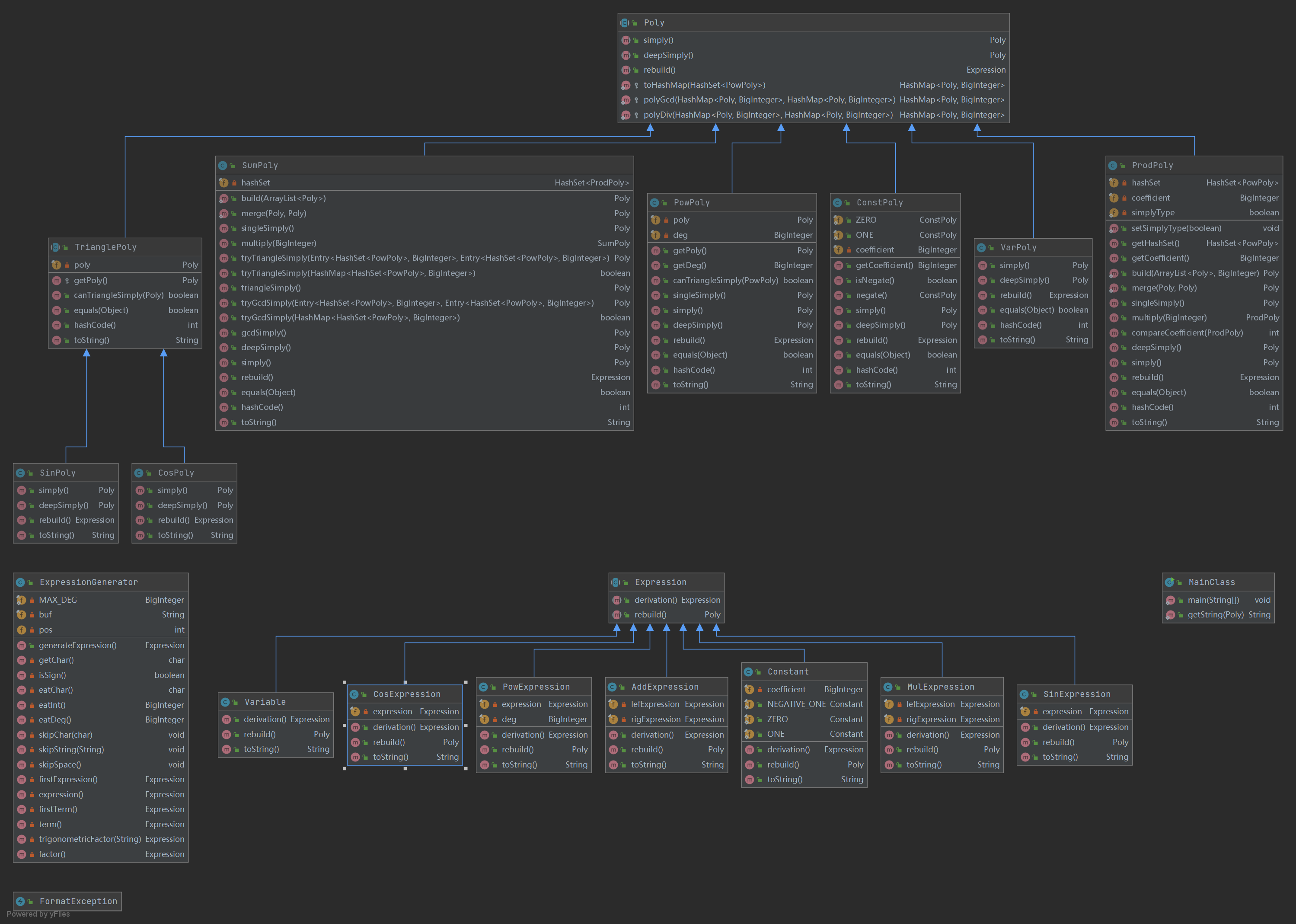
第三次作业主要在第二次作业上重构了化简类,第二次作业的求导类已经满足第三次作业的需求了。
输入处理
对递归下降进行了调整,感觉算法更接近自动机了,完全依照指导书的形式化表达来构建代码,实现了 Wrong Format的判定和处理,自动机流程如下图。
求导思路
由于第二次作业已经满足第三次作业的求导需求,因此没有修改。
化简思路
-
\(1*f(x)=f(x)\)
-
\(0*f(x)=0\)
-
\(f(x)^0=1\)
-
\(f(x)^1=f(x)\)
-
\(f(x)^a*f(x)^b=f(x)^{a+b}\)
-
\(af(x)+bf(x)=(a+b)f(x)\)
-
\((f(x))=f(x)\)
-
\(\sin(0)=0\)
-
\(\cos(0)=1\)
-
\(\cos(-a)=\cos(a)(a\gt 0)\)
-
\(x**2=x*x\)
-
正系数前移,例如 \(-x+x^2=x^2-x\)
-
\(a\sin^2(f(x))g(x)+b\cos^2(f(x))g(x)=ag(x)+(b-a)\cos^2(f(x))g(x)(a\le b)\)
-
\(f(x)h(x)+g(x)h(x)=(f(x)+g(x))h(x)\)
-
\(\cos((-1*\text{变量因子}^k))=\cos(\text{变量因子}^k)\)
-
乘法展开
同类项合并优化
利用多叉树和hashMap实现项的合并,于是首先需要实现同类项判定。
完全正确的同类项判定是非常困难的,这里只考虑同类项判定的充分不必要条件。
对于三角函数直接判定三角函数类型以及内部是否相同即可,对幂函数判定幂函数底数和指数即可。
对连加类和连乘类用hashset 维护内容,然后直接调用 hashset 的 equal 即可。
显然这样并不会将 \(\cos(2x)\) 和 \(\cos^2(x)-\sin^2(x)\) 判定相等,但大部分相等的式子还是可以正确判定的。
而且误将相等的式子判定为不相等并不会影响程序正确性,最多影响一点性能。
另外根据第二次作业失败经验,本次连乘类和连加类对子项类型进行了统一化处理,这样可以避免大量分类讨论。
连乘类的每个项必须是幂函数形式,同时维护一个系数。对于连加类,强制每个项必须是连乘项。
对于连乘项,合并同类项时开一个hashmap 记录每个因子的幂次,最后删除幂次为0的因子再重新生成 hashset
对于连加项,合并同类项时开一个hashmap记录每个项的系数,最后删除系数为0的因子再重新生成 hashset 。
括号嵌套的优化
递归调用子项的化简函数,然后对与连加和连乘项,特判子项个数为 \(1\) 的情况然后把子项提出来。
cos偶函数优化
化简时特判即可。
x*x优化
toString时特判即可,注意 \(\sin(x*x)\) 和 \(\cos(x*x)\) 非法。
正系数前移优化
toString时对连加项中的连乘项根据系数进行排序。
三角优化
简单来说,对连加式,暴力二重遍历它的连乘项,对两个连乘项,考虑用两个 hashmap 维护两个连乘项因子的幂次,然后再求 \(min\),最后如果两个 hashmap 除以公因项后的内容正好是 \(a\sin^2(f(x))+b\cos^2(f(x))\) 的形式,直接合并即可,一直操作直到不存在可以合并的项位置。
因式分解优化
类似三角优化,合并条件改为公因子非空时进行合并。
乘法展开优化
本人只处理了常数乘以连加式的展开,仅需要更新连乘类的系数即可。
不稳定优化处理方案
对因式分解优化和乘法展开优化,最后结果有可能边长也有可能变短,于是本人考虑都试一遍然后取最短结果。
类关系图
复杂度分析
方法复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| ExpressionGenerator.ExpressionGenerator(String) | 2 | 2 | 2 | 3 |
| ExpressionGenerator.eatChar() | 0 | 1 | 1 | 1 |
| ExpressionGenerator.eatDeg() | 2 | 2 | 2 | 3 |
| ExpressionGenerator.eatInt() | 5 | 3 | 5 | 7 |
| ExpressionGenerator.expression() | 7 | 4 | 4 | 5 |
| ExpressionGenerator.factor() | 7 | 6 | 8 | 8 |
| ExpressionGenerator.firstExpression() | 6 | 2 | 4 | 5 |
| ExpressionGenerator.firstTerm() | 6 | 2 | 5 | 6 |
| ExpressionGenerator.generateExpression() | 1 | 2 | 1 | 2 |
| ExpressionGenerator.getChar() | 0 | 1 | 1 | 1 |
| ExpressionGenerator.isSign() | 1 | 1 | 2 | 2 |
| ExpressionGenerator.skipChar(char) | 1 | 2 | 1 | 2 |
| ExpressionGenerator.skipSpace() | 2 | 1 | 2 | 3 |
| ExpressionGenerator.skipString(String) | 1 | 1 | 2 | 2 |
| ExpressionGenerator.term() | 4 | 2 | 4 | 4 |
| ExpressionGenerator.trigonometricFactor(String) | 2 | 2 | 2 | 2 |
| FormatException.FormatException() | 0 | 1 | 1 | 1 |
| MainClass.getString(Poly) | 1 | 1 | 2 | 2 |
| MainClass.main(String[]) | 4 | 1 | 2 | 5 |
| expression.AddExpression.AddExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| expression.AddExpression.derivation() | 0 | 1 | 1 | 1 |
| expression.AddExpression.rebuild() | 0 | 1 | 1 | 1 |
| expression.AddExpression.toString() | 0 | 1 | 1 | 1 |
| expression.Constant.Constant(BigInteger) | 0 | 1 | 1 | 1 |
| expression.Constant.derivation() | 0 | 1 | 1 | 1 |
| expression.Constant.rebuild() | 0 | 1 | 1 | 1 |
| expression.Constant.toString() | 0 | 1 | 1 | 1 |
| expression.CosExpression.CosExpression(Expression) | 0 | 1 | 1 | 1 |
| expression.CosExpression.derivation() | 0 | 1 | 1 | 1 |
| expression.CosExpression.rebuild() | 0 | 1 | 1 | 1 |
| expression.CosExpression.toString() | 0 | 1 | 1 | 1 |
| expression.MulExpression.MulExpression(Expression,Expression) | 0 | 1 | 1 | 1 |
| expression.MulExpression.derivation() | 0 | 1 | 1 | 1 |
| expression.MulExpression.rebuild() | 0 | 1 | 1 | 1 |
| expression.MulExpression.toString() | 2 | 1 | 1 | 3 |
| expression.PowExpression.PowExpression(Expression,BigInteger) | 0 | 1 | 1 | 1 |
| expression.PowExpression.derivation() | 3 | 3 | 3 | 3 |
| expression.PowExpression.rebuild() | 0 | 1 | 1 | 1 |
| expression.PowExpression.toString() | 3 | 3 | 3 | 3 |
| expression.SinExpression.SinExpression(Expression) | 0 | 1 | 1 | 1 |
| expression.SinExpression.derivation() | 0 | 1 | 1 | 1 |
| expression.SinExpression.rebuild() | 0 | 1 | 1 | 1 |
| expression.SinExpression.toString() | 0 | 1 | 1 | 1 |
| expression.Variable.Variable() | 0 | 1 | 1 | 1 |
| expression.Variable.derivation() | 0 | 1 | 1 | 1 |
| expression.Variable.rebuild() | 0 | 1 | 1 | 1 |
| expression.Variable.toString() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.ConstPoly(BigInteger) | 0 | 1 | 1 | 1 |
| poly.ConstPoly.deepSimply() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.equals(Object) | 3 | 3 | 2 | 4 |
| poly.ConstPoly.getCoefficient() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.hashCode() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.isNegate() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.negate() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.rebuild() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.simply() | 0 | 1 | 1 | 1 |
| poly.ConstPoly.toString() | 0 | 1 | 1 | 1 |
| poly.CosPoly.CosPoly(Poly) | 0 | 1 | 1 | 1 |
| poly.CosPoly.deepSimply() | 4 | 4 | 4 | 4 |
| poly.CosPoly.rebuild() | 0 | 1 | 1 | 1 |
| poly.CosPoly.simply() | 4 | 4 | 4 | 4 |
| poly.CosPoly.toString() | 0 | 1 | 1 | 1 |
| poly.Poly.polyDiv(HashMap<Poly, BigInteger>,HashMap<Poly, BigInteger>) | 1 | 1 | 2 | 2 |
| poly.Poly.polyGcd(HashMap<Poly, BigInteger>,HashMap<Poly, BigInteger>) | 3 | 1 | 3 | 3 |
| poly.Poly.toHashMap(HashSet |
1 | 1 | 2 | 2 |
| poly.PowPoly.PowPoly(Poly) | 2 | 1 | 2 | 2 |
| poly.PowPoly.PowPoly(Poly,BigInteger) | 0 | 1 | 1 | 1 |
| poly.PowPoly.canTriangleSimply(PowPoly) | 2 | 2 | 4 | 4 |
| poly.PowPoly.deepSimply() | 0 | 1 | 1 | 1 |
| poly.PowPoly.equals(Object) | 4 | 3 | 3 | 5 |
| poly.PowPoly.getDeg() | 0 | 1 | 1 | 1 |
| poly.PowPoly.getPoly() | 0 | 1 | 1 | 1 |
| poly.PowPoly.hashCode() | 0 | 1 | 1 | 1 |
| poly.PowPoly.rebuild() | 0 | 1 | 1 | 1 |
| poly.PowPoly.simply() | 0 | 1 | 1 | 1 |
| poly.PowPoly.singleSimply() | 5 | 4 | 4 | 5 |
| poly.PowPoly.toString() | 9 | 1 | 7 | 7 |
| poly.ProdPoly.ProdPoly(HashMap<Poly, BigInteger>,BigInteger) | 1 | 1 | 2 | 2 |
| poly.ProdPoly.ProdPoly(HashSet |
0 | 1 | 1 | 1 |
| poly.ProdPoly.ProdPoly(Poly) | 3 | 1 | 3 | 3 |
| poly.ProdPoly.build(ArrayList |
2 | 1 | 3 | 3 |
| poly.ProdPoly.compareCoefficient(ProdPoly) | 0 | 1 | 1 | 1 |
| poly.ProdPoly.deepSimply() | 5 | 1 | 4 | 4 |
| poly.ProdPoly.equals(Object) | 4 | 3 | 3 | 5 |
| poly.ProdPoly.getCoefficient() | 0 | 1 | 1 | 1 |
| poly.ProdPoly.getHashSet() | 0 | 1 | 1 | 1 |
| poly.ProdPoly.hashCode() | 0 | 1 | 1 | 1 |
| poly.ProdPoly.merge(Poly,Poly) | 0 | 1 | 1 | 1 |
| poly.ProdPoly.multiply(BigInteger) | 0 | 1 | 1 | 1 |
| poly.ProdPoly.rebuild() | 6 | 1 | 3 | 5 |
| poly.ProdPoly.setSimplyType(boolean) | 0 | 1 | 1 | 1 |
| poly.ProdPoly.simply() | 5 | 1 | 4 | 4 |
| poly.ProdPoly.singleSimply() | 21 | 9 | 11 | 12 |
| poly.ProdPoly.toString() | 10 | 2 | 5 | 5 |
| poly.SinPoly.SinPoly(Poly) | 0 | 1 | 1 | 1 |
| poly.SinPoly.deepSimply() | 1 | 2 | 1 | 2 |
| poly.SinPoly.rebuild() | 0 | 1 | 1 | 1 |
| poly.SinPoly.simply() | 1 | 2 | 1 | 2 |
| poly.SinPoly.toString() | 0 | 1 | 1 | 1 |
| poly.SumPoly.SumPoly(HashSet |
0 | 1 | 1 | 1 |
| poly.SumPoly.SumPoly(Poly) | 2 | 1 | 2 | 2 |
| poly.SumPoly.build(ArrayList |
2 | 1 | 3 | 3 |
| poly.SumPoly.deepSimply() | 6 | 1 | 5 | 5 |
| poly.SumPoly.equals(Object) | 3 | 3 | 2 | 4 |
| poly.SumPoly.gcdSimply() | 3 | 1 | 3 | 4 |
| poly.SumPoly.hashCode() | 0 | 1 | 1 | 1 |
| poly.SumPoly.merge(Poly,Poly) | 0 | 1 | 1 | 1 |
| poly.SumPoly.multiply(BigInteger) | 1 | 1 | 2 | 2 |
| poly.SumPoly.rebuild() | 5 | 1 | 3 | 4 |
| poly.SumPoly.simply() | 5 | 1 | 4 | 4 |
| poly.SumPoly.singleSimply() | 3 | 3 | 3 | 3 |
| poly.SumPoly.toString() | 1 | 1 | 2 | 2 |
| poly.SumPoly.triangleSimply() | 3 | 1 | 3 | 4 |
| poly.SumPoly.tryGcdSimply(Entry<HashSet |
4 | 3 | 3 | 4 |
| poly.SumPoly.tryGcdSimply(HashMap<HashSet |
12 | 6 | 5 | 7 |
| poly.SumPoly.tryTriangleSimply(Entry<HashSet |
7 | 3 | 5 | 5 |
| poly.SumPoly.tryTriangleSimply(HashMap<HashSet |
12 | 6 | 5 | 7 |
| poly.TrianglePoly.TrianglePoly(Poly) | 0 | 1 | 1 | 1 |
| poly.TrianglePoly.canTriangleSimply(Poly) | 3 | 3 | 3 | 3 |
| poly.TrianglePoly.equals(Object) | 3 | 3 | 2 | 4 |
| poly.TrianglePoly.getPoly() | 0 | 1 | 1 | 1 |
| poly.TrianglePoly.hashCode() | 0 | 1 | 1 | 1 |
| poly.TrianglePoly.toString() | 5 | 1 | 4 | 5 |
| poly.VarPoly.VarPoly() | 0 | 1 | 1 | 1 |
| poly.VarPoly.deepSimply() | 0 | 1 | 1 | 1 |
| poly.VarPoly.equals(Object) | 2 | 2 | 2 | 3 |
| poly.VarPoly.hashCode() | 0 | 1 | 1 | 1 |
| poly.VarPoly.rebuild() | 0 | 1 | 1 | 1 |
| poly.VarPoly.simply() | 0 | 1 | 1 | 1 |
| poly.VarPoly.toString() | 0 | 1 | 1 | 1 |
类复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| ExpressionGenerator | 2.62 | 6 | 42 |
| FormatException | 1 | 1 | 1 |
| MainClass | 3 | 4 | 6 |
| expression.AddExpression | 1 | 1 | 4 |
| expression.Constant | 1 | 1 | 4 |
| expression.CosExpression | 1 | 1 | 4 |
| expression.Expression | n/a | n/a | 0 |
| expression.MulExpression | 1.5 | 3 | 6 |
| expression.PowExpression | 2 | 3 | 8 |
| expression.SinExpression | 1 | 1 | 4 |
| expression.Variable | 1 | 1 | 4 |
| poly.ConstPoly | 1.2 | 3 | 12 |
| poly.CosPoly | 2.2 | 4 | 11 |
| poly.Poly | 2.33 | 3 | 7 |
| poly.PowPoly | 1.92 | 5 | 23 |
| poly.ProdPoly | 2.71 | 9 | 46 |
| poly.SinPoly | 1.4 | 2 | 7 |
| poly.SumPoly | 3.22 | 6 | 58 |
| poly.TrianglePoly | 2 | 3 | 12 |
| poly.VarPoly | 1.14 | 2 | 8 |
代码行数


复杂度评价
为了追求更好的性能,导致部分Poly的化简函数复杂度较高,特别是SumPoly的三角函数合并与因式分解合并显得异常复杂,代码行数也直线上升。
另外由于增加了Wrong Format的判定和处理,导致递归下降复杂度再次上升。
测试相关
本人强测未被发现BUG,互测被hack一次同时成功hack别人两次,hack时没有看别人代码而是进行黑盒测试。
hack数据为自动测评机构造,我本人也不清楚为什么别人会有这个BUG,只能说题目一旦复杂就什么BUG都有。
本人BUG为因式分解导致的BUG,触发原因为因式分解导致PowPoly的底数性质发生变化然而自己却忘记考虑了这种情况。
本质原因为为追求更好的性能导致代码过与复杂导致的BUG,这教会我以后要在性能分和正确性中做到更好的平衡。
重构经历总结
第一次作业的框架完全不能应用于第二次作业,于是第二次作业时对整个代码进行了重构。
第二次作业的求导框架已经提前考虑了第三次作业的要求,可拓展性较强,直接沿用到了第三次作业。
第三次作业重构了第二次作业的化简框架,类的复杂度上升的同时化简功能也强大了不少。
总的来说,本次作业重构了1.5次,还算可以接受。
心得体会
本次作业让我充分理解了面向对象的优势,实现了从面向过程编程到面向对象编程的转变。
同时为了处理输入我还学会了一部分编译原理,理解了正则表达式状态机的搭建、LL(1)文法和递归下降法。
另外我也明白了框架设计的重要性,如果一开始框架没设计好,通常来讲进行功能拓展时总会感到强大的阻力,同时需要通过各种判定语句来处理各种情况,最后必然导致重构。
最后,本次作业也锻炼了我利用python、c++构造自动测频机来找自己BUG和hack别人的能力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号