第七次作业:图的表示与遍历
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/qdu/DS2020 |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/qdu/DS2020/homework/11472 |
| 这个作业的目标 | 图的邻接矩阵和邻接表示、深度优先和广度优先搜索方法 |
| 学号 | 2018204261 |
一、实验目的
1、掌握图的邻接矩阵和邻接表表示
2、掌握图的深度优先和广度优先搜索方法
3、理解图的应用方法
二、实验预习
说明以下概念
1、深度优先搜索遍历:对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次.
2、广度优先搜索遍历:从某个顶点V出发,访问该顶点的所有邻接点V1,V2..VN;从邻接点V1,V2...VN出发,再访问他们各自的所有邻接点;重复上述步骤,直到所有的顶点都被访问过。
3、拓扑排序:对一个有向无环图G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。
4、最小生成树:一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
5、最短路径:用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
三、实验内容和要求
1、阅读并运行下面程序,根据输入写出运行结果。
#include<stdio.h>
#define N 20
#define TRUE 1
#define FALSE 0
int visited[N];
typedef struct{ /*队列的定义*/
int data[N];
int front,rear;
}queue;
typedef struct{ /*图的邻接矩阵*/
int vexnum,arcnum;
char vexs[N];
int arcs[N][N];
}graph;
void createGraph(graph *g);/*建立一个无向图的邻接矩阵*/
void dfs(int i,graph *g);/*从第i歌顶点出发深度优先搜索*/
void tdfs(graph *g); /*深度优先搜索整个图*/
void bfs(int k,graph *g);/*从第k个顶点广度优先搜索整个图*/
void tbfs(graph *g); /*广度优先搜索整个图*/
void init_visit(); /*初始化访问标识数组*/
void createGraph(graph *g){ /*建立一个无向图的邻接矩阵*/
int i,j;
char v;
g->vexnum=0;
g->arcnum=0;
i=0;
printf("输出顶点序列(以#结束):\n");
while(v=getchar()!='#')
{
g->vexs[i]=v; /*读入顶点信息*/
i++;
}
g->vexnum=i; /*顶点数目*/
for(i=0;i<g->vexnum;i++) /*邻接矩阵初始化*/
for(j=0;j<g->vexnum;j++)
g->arcs[i][j]=0;
printf("输入的信息:\n");
scanf("%d,%d",&i,&j); /*读入边i,j*/
while(i!=j) /*读入i,j为-1时结束*/
{
g->arcs[i][j]=1;
g->arcs[j][i]=1;
scanf("%d,%d",&i,&j);
}
}
void dfs(int i,graph *g){ /*从第i个顶点出发深度优先搜索*/
int j;
printf("%c",g->vexs[i]);
visited[i]=TRUE;
for(j=0;j<g->vexnum;j++)
if((g->arcs[i][j]==1)&&(!visited[j]))
dfs(j,g);
}
void tdfs(graph *g){ /*深度优先搜索整个图*/
int i;
printf("\n从顶点%c开始深度优先搜索序列:",g->vexs[0]);
for(i=0;i<g->vexnum;i++)
if(visited[i]!=TRUE)
dfs(i,g);
}
void bfs(int k,graph *g){ /*从第k个顶点出发广度优先搜索*/
int i,j;
queue qlist,*q;
q=&qlist;
q->rear=0;
q->front=0;
printf("%c",g->vexs[k]);
visited[k]=TRUE;
q->data[q->rear]=k;
q->rear=(q->rear+1)%N;
while(q->rear!=q->front)
{
i=q->data[q->front];
q->front=(q->front+1)%N;
for(j=0;j<g->vexnum;j++)
if((g->arcs[i][j]==1)&&(!visited[j]))
{
printf("%c",g->vexs[j]);
visited[j]=TRUE;
q->data[q->rear]=j;
q->rear=(q->rear+1)%N;
}
}
}
void tbfs(graph *g){ /*广度优先搜索整个图*/
int i;
printf("\n从顶点%c开始广度优先搜索序列:",g->vexs[0]);
for(i=0;i<g->vexnum;i++)
if(visited[i]!=TRUE)
bfs(i,g);
}
void init_visit(){ /*初始化访问标识数组*/
int i;
for(i=0;i<N;i++)
visited[i]=FALSE;
}
int main(){
graph ga;
int i,j;
createGraph(&ga);
printf("无向图的邻接矩阵:\n");
for(i=0;i<ga.vexnum;i++)
{
for(j=0;j<ga.vexnum;j++)
printf("%3d",ga.arcs[i][j]);
printf("\n");
}
init_visit();
tdfs(&ga);
init_visit();
tbfs(&ga);
return 0;
}
·根据右图的结构验证实验,
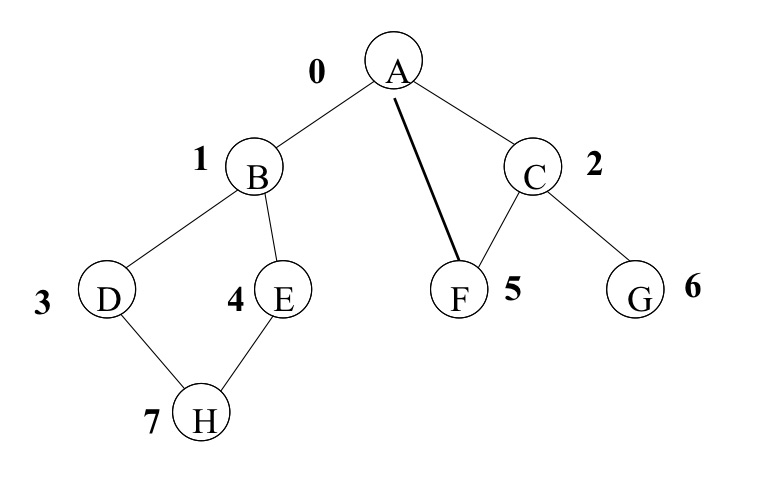
输入:
ABCDEFGH#
0,1
0,2
0,5
1,3
1,4
2,5
2,6
3,7
4,7
-1,-1
·运行结果:
2、阅读并运行下面程序,补充拓扑排序算法。
#include<stdio.h>
#include<malloc.h>
#define N 20
typedef struct edgenode{ /*图的邻接表:邻接链表结点*/
int adjvex; /*顶点序号*/
struct edgenode *next; /*下个结点的指针*/
}edgenode;
typedef struct vnode{ /*图的邻接表:邻接表*/
char data; /*顶点信息*/
int ind; /*顶点入度*/
struct edgenode *link; /*指向邻接链表指针*/
}vnode;
void createGraph_list(vnode adjlist[],int *p);/*建立有向图的邻接表*/
void topSort(vnode g[],int n);/*拓扑排序*/
void createGraph_list(vnode adjlist[],int *p){
int i,j,n,e;
char v;
edgenode *s;
i=0;n=0;e=0;
printf("输入顶点序列(以#结束):\n");
while((v=getchar())!='#')
{
adjlist[i].data=v; /*读入顶点信息*/
adjlist[i].link=NULL;
adjlist[i].ind=0;
i++;
}
n=i;
*p=n; /*建立邻接链表*/
printf("\n请输入弧的信息(i=-1结束):i,j:\n");
scanf("%d,%d",&i,&j);
while(i!=-1)
{
s=(struct edgenode*)malloc(sizeof(edgenode));
s->adjvex=j;
s->next=adjlist[i].link;
adjlist[i].link=s;
adjlist[j].ind++;/*顶点j的入度加1*/
e++;
scanf("%d,%d",&i,&j);
}
printf("邻接表:");
for(i=0;i<n;i++) /*输出邻接表*/
{
printf("\n%c,%d",adjlist[i].data,adjlist[i].ind);
s=adjlist[i].link;
while(s!=NULL)
{
printf("->%d",s->adjvex);
s=s->next;
}
}
}
void topSort(vnode g[],int n){
printf("输入拓扑排序顶点序列:\n");
int i,j,k,m=0,top=-1;
struct edgenode *p;
for (i=0; i<=n; i++) //将度为零的顶点入栈
if (g[i].ind==0)
{
g[i].ind=top;
top=i;
}
while (top!=-1) //栈不为空
{
j=top;
top=g[top].ind; //出栈
printf("%c",g[j].data);
m++;
p=g[j].link;
while (p) //删除该节点的所有边
{
k=p->adjvex;
g[k].ind--;
if (g[k].ind==0) //将入度为零的点入栈
{
g[k].ind=top;
top=k;
}
p=p->next;
}
}
if (m<n)
printf("该图存在环\n");
}
int main(){
vnode adjlist[N];
int n,*p;
p=&n;
createGraph_list(adjlist,p);
return 0;
}
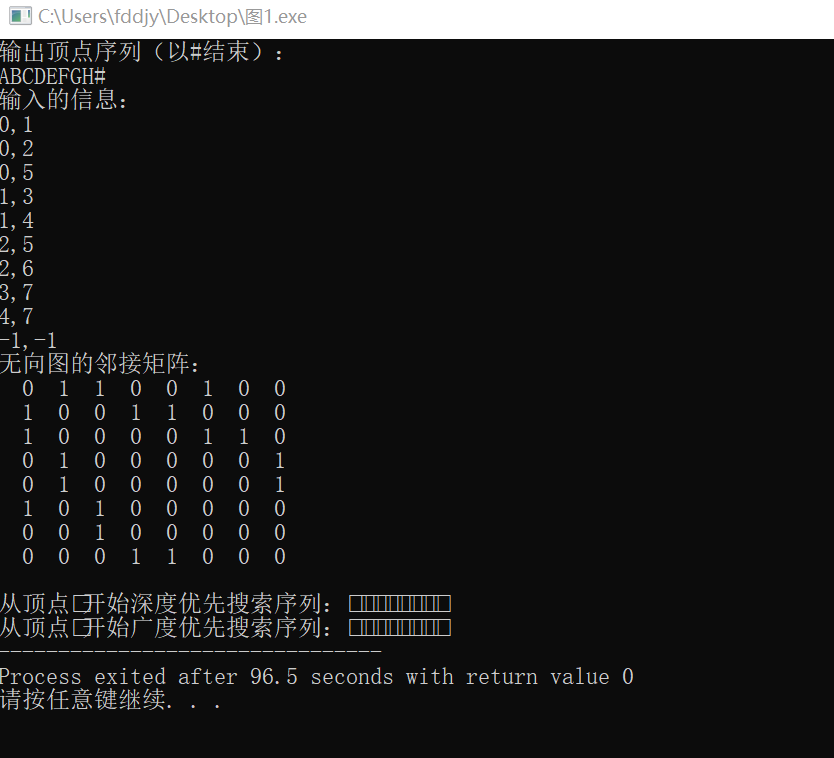
·根据输入,输出有向图的拓扑排序序列。并画出有向图。输入:
ABCDEF#
0,1
1,2
2,3
4,1
4,5
-1,-1
· 运行结果:
3、阅读并运行下面程序。
#include<stdio.h>
#define N 20
#define TRUE 1
#define INF 32766 /*邻接矩阵中的无穷大元素*/
#define INFIN 32767 /*比无穷大元素大的数*/
typedef struct{ /*图的邻接矩阵*/
int vexnum,arcnum;
char vexs[N];
int arcs[N][N];
}
graph;
void createGraph_w(graph *g,int flag);
void prim(graph *g,int u);
void dijkstra(graph g,int v);
void showprim();
void showdij();
/*建带权图的邻接矩阵,若flag为1则为无向图,flag为0为有向图*/
void createGraph_w(graph *g,int flag){
int i,j,w;
char v;
g->vexnum=0;
g->arcnum=0;
i=0;
printf("输入顶点序列(以#结束):\n");
while((v=getchar())!='#')
{
g->vexs[i]=v; /*读入顶点信息*/
i++;
}
g->vexnum=i;
for(i=0;i<6;i++) /*邻接矩阵初始化*/
for(j=0;j<6;j++)
g->arcs[i][j]=INF;
printf("输入边的信息:\n");
scanf("%d,%d,%d",&i,&j,&w); /*读入边(i,j,w)*/
while(i!=-1) /*读入i为-1时结束*/
{
g->arcs[i][j]=w;
if(flag==1)
g->arcs[j][i]=w;
scanf("%d,%d,%d",&i,&j,&w);
}
}
void prim(graph *g,int u)/*出发顶点u*/
{
int lowcost[N],closest[N],i,j,k,min;
for(i=0;i<g->vexnum;i++) /*求其他顶点到出发顶点u的权*/
{
lowcost[i]=g->arcs[u][i];
closest[i]=u;
}
lowcost[u]=0;
for(i=1;i<g->vexnum;i++) /*循环求最小生成树中的各条边*/
{ min=INFIN;
for(j=0;j<g->vexnum;j++) /*选择得到一条代价最小的边*/
if(lowcost[j]!=0&&lowcost[j]<min)
{
min=lowcost[j];
k=j;
}
printf("(%c,%c)--%d\n",g->vexs[closest[k]],g->vexs[k],lowcost[k]); /*输出该边*/
lowcost[k]=0; /*顶点k纳入最小生成树 */
for(j=0;j<g->vexnum;j++) /*求其他顶点到顶点k 的权*/
if(g->arcs[k][j]!=0&&g->arcs[k][j]<lowcost[j])
{
lowcost[j]=g->arcs[k][j];
closest[j]=k;
}
}
}
void printPath(graph g,int startVex,int EndVex)
{
int path[N][N],stack[N],top=0; /*堆栈*/
int i,k,j;
int flag[N]; /*输出路径顶点标志*/
k=EndVex;
for (i=0;i<g.vexnum;i++) flag[i]=0;
j=startVex;
printf("%c",g.vexs[j]);
flag[j]=1;
stack[top++]=k;
while (top>0) /*找j到k的路径*/
{
for (i=0;i<g.vexnum;i++)
{
if (path[k][i]==1 && flag[i]==0) /*j到k的路径含有i顶点*/
{
if (g.arcs[j][i]!=INF ) /*j到i的路径含有中间顶点*/
{
printf("-> %c(%d) ",g.vexs[i],g.arcs[j][i]);
/*输出j到k的路径的顶点i*/
flag[i]=1;
j=i;
k=stack[--top];
break;
}
else
{
if (i!=k) stack[top++]=i; /*break;*/
}
}
}
}
}
void dijkstra(graph g,int v){ /*dijkstra算法求单源最短路径*/
int path[N][N],dist[N],s[N];
int mindis,i,j,u,k;
for(i=0;i<g.vexnum;i++){
dist[i]=g.arcs[v][i];
s[i]=0;
for(j=0;j<g.vexnum;j++)
path[i][j]=0;
if(dist[i]<INF){
path[i][v]=1;
path[i][i]=1;
}
}
dist[v]=0;
s[v]=1;
for(i=0,u=1;i<g.vexnum;i++){
mindis=INFIN;
for(j=0;j<g.vexnum;j++)
if(s[j]==0)
if(dist[j]<mindis){
u=j;
mindis=dist[j];
}
s[u]=1;
for(j=0;j<g.vexnum;j++)
if((s[j]==0)&&dist[u]+g.arcs[u][j]<dist[j]){
dist[j]=dist[u]+g.arcs[u][j];
for(k=0;k<g.vexnum;k++)
path[j][k]=path[u][k];
path[j][j]=1;
}
}
printf("\n顶点%c->到各顶点的最短路径\n",g.vexs[v]);
for(i=0;i<g.vexnum;i++){
printf("\n顶点%c->顶点%c:",g.vexs[v],g.vexs[i]);
if(dist[i]==INF||dist[i]==0)
printf("无路径");
else{
printf("%d ",dist[i]);
printf("经过顶点:");
printPath(g,v,i); /*输出v到i的路径*/
}
}
}
void showprim()/*最小生成树prim算法演示*/
{
graph ga;
createGraph_w(&ga,1);
prim(&ga,0);
}
void showdij(){ /*dijstra算法演示*/
graph ga;
createGraph_w(&ga,0);
dijkstra(ga,0);
}
int main(){
showprim(); /*prim算法演示*/
getchar();
showdij(); /*dijstra算法演示*/
return 0;
}
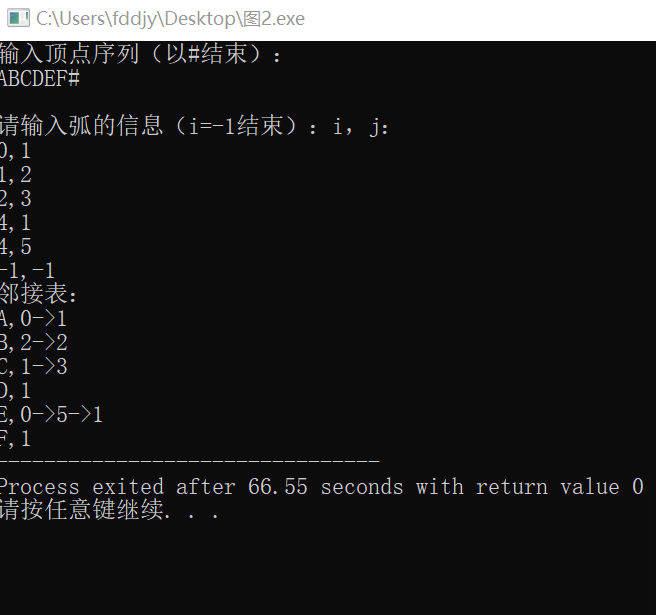
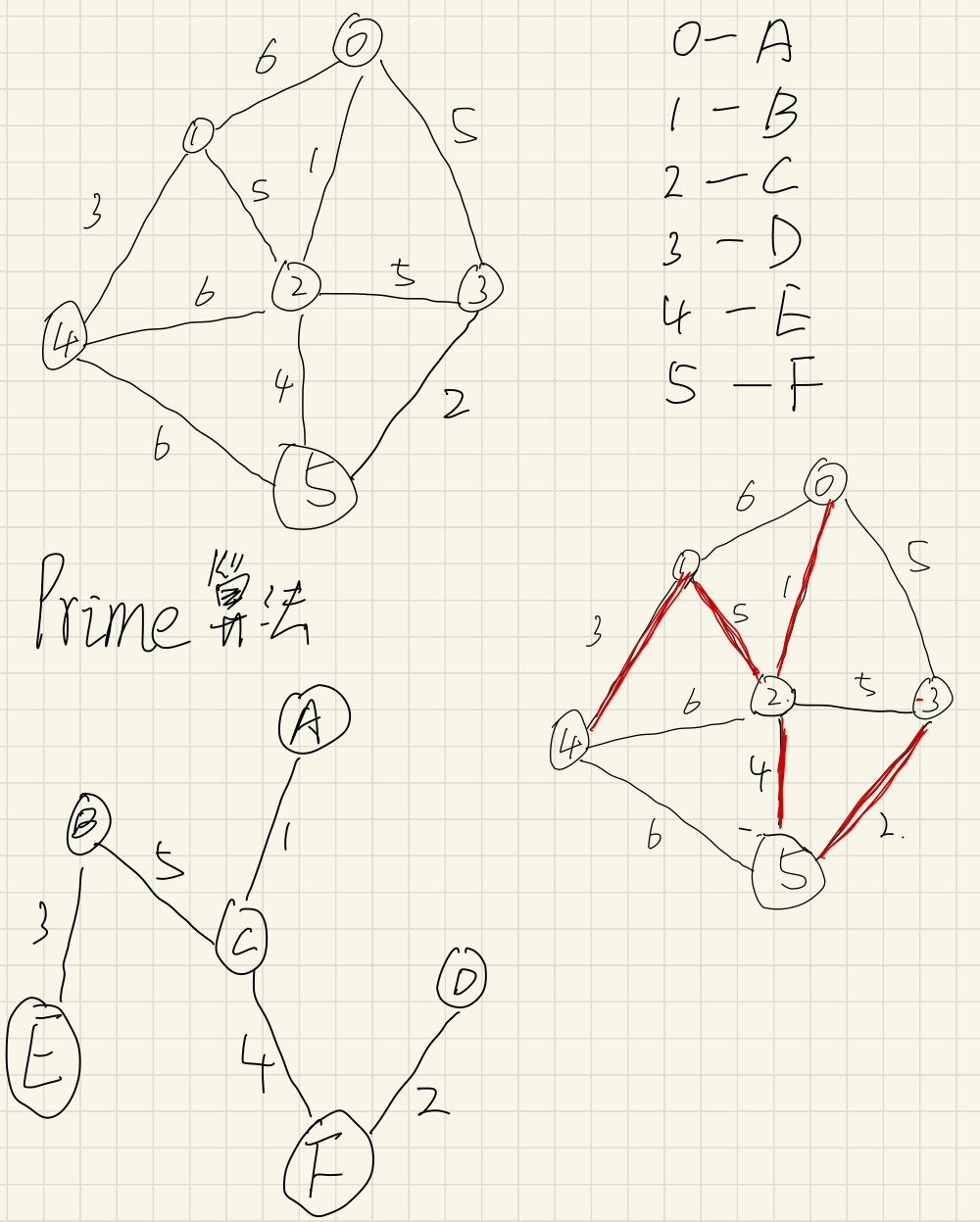
·下面的输入分别验证prim算法和dijstra算法。输入实例的第一部分为无向图,求其最小生成树;输入的第二部分为有向图,求其最短路径。
ABCDEF#
0,1,6
0,2,1
0,3,5
1,2,5
1,4,3
2,3,5
2,4,6
2,5,4
3,5,2
4,5,6
-1,-1,-1
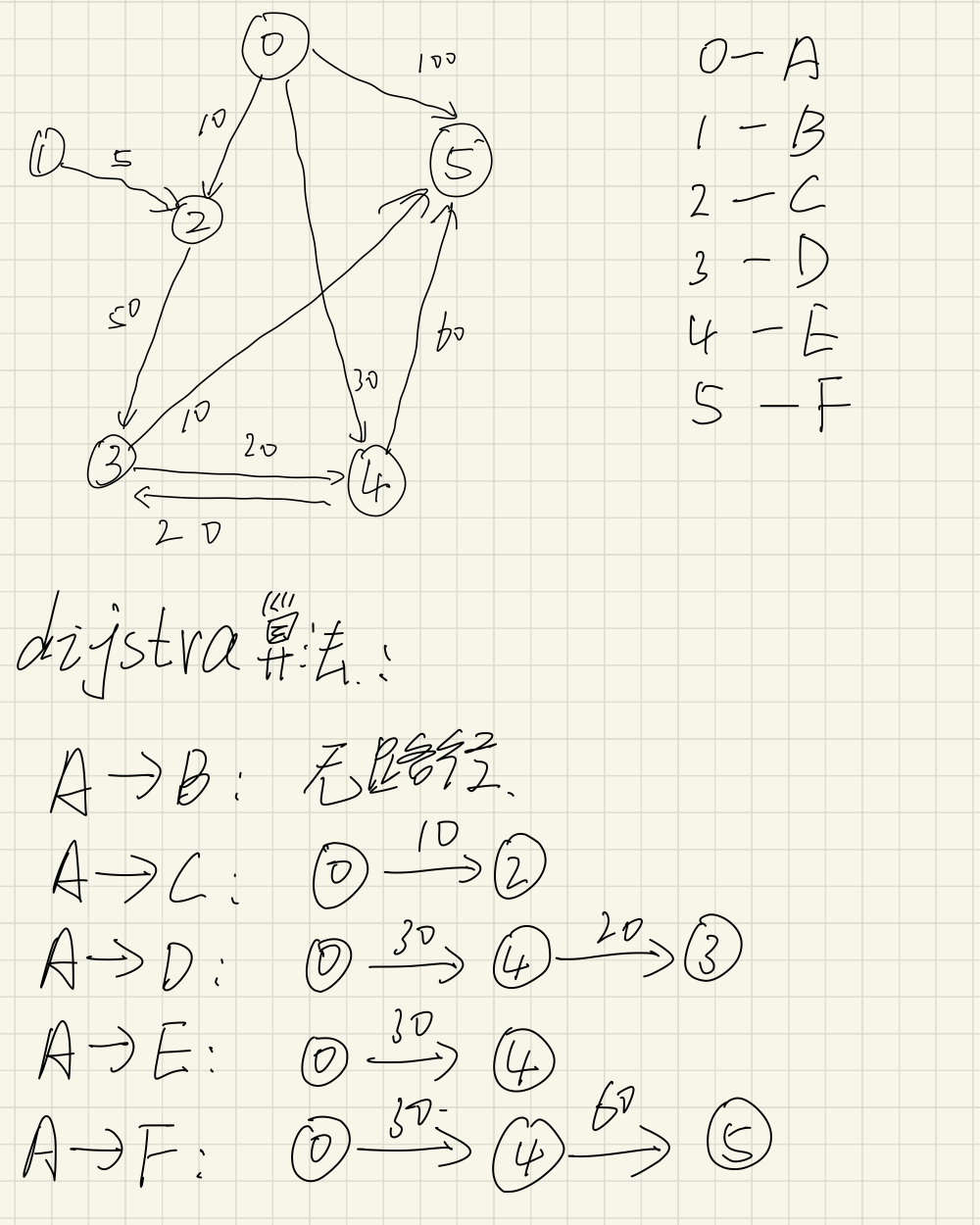
ABCDEF#
0,2,10
0,5,100
0,4,30
1,2,5
2,3,50
3,4,20
3,5,10
4,3,20
4,5,60
-1,-1,-1
·运行结果:(并画出两个图)
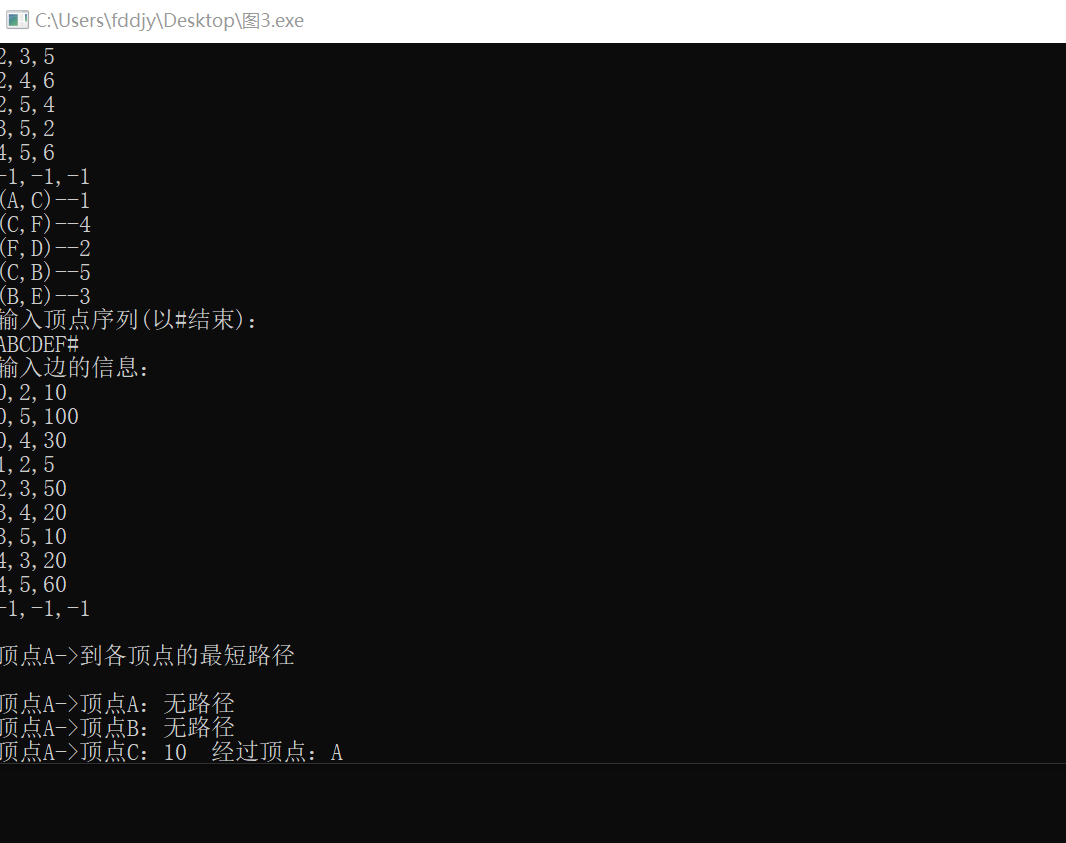
最小生成树
最短路径
四、实验小结
深度优先和广度优先搜索方法,对于带权有向图的最短路径、无向图的最小生成树



 浙公网安备 33010602011771号
浙公网安备 33010602011771号