[洛谷P3195][题解][HNOI2008]玩具装箱

0.？？？

呼_{总算是吧斜率优化这个磨人的小妖精攻下了呢}
今天经过老师讲解和洛咕题解的帮助感觉理解得更加透彻了。
所以就又来水题解啦~

1.题目

给出一个序列\(\{a_i\}\)（此处\(a_i\)为原题中\(C_i+1\)），试将其划分为若干段，使每一段的价值和

\[\sum_i(\sum_{j\in[l_i,r_i]} a_j-L)^2 \]

最小，并求出这个最小值。

2.题解 Part.1

状态和方程很简单，直接在此列出：
设\(f[i]\)为前\(i\)个玩具的最低价值和，则

\[f[i]=min\{f[j]+(sum[i]-sum[j]-1-L)^2\},j<i \]

，其中\(sum[i]\)代表玩具\(i\)的前缀和（包括长度为1的填充物）。
复杂度太高，肯定要优化，但是这个柿子拆开后变成了：

\[f[i]=f[j]+sum[i]^2+(sum[j]+L+1)^2-2sum[i](sum[j]+L+1) \]

出现了一个碍眼的\(2sum[i](sum[j]+L+1)\)，我们化不掉，于是顺势变个性形：

\[2sum[i](sum[j]+L+1)+f[i]-sum[i]^2=f[j]+(sum[j]+L+1)^2 \]

她变成了一条经过\((sum[j]+L+1,f[j]+(sum[j]+L+1)^2)\)且斜率为\(2sum[i]\)的直线。
回头看\(f[i]\)，我们发现答案正是这条直线的最小纵截距！
如图，有\(n\)个点，找一条斜率为\(2sum[i]\)的直线使其穿过某个点且纵截距最小：

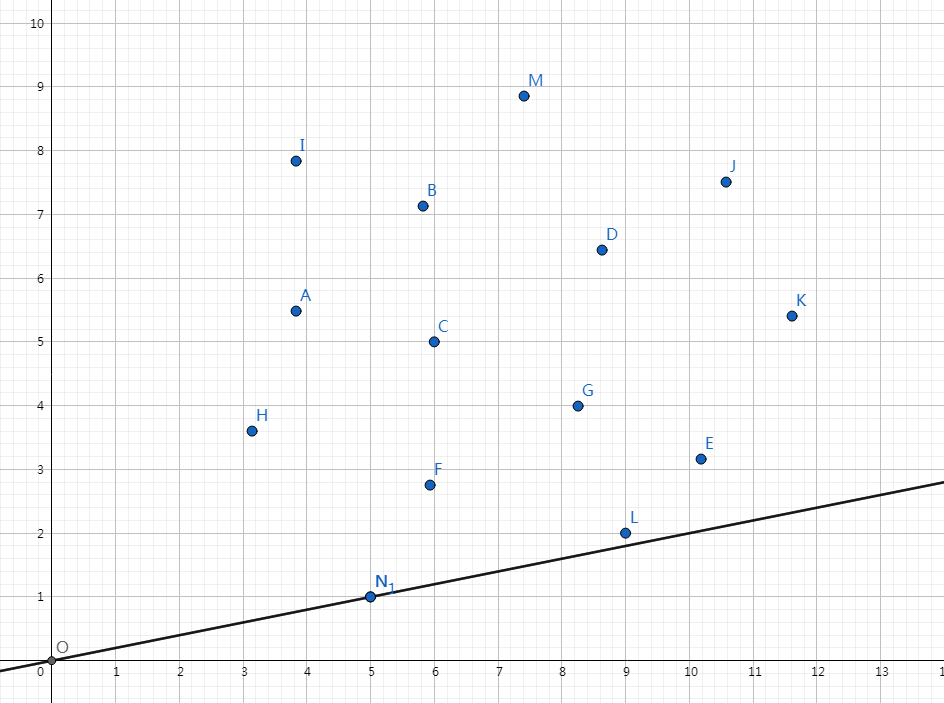
由图易知，满足条件的点一定组成一个下凸壳：

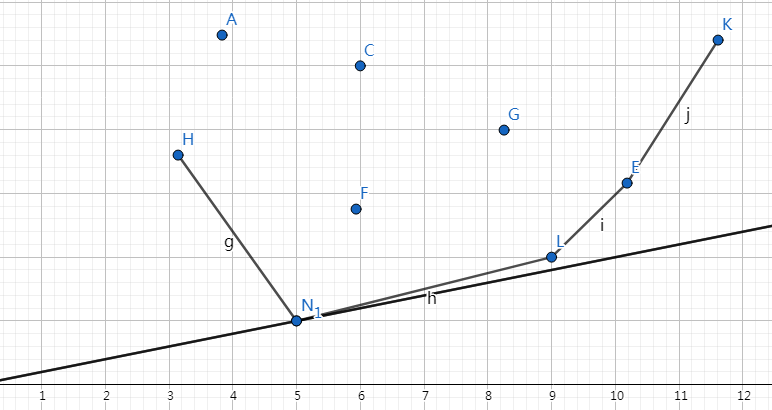
这时可以用单调队列来维护了。

3.题解 Part.2

那么单调队列怎么用呢？换言之，需要找到弹出队头队尾无用点的条件。
1.假设队头为\(q[hd]\)，则\(Slope(q[hd],q[hd+1])<2sum[i]\)时，弹出队头。
如图：

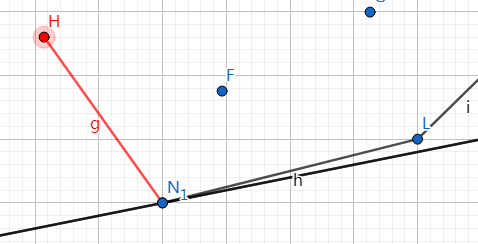
上面的\(H\)点在直线上移的过程中已经碰不到了对吧。
2.假设队尾为\(q[tl]\)，则\(Slope(q[tl-1],q[tl])>Slope(i,q[tl-1])\)时，弹出队尾。
如图：

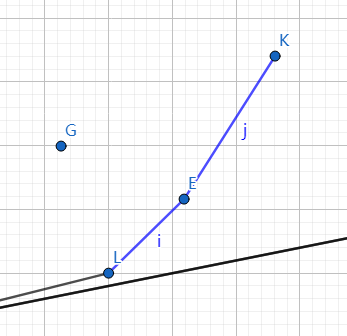
线段\(j\)的斜率比线段\(i\)大，这表明\(K\)已经没有机会了。（您看我还有机会吗）
然后每次都把当前点加进来维护就可以啦~

4.代码

#define N 50010
int n,L;
double c[N],f[N];
inline double Slope(int a,int b){
	double xa=c[a]+L+1,xb=c[b]+L+1;
	double ya=f[a]+(c[a]+L+1)*(c[a]+L+1);
	double yb=f[b]+(c[b]+L+1)*(c[b]+L+1);
	return (yb-ya)/(xb-xa);
}
signed main(){
	Read(n),Read(L);
	for(rg int i=1;i<=n;i++){
		cin>>c[i];
		c[i]+=c[i-1]+1;
	}
	int q[N],hd=1,tl=1;
	for(rg int i=1;i<=n;i++){
		while(hd<tl&&Slope(q[hd],q[hd+1])<2*c[i])hd++;
		f[i]=f[q[hd]]+(c[i]-c[q[hd]]-L-1)*(c[i]-c[q[hd]]-L-1);
		while(hd<tl&&Slope(i,q[tl-1])<Slope(q[tl-1],q[tl]))tl--;
		q[++tl]=i;
	}
	cout<<(int)f[n]<<endl;
	return 0;
}

此题勿忘开LL！！！！！！！！！！

5.说句闲话

研究斜率优化的最好方法是：其实今天老师还讲了个升维打击来着……
就是把一开始的DP柿子乘开后化为点乘的形式，就可以当做向量做了blabla
其实和洛咕题解的基本思想是一样的，只不过总感觉哪里有点怪异……？
之后有时间补一补这种做法吧（咕~）。