网络流基础知识

1.流函数
给定一个网络\(G=(V,E)\),每条边有一个c(x,y)
流函数满足:\(f(x,y)\):
\(f(x,y) \le c(x,y)\) 容量限制
\(f(x,y)=-f(y,x)\) 斜对称
\(\sum f(u,x)=\sum f(x,v)\) 流量守恒

2. EK
3. 增广路 存在路径S->T, 任意一条边剩余容量>0
   不断寻找增广路 更新当前边容量和反向边容量 知道不存在增广路
   反向边相当于反悔容量

3.Dinic
多路增广 每次选择发现流量没有用完后就再去增广 每次只在分层图上增广
即先考虑能直接到达T的边 再考虑层之间的边

int dinic(int x,int flow)
{
	if(x==T) return flow;
	int rest=flow;
	for(int i=head[x];i&&rest;i=e[i].next)//及时剪枝 
	{
		int y=e[i].to;
		if(e[i].w&&d[y]==d[x]+1)
		{
			int k=dinic(y,min(rest,e[i].w));
			if(!k) d[y]=0;
			e[i].w-=k; e[i^1].w+=k; rest-=k;
		}
	}
	return flow-rest;
}

为什么要判断e.w为0呢?
原因在于: k=0的时候代表着已经搜过 并且增广路不存在
而已经流满的边相连的点并不意味着不存在增广路
如果去掉的话 会存在反例:

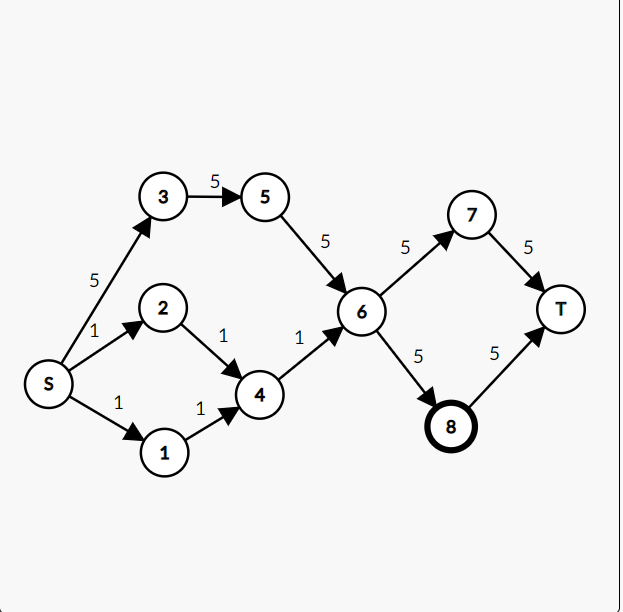
(输入时最后输入边2 4 1/1 4 1)

最小割=最大流
残量网络的点和其他点之间的边构成最小割

费用流
bfs找增广路改成用spfa找增广路